Koliki je logaritam jedne? Pretvaranje izraza korištenjem svojstava logaritama: primjeri, rješenja

Kao što znate, kada se množe izrazi sa stepenom, njihovi eksponenti se uvijek sabiraju (a b *a c = a b+c). Ovaj matematički zakon je izveo Arhimed, a kasnije, u 8. veku, matematičar Virasen je napravio tabelu celobrojnih eksponenata. Upravo su oni poslužili za dalje otkrivanje logaritama. Primjeri korištenja ove funkcije mogu se naći gotovo svugdje gdje je potrebno pojednostaviti glomazno množenje jednostavnim sabiranjem. Ako odvojite 10 minuta čitajući ovaj članak, objasnit ćemo vam šta su logaritmi i kako s njima raditi. Jednostavnim i pristupačnim jezikom.

Definicija u matematici

Logaritam je izraz sljedećeg oblika: log a b=c, to jest, logaritam bilo kojeg nenegativnog broja (tj. bilo kojeg pozitivnog) “b” na njegovu bazu “a” smatra se stepenom “c ” na koju se baza “a” mora podići da bi se na kraju dobila vrijednost “b”. Analizirajmo logaritam na primjerima, recimo da postoji izraz log 2 8. Kako pronaći odgovor? Vrlo je jednostavno, potrebno je pronaći takvu snagu da od 2 do tražene snage dobijete 8. Nakon nekih proračuna u glavi, dobijamo broj 3! I to je tačno, jer 2 na stepen od 3 daje odgovor kao 8.

Vrste logaritama

Mnogim studentima ova tema se čini komplikovanom i nerazumljivom, ali zapravo logaritmi nisu toliko strašni, najvažnije je razumjeti njihovo općenito značenje i zapamtiti njihova svojstva i neka pravila. Postoje tri odvojene vrste logaritamskih izraza:

1. Prirodni logaritam ln a, gdje je baza Ojlerov broj (e = 2,7).
2. Decimala a, gdje je osnova 10.
3. Logaritam bilo kojeg broja b na osnovu a>1.

Svaki od njih se rješava na standardni način, uključujući pojednostavljenje, redukciju i naknadno svođenje na jedan logaritam korištenjem logaritamskih teorema. Da biste dobili ispravne vrijednosti logaritama, trebali biste zapamtiti njihova svojstva i redoslijed radnji prilikom njihovog rješavanja.

Pravila i neka ograničenja

U matematici postoji nekoliko pravila-ograničenja koja su prihvaćena kao aksiom, odnosno nisu predmet rasprave i predstavljaju istinu. Na primjer, nemoguće je podijeliti brojeve sa nulom, a također je nemoguće izdvojiti paran korijen negativnih brojeva. Logaritmi također imaju svoja pravila, slijedeći koja možete lako naučiti raditi čak i sa dugim i prostranim logaritamskim izrazima:

• Osnova “a” uvijek mora biti veća od nule, a ne jednaka 1, inače će izraz izgubiti svoje značenje, jer su “1” i “0” u bilo kom stepenu uvijek jednaki njihovim vrijednostima;
• ako je a > 0, onda a b > 0, ispada da “c” takođe mora biti veće od nule.

Kako riješiti logaritme?

Na primjer, daje se zadatak pronaći odgovor na jednadžbu 10 x = 100. Ovo je vrlo lako, potrebno je odabrati stepen podizanjem broja deset na koji dobijamo 100. Ovo je, naravno, 10 2 = 100.

Sada predstavimo ovaj izraz u logaritamskom obliku. Dobijamo log 10 100 = 2. Prilikom rješavanja logaritma, sve radnje se praktično konvergiraju da bi se pronašla potencija na koju je potrebno unijeti bazu logaritma da bi se dobio dati broj.

Da biste precizno odredili vrijednost nepoznatog stepena, morate naučiti kako raditi s tablicom stupnjeva. izgleda ovako:

Kao što vidite, neki eksponenti se mogu pogoditi intuitivno ako imate tehnički um i poznavanje tablice množenja. Međutim, za veće vrijednosti trebat će vam stol za napajanje. Mogu ga koristiti čak i oni koji ne znaju ništa o složenim matematičkim temama. Lijeva kolona sadrži brojeve (osnova a), gornji red brojeva je vrijednost stepena c na koji je broj a podignut. Na raskrsnici ćelije sadrže brojčane vrijednosti koje su odgovor (a c =b). Uzmimo, na primjer, prvu ćeliju sa brojem 10 i kvadriramo je, dobićemo vrijednost 100, koja je naznačena na sjecištu naše dvije ćelije. Sve je tako jednostavno i lako da će i najistinskiji humanista razumjeti!

Jednačine i nejednačine

Ispada da je pod određenim uslovima eksponent logaritam. Stoga se bilo koji matematički numerički izrazi može zapisati kao logaritamska jednakost. Na primjer, 3 4 =81 se može napisati kao logaritam 81 na bazi 3 jednak četiri (log 3 81 = 4). Za negativne potencije pravila su ista: 2 -5 = 1/32 zapišemo to kao logaritam, dobijemo log 2 (1/32) = -5. Jedna od najfascinantnijih sekcija matematike je tema "logaritma". U nastavku ćemo pogledati primjere i rješenja jednadžbi, odmah nakon proučavanja njihovih svojstava. Pogledajmo sada kako izgledaju nejednakosti i kako ih razlikovati od jednačina.

Dat je sljedeći izraz: log 2 (x-1) > 3 - to je logaritamska nejednakost, jer je nepoznata vrijednost “x” ispod logaritamskog predznaka. I također se u izrazu upoređuju dvije veličine: logaritam željenog broja na osnovu dva je veći od broja tri.

Najvažnija razlika između logaritamskih jednadžbi i nejednačina je u tome što jednadžbe sa logaritmima (na primjer, logaritam 2 x = √9) podrazumijevaju jednu ili više specifičnih brojčanih vrijednosti u odgovoru, dok se pri rješavanju nejednadžbe uzimaju i raspon prihvatljivih vrijednosti ​​i tačke se određuju kršenjem ove funkcije. Kao posljedica toga, odgovor nije jednostavan skup pojedinačnih brojeva, kao u odgovoru na jednadžbu, već kontinuirani niz ili skup brojeva.

Osnovne teoreme o logaritmima

Prilikom rješavanja primitivnih zadataka pronalaženja vrijednosti logaritma, njegova svojstva možda neće biti poznata. Međutim, kada su u pitanju logaritamske jednačine ili nejednačine, prije svega je potrebno jasno razumjeti i primijeniti u praksi sva osnovna svojstva logaritama. Kasnije ćemo pogledati primjere jednačina;

1. Glavni identitet izgleda ovako: a logaB =B. Primjenjuje se samo kada je a veće od 0, nije jednako jedan, a B je veće od nule.
2. Logaritam proizvoda se može predstaviti sljedećom formulom: log d (s 1 * s 2) = log d s 1 + log d s 2. U ovom slučaju, obavezan uslov je: d, s 1 i s 2 > 0; a≠1. Možete dati dokaz za ovu logaritamsku formulu, sa primjerima i rješenjem. Neka log a s 1 = f 1 i log a s 2 = f 2, tada a f1 = s 1, a f2 = s 2. Dobijamo da je s 1 * s 2 = a f1 *a f2 = a f1+f2 (osobine stepeni ), a zatim po definiciji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, što je trebalo dokazati.
3. Logaritam količnika izgleda ovako: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Teorema u obliku formule ima sljedeći oblik: log a q b n = n/q log a b.

Ova formula se naziva “svojstvo stepena logaritma”. Podsjeća na svojstva običnih stupnjeva, i nije iznenađujuće, jer se sva matematika zasniva na prirodnim postulatima. Pogledajmo dokaz.

Neka log a b = t, ispada da je a t = b. Ako oba dijela podignemo na stepen m: a tn = b n ;

ali pošto je a tn = (a q) nt/q = b n, dakle log a q b n = (n*t)/t, onda log a q b n = n/q log a b. Teorema je dokazana.

Primjeri problema i nejednakosti

Najčešći tipovi zadataka o logaritmima su primjeri jednačina i nejednačina. Nalaze se u gotovo svim knjigama zadataka, a također su obavezan dio ispita iz matematike. Da biste ušli na fakultet ili položili prijemne ispite iz matematike, morate znati kako pravilno riješiti takve zadatke.

Nažalost, ne postoji jedinstveni plan ili shema za rješavanje i određivanje nepoznate vrijednosti logaritma, ali se određena pravila mogu primijeniti na svaku matematičku nejednakost ili logaritamsku jednačinu. Prije svega, trebali biste saznati da li se izraz može pojednostaviti ili svesti na opći oblik. Duge logaritamske izraze možete pojednostaviti ako pravilno koristite njihova svojstva. Hajde da ih brzo upoznamo.

Prilikom rješavanja logaritamskih jednadžbi moramo odrediti koji tip logaritma imamo: primjer izraza može sadržavati prirodni logaritam ili decimalni.

Evo primjera ln100, ln1026. Njihovo rješenje se svodi na činjenicu da treba odrediti snagu kojoj će baza 10 biti jednaka 100 i 1026, respektivno. Da biste riješili prirodne logaritme, morate primijeniti logaritamske identitete ili njihova svojstva. Pogledajmo primjere rješavanja logaritamskih problema različitih tipova.

Kako koristiti logaritamske formule: s primjerima i rješenjima

Dakle, pogledajmo primjere korištenja osnovnih teorema o logaritmima.

1. Svojstvo logaritma proizvoda može se koristiti u zadacima gdje je potrebno rastaviti veliku vrijednost broja b na jednostavnije faktore. Na primjer, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odgovor je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kao što vidite, koristeći četvrto svojstvo stepena logaritma, uspjeli smo riješiti naizgled složen i nerješiv izraz. Vi samo trebate faktorisati bazu, a zatim izvući vrijednosti eksponenta iz predznaka logaritma.

Zadaci sa Jedinstvenog državnog ispita

Logaritmi se često nalaze na prijemnim ispitima, posebno mnogi logaritamski problemi na Jedinstvenom državnom ispitu (državni ispit za sve maturante). Obično su ovi zadaci prisutni ne samo u dijelu A (najlakši dio ispita), već i u dijelu C (najsloženiji i najobimniji zadaci). Ispit zahtijeva tačno i savršeno poznavanje teme „Prirodni logaritmi“.

Primjeri i rješenja problema preuzeti su iz službenih verzija Jedinstvenog državnog ispita. Pogledajmo kako se takvi zadaci rješavaju.

Dat log 2 (2x-1) = 4. Rješenje:
prepišimo izraz, pojednostavljujući ga malo log 2 (2x-1) = 2 2, po definiciji logaritma dobijamo da je 2x-1 = 2 4, dakle 2x = 17; x = 8,5.

• Najbolje je sve logaritme svesti na istu bazu kako rješenje ne bi bilo glomazno i ​​zbunjujuće.
• Svi izrazi pod predznakom logaritma su označeni kao pozitivni, stoga, kada se eksponent izraza koji je pod predznakom logaritma i kao njegova baza izvadi kao množitelj, izraz koji ostaje pod logaritmom mora biti pozitivan.

Danas ćemo razgovarati o logaritamske formule a mi ćemo dati indikativno primjeri rješenja.

Oni sami po sebi podrazumijevaju obrasce rješenja prema osnovnim svojstvima logaritama. Prije primjene logaritamskih formula za rješavanje, podsjetimo vas na sva svojstva:

Sada ćemo na osnovu ovih formula (osobina) pokazati primjeri rješavanja logaritama.

Primjeri rješavanja logaritama na osnovu formula.

Logaritam pozitivan broj b na bazi a (označen log a b) je eksponent na koji se a mora podići da bi se dobilo b, sa b > 0, a > 0 i 1.

Prema definiciji, log a b = x, što je ekvivalentno a x = b, dakle log a a x = x.

Logaritmi, primjeri:

log 2 8 = 3, jer 2 3 = 8

log 7 49 = 2, jer 7 2 = 49

log 5 1/5 = -1, jer 5 -1 = 1/5

Decimalni logaritam- ovo je običan logaritam čija je baza 10. Označava se kao lg.

log 10 100 = 2, jer 10 2 = 100

Prirodni logaritam- takođe običan logaritam, logaritam, ali sa osnovom e (e = 2,71828... - iracionalan broj). Označeno kao ln.

Preporučljivo je zapamtiti formule ili svojstva logaritama, jer će nam kasnije trebati pri rješavanju logaritama, logaritamskih jednadžbi i nejednačina. Proradimo ponovo kroz svaku formulu s primjerima.

• Osnovni logaritamski identitet
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Logaritam proizvoda jednak je zbroju logaritama
  log a (bc) = log a b + log a c

  log 3 8.1 + log 3 10 = log 3 (8.1*10) = log 3 81 = 4

• Logaritam količnika jednak je razlici logaritama
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Svojstva stepena logaritamskog broja i baze logaritma

  Eksponent logaritamskog broja log a b m = mlog a b

  Eksponent baze logaritma log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  ako je m = n, dobijamo log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Prelazak na novu osnovu
  log a b = log c b/log c a,

  ako je c = b, dobijamo log b b = 1

  tada je log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Kao što vidite, formule za logaritme nisu tako komplikovane kao što se čine. Sada, nakon što smo pogledali primjere rješavanja logaritama, možemo prijeći na logaritamske jednadžbe. Detaljnije ćemo pogledati primjere rješavanja logaritamskih jednadžbi u članku: "". Ne propustite!

Ako i dalje imate pitanja o rješenju, napišite ih u komentarima na članak.

Napomena: odlučili smo da dobijemo drugu klasu obrazovanja i studiramo u inostranstvu kao opciju.

Logaritam broja N na osnovu A naziva eksponent X , do koje trebate izgraditi A da dobijem broj N

Pod uslovom da
,
,

Iz definicije logaritma slijedi da
, tj.
- ova jednakost je osnovni logaritamski identitet.

Logaritmi na osnovu 10 nazivaju se decimalni logaritmi. Umjesto
pisati
.

Logaritmi bazi e nazivaju se prirodnim i označavaju se
.

Osnovna svojstva logaritama.

Logaritam od jedan je jednak nuli za bilo koju bazu.

Logaritam proizvoda jednak je zbiru logaritama faktora.

3) Logaritam količnika jednak je razlici logaritama

Faktor
nazivamo modulom prijelaza sa logaritama na bazu a na logaritme u osnovi b .

Koristeći svojstva 2-5, često je moguće svesti logaritam složenog izraza na rezultat jednostavnih aritmetičkih operacija nad logaritmima.

Na primjer,

Takve transformacije logaritma nazivaju se logaritmi. Transformacije inverzne logaritmima nazivaju se potenciranje.

Poglavlje 2. Elementi više matematike.

1. Ograničenja

Granica funkcije
je konačan broj A ako je kao xx 0 za svaku unapred određenu
, postoji takav broj
da čim
, To
.

Funkcija koja ima ograničenje razlikuje se od nje za beskonačno mali iznos:
, gdje je- b.m.v., tj.
.

Primjer. Razmotrite funkciju
.

Kada težite
, funkcija y teži nuli:

1.1. Osnovne teoreme o granicama.

Granica konstantne vrijednosti jednaka je ovoj konstantnoj vrijednosti

.

Granica zbira (razlike) konačnog broja funkcija jednaka je zbiru (razlici) granica ovih funkcija.

Granica proizvoda konačnog broja funkcija jednaka je proizvodu granica ovih funkcija.

Granica kvocijenta dvije funkcije jednaka je količniku granica ovih funkcija ako granica nazivnika nije nula.

Wonderful Limits

,
, Gdje

1.2. Primjeri izračuna ograničenja

Međutim, nisu sve granice izračunate tako lako. Češće se izračunavanje granice svodi na otkrivanje nesigurnosti tipa: ili .

.

2. Derivat funkcije

Hajde da imamo funkciju
, kontinuirano na segmentu
.

Argument dobio neko povećanje
. Tada će funkcija dobiti povećanje
.

Vrijednost argumenta odgovara vrijednosti funkcije
.

Vrijednost argumenta
odgovara vrijednosti funkcije.

Dakle, .

Nađimo granicu ovog omjera na
. Ako ova granica postoji, onda se naziva derivacijom date funkcije.

Definicija 3 Derivat date funkcije
argumentom naziva se granica omjera prirasta funkcije i priraštaja argumenta, kada inkrement argumenta proizvoljno teži nuli.

Derivat funkcije
može se označiti na sljedeći način:

; ; ; .

Definicija 4 Operacija pronalaženja derivacije funkcije se zove diferencijaciju.

2.1. Mehaničko značenje izvedenice.

Razmotrimo pravolinijsko kretanje nekog krutog tijela ili materijalne tačke.

Neka u nekom trenutku pokretna tačka
bio na distanci sa početne pozicije
.

Nakon nekog vremena
odmakla se
. Stav =- prosječna brzina materijalne tačke
. Nađimo granicu ovog omjera, uzimajući to u obzir
.

Posljedično, određivanje trenutne brzine kretanja materijalne točke svodi se na pronalaženje derivacije putanje u odnosu na vrijeme.

2.2. Geometrijska vrijednost derivacije

Hajde da imamo grafički definisanu funkciju
.

Rice. 1. Geometrijsko značenje izvoda

Ako
, zatim pokažite
, će se kretati duž krive, približavajući se tački
.

Dakle
, tj. vrijednost izvoda za datu vrijednost argumenta numerički jednak tangentu ugla koji formira tangenta u datoj tački sa pozitivnim smerom ose
.

2.3. Tabela osnovnih formula diferencijacije.

Funkcija napajanja

Eksponencijalna funkcija

Logaritamska funkcija

Trigonometrijska funkcija

Inverzna trigonometrijska funkcija

2.4. Pravila diferencijacije.

Derivat od

Derivat zbira (razlike) funkcija

Derivat proizvoda dvije funkcije

Derivat kvocijenta dvije funkcije

2.5. Derivat kompleksne funkcije.

Neka je funkcija data
tako da se može predstaviti u obliku

I
, gdje je varijabla onda je srednji argument

Derivat kompleksne funkcije jednak je umnošku izvoda date funkcije u odnosu na međuargument i derivacije srednjeg argumenta u odnosu na x.

Primjer 1.

Primjer 2.

3. Diferencijalna funkcija.

Neka bude
, diferencibilan na nekom intervalu
pusti to at ova funkcija ima izvod

,

onda možemo pisati

(1),

Gdje - beskonačno mala količina,

od kada

Množenje svih pojmova jednakosti (1) sa
imamo:

Gdje
- b.m.v. višeg reda.

Magnituda
naziva se diferencijalom funkcije
i određen je

.

3.1. Geometrijska vrijednost diferencijala.

Neka je funkcija data
.

Fig.2. Geometrijsko značenje diferencijala.

.

Očigledno, diferencijal funkcije
jednak je inkrementu ordinate tangente u datoj tački.

3.2. Derivati ​​i diferencijali različitih redova.

Ako tamo
, Onda
naziva se prvim izvodom.

Izvod prvog izvoda naziva se izvod drugog reda i piše se
.

Derivat n-tog reda funkcije
naziva se derivat (n-1)-tog reda i piše se:

.

Diferencijal diferencijala funkcije naziva se drugi diferencijal ili diferencijal drugog reda.

.

.

3.3 Rješavanje bioloških problema pomoću diferencijacije.

Zadatak 1. Istraživanja su pokazala da je rast kolonije mikroorganizama u skladu sa zakonom
, Gdje N – broj mikroorganizama (u hiljadama), t – vrijeme (dani).

b) Hoće li se populacija kolonije povećati ili smanjiti tokom ovog perioda?

Odgovori. Veličina kolonije će se povećati.

Zadatak 2. Voda u jezeru se periodično testira radi praćenja sadržaja patogenih bakterija. Kroz t dana nakon testiranja, koncentracija bakterija se određuje omjerom

.

Kada će jezero imati minimalnu koncentraciju bakterija i hoće li se u njemu moći kupati?

Rješenje: Funkcija dostiže maksimum ili min kada je njen izvod nula.

,

Odredimo max ili min će biti za 6 dana. Da bismo to učinili, uzmimo drugi izvod.

Odgovor: Nakon 6 dana bit će minimalna koncentracija bakterija.

Raspon prihvatljivih vrijednosti (APV) logaritma

Sada razgovarajmo o ograničenjima (ODZ - raspon dozvoljenih vrijednosti varijabli).

Sjećamo se da se, na primjer, kvadratni korijen ne može uzeti iz negativnih brojeva; ili ako imamo razlomak, onda imenilac ne može biti jednak nuli. Logaritmi imaju slična ograničenja:

To jest, i argument i baza moraju biti veći od nule, ali baza još uvijek ne može biti jednaka.

Žašto je to?

Počnimo s jednostavnom stvari: recimo to. Tada, na primjer, broj ne postoji, jer bez obzira na koju snagu dižemo, uvijek ispadne. Štaviše, ne postoji ni za koga. Ali u isto vrijeme može biti jednako bilo čemu (iz istog razloga - jednako bilo kojem stepenu). Dakle, predmet nije od interesa, i jednostavno je izbačen iz matematike.

Imamo sličan problem u slučaju: na bilo koju pozitivnu potenciju jeste, ali se nikako ne može podići na negativnu, jer će to rezultirati podjelom sa nulom (da vas podsjetim).

Kada smo suočeni s problemom podizanja na razlomak (koji je predstavljen kao korijen: . Na primjer, (to jest), ali on ne postoji.

Stoga je lakše odbaciti negativne razloge nego petljati s njima.

Pa, pošto naša baza a može biti samo pozitivna, onda bez obzira na to na koju je potenciju podignemo, uvijek ćemo dobiti striktno pozitivan broj. Dakle, argument mora biti pozitivan. Na primjer, ne postoji, jer neće biti negativan broj ni u kom stepenu (pa čak ni nula, stoga ni ne postoji).

Kod problema s logaritmima, prvo što trebate učiniti je zapisati ODZ. Dozvolite mi da vam dam primjer:

Hajde da riješimo jednačinu.

Prisjetimo se definicije: logaritam je snaga na koju se baza mora podići da bi se dobio argument. A prema uslovu, ovaj stepen je jednak: .

Dobijamo uobičajenu kvadratnu jednačinu: . Rešimo ga koristeći Vietin teorem: zbir korijena je jednak, a proizvod. Lako se podiže, ovo su brojevi i.

Ali ako odmah uzmete i upišete oba ova broja u odgovor, možete dobiti 0 bodova za zadatak. Zašto? Hajde da razmislimo o tome šta se dešava ako ove korene zamenimo u početnu jednačinu?

Ovo je očigledno netačno, jer baza ne može biti negativna, odnosno korijen je „treća strana“.

Da biste izbjegli takve neugodne zamke, morate zapisati ODZ čak i prije nego počnete rješavati jednadžbu:

Zatim, primivši korijene i, odmah odbacimo korijen i napišemo tačan odgovor.

Primjer 1(pokušaj to sam riješiti) :

Pronađite korijen jednačine. Ako postoji nekoliko korijena, navedite najmanji od njih u svom odgovoru.

Rješenje:

Prije svega, napišimo ODZ:

Sada se prisjetimo šta je logaritam: na koji stepen trebate podići bazu da biste dobili argument? Do drugog. To je:

Čini se da je manji korijen jednak. Ali to nije tako: prema ODZ-u, korijen je strani, odnosno uopće nije korijen ove jednadžbe. Dakle, jednadžba ima samo jedan korijen: .

odgovor: .

Osnovni logaritamski identitet

Prisjetimo se definicije logaritma u općem obliku:

Zamijenimo logaritam u drugu jednakost:

Ova jednakost se zove osnovni logaritamski identitet. Iako je u suštini ovo jednakost - samo drugačije napisano definicija logaritma:

Ovo je moć do koje se morate podići da biste došli.

Na primjer:

Riješite sljedeće primjere:

Primjer 2.

Pronađite značenje izraza.

Rješenje:

Prisjetimo se pravila iz odjeljka: to jest, kada se stepen diže na stepen, eksponenti se množe. Primijenimo ga:

Primjer 3.

Dokaži to.

Rješenje:

Svojstva logaritama

Nažalost, zadaci nisu uvijek tako jednostavni - često je potrebno prvo pojednostaviti izraz, dovesti ga u uobičajeni oblik, pa će tek tada biti moguće izračunati vrijednost. Ovo je najlakše uraditi ako znate svojstva logaritama. Pa hajde da naučimo osnovna svojstva logaritama. Dokazat ću svaki od njih, jer je svako pravilo lakše zapamtiti ako znate odakle dolazi.

Sva ova svojstva moraju se zapamtiti bez njih, većina problema s logaritmima se ne može riješiti.

A sada o svim svojstvima logaritama detaljnije.

Nekretnina 1:

dokaz:

Neka bude onda.

Imamo: , itd.

Svojstvo 2: Zbir logaritama

Zbir logaritama sa istim bazama jednak je logaritmu proizvoda: .

dokaz:

Neka bude onda. Neka bude onda.

primjer: Pronađite značenje izraza: .

Rješenje: .

Formula koju ste upravo naučili pomaže da se pojednostavi zbir logaritama, a ne razlika, tako da se ovi logaritmi ne mogu odmah kombinirati. Ali možete učiniti suprotno - "podijelite" prvi logaritam na dva: A evo obećanog pojednostavljenja:
.
Zašto je ovo potrebno? Pa, na primjer: čemu je to jednako?

Sada je to očigledno.

Sad pojednostavite sami:

Zadaci:

odgovori:

Svojstvo 3: Razlika logaritama:

dokaz:

Sve je potpuno isto kao u tački 2:

Neka bude onda.

Neka bude onda. Imamo:

Primjer iz prethodnog paragrafa sada postaje još jednostavniji:

Složeniji primjer: . Možete li sami smisliti kako to riješiti?

Ovdje treba napomenuti da nemamo jedinstvenu formulu o logaritmima na kvadrat. Ovo je nešto slično izrazu - ne može se odmah pojednostaviti.

Stoga, hajde da se odmorimo od formula o logaritmima i razmislimo kakve formule najčešće koristimo u matematici? Od 7. razreda!

Ovo - . Morate se naviknuti na činjenicu da su posvuda! Javljaju se u eksponencijalnim, trigonometrijskim i iracionalnim problemima. Stoga ih se mora zapamtiti.

Ako pažljivo pogledate prva dva pojma, postaje jasno da je ovo razlika kvadrata:

Odgovor na provjeru:

Pojednostavite sami.

Primjeri

Odgovori.

Svojstvo 4: Izuzimanje eksponenta iz argumenta logaritma:

dokaz: I ovdje također koristimo definiciju logaritma: neka, onda. Imamo: , itd.

Ovo pravilo se može shvatiti na sljedeći način:

To jest, stepen argumenta se pomera ispred logaritma kao koeficijent.

primjer: Pronađite značenje izraza.

Rješenje: .

Odlučite sami:

primjeri:

odgovori:

Svojstvo 5: Uzimanje eksponenta iz baze logaritma:

dokaz: Neka bude onda.

Imamo: , itd.
Zapamtite: od osnove stepen se izražava kao suprotno broj, za razliku od prethodnog slučaja!

Svojstvo 6: Uklanjanje eksponenta iz baze i argumenta logaritma:

Ili ako su stepeni isti: .

Svojstvo 7: Prelazak na novu bazu:

dokaz: Neka bude onda.

Imamo: , itd.

Svojstvo 8: Zamijenite bazu i argument logaritma:

dokaz: Ovo je poseban slučaj formule 7: ako zamijenimo, dobijamo: , itd.

Pogledajmo još nekoliko primjera.

Primjer 4.

Pronađite značenje izraza.

Koristimo svojstvo logaritama br. 2 - zbir logaritama sa istom osnovom jednak je logaritmu proizvoda:

Primjer 5.

Pronađite značenje izraza.

Rješenje:

Koristimo svojstvo logaritma br. 3 i br. 4:

Primjer 6.

Pronađite značenje izraza.

Rješenje:

Koristimo svojstvo br. 7 - prijeđimo na bazu 2:

Primjer 7.

Pronađite značenje izraza.

Rješenje:

Kako vam se sviđa članak?

Ako čitate ove redove, onda ste pročitali cijeli članak.

I to je super!

Sada nam recite kako vam se sviđa članak?

Jeste li naučili rješavati logaritme? Ako ne, u čemu je problem?

Pišite nam u komentarima ispod.

I, da, sretno na ispitima.

Na Jedinstvenom državnom ispitu i Jedinstvenom državnom ispitu i uopšte u životu

Logaritam pozitivan broj N do baze(b> 0, b 1 ) naziva eksponent x , do koje trebate izgraditi b da dobijete N .

Logaritamski zapis:

Ovaj unos je ekvivalentan sljedećem:b x = N .

PRIMJERI: dnevnik 3 81 = 4, jer je 3 4 = 81;

Dnevnik 1/3 27 = – 3, budući da je (1/3) - 3 = 3 3 = 27.

Gornja definicija logaritma može se napisati kao identitet:

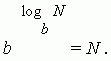
Osnovna svojstva logaritama.

1) log b= 1 , jer b 1 = b.

b

2) log 1 = 0 , jer b 0 = 1 .

b

3) Logaritam proizvoda jednak je zbroju logaritama faktora:

dnevnik( ab) = log a+ log b.

4) Logaritam kvocijenta jednak je razlici između logaritama dividende i djelitelja:

dnevnik( a/b) = log a–log b.

5) Logaritam stepena jednak je umnošku eksponenta i logaritma njegove baze:

log (b k ) = k log b.

Posljedica ovog svojstva je sljedeća:logaritam korijena jednak logaritmu radikalnog broja podijeljenog potencijom korijena:

6) Ako je osnova logaritma stepen, onda je vrijednost inverzno od eksponenta, može se izvaditi iz log znaka rima:

Posljednja dva svojstva mogu se kombinirati u jednu:

7) Formula prelaznog modula (tj. e . prelazak sa jedne bazelogaritam na drugu bazu):

U posebnom slučaju kada N=a imamo:

Decimalni logaritam pozvao osnovni logaritam 10. Određeno je lg, tj. dnevnik 10 N = lg N. Logaritmi brojeva 10, 100, 1000, ... str brojevi su 1, 2, 3, …, redomone.

imaju toliko pozitivnih jedinica, koliko nula ima u logaritamskom broju nakon jedan. Logaritmi brojeva 0,1, 0,01, 0,001, ... str –2, –3, …, tj. ima onoliko negativnih koliko ima nula ispred jedan u logaritamskom broju ( brojanje i nula cijelih brojeva). Logaritmi ostali brojevi imaju razlomak koji se zove mantissa. Cijelidio logaritma se zove karakteristika. Za praktičnu upotrebuNajprikladniji su decimalni logaritmi.

Prirodni logaritam pozvao osnovni logaritam e. Određeno je ln, tj. log eN = ln N. Broj eje iracionalno, topribližna vrijednost 2,718281828. To je granica kojoj broj teži(1 + 1 / n) n uz neograničeno povećanjen(cm. prva divna granica ).
Koliko god čudno izgledalo, prirodni logaritmi su se pokazali vrlo zgodnim pri izvođenju različitih vrsta operacija vezanih za analizu funkcija.Izračunavanje logaritama na osnovueizvršeno mnogo brže nego iz bilo kojeg drugog razloga.