მათემატიკა ბუნებაში: მაგალითები. მათემატიკა ბუნებაში, ნუმეროლოგია ცხოვრებაში ჰარმონიის ცნება

ჰარმონიის კონცეფცია. შემადგენლობის მათემატიკური კანონები

კომპოზიციის საფუძვლები გამოყენებით გრაფიკაში

ჯერ კიდევ უძველეს დროში ადამიანმა აღმოაჩინა, რომ ბუნებაში არსებული ყველა ფენომენი ერთმანეთთან არის დაკავშირებული, რომ ყველაფერი უწყვეტ მოძრაობაშია, იცვლება და რიცხვებში გამოხატვისას საოცარ ნიმუშებს ავლენს.

კლასიკური ეპოქის ძველ საბერძნეთში წარმოიშვა მრავალი სწავლება ჰარმონიის შესახებ. მათგან პითაგორას სწავლებამ ყველაზე ღრმა კვალი დატოვა მსოფლიო კულტურაში. პითაგორას მიმდევრებმა წარმოიდგინეს სამყარო, სამყარო, სივრცე, ბუნება და ადამიანი, როგორც ერთიან მთლიანობა, სადაც ყველაფერი ურთიერთდაკავშირებულია და ჰარმონიულ ურთიერთობებშია. ჰარმონია აქ მოქმედებს როგორც წესრიგის დასაწყისი - ქაოსის მოწესრიგება. ჰარმონია თანდაყოლილია ბუნებასა და ხელოვნებაში: ” იგივე კანონები არსებობს მუსიკალურ რეჟიმებსა და პლანეტებზეპითაგორელები და მათი მიმდევრები ეძებდნენ რიცხვით გამოხატულებას სამყაროში ყველაფრისთვის. მათ აღმოაჩინეს, რომ მათემატიკური პროპორციები ემყარება მუსიკას (სიგრძის თანაფარდობა ხმასთან, ინტერვალებს შორის ურთიერთობა, ბგერების თანაფარდობა აკორდებში. პითაგორელები ცდილობდნენ მათემატიკურად დაემტკიცებინათ სამყაროს ერთიანობის იდეა, ისინი ამტკიცებდნენ, რომ სამყაროს საფუძველი იყო სიმეტრიული გეომეტრიული ფორმები ადამიანის სხეულის პროპორციები და დაამტკიცა სილამაზის მათემატიკური კანონი, რომლის მიხედვითაც მოქანდაკე პოლიკლეიტოსმა შექმნა ქანდაკება „კანონი“.

საბერძნეთის ყველა კლასიკურ ხელოვნებას აქვს პითაგორას დოქტრინის შტამპი პროპორციების შესახებ. მისი გავლენა განიცადეს შუა საუკუნეების მეცნიერებმა, რენესანსის მეცნიერებამ და ხელოვნებამ, თანამედროვე დრომდე, დღემდე. შუა საუკუნეების მეცნიერმა ავგუსტინემ, პითაგორაელთა მიმდევრობით, სილამაზეს "რიცხობრივი თანასწორობა" უწოდა. სქოლასტიური ფილოსოფოსი ბონავენტურა წერდა: „არ არსებობს სილამაზე და სიამოვნება პროპორციულობის გარეშე და პროპორციულობა, პირველ რიგში, არსებობს რიცხვებში“. ლეონარდო და ვინჩიმ დაწერა ხელოვნებაში პროპორციის გამოყენების შესახებ თავის ტრაქტატში ფერწერის შესახებ: ” მხატვარი პროპორციული სახით განასახიერებს ბუნებაში დამალულ იმავე ნიმუშებს, რომლებიც მეცნიერმა იცის რიცხვითი კანონის სახით.".

ამრიგად, პროპორციულობა, მთლიანის ნაწილების პროპორციულობა, არის მთლიანის ჰარმონიის ყველაზე მნიშვნელოვანი პირობა და შეიძლება მათემატიკურად გამოხატული იყოს პროპორციების საშუალებით.

პროპორცია ნიშნავს ორი ან მეტი თანაფარდობის ტოლობას. პროპორციულობის რამდენიმე ტიპი არსებობს:

• მათემატიკური,
• ჰარმონიული,
• გეომეტრიული და ა.შ.

მათემატიკაში ორი ურთიერთობის ტოლობა გამოიხატება ფორმულით a:b=с:დდა მისი თითოეული წევრი შეიძლება განისაზღვროს დანარჩენი სამის მეშვეობით. ჰარმონიული პროპორციით არის 3 ელემენტი. ეს არის ან წყვილი განსხვავებები ზოგიერთი სამმაგი ელემენტის, ან თავად ამ ელემენტების, მაგალითად:

a:c=(a - c): (c - c)

გეომეტრიული პროპორციით ასევე არის მხოლოდ 3 ელემენტი, მაგრამ ერთი მათგანი საერთოა, a:b=c:c. გეომეტრიული პროპორციის ტიპი არის პროპორცია ე.წ. ოქროს რადიო"მხოლოდ ორი წევრი ჰყავს -" ა"და" ვეს არის მხატვრების საყვარელი პროპორცია, რომელსაც რენესანსში ეწოდებოდა "ღვთაებრივი პროპორცია".

ოქროს თანაფარდობა (გ.ს.)

ოქროს მონაკვეთის პროპორციის თავისებურება ის არის, რომ მასში ბოლო ტერმინი არის განსხვავება ორ წინა ტერმინს შორის, ე.ი.

a:b=c: (a -c)

• დამოკიდებულება ჰ. თან. რიცხვად გამოხატული 0,618 .
• პროპორცია ზ. თან. 1:0,618=0,618:0,382 .

თუ სწორხაზოვან სეგმენტს გამოხატავთ ერთის მიხედვით და შემდეგ დაყოფთ ორ სეგმენტად z-ში. s., მაშინ უფრო დიდი სეგმენტი იქნება 0.618-ის ტოლი, ხოლო პატარა სეგმენტი იქნება 0.382.

ნახ 2. სეგმენტის დაყოფა ოქროს კვეთის მიხედვით

პროპორციიდან გამომდინარე h. თან. აშენდა რიცხვების სერია, აღსანიშნავია იმით, რომ ყოველი მომდევნო რიცხვი ტოლი იყო ორი წინა რიცხვის ჯამის: 1, 1, 2, 3, 5, 8, 13, 21 და ა.შ. ეს სერია აღმოაჩინა იტალიელი მათემატიკოსი ფიბონაჩი და ამიტომ მას ფიბონაჩის სერიას უწოდებენ. მას აქვს თვისება, რომ ურთიერთობები მეზობელ ტერმინებს შორის, სერიების რიცხვების ზრდასთან ერთად, სულ უფრო უახლოვდება O, b18-ს, ანუ თანაფარდობას 3. თან.

პროპორციები თ. თან. მეცნიერები ასოცირდება ორგანული ნივთიერებების განვითარებასთან. თ. თან. იგი აღმოჩენილი იყო ცოცხალი ბუნების ობიექტებში - ჭურვების, ხის, მზესუმზირის განლაგების, ადამიანის სხეულის აგებულებაში და ასევე დაფიქსირდა სამყაროს სტრუქტურაში პლანეტების განლაგებაში.

რაც შეეხება ს. თან. ასევე არსებობს გეომეტრიული ფორმების ელემენტები - ხუთკუთხედი, ვარსკვლავი.

მართკუთხედში h. თან. მხარეები ს.ს. ეს მართკუთხედი შეიცავს კვადრატს და პატარა ოთხკუთხედს h. თან. (მისი დიდი გვერდი არის თავდაპირველი მართკუთხედის პატარა მხარე.) ამიტომ შესაძლებელია აშენდეს pr-k z.s. კვადრატზე დაფუძნებული: კვადრატის გვერდი გაყოფილია შუაზე, გამოყვანილია დიაგონალი იმ წერტილიდან ზევით, რომლის დახმარებით კვადრატის მხარეს აგებულია პრ-კ ზ.ს.

ხაზების გადაკვეთის წერტილები, რომლებიც ქმნიან ვარსკვლავს, ყოფენ მათ სეგმენტებად ოქროს თანაფარდობის მიმართ. ეს პატარა მართკუთხედი ჰგავს დიდ ოთხკუთხედს, რომელიც შედგება კვადრატისა და პატარა მართკუთხედის h. s., ანუ ორივე ეს მართკუთხედი არის ოთხკუთხედი h. თან.

სხვა სიტყვებით რომ ვთქვათ, თუ თქვენ ამოჭრით z მართკუთხედს. გ.. კვადრატი, შემდეგ რჩება უფრო პატარა მართკუთხედი, რომლის გვერდები კვლავ იქნება z თანაფარდობით. თან. ამ პატარა მართკუთხედის კვადრატად და კიდევ უფრო პატარა მართკუთხედად დაყოფით, კვლავ მივიღებთ 3-ს მართკუთხედს. s., და ასე შემდეგ ad infinitum. თუ მრუდის კვადრატების წვეროებს დავაკავშირებთ, მივიღებთ ლოგარითმულ მრუდს, უსასრულოდ მზარდ სპირალს, რომელსაც ეწოდება "განვითარების მრუდი", "სიცოცხლის სპირალი", რადგან ის შეიცავს იდეას. უსასრულო განვითარება.

ბრინჯი. 4. ოთხკუთხედი დაახლოებით ოქროს თანაფარდობით, აგებულია ხუთკუთხედის ფუძეზე

სურ. 5. ოქროს კვეთის მართკუთხედის აგება კვადრატზე დაფუძნებული.

გაუთავებელი გამეორება თ. თან. და ოთხკუთხედის გაკვეთისას კვადრატი h. თან. ავლენს მთლიანის გამეორებას მის ნაწილებში, რაც მთლიანის ჰარმონიის ერთ-ერთი პირობაა. ეს არის მართკუთხედის გ.ს. აღმოაჩინეს მხატვრებმა და დაიწყეს ს. თან. როგორც ჰარმონიზაციის გზა, პროპორციების გზა. ფიდიასმა გამოიყენა ზ. თან. აკროპოლისის მშენებლობის დროს (ძვ. წ. V ს.)

ბრინჯი. 6. ლოგარითმული მრუდი „სიცოცხლის სპირალი“

ბრინჯი. 7. წერილის აგება ლუკა პაჩიოლის წიგნიდან „ღვთაებრივი პროპორციის შესახებ“

ბერძენი ხელოსნები ჭურჭლის შექმნისას გოგირდსაც იყენებდნენ. თან. რენესანსის დროს თ. თან. გამოიყენება არა მხოლოდ არქიტექტურაში, ქანდაკებაში, ფერწერაში, არამედ პოეზიასა და მუსიკაში. დიურერი, ლეონარდო და ვინჩი და მისი სტუდენტი ლუკა პაჩიოლი იყენებდნენ ს. თან. ასოების ჰარმონიული პროპორციების ძიებაში. მართკუთხედი h. თან. ვხვდებით როგორც შუა საუკუნეების ხელნაწერი წიგნების პროპორციებში, ისე თანამედროვე წიგნებში, ვინაიდან წვრილი პროპორციები თ. თან. საშუალებას გაძლევთ ლამაზად მოაწყოთ წიგნის გვერდის სივრცე და გაავრცელოთ.

ბრინჯი. 8. შუა საუკუნეების ხელნაწერის იდეალური პროპორციების სქემა.

გვერდის პროპორციებია 2:3, ხოლო ასოს მიერ დაკავებული სიბრტყე ოქროს კვეთის პროპორციაშია.

ბრინჯი. 9. მოცემული ფორმატის აკრეფის ზოლის ზომის განსაზღვრის ერთ-ერთი გზა.

პროპორციულობა არის მთლიანის ნაწილების ერთ პროპორციულ წესრიგამდე მიყვანა.

მეოცე საუკუნეში კვლავ გაიზარდა ინტერესი ოქროს თანაფარდობის, როგორც პროპორციული მეთოდის მიმართ.

მან მიიპყრო არქიტექტორების ყურადღება. საბჭოთა არქიტექტორი ჟოლტოვსკი და ფრანგი კორბუზიე მკურნალობდნენ სანიტარული პრობლემებით. თან. და გამოიყენა იგი თავის არქიტექტურულ პრაქტიკაში, კორბუზიემ შექმნა პროპორციების მთელი სისტემა, რომელიც ეფუძნება ოქროს თანაფარდობის სერიებისა და ადამიანის სხეულის პროპორციებს და უწოდა მას "მოდულორი", რაც ლათინურად ნიშნავს "რიტმულად გაზომვას".

ბრინჯი. 9. მოდული (გამარტივებული დიაგრამა)

ბრინჯი. 10. Modulor-ის საფუძველზე მართკუთხედის გაყოფის ვარიანტები.

კორბუზიეს მოდული წარმოადგენს რიცხვების ჰარმონიულ სერიას, რომლებიც დაკავშირებულია ერთ სისტემაში და განკუთვნილია არქიტექტურასა და დიზაინში გამოსაყენებლად - მთელი გარემოს ჰარმონიზაციისთვის, რომელშიც ადამიანი ცხოვრობს. კორბუზიე ოცნებობდა მთელი არქიტექტურული და ობიექტის გარემოს რესტრუქტურიზაციაზე Modulor-ის დახმარებით. მან თავად შექმნა არქიტექტურის რამდენიმე შესანიშნავი ნიმუში, მაგრამ მოდულორის უფრო ფართო გამოყენება არსებულ პირობებში გამორიცხული იყო.

მოდულორი გამოიყენებოდა დიზაინში და გრაფიკულ დიზაინში - ბეჭდური პუბლიკაციების დიზაინში. ნახ. ნახაზი 16 გვიჩვენებს 3:4 მართკუთხედის გაყოფის ვარიანტებს, რომლებიც მოცემულია კორბუზიეს მიერ მოდულორის გამოყენებით დიზაინის შესაძლებლობების დემონსტრირებისთვის.

დ.ჰამბიჯმა ხელი შეუწყო ოქროს მონაკვეთის პროპორციულობისა და გამოყენების საკითხის განვითარებას. 2020 წელს ნიუ-იორკში გამოიცა მისი წიგნი „დინამიური სიმეტრიის ელემენტები“. ჰამბიჯმა გამოიკვლია დინამიური სიმეტრია, რომელიც მან აღმოაჩინა მართკუთხედების სერიაში, მხატვრების მიერ მისი პრაქტიკული გამოყენების მიზნით კომპოზიციურ მშენებლობაში. ის ცდილობს გამოავლინოს საიდუმლოებები, რომლებსაც ძველი ბერძნები იყენებდნენ ფორმის ჰარმონიული გადაწყვეტის მისაღწევად. მისი ყურადღება მიიპყრო მართკუთხედების თვისებებმა, რომლებიც ქმნიან მწკრივს, სადაც ყოველი მომდევნო მართკუთხედი აგებულია წინას დიაგონალზე, დაწყებული C2 კვადრატის დიაგონალით. ეს არის მართკუთხედები C4, C5 (პატარა გვერდით კვადრატის გვერდის ტოლი, აღებული როგორც ერთი). (სურ. 17). სერიის კულმინაციაა მართკუთხედი T5, რომელსაც აქვს განსაკუთრებული ჰარმონიული თვისებები და "დაკავშირებულია" ოქროს მონაკვეთის მართკუთხედთან (ეს ქვემოთ იქნება განხილული).

ბრინჯი. 11. დინამიური ჰამბიჯის ოთხკუთხედების სერია.

ჰამბიჯი ასევე განიხილავს ამ მართკუთხედების გვერდებზე აგებულ კვადრატების ფართობებს და აღმოაჩენს შემდეგ დინამიკას: სავარჯიშო C2-ში უფრო დიდ მხარეს აგებულ კვადრატს აქვს 2-ჯერ დიდი ფართობი ვიდრე პატარა მხარეს აგებულ კვადრატს. სავარჯიშო C3-ში უფრო დიდი მხარის კვადრატი 3-ჯერ დიდია პატარა მხარის კვადრატზე და ა.შ. ამ გზით იქმნება არეების დინამიური სერია, რომელიც შედგება მთელი რიცხვებისგან.

ჰემბიჯი ამტკიცებს, რომ ძველი ბერძნები ამ პრინციპს იყენებდნენ კომპოზიციურ გადაწყვეტილებებში. დროის სერიების მართკუთხედები, რომლებზეც ჩვენ ვისაუბრეთ, არის ჰემბიჯის კომპოზიციური სისტემის ძირითადი სფეროები. თითოეული ეს ოთხკუთხედი შეიძლება დაიყოს ცალკეულ ნაწილებად და წარმოქმნას ახალი კომპოზიციური გადაწყვეტილებები და ახალი თემები. მაგალითად, მართკუთხედი C5 შეიძლება დაიყოს კვადრატად და ოქროს თანაფარდობის ორ ოთხკუთხედად. ოქროს თანაფარდობის მართკუთხედი შეიძლება დაიყოს კვადრატად და ოქროს თანაფარდობის მართკუთხედად, ასევე შეიძლება დაიყოს თანაბარ ნაწილებად და ვლინდება შემდეგი ნიმუში: შუაზე გაყოფისას ის მისცემს ორ ოთხკუთხედს, რომელთაგან თითოეულს ექნება ორი ოქროსფერი. მართკუთხედების თანაფარდობა. როდესაც სამ ნაწილად იყოფა, თითოეულ მესამედში არის სამი ოქროს თანაფარდობის მართკუთხედი. 4 ნაწილად გაყოფისას - ოთხი მართკუთხედი თ. თან. მთავარი მართკუთხედის თითოეულ მეოთხედში.

პროპორციულ სისტემებს შორის, რომლებიც გამოიყენება არქიტექტურაში, დიზაინსა და გამოყენებითი გრაფიკაში, უნდა აღინიშნოს „სასურველი რიცხვების“ სისტემები და სხვადასხვა მოდულური სისტემები.

"სასურველი ნომრები" - გეომეტრიული პროგრესიის რიცხვების სერია, სადაც ყოველი მომდევნო რიცხვი წარმოიქმნება წინა რიცხვის რაიმე მუდმივ მნიშვნელობაზე გამრავლებით. სასურველი სერიიდან ნომრები გამოიყენება შეფუთვის დიზაინში, სარეკლამო პლაკატების შემადგენლობაში. ისინი უზრუნველყოფენ ფორმის რიტმული განვითარება ასევე გვხვდება უძველესი ფორმების ვაზების მშენებლობაში და თანამედროვე მანქანაში.

ცნობილი პროპორციული სისტემა არის ე.წ. იტალიის წოდებები", რომლებიც ეფუძნება ფიბონაჩის სერიის პირველ რიცხვებს - 2, 3, 5. თითოეული ეს რიცხვი, გაორმაგებული, ქმნის ერთმანეთთან ჰარმონიულად დაკავშირებულ რიცხვთა სერიას:

• 2 - 4, 8, 16, 32, 64 და ა.შ.
• 3 - 6, 12, 24 48, 96
• 5 - 10, 20, 40, 80, 160

პროპორციულობა დაკავშირებულია ცნებებთან პროპორციულობადა ზომები. მთლიანისა და მისი ნაწილების გაზომვის ერთ-ერთი გზაა მოდული. მოდული- ზომა ან ელემენტი, რომელიც არაერთხელ მეორდება მთლიანობაში და მის ნაწილებში. მოდული(ლათინური) ნიშნავს ზომას. სიგრძის ნებისმიერი ზომა შეიძლება იყოს მოდული. ბერძნული ტაძრების მშენებლობისას ასევე გამოიყენებოდა მოდული პროპორციულობის მისაღწევად. მოდული შეიძლება იყოს სვეტის რადიუსი ან დიამეტრი, მანძილი სვეტებს შორის.

ვიტრუვიუსი, I საუკუნის რომაელი არქიტექტორი. ძვ.წ ე., თავის ტრაქტატში არქიტექტურის შესახებ, მან დაწერა, რომ პროპორცია არის კორესპონდენცია მთელი ნაწარმოების წევრებსა და მის მთლიანობას შორის - ორიგინალად აღებულ ნაწილთან მიმართებაში, რომელზეც დაფუძნებულია ყველა პროპორციულობა, ხოლო პროპორციულობა არის მკაცრი ჰარმონია. თავად სტრუქტურის ცალკეული ნაწილების და ცალკეული ნაწილებისა და ერთი კონკრეტული ნაწილის მთლიანობის შესაბამისობა, როგორც ორიგინალი.

გამოყენებითი გრაფიკაში მოდული ფართოდ გამოიყენება წიგნების, ჟურნალების, გაზეთების, კატალოგების, პროსპექტების და ყველა სახის ბეჭდური პუბლიკაციების დიზაინში. მოდულური ბადეების გამოყენება ხელს უწყობს ტექსტებისა და ილუსტრაციების მოწყობას და ხელს უწყობს კომპოზიციური ერთიანობის შექმნას. ბეჭდური პუბლიკაციების მოდულური დიზაინი ეფუძნება ვერტიკალური და ჰორიზონტალური ხაზების ერთობლიობას, რომლებიც ქმნიან ქსელს, ყოფს ფურცელს (გვერდს) ოთხკუთხედებად, რომლებიც შექმნილია ტექსტის, ილუსტრაციების და მათ შორის სივრცეების გასანაწილებლად. ეს მართკუთხა მოდული (შეიძლება იყოს რამდენიმე მათგანი) განსაზღვრავს ბეჭდურ პუბლიკაციაში მასალის რიტმულად ორგანიზებულ განაწილებას.

არსებობს სხვადასხვა ნიმუშებისა და სირთულის ხარისხის ბადეები. ა. ჰურლბერტი თავის წიგნში „გრიდი“ მოჰყავს ჟურნალების, წიგნებისა და გაზეთების მოდულური ბადეების მაგალითებს.

მოდულური ბადე არ უნდა აგვერიოს ტიპოგრაფიულ ბადეში, რომელიც განსაზღვრავს ველების ზომას და აკრეფის გვერდის ფორმატს. რა თქმა უნდა, მოდულურმა ბადემ, რამდენადაც ის ეხება ბეჭდურ პუბლიკაციებს, უნდა გაითვალისწინოს ხაზების ზომები, ასოების სიმაღლე და სივრცეების ელემენტები ტიპოგრაფიულ ზომებში (კვადრატები, ციცეროსი, წერტილები), რათა სწორად განლაგდეს ნაბეჭდი მასალა. გვერდზე.

ქსელის სისტემა, მისი მკაფიო მოდულური ბაზის წყალობით, საშუალებას გაძლევთ დანერგოთ ელექტრონული პროგრამები პუბლიკაციის დიზაინის პროცესში. გამოყენებითი, სამრეწველო გრაფიკაში, მოდულური ბადე გამოიყენება ყველა სახის სარეკლამო პუბლიკაციების დიზაინში და, კერძოდ, გრაფიკული კორპორატიული სტილის დიზაინში. მოდულური ბადე გამოიყენება სხვადასხვა ნიშნების დიზაინში, ვიზუალური კომუნიკაციის ნიშნები, სავაჭრო ნიშნები და ა.შ.

ბრინჯი. 14. მოდულური ბადის საფუძველზე აგებული სავაჭრო ნიშანი.

ბრინჯი. 15. მიუნხენის ოლიმპიური თამაშების საკომუნიკაციო ნიშანი. აგებულია მოდულურ ბადეზე

მოდულური ბადეები ხშირად ეფუძნება კვადრატს. Square არის ძალიან მოსახერხებელი მოდული. იგი ფართოდ გამოიყენება როგორც მოდული თანამედროვე ავეჯის ინდუსტრიაში, კერძოდ, ასაწყობი ავეჯის, „კედლების“ მშენებლობაში.

ორმაგი კვადრატი დიდი ხანია ცნობილია, როგორც ტრადიციული იაპონური სახლის მოდული, სადაც ოთახების ზომები იყო იმის მიხედვით, თუ რამდენჯერ დაიდო იატაკზე ორმაგი კვადრატის პროპორციების მქონე ტატამი.

გამოყენებითი გრაფიკაში კვადრატი გამოიყენება ალბომების პროსპექტებისა და საბავშვო წიგნების ფორმატებისთვის, მაგრამ ასევე განსაზღვრავს ამ გამოცემების შიდა სივრცეს. კვადრატული მოდული ასევე შეიძლება გამოყენებულ იქნას არა კვადრატულ ფორმატში.

მოვიყვანოთ კვადრატული მოდულის კვადრატულ ფორმატში გამოყენების მაგალითი: სამსვეტიანი ტექსტის აკრეფით, ტექსტისა და ილუსტრაციებისთვის გამოყოფილი მთელი ფართობი იყოფა 9 კვადრატად. თუ სვეტის სიგანე მითითებულია როგორც 1, მაშინ კვადრატი იქნება 1x1. ამ შემთხვევაში, ილუსტრაციებმა შეიძლება დაიკავოს არეები: 1x1, 1x2, 1x3, 2x2, 2x3, 3x3, 2x1 და ა. ხელოვნებისა და დიზაინის ნაწარმოებების კომპოზიციურ სტრუქტურაში მნიშვნელოვანია მართკუთხედების და სხვა გეომეტრიული ფორმების პროპორციები, რომლებშიც ჯდება მოცემული ნამუშევარი ან მისი ძირითადი ნაწილები. აქედან გამომდინარე, უნდა განვიხილოთ მართკუთხედები, რომლებიც ყველაზე ფართოდ გამოიყენება მათი ჰარმონიული თვისებების გამო (ოქროს თანაფარდობის მართკუთხედი ზემოთ იყო განხილული). მოდი ისევ მოედანს შევხედოთ. მოედანი, როგორც სტრუქტურული ფორმა, დიდი ხანია ცნობილია. მან მიიპყრო ძველი სამყაროსა და რენესანსის მხატვრების ყურადღება.

ლეონარდო და ვინჩის ნახატი ასახავს კვადრატისა და წრის კავშირს ძველთათვის ცნობილ ადამიანის ფიგურასთან (ვიტრუვიუსი). რენესანსის მხატვრები - გერმანელი დიურერი, იტალიელი პაჩიოლი, ფრანგი ტორი, ასოების მოხაზულობის შემუშავებისას, კვადრატის ფორმიდან გამომდინარეობდნენ, ასო თავისი ყველა ელემენტით ჯდება კვადრატში (ნახ. 12), თუმცა არა ყველა ასო. უტოლდებოდა კვადრატს, თუმცა ზოგადი კომპოზიციური სტრუქტურა განისაზღვრა კვადრატში. კვადრატი არის სტაბილური, სტატიკური ფიგურა. ასოცირდება რაღაც უმოძრაო, სრული. ძველ სამყაროში, ზოგიერთ ხალხში, კვადრატის გამოსახულება სიკვდილის სიმბოლიკასთან იყო დაკავშირებული. (ამ მხრივ საინტერესოა აღინიშნოს, რომ კვადრატული პროპორციები ბუნებაში გვხვდება უსულო ნივთიერების ფორმებში, კრისტალებში). სტატიკური სისრულის გამო, კვადრატი გამოიყენება გამოყენებით გრაფიკაში, ვიზუალური კომუნიკაციების სფეროში, წრის ფორმასთან ერთად, როგორც ელემენტი, რომელიც იპყრობს ყურადღებას, ასევე ზღუდავს სივრცეს, რომელშიც არის ინფორმაცია კონცენტრირებული.

ოქროს თანაფარდობის მართკუთხედისა და კვადრატის გარდა, ჩვენთვის ყველაზე დიდი ინტერესია მართკუთხედები Ts2 და Ts5. კლასიკური ეპოქის ძველი ბერძნები ამ მართკუთხედებს ამჯობინებდნენ. რა არის საინტერესო ამ მართკუთხედში? ვერტიკალურად და ჰორიზონტალურად ორ ნაწილად იყოფა, ის აღადგენს თავის პროპორციებს. ეს ოთხკუთხედი შეიძლება დაიყოს კვადრატად და ოქროს თანაფარდობის ორ პატარა ოთხკუთხედად. გარდა ამისა, იგი გვიჩვენებს ოქროს თანაფარდობის ორ ოთხკუთხედს, რომლებიც ერთმანეთს კვადრატის ზომით გადაფარავს. დარჩენილი ნაწილიც ოქროს კვეთის მართკუთხედია. ამრიგად, მართკუთხედი C5 ავლენს რიტმულ თვისებებს. მასში ჩნდება ლამაზი სიმეტრია (პატარა მართკუთხედი გ.ს. + კვადრატი + პატარა მართკუთხედი გ.ს.).

ბრინჯი. 16. ოთხკუთხედის რიტმული თვისებები

ჰამბიჯი იძლევა ბოსტონის მუზეუმის ბერძნული ჭიქის კომპოზიციურ დიაგრამას: თასი ჯდება (სახელურების გარეშე) ჰორიზონტალურად წაგრძელებულ ოთხკუთხედში C5. გადის საზღვარი თასსა და მის ფეხს შორის. ფეხის ძირის სიგანე ტოლია თასის სიმაღლისა და ტოლი კვადრატის გვერდის, რომელიც მდებარეობს C5 ოთხკუთხედის ცენტრში. ფეხი ჯდება ორ პატარა ოთხკუთხედად. ს., მოჭრილი კვადრატიდან ც5 გამზირის ძირამდე ჰორიზონტალური ხაზით და გადის დიდი ოთხკუთხედების h ორი დიაგონალის გადაკვეთის წერტილში. თან. თანამედროვე მხატვრულ დიზაინში ასევე ფართოდ გამოიყენება Ts5 მართკუთხედი. მას ვხვდებით მანქანების, ჩარხების და სხვა პროდუქტების პროპორციებში. გამოყენებითი გრაფიკაში - პროსპექტების, ბუკლეტების, შეფუთვის ფორმატებში; სახვით ხელოვნებაში, მონუმენტურ ხელოვნებაში, სურათის სიბრტყის პროპორციებში, სურათის კომპოზიციურ სტრუქტურაში.

Ts2 მართკუთხედი ასევე ფართოდ გამოიყენება, განსაკუთრებით გამოყენებითი გრაფიკის სფეროში. იგი გამოიყენება როგორც ქაღალდის ფორმატი საქმიანი დოკუმენტებისთვის, რადგან მას აქვს საოცარი თვისება - როდესაც იყოფა შუაზე, არ იცვლის პროპორციებს. როდესაც იყოფა, წარმოიქმნება მრავალი მსგავსი ოთხკუთხედი, რომლებიც ჰარმონიულად არის დაკავშირებული ფორმის ერთიანობით. ნახ. სურათი 18 გვიჩვენებს მართკუთხედების გამოსახულებას, რომლებიც გამოიყენება კომპოზიციურ მშენებლობაში მათი გვერდების ჰარმონიული ურთიერთობის გამო.

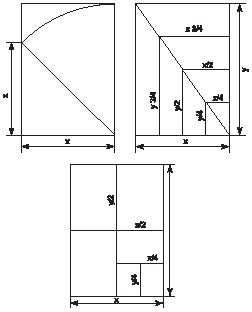
ბრინჯი. 17. მხარეთა პროპორციები pr-ke Ts2-ში, გამოყენებული პორტმანის სტანდარტში.

ბრინჯი. 18. გვერდების ჰარმონიული მიმართებები მართკუთხედებში.

ქვემოთ მოცემულია pr-kov Ts2, Ts3, Ts4, Ts5 რიცხვითი შეფარდება მათ საპასუხო რიცხვებთან, რომლებთანაც ისინი ჰარმონიულ ურთიერთობაში არიან. (რიცხვის საპასუხო არის რიცხვი, რომელიც მიღებულია ერთი მოცემულ რიცხვზე გაყოფით.) თუ მართკუთხედის პატარა გვერდს ავიღებთ ერთად, მაშინ მართკუთხედისთვის რიცხვი (მართკუთხედის უფრო დიდი გვერდის შესაბამისი) = 1,4142, ხოლო ორმხრივი რიცხვი = 0,7071; pr-ka Ts3 ნომერი = 1,732, საპასუხო ნომერი = 0,5773; pr-ka Ts4 ნომერი = 2, საპასუხო რიცხვი = 0.5; პრ-კა ც5 ნომრისთვის = 2.236; ორმხრივი=0,4472; პრ-კა" z.s. ნომერი = 1.618, საპასუხო ნომერი = 0.618.

Ts2 პროექტის საფუძველზე განხორციელდა წიგნების, ნაშრომების, საქმიანი დოკუმენტების, ღია ბარათების, პლაკატების, საქაღალდეების და გამოყენებითი გრაფიკასთან დაკავშირებული სხვა ობიექტების ფორმატების სტანდარტიზაცია და უნიფიცირება. ეს სტანდარტი, რომელიც ცნობილია როგორც Dr. Porstmann სტანდარტი, მიღებულია ევროპის 17 ქვეყანაში. სტანდარტი ეფუძნებოდა 841X1189 მმ ფორმატს და 1 მ 2 ფართობს. დანარჩენი ფორმატები, რომლებიც ქმნიან მის აქციებს, გამომდინარეობს მისგან:

• 1 მ 2 - 841 X 1189 მმ
• 1/2მ 2 - 594 Х841მმ
• 1/4 მ 2 - 420 X 594 მმ
• 1/8 მ 2 - 297Х420 მმ (ორმაგი ფურცელი)
• 1/16 მ 2 - 210Х 297 მმ (ფურცელი საქმიანი მიმოწერისთვის, ფორმები)
• 1/32 მ 2 - 148Х210 მმ (ნახევარი ფურცელი საქმიანი მიმოწერისთვის, ფორმები)
• 1/64 მ 2 - 105 Х148 მმ (საფოსტო)
• 1/128 მ 2 - 74Х105 მმ (სავიზიტო ბარათი)

სტანდარტი ასევე ითვალისწინებს დამატებით ფორმატებს 1000X1414 და 917X1297 და მათ აქციებს. კონვერტებისთვის შემოთავაზებულია შემდეგი ზომები: 162X229 და 114X162. (სტანდარტი სრულად არ არის მოცემული).

ბრინჯი. 19. მართკუთხედის ნაწილებად დაყოფა: 1/2, 1/4, 1/8, 1/16,1/64.

ვინაიდან საქმიანი ქაღალდებისა და დოკუმენტაციის დამუშავება გულისხმობს არა მხოლოდ კონვერტებს და საქაღალდეებს, რომლებიც შეესაბამება მათ ზომასა და ფორმატს, არამედ კონტეინერებს, რომლებშიც ინახება დოკუმენტაცია, შესაბამისად, საჭიროა შესაბამისი ავეჯი: მაგიდები, კარადები, თაროები. ავეჯის ზომები და პროპორციები, თავის მხრივ, მიუთითებს შენობის ინტერიერის ხასიათზე. ამრიგად, ჩნდება ჰარმონიზებული ინტერიერის ელემენტების სრული სისტემა, რომელიც ექვემდებარება ერთ მოდულურ პრინციპს.

პროპორციული ურთიერთობები უნდა არსებობდეს არა მხოლოდ მთლიანის ცალკეულ ნაწილებს შორის, არამედ ობიექტებს შორის, რომლებიც ქმნიან ობიექტების ჯგუფებს, რომლებიც დაკავშირებულია ერთი სტილით და ფუნქციური ამოცანებით. მაგალითად, კორპორატიული იდენტურობის სისტემაში შემავალ ობიექტებს შორის.

ადამიანის გარშემო არსებული ობიექტები უნდა იყოს ჰარმონიზებული არა მხოლოდ ერთმანეთთან მიმართებაში, არამედ დაკავშირებული იყოს ადამიანთან ერთი საზომით, მის ფიზიკურ სტრუქტურასთან. ანტიკური ხანის არქიტექტორები თვლიდნენ, რომ არქიტექტურის ნაწილების ურთიერთობა ერთმანეთთან და მთლიანთან უნდა შეესაბამებოდეს ადამიანის სხეულის ნაწილებს და მათ ურთიერთობებს. ანალოგიურად, კორბუზიეს მოდული გამოდის ადამიანის სხეულის ზომებიდან და მასში არსებული ოქროს მონაკვეთის ურთიერთობებიდან (მანძილი დედამიწიდან მზის წნულამდე და მანძილი მზის წნულიდან გვირგვინამდე არის უკიდურესი და საშუალო ოქროს მონაკვეთის პროპორციები...

ფართომასშტაბიანი ურთიერთობები საგნებს, ობიექტურ გარემოსა და ადამიანს შორის მოქმედებს როგორც ჰარმონიზაციის საშუალება, რადგან მასშტაბი არის პროპორციულობის ერთ-ერთი გამოვლინება, რომელიც ადგენს ფარდობით განზომილებებს ადამიანსა და საგანს შორის - არქიტექტურაში, დიზაინში, გამოყენებით ხელოვნებაში. კერძოდ, გამოყენებით გრაფიკაში, წიგნების ხელოვნებაში. ამრიგად, პლაკატების ზომები და ფორმატები და ნებისმიერი ობიექტი, რომელიც ემსახურება ვიზუალური კომუნიკაციის მიზნებს - ნიშნები, საგზაო ნიშნები და ა. . იგივე ეხება წიგნის დიზაინის სფეროს და ყველა სახის ბეჭდურ რეკლამას და შეფუთვას.

Სიმეტრია.

პროპორციულად და პროპორციულად ვლინდება რაოდენობრივი ურთიერთობები მთელისა და მთელის ნაწილებს შორის. ბერძნებმა ასევე დაამატეს მათ სიმეტრია და მიიჩნიეს პროპორციულობის სახეობად - როგორც მისი განსაკუთრებული შემთხვევა - იდენტობა. ის, ისევე როგორც პროპორცია, ითვლებოდა ჰარმონიისა და სილამაზის აუცილებელ პირობად.

სიმეტრია ემყარება მსგავსებას. ეს ნიშნავს ელემენტებსა და ფიგურებს შორის ასეთ ურთიერთობას, როდესაც ისინი იმეორებენ და აბალანსებენ ერთმანეთს. მათემატიკაში სიმეტრია ნიშნავს ფიგურის ნაწილების განლაგებას ღერძთან ან სიმეტრიის ცენტრთან შედარებით მისი გადაადგილებისას.

არსებობს სხვადასხვა სახის სიმეტრია. სიმეტრიის უმარტივესი ტიპია სარკე (ღერძული), რომელიც ხდება მაშინ, როდესაც ფიგურა ბრუნავს სიმეტრიის ღერძის გარშემო. სიმეტრიას, რომელიც ჩნდება, როდესაც ფიგურა ბრუნავს ბრუნვის ცენტრის გარშემო, ეწოდება ცენტრალური. ბურთს აქვს სიმეტრიის უმაღლესი ხარისხი, რადგან მის ცენტრში უსასრულო რაოდენობის ღერძი და სიმეტრიის სიბრტყეები იკვეთება. აბსოლუტური, ხისტი სიმეტრია დამახასიათებელია უსულო ბუნების - კრისტალების (მინერალები, ფიფქები).

ორგანულ ბუნებას და ცოცხალ ორგანიზმებს ახასიათებთ არასრული სიმეტრია (კვაზისიმეტრია), (მაგალითად, ადამიანის აგებულებაში). სიმეტრიის დარღვევა, ასიმეტრია (სიმეტრიის ნაკლებობა) ხელოვნებაში გამოიყენება როგორც მხატვრული საშუალება. სწორი სიმეტრიიდან უმნიშვნელო გადახრა, ანუ გარკვეული ასიმეტრია, არღვევს წონასწორობას, იპყრობს ყურადღებას, შემოაქვს მოძრაობის ელემენტს და ქმნის ცოცხალი ფორმის შთაბეჭდილებას. სიმეტრიის სხვადასხვა ტიპს განსხვავებული გავლენა აქვს ესთეტიკურ გრძნობაზე:

• სარკის სიმეტრია - წონასწორობა, სიმშვიდე;
• ხვეული სიმეტრია იწვევს მოძრაობის განცდას...

ხზმბიჯი ყველა მარტივ გეომეტრიულ ფიგურას კლასიფიცირებს სტატიკური სიმეტრიად (სიმეტრიის ყველა ტიპს ყოფს სტატიკურ და დინამიკურად) და მოიცავს სპირალს, როგორც დინამიურ სიმეტრიას. სტატიკური სიმეტრია ხშირად ემყარება ხუთკუთხედს (ყვავილის ან ნაყოფის მოჭრა) ან კვადრატს (მინერალებში). ხელოვნებაში მკაცრი მათემატიკური სიმეტრია იშვიათად გამოიყენება.

ბრინჯი. 20. სიმეტრიის სახეები: სარკე, ხვეული, ცენტრალური, ათვლის.

ბრინჯი. 21. ჰოგარტის "მადლისა და სილამაზის ხაზი".

სიმეტრია ასოცირდება შუასა და მთლიანის ცნებასთან. ძველ ბერძნულ ფილოსოფიასა და ხელოვნებაში ცნება „შუა, ცენტრი“ ასოცირდება ყოფიერების მთლიანობის იდეასთან. შუა - "უკიდურესობის თავიდან აცილება" (არისტოტელე) - ნიშნავს წონასწორობის პრინციპს. ბერძენი ყველგან ხედავდა რაღაც მთლიანობას და ეს ნიშნავს, რომ მან უპირველეს ყოვლისა დააფიქსირა დაკვირვებული ან უცხო ობიექტის ცნება... პროპორციების, ზომების, სიმეტრიის ან ჰარმონიის შესახებ უძველესი სწავლება წარმოუდგენელია.

ჰარმონია

ჰარმონია დიალექტიკური ცნებაა. ძველი ბერძნული მითოლოგიის მიხედვით, ჰარმონია ომის ღმერთის არესისა და სიყვარულისა და სილამაზის ქალღმერთი აფროდიტეს ქალიშვილია, ანუ მასში საპირისპირო, მეომარი პრინციპებია შერწყმული. ამიტომ, ჰარმონიის ცნება მოიცავს კონტრასტს, როგორც აუცილებელ პირობას. კონტრასტი ხელს უწყობს მრავალფეროვნებას და მრავალფეროვნებას, რომლის გარეშეც ჰარმონია წარმოუდგენელია.

"ჰარმონია არის ბევრის ერთიანობა და მათთან შეთანხმება, ვინც არ ეთანხმება"(ფილოლაუსი). ძველებმა ეს იცოდნენ. მე-18 საუკუნის მხატვარმა ჰოგარტმა აღმოაჩინა, რომ ჰარმონიის არსი ერთიანობასა და მრავალფეროვნებაშია. იგი თაყვანს სცემდა ტალღოვან ხაზს, რომელიც მას მიაჩნდა " სილამაზის და მადლის ხაზი", რადგან ეს არის ერთიანობისა და მრავალფეროვნების კონკრეტული განსახიერება. მრავალფეროვნების გარეშე სილამაზე შეუძლებელია. ერთფეროვნება საბურავს. საპირისპიროს შეცვლაში ვლინდება დიალექტიკური ნიმუში - უარყოფის უარყოფა. ხელოვნების ხილულ გამოსახულებებში გამოხატულია. რიტმისა და კონტრასტის საშუალებით ჰარმონიის მნიშვნელობა არის ქაოსის შეკავება.

მაგრამ ის ამას საპირისპირო პრინციპების ბრძოლით აკეთებს. საპირისპირო პრინციპების გაერთიანებით ჰარმონია აბალანსებს მათ, შემოაქვს ზომა და შეთანხმება, აწესრიგებს მათ და ჯილდოდ იღებს სილამაზეს.

სიმეტრია, პროპორციები, რიტმი, კონტრასტი, მთლიანობა - ისინი, რომლებიც ქმნიან ჰარმონიას, ობიექტურად დაკავშირებულია ბუნებასთან, მატერიის მოძრაობასთან და განვითარებასთან. ჩვენი ესთეტიკური იდეები მჭიდროდ არის დაკავშირებული ამ ცნებებთან. თუმცა, ადამიანის სოციალური არსებობა სხვადასხვა ეპოქაში ჰარმონიის კატეგორიებს სხვადასხვა კუთხით უყურებდა და ამან განსაზღვრა მათი როლი სოციალურ ცხოვრებაში და ხელოვნებაში. სილამაზის იდეა განვითარდა და შეიცვალა. ჰარმონია დაიწყო არა როგორც რაოდენობრივი, არამედ თვისებრივი პრინციპის განხილვა, რომელიც აერთიანებს ფიზიკურ და სულიერ პრინციპებს.

თუ ძველი ბერძნები მშვენივრად მხოლოდ შეკვეთილ სილამაზეს თვლიდნენ და სიმეტრიისა და პროპორციების დარღვევას მახინჯად თვლიდნენ, შემდეგ ეპოქაში სილამაზის გამოვლინებები წესრიგის დარღვევაში, დისონანსში, აშკარა დისჰარმონიაში დაიწყო, რადგან ისინი სიცოცხლისთვის დამახასიათებელია. და, შესაბამისად, არიან სხვა ჰარმონიული სისტემის ნაწილი, რომელშიც ისინი პოულობენ ლოგიკას და მნიშვნელობას. "მშვენიერია ცხოვრება", - წერდა ჩერნიშევსკი. და ის არ დგას. ბუნებასა და ცხოვრებაში ჰარმონიის გამოჩენა უფრო ფართოა, ვიდრე ნებისმიერი კანონი, ნებისმიერ ჰარმონიულ სისტემას შეუძლია დაფაროს. და კაცობრიობა არასოდეს შეწყვეტს ახალი ჰარმონიული ურთიერთობების, კომბინაციების ძიებას და სხვა ჰერმონიული ნიმუშების გამოვლინების ძიებას. თუმცა ეს არ ნიშნავს იმას, რომ კლასიკურმა ჰარმონიამ აზრი დაკარგა. რაც უკვე აღმოჩენილია, ნაპოვნი ნიმუშები, მათი მათემატიკური დასაბუთება რჩება კაცობრიობის მარადიულ მემკვიდრეობად, საიდანაც აიღებს ყველა მომდევნო თაობა.

• გადადით შემდეგ ნაწილზე - ""

თუ გარშემო ყურადღებით დააკვირდებით, აშკარა ხდება მათემატიკის როლი ადამიანის ცხოვრებაში. კომპიუტერები, თანამედროვე ტელეფონები და სხვა აღჭურვილობა ყოველდღიურად გვყვება და მათი შექმნა შეუძლებელია დიდი მეცნიერების კანონებისა და გამოთვლების გარეშე. თუმცა, მათემატიკის როლი საზოგადოებაში მხოლოდ ასეთი აპლიკაციებით არ შემოიფარგლება. სხვაგვარად, მაგალითად, ბევრ ხელოვანს შეეძლო სუფთა სინდისით ეთქვა, რომ სკოლაში პრობლემების გადაჭრისა და თეორემების დამტკიცებისთვის დათმობილი დრო ტყუილად დაიკარგა. თუმცა ეს ასე არ არის. შევეცადოთ გაერკვნენ, რატომ არის საჭირო მათემატიკა.

ბაზა

პირველ რიგში, ღირს იმის გაგება, თუ რა არის მათემატიკა სინამდვილეში. ძველი ბერძნულიდან თარგმნილი, მისი სახელი ნიშნავს "მეცნიერებას", "სწავლას". მათემატიკა ემყარება ობიექტების ფორმის დათვლის, გაზომვისა და აღწერის ოპერაციებს. რომელზედაც დაფუძნებულია სტრუქტურის, წესრიგისა და ურთიერთობების ცოდნა. ისინი არიან მეცნიერების არსი. რეალური ობიექტების თვისებები მასში იდეალიზებულია და ფორმალური ენით არის დაწერილი. ასე გარდაიქმნება ისინი მათემატიკურ ობიექტებად. ზოგიერთი იდეალიზებული თვისება ხდება აქსიომები (განცხადებები, რომლებიც არ საჭიროებს მტკიცებულებას). ამ სხვა ჭეშმარიტი თვისებების შემდეგ მიღებულია. ასე ყალიბდება რეალური არსებული ობიექტი.

ორი განყოფილება

მათემატიკა შეიძლება დაიყოს ორ დამატებით ნაწილად. თეორიული მეცნიერება ეხება ინტრამათემატიკური სტრუქტურების ღრმა ანალიზს. გამოყენებითი მეცნიერება თავის მოდელებს აწვდის სხვა დისციპლინებს. ფიზიკა, ქიმია და ასტრონომია, საინჟინრო სისტემები, პროგნოზირება და ლოგიკა მუდმივად იყენებენ მათემატიკურ აპარატს. მისი დახმარებით ხდება აღმოჩენები, ნიმუშების აღმოჩენა და მოვლენების წინასწარმეტყველება. ამ თვალსაზრისით, მათემატიკის მნიშვნელობა ადამიანის ცხოვრებაში არ შეიძლება გადაჭარბებული იყოს.

პროფესიული საქმიანობის საფუძველი

ძირითადი მათემატიკური კანონების ცოდნისა და მათი გამოყენების უნარის გარეშე, თანამედროვე სამყაროში ძალიან რთული ხდება თითქმის ნებისმიერი პროფესიის სწავლა. არა მხოლოდ ფინანსისტები და ბუღალტერები არიან მათთან დაკავშირებული ნომრებითა და ოპერაციებით. ასეთი ცოდნის გარეშე ასტრონომი ვერ შეძლებს ვარსკვლავამდე მანძილის დადგენას და მის დასაკვირვებლად საუკეთესო დროს, ხოლო მოლეკულური ბიოლოგი ვერ გაიგებს, როგორ გაუმკლავდეს გენურ მუტაციას. ინჟინერი არ შეიმუშავებს მოქმედ სიგნალიზაციას ან ვიდეო თვალთვალის სისტემას და პროგრამისტი ვერ იპოვის მიდგომას ოპერაციულ სისტემასთან. ამ და სხვა პროფესიებიდან ბევრი უბრალოდ მათემატიკის გარეშე არ არსებობს.

ჰუმანიტარული მეცნიერებები

თუმცა, მათემატიკის როლი ადამიანის ცხოვრებაში, მაგალითად, რომელმაც თავი მიუძღვნა მხატვრობას ან ლიტერატურას, არც ისე აშკარაა. და მაინც, მეცნიერებათა დედოფლის კვალი ჰუმანიტარულ მეცნიერებებშიც არის.

როგორც ჩანს, პოეზია არის სუფთა რომანტიკა და შთაგონება, არ არის ადგილი ანალიზისა და გაანგარიშებისთვის. თუმცა, საკმარისია გავიხსენოთ ამფიბრაქების პოეტური ზომები) და მივხვდეთ, რომ მათემატიკას ამაშიც ჰქონდა ხელი. რიტმი, ვერბალური თუ მუსიკალური, ასევე აღწერილია და გამოითვლება ამ მეცნიერების ცოდნის გამოყენებით.

მწერლისა თუ ფსიქოლოგისთვის ხშირად მნიშვნელოვანია ისეთი ცნებები, როგორიცაა ინფორმაციის სანდოობა, ცალკეული ინციდენტი, განზოგადება და ა.შ. ყველა მათგანი ან უშუალოდ მათემატიკურია, ან აგებულია მეცნიერებათა დედოფლის მიერ შემუშავებული კანონების საფუძველზე და არსებობს მისი წყალობით და მისი წესების მიხედვით.

ფსიქოლოგია დაიბადა ჰუმანიტარული და საბუნებისმეტყველო მეცნიერებების კვეთაზე. მისი ყველა მიმართულება, თუნდაც ის, რომელიც მუშაობს ექსკლუზიურად სურათებთან, ეყრდნობა დაკვირვებას, მონაცემთა ანალიზს, მათ განზოგადებას და გადამოწმებას. აქ გამოიყენება მოდელირება, პროგნოზირება და სტატისტიკური მეთოდები.

Სკოლიდან

მათემატიკა არის ჩვენს ცხოვრებაში არა მხოლოდ პროფესიის დაუფლებისა და მიღებული ცოდნის განხორციელების პროცესში. ასეა თუ ისე, ჩვენ ვიყენებთ მეცნიერებათა დედოფალს დროის თითქმის ყოველ მომენტში. ამიტომ მათემატიკის სწავლება საკმაოდ ადრე იწყება. მარტივი და რთული ამოცანების გადაჭრით ბავშვი მხოლოდ შეკრებას, გამოკლებას და გამრავლებას არ სწავლობს. იგი ნელ-ნელა, საფუძვლებიდან, აცნობიერებს თანამედროვე სამყაროს სტრუქტურას. და ჩვენ არ ვსაუბრობთ ტექნიკურ პროგრესზე ან მაღაზიაში ცვლილების შემოწმების შესაძლებლობაზე. მათემატიკა აყალიბებს აზროვნების გარკვეულ მახასიათებლებს და გავლენას ახდენს ჩვენს დამოკიდებულებაზე სამყაროს მიმართ.

უმარტივესი, ყველაზე რთული, ყველაზე მნიშვნელოვანი

ალბათ ყველას ემახსოვრება ერთი საღამო მაინც საშინაო დავალების შესრულებისას, როცა სასოწარკვეთილი ყვირილი სურდათ: „არ მესმის, რისთვის არის მათემატიკა!“, გვერდზე გადააგდე საძულველი რთული და დამღლელი პრობლემები და მეგობრებთან ერთად ეზოში გაიქცნენ. სკოლაში და კიდევ უფრო გვიან, კოლეჯში, მშობლებისა და მასწავლებლების დარწმუნება, რომ „მოგვიანებით გამოგადგებათ“ გამაღიზიანებელი სისულელეა. თუმცა, გამოდის, რომ ისინი მართლები არიან.

ეს არის მათემატიკა და შემდეგ ფიზიკა, რომელიც გასწავლის მიზეზ-შედეგობრივი კავშირების პოვნას, აყალიბებს ჩვევას, ეძებო ყბადაღებული „საიდანაც ფეხები იზრდება“. ყურადღება, კონცენტრაცია, ნებისყოფა - ვარჯიშობენ იმ ძალიან საძულველი პრობლემების გადაჭრის პროცესშიც. თუ უფრო შორს წავალთ, ფაქტებიდან შედეგების გამოტანის, მომავლის მოვლენების პროგნოზირების და ასევე იგივეს გაკეთების უნარი ჩამოყალიბებულია მათემატიკური თეორიების შესწავლის დროს. მოდელირება, აბსტრაქცია, დედუქცია და ინდუქცია არის ყველა მეცნიერება და, ამავე დროს, ტვინის ინფორმაციასთან მუშაობის გზები.

და ისევ ფსიქოლოგია

ხშირად სწორედ მათემატიკა აძლევს ბავშვს იმის გამოცხადებას, რომ მოზარდები არ არიან ყოვლისშემძლეები და არ იციან ყველაფერი. ეს ხდება მაშინ, როდესაც დედა ან მამა, როცა პრობლემის გადაჭრაში დახმარებას სთხოვენ, უბრალოდ მხრებს იჩეჩებიან და აცხადებენ, რომ არ შეუძლიათ ამის გაკეთება. და ბავშვი იძულებულია თავად ეძებოს პასუხი, დაუშვას შეცდომები და ხელახლა შეხედოს. ასევე ხდება, რომ მშობლები უბრალოდ უარს ამბობენ დახმარებაზე. ”თქვენ თვითონ უნდა გააკეთოთ ეს”, - ამბობენ ისინი. და ისინი ამას სწორად აკეთებენ. მრავალსაათიანი მცდელობის შემდეგ ბავშვი მიიღებს არა მხოლოდ დასრულებულ საშინაო დავალებას, არამედ გადაწყვეტილებების დამოუკიდებლად პოვნის, შეცდომების აღმოჩენისა და გამოსწორების უნარს. და ეს ასევე არის მათემატიკის როლი ადამიანის ცხოვრებაში.

რა თქმა უნდა, დამოუკიდებლობა, გადაწყვეტილებების მიღების უნარი, მათზე პასუხისმგებლობა და შეცდომების შიშის არარსებობა ვითარდება არა მხოლოდ ალგებრისა და გეომეტრიის გაკვეთილებზე. მაგრამ ეს დისციპლინები მნიშვნელოვან როლს თამაშობენ პროცესში. მათემატიკა ხელს უწყობს ისეთ თვისებებს, როგორიცაა განსაზღვრა და აქტივობა. მართალია, ბევრი რამ მასწავლებელზეა დამოკიდებული. მასალის არასწორმა წარმოდგენამ, გადაჭარბებულმა სიმკაცრემ და ზეწოლამ, პირიქით, შეიძლება გამოიწვიოს სირთულეებისა და შეცდომების შიში (ჯერ კლასში, შემდეგ კი ცხოვრებაში), აზრის გამოთქმის უხალისობა და პასიურობა.

მათემატიკა ყოველდღიურ ცხოვრებაში

უნივერსიტეტის ან კოლეჯის დამთავრების შემდეგ მოზარდები ყოველდღიურად არ წყვეტენ მათემატიკური ამოცანების ამოხსნას. როგორ დავიჭიროთ მატარებელი? შეიძლება თუ არა ერთი კილოგრამი ხორცი ათი სტუმრისთვის სადილის მომზადება? რამდენი კალორია შეიცავს კერძს? რამდენ ხანს იმუშავებს ერთი ნათურა? ეს და მრავალი სხვა კითხვა პირდაპირ კავშირშია მეცნიერებათა დედოფალთან და მის გარეშე ვერ გადაწყდება. გამოდის, რომ მათემატიკა თითქმის მუდმივად არის ჩვენს ცხოვრებაში უხილავად. და ყველაზე ხშირად ჩვენ ვერც კი ვამჩნევთ ამას.

მათემატიკა საზოგადოებისა და ინდივიდის ცხოვრებაში გავლენას ახდენს უამრავ სფეროზე. ზოგიერთი პროფესია მის გარეშე წარმოუდგენელია, ბევრი გაჩნდა მხოლოდ მისი ცალკეული სფეროების განვითარების წყალობით. თანამედროვე ტექნიკური პროგრესი მჭიდრო კავშირშია მათემატიკური აპარატის გართულებასა და განვითარებასთან. კომპიუტერები და ტელეფონები, თვითმფრინავები და კოსმოსური ხომალდები არასოდეს გამოჩნდებოდნენ, ადამიანებს რომ არ ეცნოთ მეცნიერებათა დედოფალი. თუმცა მათემატიკის როლი ადამიანის ცხოვრებაში ამით არ მთავრდება. მეცნიერება ეხმარება ბავშვს დაეუფლოს სამყაროს, ასწავლის მას უფრო ეფექტურად ურთიერთობას და აყალიბებს მის აზროვნებასა და ინდივიდუალურ ხასიათის თვისებებს. თუმცა, მათემატიკა მარტო ვერ გაუმკლავდება ასეთ პრობლემებს. როგორც ზემოთ აღვნიშნეთ, უზარმაზარ როლს თამაშობს მასალის წარმოდგენა და მისი პიროვნული თვისებები, ვინც აცნობს ბავშვს სამყაროში.

ეფექტური თანამედროვე ვებ დიზაინი არ უნდა იყოს მხოლოდ ლამაზი, მოციმციმე სურათი. ეს უნდა იყოს მარტივი და ინტუიციური. რა საშუალებებით შეიძლება ამის მიღწევა? როგორ ვაგრძნობინო მნახველს ჰარმონიისა და კომფორტის გრძნობა? და აქ მათემატიკა დაგვეხმარება. ახლა ვნახოთ, როგორ მუშაობს მათემატიკის ძირითადი წესები ვებ დიზაინში. ჩვენ ამას განვიხილავთ ოქროს თანაფარდობის წესის, ფიბონაჩის რიცხვების, ხუთი ელემენტის წესის, სინუსური ტალღის რყევების და მესამედების წესის მაგალითის გამოყენებით.

მათემატიკა შესანიშნავია. რიცხვებისა და განტოლებისგან შორს მყოფი ადამიანისთვის ეს შეიძლება აბსურდულად ჟღერდეს. თუმცა, ბევრი ულამაზესი რამ ბუნებაში და თავად სამყაროც მკაცრ მათემატიკურ პროპორციებზეა დაფუძნებული. არისტოტელეც კი, ანტიკურობის ერთ-ერთმა ავტორიტეტულმა ფილოსოფოსმა, თქვა: „მათემატიკა ავლენს წესრიგს, სიმეტრიას და დარწმუნებულობას და ეს არის სილამაზის ყველაზე მნიშვნელოვანი სახეობები“.

საუკუნეების მანძილზე მათემატიკა გამოიყენებოდა როგორც ხელოვნებაში, ასევე არქიტექტურაში. მაგრამ მათემატიკა იშვიათად გამოიყენება ვებსაიტის დიზაინში. ალბათ იმიტომ, რომ გავრცელებულია რწმენა, რომ მათემატიკა და კრეატიულობა შეუთავსებელი საგნებია. მიუხედავად იმისა, რომ ეს მოსაზრება შეიძლება უარყოფილი იყოს, მათემატიკა კარგია ხელსაწყოსაიტების შექმნისას. თუმცა, ამ საკითხში მარტო მათემატიკას არ უნდა დაეყრდნოთ. აქ სხვა რამეა საჭირო.

1. ოქროს თანაფარდობა ან ოქროს მართკუთხედი
ოქროს თანაფარდობა (ოქროს პროპორცია, დაყოფა უკიდურეს და საშუალო თანაფარდობაში) არის უწყვეტი მნიშვნელობის დაყოფა ორ ნაწილად ისეთი თანაფარდობით, რომელშიც უფრო მცირე ნაწილი დაკავშირებულია უფრო დიდთან, როგორც უფრო დიდი მთელ მნიშვნელობასთან. ამ პროპორციის ნაწილების თანაფარდობა გამოიხატება ირაციონალური მათემატიკური მუდმივით, რომელიც უდრის დაახლოებით 1,618033987-ს.

ზოგადად მიღებულია, რომ "ოქროს თანაფარდობის" შემცველ ობიექტებს ადამიანები აღიქვამენ, როგორც ყველაზე ჰარმონიულად. აქ არის საინტერესო ფაქტი ვიკიპედიიდან. ცნობილია, რომ სერგეი ეიზენშტეინმა ხელოვნურად ააგო ფილმი „საბრძოლო ხომალდი პოტემკინი“ ოქროს თანაფარდობის წესების მიხედვით. მან დაარღვია ფირი ხუთ ნაწილად.

პირველ სამში მოქმედება გემზე ხდება. ბოლო ორში - ოდესაში, სადაც აჯანყება ვითარდება. ეს გადასვლა ქალაქში ხდება ზუსტად ოქროს თანაფარდობის წერტილში. და თითოეულ ნაწილს აქვს საკუთარი მოტეხილობა, რომელიც ხდება ოქროს თანაფარდობის კანონის მიხედვით.

ახლა მოდით გადავიდეთ ოქროს ოთხკუთხედზე. აქ ყველაფერი მარტივია. ასეთი მართკუთხედისთვის მიმდებარე გვერდების სიგრძეები კორელაციაშია ოქროს მონაკვეთის წესის მიხედვით, ე.ი. 1:1.618.

ოქროს მართკუთხედის ასაგებად ჯერ დახაზეთ კვადრატი (სურათზე წითელი ფერი), შემდეგ კვადრატის ერთ-ერთი მხარის შუადან მოპირდაპირე კუთხისკენ (ხაზი სურათზე ისრით). ამ ხაზს ვიყენებთ რკალის რადიუსად, რომელიც განსაზღვრავს მართკუთხედის სიმაღლეს. ახლა ჩვენ ვასრულებთ მართკუთხედის დახატვას (ლურჯი ფერი სურათზე).

განვიხილოთ ეს მინიმალისტური დიზაინი ქვემოთ, როგორც ვიზუალური მაგალითი. იგი შედგება 6 ოქროს მართკუთხედისაგან, ზომით 299x185 პიქსელი, ზედიზედ 3 მართკუთხედი. ამ მართკუთხედების გვერდები დაკავშირებულია ოქროს თანაფარდობის წესით 299/185 = 1.616.

დააკვირდით ოქროს მართკუთხედის ირგვლივ დიდ ადგილს. ის ქმნის მშვიდ და სასიამოვნო ატმოსფეროს, რომელშიც ნავიგაციის ელემენტები ადვილად ისუნთქებენ. მიუხედავად რამდენიმე ფერისა და იგივე ტიპის ბლოკების გამოყენებისა, ნავიგაციის ყველა ელემენტი ინტუიციურია და ემსახურება თავის მიზანს.

იმისათვის, რომ დაამატოთ ახალი ბლოკი დიზაინის ლოგიკის დარღვევის გარეშე, ყველაზე მიზანშეწონილია ბლოკების დამატება მესამე სტრიქონში და ქვევით გადაადგილება მსგავსი გზით.

გამოყენების სფეროები.ოქროს მართკუთხედების გამოყენება დიზაინში კარგად შეეფერება სხვადასხვა ფოტო გალერეებს, პორტფელის საიტებს და საიტებს, რომლებიც ორიენტირებულია პროდუქტის პრეზენტაციაზე.

2. ფიბონაჩის რიცხვები დიზაინში
ფიბონაჩის რიცხვები არის რიცხვების მათემატიკური თანმიმდევრობა. განმარტებით, პირველი ორი ფიბონაჩის რიცხვი არის 0 და 1. ყოველი მომდევნო რიცხვი უდრის წინა ორის ჯამს. რიცხვების სერია ასე გამოიყურება: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

ფიბონაჩის რიცხვები გამოიყენება მუსიკაში ინსტრუმენტების დასარეგულირებლად, არქიტექტურაში ჰარმონიული პროპორციების გამოსათვლელად, მაგალითად, ოთახის სიმაღლის თანაფარდობა კედლის გაფორმების სიმაღლეზე სხვადასხვა მასალებით. მცენარის ღეროზე ფოთლებს (ან ტოტებს) შორის მანძილი დაახლოებით ფიბონაჩის რიცხვებთან არის დაკავშირებული.

ფიბონაჩის რიცხვების დიზაინში გამოყენების ძირითადი სფეროა ბლოკების ზომის განსაზღვრა ძირითადი შინაარსით (კონტეინერებით) და გვერდითი ზოლებით. მეთოდის არსი შემდეგია. კონტეინერის ბაზის სიგანე აღებულია, მაგალითად, 90 პიქსელი და თანმიმდევრულად მრავლდება ფიბონაჩის სერიიდან რიცხვებზე. ამ გამოთვლების საფუძველზე აგებულია საიტის ბადე. მოდით შევხედოთ მაგალითს.

გვერდი დაყოფილია სამ სვეტად. კონტეინერის ბაზის სიგანე 90 პიქსელია. მაშინ პირველი სვეტის სიგანეა 180 პიქსელი (90 x 2), მეორე სვეტის სიგანე 270 პიქსელი (90 x 3), ხოლო მესამე სვეტის სიგანე 720 პიქსელი (90 x 8). შრიფტის ზომა ასევე შეესაბამება ფიბონაჩის სერიას. სათაურის შრიფტის ზომაა 55 პიქსელი, განყოფილების შრიფტი 34 პიქსელი და ტექსტის შრიფტი 21 პიქსელი.

თუ საიტს აქვს ფიქსირებული სიგანე, მაგალითად 1000 პიქსელი, მაშინ ფიბონაჩის ნომრები არ არის ძალიან მოსახერხებელი გამოსაყენებლად. ვინაიდან ფიბონაჩის სერიიდან 1000-თან ყველაზე ახლოს არის 987 (..., 610, 987, 1597...), მაშინ სწორედ ამ რიცხვიდან მოგიწევთ გამოთვლების განხორციელება საიტის ბლოკების სიგანეზე. ასეთ სიტუაციებში უმჯობესია გამოიყენოთ ოქროს თანაფარდობის წესი (1000 x 0.618 = 618 px) და გამოიყენოთ იგი ბლოკების სიგანის დასადგენად.

გამოყენების სფეროები.ფიბონაჩის ნომრები საუკეთესოდ შეეფერება ბლოგის დიზაინს და ჟურნალების განლაგებას.

3. ხუთი ელემენტი ან Kundli დიზაინი
მათემატიკის კიდევ ერთი საინტერესო მაგალითი დიზაინში არის ტექნიკა, რომელიც ეფუძნება ინდური კუნდლის ჰოროსკოპის შედგენის წესებს. საფუძველი აქ არის შემდეგი ფიგურა. დახატულია კვადრატი, მის შიგნით ორი დიაგონალი აკავშირებს მოპირდაპირე კუთხეებს, შემდეგ ხაზები აკავშირებს კვადრატის მიმდებარე გვერდების ცენტრებს.

კვადრატის შიგნით ვხედავთ ოთხ ბრილიანტს. ეს არის დიზაინის ხუთი ელემენტის გვერდზე განთავსების საფუძველი.

ქვემოთ მოცემული ვებსაიტის დიზაინის მაგალითი ეფუძნება კუნდლის გეომეტრიას. ეს განლაგება შეიძლება იყოს შესაფერისი ერთგვერდიანი სავიზიტო ბარათის ვებსაიტისთვის jQuery ტექნოლოგიაზე დაფუძნებული ინტერაქტიული დიზაინის ელემენტებით.

ასევე, ეს განლაგება ადვილად შეიძლება გადაიქცეს ვებსაიტად სამსვეტიანი განლაგებით სათაურით და ქვედა კოლონტიტულით.

გამოყენების სფეროები.ეს დიზაინი ყველაზე შესაფერისია პორტფელის საიტებისთვის და საიტებისთვის, რომლებიც ორიენტირებულია პროდუქტების ჩვენებაზე.

4. სინუსოიდური რხევები
თუ გსურთ მრავალფეროვნება, მაშინ სულაც არ არის აუცილებელი ოქროს თანაფარდობისა და ფიბონაჩის ნომრების ძირითადი წესების დაცვა. შეგიძლიათ ექსპერიმენტი სხვა ცნობილი ფორმულებით.

ვნახოთ, როგორ გამოვა ვებსაიტის განლაგება სინუსოიდის რხევების საფუძველზე, მათემატიკური ფუნქცია, რომელიც აღწერს განმეორებით რხევებს. ქვემოთ მოყვანილი სურათი გვიჩვენებს მარტივი და ორიგინალური ერთგვერდიანი ვებსაიტის მაგალითს.

ან სხვა ვარიანტი. განლაგება, რომელიც შედგება სათაურის, ხუთი სვეტისა და ქვედა კოლონტიტულისგან. ასეთი საიტი ასევე შეიძლება გაუმჯობესდეს JQuery ინსტრუმენტებით, რათა ის უფრო ინტერაქტიული გახდეს.

გამოყენების სფეროები.ეს დიზაინი ოპტიმალურია საიტებისთვის, სადაც აუცილებელია მოვლენების ქრონოლოგიის ასახვა. ყველაზე შესაფერისი ჰორიზონტალური ნავიგაციისთვის.

5. მესამედების წესი
ეს წესი ამბობს, რომ სურათი უნდა დაიყოს ცხრა თანაბარ ნაწილად ორი ჰორიზონტალური და ორი ვერტიკალური ხაზით. და ყველა მნიშვნელოვანი კომპოზიციური ელემენტი უნდა განთავსდეს ამ ხაზების გასწვრივ ან მათ კვეთაზე.

ამ მაგალითში ოთხი კვეთიდან ორი შეიცავს ყველაზე მნიშვნელოვან ინფორმაციას. მონიშნულია ვარდისფერი კვადრატებით. და სანავიგაციო ბლოკი მდებარეობს ზუსტად მეორე ჰორიზონტალური ხაზის გასწვრივ.

ზოგჯერ ჩანს, რომ ჩვენი სამყარო მარტივი და გასაგებია. სინამდვილეში, ეს არის სამყაროს დიდი საიდუმლო, რომელმაც შექმნა ასეთი სრულყოფილი პლანეტა. ან იქნებ ის შექმნა ვინმემ, რომელმაც ალბათ იცის რას აკეთებს? ჩვენი დროის უდიდესი გონება ამ საკითხზე მუშაობს.

ყოველ ჯერზე ისინი მიდიან დასკვნამდე, რომ შეუძლებელია შევქმნათ ყველაფერი, რაც გვაქვს უმაღლესი გონების გარეშე. რა არაჩვეულებრივი, რთული და ამავე დროს მარტივი და სპონტანურია ჩვენი პლანეტა დედამიწა! ჩვენს ირგვლივ სამყარო საოცარია თავისი წესებით, ფორმებითა და ფერებით.

ბუნების კანონები

პირველი, რასაც ყურადღება უნდა მიაქციოთ ჩვენს უზარმაზარ და გასაოცარ პლანეტაზე, არის ის, რომ ის გვხვდება მიმდებარე სამყაროს ყველა ფორმაში და ასევე არის სილამაზის, იდეალურობის და პროპორციულობის ძირითადი პრინციპი. ეს სხვა არაფერია, თუ არა მათემატიკა ბუნებაში.

ცნება "სიმეტრია" ნიშნავს ჰარმონიას, სისწორეს. ეს არის გარემომცველი რეალობის თვისება, რომელიც სისტემატიზებს ფრაგმენტებს და აქცევს მათ ერთ მთლიანობად. ჯერ კიდევ ძველ საბერძნეთში, ამ კანონის ნიშნები პირველად გამოჩნდა. მაგალითად, პლატონს სჯეროდა, რომ სილამაზე მხოლოდ სიმეტრიისა და პროპორციულობის შედეგად ჩნდება. სინამდვილეში, თუ შევხედავთ პროპორციულ, სწორ და სრულ ობიექტებს, მაშინ ჩვენი შინაგანი მდგომარეობა მშვენიერი იქნება.

მათემატიკის კანონები ცოცხალ და უსულო ბუნებაში

მოდით შევხედოთ ნებისმიერ არსებას, მაგალითად ყველაზე სრულყოფილს - ადამიანს. ჩვენ დავინახავთ სხეულის სტრუქტურას, რომელიც ორივე მხრიდან ერთნაირად გამოიყურება. თქვენ ასევე შეგიძლიათ ჩამოთვალოთ მრავალი მაგალითი, როგორიცაა მწერები, ცხოველები, საზღვაო ცხოველები, ფრინველები. თითოეულ სახეობას აქვს საკუთარი ფერი.

თუ რაიმე ნიმუში ან დიზაინი არსებობს, ცნობილია, რომ ის ასახულია ცენტრალური ხაზის გარშემო. ყველა ორგანიზმი იქმნება სამყაროს წესების წყალობით. ასეთი მათემატიკური ნიმუშები ასევე შეიძლება ნახოთ უსულო ბუნებაში.

თუ ყურადღებას მიაქცევთ ყველა ფენომენს, როგორიცაა ტორნადო, ცისარტყელა, მცენარეები, ფიფქები, მათში ბევრი საერთო შეგიძლიათ იპოვოთ. ხის შედარებით ფოთოლი გაყოფილია ნახევრად და თითოეული ნაწილი წინას ანარეკლი იქნება.

თუ მაგალითად ავიღოთ ტორნადო, რომელიც ვერტიკალურად ამოდის და ძაბრს ჰგავს, მაშინ ის ასევე შეიძლება დაიყოს ორ აბსოლუტურად იდენტურ ნაწილად. თქვენ შეგიძლიათ იპოვოთ სიმეტრიის ფენომენი დღისა და ღამის, სეზონების ცვლაში. მიმდებარე სამყაროს კანონები ბუნებით მათემატიკაა, რომელსაც აქვს თავისი სრულყოფილი სისტემა. სამყაროს შექმნის მთელი კონცეფცია მასზეა დაფუძნებული.

ცისარტყელა

ჩვენ ხშირად არ ვფიქრობთ ბუნებრივ მოვლენებზე. თოვდა ან წვიმდა, მზე ამოვიდა ან ჭექა-ქუხილი დაარტყა - ამინდის ცვლილების ჩვეულებრივი მდგომარეობა. განვიხილოთ მრავალფერადი რკალი, რომელიც ჩვეულებრივ გვხვდება ნალექის შემდეგ. ცისარტყელა ცაში საოცარი ბუნებრივი მოვლენაა, რომელსაც თან ახლავს ყველა ფერის სპექტრი, რომელიც მხოლოდ ადამიანის თვალით ჩანს. ეს ხდება მზის სხივების გავლის გამო მიმავალ ღრუბელში. წვიმის თითოეული წვეთი ემსახურება როგორც პრიზმას, რომელსაც აქვს ოპტიკური თვისებები. შეიძლება ითქვას, რომ ყოველი წვეთი პატარა ცისარტყელაა.

წყლის ბარიერის გავლით, სხივები იცვლის თავდაპირველ ფერს. სინათლის ყოველ ნაკადს აქვს გარკვეული სიგრძე და ჩრდილი. ამიტომაც ჩვენი თვალები აღიქვამენ ცისარტყელას ასე ფერად. აღვნიშნავთ საინტერესო ფაქტს, რომ ამ ფენომენის დანახვა მხოლოდ ადამიანებს შეუძლიათ. იმიტომ რომ ეს მხოლოდ ილუზიაა.

ცისარტყელის სახეები

1. ყველაზე გავრცელებულია ცისარტყელა მზისგან წარმოქმნილი. ეს არის ყველაზე ნათელი ყველა ჯიშის. შედგება შვიდი ძირითადი ფერისგან: წითელი ნარინჯისფერი, ყვითელი, მწვანე, ლურჯი, ინდიგო, იისფერი. მაგრამ თუ გადავხედავთ დეტალებს, გაცილებით მეტი ჩრდილია, ვიდრე ჩვენი თვალები ხედავენ.
2. მთვარის მიერ შექმნილი ცისარტყელა ღამით ჩნდება. ითვლება, რომ მისი ნახვა ყოველთვის შეიძლება. მაგრამ, როგორც პრაქტიკა გვიჩვენებს, ეს ფენომენი ძირითადად შეინიშნება მხოლოდ წვიმიან ადგილებში ან დიდ ჩანჩქერების მახლობლად. მთვარის ცისარტყელის ფერები ძალიან ბუნდოვანია. ისინი განკუთვნილია მხოლოდ სპეციალური აღჭურვილობის დახმარებით შესამოწმებლად. მაგრამ ამითაც კი, ჩვენს თვალს შეუძლია მხოლოდ თეთრი ზოლის გარჩევა.
3. ცისარტყელა, რომელიც ნისლის შედეგად ჩნდება, შუქის ფართო კაშკაშა თაღს ჰგავს. ზოგჯერ ეს ტიპი აირია წინასთან. ფერი შეიძლება იყოს ნარინჯისფერი ზემოდან და იისფერი ჩრდილის ქვეშ. ნისლში გამავალი მზის სხივები ქმნიან მშვენიერ ბუნებრივ მოვლენას.
4. ძალიან იშვიათად ჩნდება ცაში. ჰორიზონტალური ფორმით იგი არ ჰგავს წინა ტიპებს. ფენომენი შესაძლებელია მხოლოდ ცირუსის ღრუბლების ზემოთ. ისინი ჩვეულებრივ ვრცელდება 8-10 კილომეტრის სიმაღლეზე. კუთხე, რომლითაც ცისარტყელა გამოიჩენს თავს მთელი თავისი დიდებით, უნდა იყოს 58 გრადუსზე მეტი. ფერები ჩვეულებრივ რჩება იგივე, რაც მზის ცისარტყელაში.

ოქროს კოეფიციენტი (1.618)

იდეალური პროპორციულობა ყველაზე ხშირად გვხვდება ცხოველთა სამყაროში. მათ ენიჭებათ პროპორცია, რომელიც უდრის ერთის შესაბამისი PHI რიცხვის ფესვს. ეს თანაფარდობა არის პლანეტის ყველა ცხოველის დამაკავშირებელი ფაქტი. ანტიკურობის დიდმა გონებამ ამ რიცხვს ღვთაებრივი პროპორცია უწოდა. მას ასევე შეიძლება ეწოდოს ოქროს თანაფარდობა.

ეს წესი სრულად შეესაბამება ადამიანის სტრუქტურის ჰარმონიას. მაგალითად, თუ დაადგენთ მანძილს თვალებსა და წარბებს შორის, ეს იქნება ღვთაებრივი მუდმივის ტოლი.

ოქროს თანაფარდობა არის მაგალითი იმისა, თუ რამდენად მნიშვნელოვანია მათემატიკა ბუნებაში, რომლის კანონიც დაიწყეს დიზაინერებმა, მხატვრებმა, არქიტექტორებმა და ლამაზი და სრულყოფილი ნივთების შემქმნელებმა. ისინი ღვთაებრივი მუდმივის დახმარებით ქმნიან თავიანთ ქმნილებებს, რომლებიც გაწონასწორებული, ჰარმონიული და სასიამოვნო შესახედია. ჩვენს გონებას შეუძლია ლამაზად განიხილოს ის ნივთები, საგნები, ფენომენები, სადაც არის ნაწილების არათანაბარი თანაფარდობა. ჩვენი ტვინი ოქროს თანაფარდობას პროპორციულობას უწოდებს.

დნმ სპირალი

როგორც გერმანელმა მეცნიერმა უგო ვეილმა მართებულად აღნიშნა, სიმეტრიის ფესვები მათემატიკიდან გაჩნდა. ბევრი აღნიშნავდა გეომეტრიული ფორმების სრულყოფილებას და ყურადღებას აქცევდა მათ. მაგალითად, თაფლი სხვა არაფერია, თუ არა თავად ბუნების მიერ შექმნილი ექვსკუთხედი. ასევე შეგიძლიათ ყურადღება მიაქციოთ ნაძვის კონუსებს, რომლებსაც ცილინდრული ფორმა აქვთ. სპირალები ასევე ხშირად გვხვდება მიმდებარე სამყაროში: მსხვილი და პატარა პირუტყვის რქები, მოლუსკის ჭურვი, დნმ-ის მოლეკულები.

შექმნილია ოქროს თანაფარდობის პრინციპით. ეს არის დამაკავშირებელი რგოლი მატერიალური სხეულის დიაგრამასა და მის რეალურ გამოსახულებას შორის. და თუ ტვინს გავითვალისწინებთ, ის სხვა არაფერია, თუ არა გამტარი სხეულსა და გონებას შორის. ინტელექტი აკავშირებს სიცოცხლეს და მისი გამოვლინების ფორმას და საშუალებას აძლევს ფორმაში შემავალ სიცოცხლეს საკუთარი თავის შეცნობა. ამის დახმარებით კაცობრიობას შეუძლია გაიგოს მიმდებარე პლანეტა, მოძებნოს მასში შაბლონები, რომლებიც შემდეგ შეიძლება გამოიყენოს შინაგანი სამყაროს შესასწავლად.

დაყოფა ბუნებაში

უჯრედის მიტოზი შედგება ოთხი ეტაპისგან:

• პროფაზა. მასში ბირთვი იზრდება. ჩნდება ქრომოსომები, რომლებიც იწყებენ სპირალურად გადახვევას და ჩვეულ ფორმაში გადაიქცევიან. იქმნება უჯრედის გაყოფის ადგილი. ფაზის ბოლოს, ბირთვი და მისი გარსი იშლება და ქრომოსომა ციტოპლაზმაში მიედინება. ეს გაყოფის ყველაზე გრძელი ეტაპია.
• მეტაფაზა. აქ მთავრდება ქრომოსომების სპირალური მოძრაობა და ისინი ქმნიან მეტაფაზის ფირფიტას. ქრომატიდები განლაგებულია ერთმანეთის საპირისპიროდ დაყოფისთვის. მათ შორის ჩნდება გათიშვის ადგილი - spindle. ამით დასრულდა მეორე ეტაპი.

• ანაფაზა. ქრომატიდები განსხვავდებიან საპირისპირო მიმართულებით. ახლა უჯრედს აქვს ქრომოსომის ორი ნაკრები მათი გაყოფის გამო. ეს ეტაპი ძალიან ხანმოკლეა.
• ტელოფაზა. უჯრედის თითოეულ ნახევარში იქმნება ბირთვი, რომლის ფარგლებშიც იქმნება ბირთვი. ციტოპლაზმა აქტიურად იშლება. ღერო თანდათან ქრება.

მიტოზის მნიშვნელობა

გაყოფის უნიკალური მეთოდის გამო, რეპროდუქციის შემდეგ ყოველ მომდევნო უჯრედს აქვს იგივე გენების შემადგენლობა, როგორც დედას. ორივე უჯრედი იღებს ერთსა და იმავე ქრომოსომულ შემადგენლობას. ეს არ შეიძლებოდა ისეთი მეცნიერების გარეშე, როგორიცაა გეომეტრია. მიტოზის პროგრესირება მნიშვნელოვანია, რადგან ეს არის პრინციპი, რომლითაც ყველა უჯრედი მრავლდება.

საიდან მოდის მუტაციები?

ეს პროცესი უზრუნველყოფს ქრომოსომებისა და გენეტიკური მასალების მუდმივ მიწოდებას თითოეულ უჯრედში. მიტოზის გამო, სხეული ვითარდება, რეპროდუცირება და რეგენერაცია. ზოგიერთი შხამის მოქმედების გამო დარღვევის შემთხვევაში, ქრომოსომა შეიძლება არ გაიყოს ნახევრად, ან შეინიშნოს მათში სტრუქტურული დარღვევები. ეს იქნება საწყისი მუტაციების აშკარა მაჩვენებელი.

შეჯამება

რა საერთო აქვთ მათემატიკასა და ბუნებას? ამ კითხვაზე პასუხს ჩვენს სტატიაში იპოვით. და თუ ჩაღრმავდებით, უნდა თქვათ, რომ ჩვენს ირგვლივ სამყაროს შესწავლით ადამიანი საკუთარ თავს იცნობს. მის გარეშე, რომელმაც ყველა ცოცხალი არსება გააჩინა, არაფერი მოხდებოდა. ბუნება ექსკლუზიურად ჰარმონიაშია, მისი კანონების მკაცრი თანმიმდევრობით. შესაძლებელია თუ არა ეს ყველაფერი მიზეზის გარეშე?

მოვიყვანოთ მეცნიერის, ფილოსოფოსის, მათემატიკოსისა და ფიზიკოსის ანრი პუანკარეს განცხადება, რომელსაც, როგორც სხვას, შეუძლია უპასუხოს კითხვას, არის თუ არა მათემატიკა ბუნებაში ჭეშმარიტად ფუნდამენტური. ზოგიერთ მატერიალისტს შეიძლება არ მოეწონოს ასეთი მსჯელობა, მაგრამ ნაკლებად სავარაუდოა, რომ მათ შეეძლოთ ამის უარყოფა. პუანკარე ამბობს, რომ ჰარმონია, რომლის აღმოჩენაც ადამიანის გონებას სურს ბუნებაში, ვერ იარსებებს მის გარეთ. რომელიც სულ მცირე რამდენიმე ინდივიდის გონებაშია, შეიძლება იყოს ხელმისაწვდომი მთელი კაცობრიობისთვის. კავშირს, რომელიც აერთიანებს გონებრივ აქტივობას, სამყაროს ჰარმონიას უწოდებენ. ბოლო დროს ასეთი პროცესის მიმართ კოლოსალური მიღწევები იყო, მაგრამ ისინი ძალიან მცირეა. სამყაროსა და ინდივიდის დამაკავშირებელი ეს რგოლები ღირებული უნდა იყოს ნებისმიერი ადამიანის გონებისთვის, რომელიც მგრძნობიარეა ამ პროცესების მიმართ.

დასასრულს შევეცდებით მოკლედ დავახასიათოთ მათემატიკის განვითარების ზოგადი ნიმუშები.

1. მათემატიკა არ არის რომელიმე ისტორიული ეპოქის, რომელიმე ხალხის შექმნა; ეს არის მრავალი ეპოქის პროდუქტი, მრავალი თაობის მუშაობის პროდუქტი. წარმოიშვა მისი პირველი ცნებები და დებულებები

როგორც ვნახეთ, ძველ დროში და უკვე ორ ათასზე მეტი წლის წინ ისინი ჰარმონიულ სისტემაში შეიყვანეს. მიუხედავად მათემატიკის ყველა გარდაქმნისა, მისი ცნებები და დასკვნები შენარჩუნებულია, გადადის ერთი ეპოქიდან მეორეში, როგორიცაა, მაგალითად, არითმეტიკის წესები ან პითაგორას თეორემა.

ახალი თეორიები აერთიანებს წინა მიღწევებს, მათ აზუსტებს, ავსებს და განზოგადებს.

ამავდროულად, როგორც ზემოთ მოყვანილი მათემატიკის ისტორიის მოკლე მონახაზიდან ირკვევა, მისი განვითარება არა მხოლოდ ახალი თეორემების უბრალო დაგროვებით ვერ დაიყვანება, არამედ მოიცავს მნიშვნელოვან, თვისობრივ ცვლილებებს. შესაბამისად, მათემატიკის განვითარება იყოფა რამდენიმე პერიოდად, რომელთა შორის გადასვლები ზუსტად მიუთითებს ამ მეცნიერების საგანსა თუ სტრუქტურაში ასეთი ფუნდამენტური ცვლილებებით.

მათემატიკა თავის სფეროში მოიცავს რეალობის რაოდენობრივი ურთიერთობის ყველა ახალ სფეროს. ამავდროულად, მათემატიკის ყველაზე მნიშვნელოვანი საგანი იყო და რჩება სივრცითი ფორმები და რაოდენობრივი ურთიერთობები ამ სიტყვების მარტივი, ყველაზე პირდაპირი გაგებით, და ახალი კავშირებისა და ურთიერთობების მათემატიკური გაგება აუცილებლად ხდება ამის საფუძველზე და მათთან დაკავშირებით. უკვე ჩამოყალიბებული რაოდენობრივი და სივრცითი მეცნიერული ცნებების სისტემა.

და ბოლოს, შედეგების დაგროვება თავად მათემატიკაში აუცილებლად იწვევს როგორც აბსტრაქციის ახალ დონეებზე ასვლას, ასევე ახალ განზოგადებულ ცნებებს, ასევე საფუძვლებისა და საწყისი ცნებების ანალიზში გაღრმავებას.

როგორც მუხა თავისი ძლიერი ზრდით სქელებს ძველ ტოტებს ახალი შრეებით, აგდებს ახალ ტოტებს, იჭიმება ზევით და ღრმავდება ფესვებით ქვევით, ასევე მათემატიკა თავის განვითარებაში აგროვებს ახალ მასალას თავის უკვე ჩამოყალიბებულ ადგილებში, აყალიბებს ახალ მიმართულებებს, აღმას. აბსტრაქციის ახალ სიმაღლეებზე და ღრმავდება მის საფუძვლებში.

2. მათემატიკას აქვს საგანი რეალობის რეალური ფორმები და მიმართებები, მაგრამ, როგორც ენგელსმა თქვა, ამ ფორმებისა და მიმართებების მათი სუფთა სახით შესასწავლად აუცილებელია მათი შინაარსისგან მთლიანად გამოყოფა, ეს უკანასკნელი განზე დავტოვოთ. რაღაც გულგრილი. თუმცა, ფორმები და მიმართებები არ არსებობს შინაარსის მიღმა და მათემატიკური ფორმები და მიმართებები არ შეიძლება იყოს აბსოლუტურად გულგრილი შინაარსის მიმართ. ამიტომ, მათემატიკა, რომელიც თავისი არსით ცდილობს მიაღწიოს ასეთ განცალკევებას, ცდილობს მიაღწიოს შეუძლებელს. ეს არის ფუნდამენტური წინააღმდეგობა მათემატიკის არსში. ეს არის შემეცნების ზოგადი წინააღმდეგობის მათემატიკისთვის დამახასიათებელი გამოვლინება. ყოველი ფენომენის, ყოველი მხარის, რეალობის ყოველი მომენტის ფიქრით ასახვა უხეშია, ამარტივებს მას, ართმევს მას ბუნების საერთო კავშირისგან. როდესაც ადამიანებმა, შეისწავლეს სივრცის თვისებები, დაადგინეს, რომ მას აქვს ევკლიდური გეომეტრია, განსაკუთრებული

შემეცნების მნიშვნელოვანი აქტი, მაგრამ ის ასევე შეიცავდა ილუზიას: სივრცის რეალური თვისებები [აღებულია გამარტივებული, სქემატური გზით, მატერიისგან აბსტრაქციაში. მაგრამ ამის გარეშე უბრალოდ არ იქნებოდა გეომეტრია და სწორედ ამ აბსტრაქციის საფუძველზე (როგორც მისი შიდა კვლევებიდან, ისე მათემატიკური შედეგების ახალ მონაცემებთან სხვა მეცნიერებების შედარებიდან) დაიბადა და გაძლიერდა ახალი გეომეტრიული თეორიები.

ამ წინააღმდეგობის მუდმივი გადაწყვეტა და აღდგენა შემეცნების ეტაპებზე, რომლებიც უფრო ახლოსაა რეალობასთან, წარმოადგენს შემეცნების განვითარების არსს. ამ შემთხვევაში განმსაზღვრელი ფაქტორია, რა თქმა უნდა, ცოდნის დადებითი შინაარსი, მასში აბსოლუტური ჭეშმარიტების ელემენტი. ცოდნა მოძრაობს აღმავალი ხაზის გასწვრივ და არ აღნიშნავს დროს, უბრალოდ შერეულია შეცდომით. ცოდნის მოძრაობა მისი უზუსტობისა და შეზღუდვების მუდმივი დაძლევაა.

ეს მთავარი წინააღმდეგობა იწვევს სხვებს. ჩვენ ეს დავინახეთ დისკრეტული და უწყვეტის საპირისპიროების მაგალითზე. (ბუნებაში მათ შორის აბსოლუტური უფსკრული არ არსებობს და მათემატიკაში მათი განცალკევება აუცილებლად მოჰყვა ახალი ცნებების შექმნის აუცილებლობას, რომლებიც უფრო ღრმად ასახავს რეალობას და ამავე დროს გადალახავს არსებული მათემატიკური თეორიის შინაგან ნაკლოვანებებს). ზუსტად ასევე მათემატიკაში მისი ფუნდამენტური წინააღმდეგობის გამოვლინებად ჩნდება სასრულისა და უსასრულოს, აბსტრაქტულისა და კონკრეტულის, ფორმისა და შინაარსის წინააღმდეგობები და ა.შ. მაგრამ მისი გადამწყვეტი გამოვლინება არის ის, რომ აბსტრაქტული კონკრეტულიდან, ტრიალებს თავისი აბსტრაქტული ცნებების წრეში, ამით მათემატიკა გამოყოფილია ექსპერიმენტისა და პრაქტიკისგან, და ამავე დროს იგი მხოლოდ მეცნიერებაა (ანუ შემეცნებითი ღირებულება) იმდენად, რამდენადაც ემყარება. პრაქტიკაზე, რადგან გამოდის, რომ ეს არ არის სუფთა, არამედ გამოყენებითი მათემატიკა. ჰეგელის ენაზე რომ ვთქვათ, სუფთა მათემატიკა მუდმივად „უარყოფს“ საკუთარ თავს, როგორც წმინდა მათემატიკას, ამის გარეშე მას არ შეუძლია ჰქონდეს მეცნიერული მნიშვნელობა, ვერ განვითარდეს, ვერ გადალახოს ის სირთულეები, რომლებიც აუცილებლად წარმოიქმნება მასში.

მათი ფორმალური ფორმით, მათემატიკური თეორიები ეწინააღმდეგება რეალურ შინაარსს, როგორც კონკრეტული დასკვნების ზოგიერთი სქემა. ამ შემთხვევაში მათემატიკა მოქმედებს როგორც მეთოდი საბუნებისმეტყველო მეცნიერების რაოდენობრივი კანონების ფორმულირებისთვის, როგორც მისი თეორიების განვითარების აპარატი, როგორც ბუნებისმეტყველებისა და ტექნოლოგიების პრობლემების გადაჭრის საშუალება. წმინდა მათემატიკის მნიშვნელობა დღევანდელ ეტაპზე, პირველ რიგში, მათემატიკურ მეთოდშია. და როგორც ყველა მეთოდი არსებობს და ვითარდება არა თავისთავად, არამედ მხოლოდ მისი აპლიკაციების საფუძველზე, იმ შინაარსთან დაკავშირებით, რომელზედაც იგი გამოიყენება, ასევე მათემატიკა ვერ იარსებებს და განვითარდება აპლიკაციების გარეშე. აქ კვლავ ვლინდება დაპირისპირებათა ერთიანობა: ზოგადი მეთოდი ეწინააღმდეგება კონკრეტულ პრობლემას, როგორც მისი გადაჭრის საშუალებას, მაგრამ ის თავად წარმოიქმნება კონკრეტული მასალის განზოგადებიდან და არსებობს.

ვითარდება და თავის გამართლებას მხოლოდ კონკრეტული პრობლემების გადაჭრაში პოულობს.

3. სოციალური პრაქტიკა გადამწყვეტ როლს თამაშობს მათემატიკის განვითარებაში სამი თვალსაზრისით. ის ახალ პრობლემებს უქმნის მათემატიკას, ასტიმულირებს მის განვითარებას ამა თუ იმ მიმართულებით და იძლევა მისი დასკვნების ჭეშმარიტების კრიტერიუმს.

ეს ძალიან ნათლად ჩანს ანალიზის გაჩენაში. პირველ რიგში, ეს იყო მექანიკისა და ტექნოლოგიის განვითარებამ, რამაც გამოიწვია ცვლადების დამოკიდებულების შესწავლის პრობლემა მათი ზოგადი ფორმით. არქიმედე, რომელიც მიუახლოვდა დიფერენციალურ და ინტეგრალურ კალკულუსს, დარჩა, თუმცა, სტატიკური ამოცანების ფარგლებში, ხოლო თანამედროვე დროში მოძრაობის შესწავლამ წარმოშვა ცვლადისა და ფუნქციის ცნებები და აიძულა ანალიზის ფორმულირება. ნიუტონს არ შეეძლო მექანიკის განვითარება შესაბამისი მათემატიკური მეთოდის შემუშავების გარეშე.

მეორეც, სწორედ სოციალური წარმოების საჭიროებებმა აიძულა ყველა ამ პრობლემის ჩამოყალიბება და გადაწყვეტა. არც ძველ და არც შუა საუკუნეების საზოგადოებაში ეს სტიმული არ არსებობდა. დაბოლოს, ძალიან დამახასიათებელია, რომ მათემატიკურმა ანალიზმა თავის დაწყებისას თავისი დასკვნების დასაბუთება სწორედ აპლიკაციებში იპოვა. ეს არის ერთადერთი მიზეზი, რის გამოც იგი შეიძლება განვითარდეს მისი ძირითადი ცნებების (ცვლადი, ფუნქცია, ლიმიტი) იმ მკაცრი განმარტებების გარეშე, რომლებიც მოგვიანებით იქნა მოცემული. ანალიზის სიმართლე დადგინდა მექანიკის, ფიზიკისა და ტექნოლოგიების აპლიკაციებით.

აღნიშნული ეხება მათემატიკის განვითარების ყველა პერიოდს. მე-17 საუკუნიდან. მის განვითარებაზე ყველაზე პირდაპირ გავლენას ახდენს მექანიკასთან ერთად თეორიული ფიზიკა და ახალი ტექნოლოგიების პრობლემები. უწყვეტი მექანიკა, შემდეგ კი ველის თეორია (თერმული გამტარობა, ელექტროენერგია, მაგნეტიზმი, გრავიტაციული ველი) ხელმძღვანელობს ნაწილობრივი დიფერენციალური განტოლებების თეორიის განვითარებას. მოლეკულური თეორიის და ზოგადად სტატისტიკური ფიზიკის განვითარება, გასული საუკუნის ბოლოდან დაწყებული, მნიშვნელოვანი სტიმული იყო ალბათობის თეორიის, განსაკუთრებით კი შემთხვევითი პროცესების თეორიის განვითარებისათვის. ფარდობითობის თეორიამ გადამწყვეტი როლი ითამაშა რიმანის გეომეტრიის განვითარებაში თავისი ანალიტიკური მეთოდებითა და განზოგადებით.

ამჟამად, ახალი მათემატიკური თეორიების განვითარება, როგორიცაა ფუნქციური ანალიზი და ა.შ., სტიმულირებულია კვანტური მექანიკის და ელექტროდინამიკის პრობლემებით, კომპიუტერული ტექნოლოგიების პრობლემებით, ფიზიკისა და ტექნოლოგიების სტატისტიკური საკითხებით და ა.შ. და ა.შ. მათემატიკის ამოცანების ახალი გამოწვევები, უბიძგებს მას კვლევის ახალი საგნებისკენ, მაგრამ ასევე აღვიძებს მათთვის საჭირო მათემატიკის დარგების განვითარებას, რომელიც თავდაპირველად უფრო მეტად განვითარდა საკუთარ თავში, როგორც ეს იყო რიმანის გეომეტრიის შემთხვევაში. მოკლედ, მეცნიერების ინტენსიური განვითარებისთვის აუცილებელია ის არა მხოლოდ ახალი პრობლემების გადაჭრას მიუახლოვდეს, არამედ მათი გადაჭრის აუცილებლობაც დაწესდეს.

საზოგადოების განვითარების საჭიროებები. მათემატიკაში, ახლახან წარმოიშვა მრავალი თეორია, მაგრამ მხოლოდ ისინი არიან განვითარებული და მტკიცედ შედიან მეცნიერებაში, რომლებმაც იპოვეს თავიანთი გამოყენება ბუნებისმეტყველებასა და ტექნოლოგიაში ან შეასრულეს იმ თეორიების მნიშვნელოვანი განზოგადებათა როლი, რომლებსაც აქვთ ასეთი გამოყენება. ამავდროულად, სხვა თეორიები რჩება მოძრაობის გარეშე, როგორიცაა, მაგალითად, ზოგიერთი დახვეწილი გეომეტრიული თეორია (არა-დესარგესიანი, არაარქიმედეს გეომეტრიები), რომლებსაც მნიშვნელოვანი გამოყენება არ ჰქონიათ.

მათემატიკური დასკვნების ჭეშმარიტება საბოლოო საფუძველს პოულობს არა ზოგად განმარტებებსა და აქსიომებში, არა მტკიცებულებების ფორმალურ სიმკაცრეში, არამედ რეალურ გამოყენებაში, ანუ, საბოლოო ჯამში, პრაქტიკაში.

ზოგადად, მათემატიკის განვითარება პირველ რიგში უნდა გავიგოთ, როგორც მისი საგნის ლოგიკის ურთიერთქმედების შედეგი, რომელიც აისახება თავად მათემატიკის შინაგან ლოგიკაში, წარმოების გავლენას და კავშირებს ბუნებისმეტყველებასთან. ეს განსხვავება მიჰყვება წინააღმდეგობებს შორის ბრძოლის რთულ გზებს, მათ შორის მნიშვნელოვანი ცვლილებები მათემატიკის ძირითად შინაარსსა და ფორმებში. შინაარსობრივად მათემატიკის განვითარებას მისი საგანი განსაზღვრავს, მაგრამ მას სტიმულირება უმთავრესად და საბოლოო ჯამში წარმოების მოთხოვნილებებით. ეს არის მათემატიკის განვითარების ძირითადი ნიმუში.

რა თქმა უნდა, არ უნდა დაგვავიწყდეს, რომ ჩვენ ვსაუბრობთ მხოლოდ ძირითად შაბლონზე და რომ მათემატიკასა და წარმოებას შორის კავშირი, ზოგადად, რთულია. რაც ზემოთ ითქვა, ცხადია, რომ გულუბრყვილო იქნებოდა რომელიმე მოცემული მათემატიკური თეორიის გაჩენის პირდაპირი „წარმოების შეკვეთით“ გამართლების მცდელობა. უფრო მეტიც, მათემატიკას, ისევე როგორც ნებისმიერ მეცნიერებას, აქვს შედარებითი დამოუკიდებლობა, საკუთარი შინაგანი ლოგიკა, რომელიც ასახავს, ​​როგორც აღვნიშნეთ, ობიექტურ ლოგიკას, ანუ მისი საგნის კანონზომიერებას.

4. მათემატიკა ყოველთვის განიცდიდა ყველაზე მნიშვნელოვან გავლენას არა მხოლოდ სოციალურ წარმოებაზე, არამედ ზოგადად ყველა სოციალურ მდგომარეობაზე. მისი ბრწყინვალე პროგრესი ძველი საბერძნეთის აღზევების ეპოქაში, ალგებრის წარმატება იტალიაში რენესანსის დროს, ანალიზის განვითარება ინგლისის რევოლუციის შემდგომ ეპოქაში, მათემატიკის წარმატება საფრანგეთში საფრანგეთის რევოლუციის მიმდებარე პერიოდში. - ეს ყველაფერი დამაჯერებლად მეტყველებს მათემატიკის პროგრესის განუყოფელ კავშირზე საზოგადოების ზოგად ტექნიკურ, კულტურულ, პოლიტიკურ პროგრესთან.

ეს ნათლად ჩანს რუსეთში მათემატიკის განვითარებაშიც. დამოუკიდებელი რუსული მათემატიკური სკოლის ჩამოყალიბება, რომელიც მოდის ლობაჩევსკის, ოსტროგრადსკის და ჩებიშევისგან, არ შეიძლება განცალკევდეს მთლიანი რუსული საზოგადოების პროგრესისაგან. ლობაჩევსკის დრო პუშკინის დროა,

გლინკა, დეკაბრისტების დრო და მათემატიკის აყვავება ზოგადი აღმავლობის ერთ-ერთი ელემენტი იყო.

მით უფრო დამაჯერებელია სოციალური განვითარების გავლენა დიდი ოქტომბრის სოციალისტური რევოლუციის შემდგომ პერიოდში, როდესაც ფუნდამენტური მნიშვნელობის კვლევები ერთმანეთის მიყოლებით გაჩნდა საოცარი სისწრაფით მრავალი მიმართულებით: სიმრავლეების თეორიაში, ტოპოლოგიაში, რიცხვთა თეორიაში, ალბათობის თეორიაში, თეორიაში. დიფერენციალური განტოლებები, ფუნქციური ანალიზი, ალგებრა, გეომეტრია.

და ბოლოს, მათემატიკა ყოველთვის იყო და რჩება იდეოლოგიის მნიშვნელოვანი გავლენის ქვეშ. როგორც ნებისმიერ მეცნიერებაში, მათემატიკის ობიექტურ შინაარსს მათემატიკოსები და ფილოსოფოსები ამა თუ იმ იდეოლოგიის ფარგლებში აღიქვამენ და ინტერპრეტირებენ.

მოკლედ, მეცნიერების ობიექტური შინაარსი ყოველთვის ჯდება ამა თუ იმ იდეოლოგიურ ფორმაში; ამ დიალექტიკური დაპირისპირებების - ობიექტური შინაარსისა და იდეოლოგიური ფორმების ერთიანობა და ბრძოლა მათემატიკაში, ისევე როგორც ნებისმიერ მეცნიერებაში, არანაკლებ როლს თამაშობს მის განვითარებაში.

ბრძოლა მატერიალიზმს შორის, რომელიც შეესაბამება მეცნიერების ობიექტურ შინაარსს, და იდეალიზმს, რომელიც ეწინააღმდეგება ამ შინაარსს და ამახინჯებს მის გაგებას, გადის მათემატიკის მთელ ისტორიას. ეს ბრძოლა აშკარად იყო მითითებული უკვე ძველ საბერძნეთში, სადაც პითაგორას, სოკრატეს და პლატონის იდეალიზმი ეწინააღმდეგებოდა თალესის, დემოკრიტეს და სხვა ფილოსოფოსების მატერიალიზმს, რომლებმაც შექმნეს ბერძნული მათემატიკა. მონური სისტემის განვითარებით, საზოგადოების ელიტა ჩამოშორდა წარმოებაში მონაწილეობას, თვლიდა მას ქვედა კლასის ხვედრად და ამან გამოიწვია „სუფთა“ მეცნიერების პრაქტიკისგან გამიჯვნა. მხოლოდ წმინდა თეორიული გეომეტრია იყო აღიარებული ჭეშმარიტი ფილოსოფოსის ყურადღების ღირსად. დამახასიათებელია, რომ პლატონმა მიიჩნია, რომ ზოგიერთი მექანიკური მრუდების და თუნდაც კონუსური მონაკვეთების განვითარებადი კვლევები გეომეტრიის საზღვრებს მიღმა რჩებოდა, რადგან ისინი „არ გვაკავშირებენ მარადიულ და უსხეულო იდეებთან“ და „საჭიროა ვულგარული იარაღების გამოყენება. ხელობა.”

მათემატიკაში მატერიალიზმის იდეალიზმთან ბრძოლის თვალსაჩინო მაგალითია ლობაჩევსკის საქმიანობა, რომელმაც წამოაყენა და დაიცვა მათემატიკის მატერიალისტური გაგება კანტიანიზმის იდეალისტური შეხედულებებისგან.

რუსული მათემატიკური სკოლა ზოგადად მატერიალისტური ტრადიციით ხასიათდება. ამრიგად, ჩებიშევმა ნათლად ხაზი გაუსვა პრაქტიკის გადამწყვეტ მნიშვნელობას, ხოლო ლიაპუნოვმა გამოხატა რუსული მათემატიკური სკოლის სტილი შემდეგი შესანიშნავი სიტყვებით: ”კითხვის დეტალური შემუშავება, რომელიც განსაკუთრებით მნიშვნელოვანია გამოყენების თვალსაზრისით და, ამავე დროს, სპეციალური წარმოდგენით. თეორიული სირთულეები, რომლებიც მოითხოვს ახალი მეთოდების გამოგონებას და მეცნიერების პრინციპებზე ასვლას, შემდეგ დასკვნების განზოგადებას და ამით მეტ-ნაკლებად ზოგადი თეორიის შექმნას. განზოგადება და აბსტრაქცია თავისთავად კი არა, კონკრეტულ მასალასთან არის დაკავშირებული

თეორემები და თეორიები არა თავისთავად, არამედ მეცნიერების ზოგად კავშირში, რაც საბოლოოდ პრაქტიკაში მიგვიყვანს - ეს არის ის, რაც აღმოჩნდება რეალურად მნიშვნელოვანი და პერსპექტიული.

ეს იყო აგრეთვე ისეთი დიდი მეცნიერების მისწრაფებები, როგორებიც იყვნენ გაუსი და რიმანი.

თუმცა, ევროპაში კაპიტალიზმის განვითარებასთან ერთად, მატერიალისტური შეხედულებები, რომლებიც ასახავდნენ მე-16 - მე-19 საუკუნეების მზარდი ბურჟუაზიის მოწინავე იდეოლოგიას, დაიწყო იდეალისტური შეხედულებებით ჩანაცვლება. მაგალითად, კანტორი (1846-1918), როდესაც ქმნიდა უსასრულო სიმრავლეების თეორიას, პირდაპირ მიმართავდა ღმერთს, ლაპარაკობდა იმ სულით, რომ უსასრულო სიმრავლეებს აქვთ აბსოლუტური არსებობა ღვთაებრივ გონებაში. მე-19 საუკუნის ბოლოს და მე-20 საუკუნის დასაწყისის უდიდესი ფრანგი მათემატიკოსი. პუანკარემ წამოაყენა „კონვენციონალიზმის“ იდეალისტური კონცეფცია, რომლის მიხედვითაც მათემატიკა არის ჩვეულებრივი შეთანხმებების სქემა, რომელიც მიღებულია გამოცდილების მრავალფეროვნების აღწერის მოხერხებულობისთვის. ამრიგად, პუანკარეს აზრით, ევკლიდეს გეომეტრიის აქსიომები სხვა არაფერია, თუ არა პირობითი შეთანხმებები და მათი მნიშვნელობა განისაზღვრება მოხერხებულობითა და სიმარტივით, მაგრამ არა მათი შესაბამისობით რეალობასთან. ამიტომ, პუანკარემ თქვა, რომ, მაგალითად, ფიზიკაში ისინი ურჩევნიათ უარი თქვან სინათლის სწორხაზოვანი გავრცელების კანონზე, ვიდრე ევკლიდეს გეომეტრიაზე. ეს თვალსაზრისი უარყო ფარდობითობის თეორიის განვითარებით, რომელიც, მიუხედავად ევკლიდეს გეომეტრიის მთელი „სიმარტივისა“ და „მოხერხებულობისა“, ლობაჩევსკისა და რიმანის მატერიალისტურ იდეებთან სრული თანხმობით, მიგვიყვანა დასკვნამდე, რომ რეალური სივრცის გეომეტრია განსხვავდება ევკლიდესისგან.

სიმრავლეების თეორიაში წარმოქმნილი სირთულეების გამო და მათემატიკის ძირითადი ცნებების ანალიზის საჭიროებასთან დაკავშირებით, მათემატიკოსებს შორის მე-20 საუკუნის დასაწყისში. გაჩნდა სხვადასხვა მიმდინარეობა. დაიკარგა მათემატიკის შინაარსის გაგებაში ერთიანობა; სხვადასხვა მათემატიკოსმა დაიწყო განსხვავებულად ხედვა არა მხოლოდ მეცნიერების ზოგადი საფუძვლების შესახებ, რაც ადრე იყო, არამედ ცალკეული კონკრეტული შედეგებისა და მტკიცებულებების მნიშვნელობისა და მნიშვნელობის განსხვავებულად შეფასებაც კი დაიწყო. დასკვნები, რომლებიც ზოგს აზრიანი და აზრიანი ჩანდა, სხვებმა მნიშვნელობისა და მნიშვნელობის გარეშე გამოაცხადეს. წარმოიშვა „ლოგიკიზმის“, „ინტუიციონიზმის“, „ფორმალიზმის“ იდეალისტური მოძრაობები.

ლოგისტიკოსები ამტკიცებენ, რომ ყველა მათემატიკა გამოდის ლოგიკის ცნებებიდან. ინტუიციონისტები მათემატიკის წყაროს ინტუიციაში ხედავენ და მნიშვნელობას ანიჭებენ მხოლოდ იმას, რაც ინტუიციურად აღიქმება. ამიტომ, კერძოდ, ისინი მთლიანად უარყოფენ კანტორის უსასრულო სიმრავლეების თეორიის მნიშვნელობას. უფრო მეტიც, ინტუიციონისტები უარყოფენ თუნდაც ასეთი განცხადებების მარტივ მნიშვნელობას

როგორც თეორემა, რომ ხარისხის ყველა ალგებრულ განტოლებას აქვს ფესვები. მათთვის ეს განცხადება ცარიელია, სანამ არ იქნება მითითებული ფესვების გამოთვლის მეთოდი. ამრიგად, მათემატიკის ობიექტური მნიშვნელობის სრულ უარყოფამ აიძულა ინტუიციონისტები მათემატიკის მიღწევების მნიშვნელოვანი ნაწილის დისკრედიტაციაზე, როგორც „მნიშვნელობის გარეშე“. მათგან ყველაზე უკიდურესი იქამდე მივიდა, რომ ამტკიცებდა, რომ იმდენი მათემატიკოსია, რამდენი მათემატიკოსია.

თავისებურად ცდილობდა მათემატიკა გადაერჩინა ამ სახის შეტევისგან, ჩვენი საუკუნის დასაწყისის უდიდესმა მათემატიკოსმა - დ.ჰილბერტმა გააკეთა. მისი იდეის არსი იყო მათემატიკური თეორიების დაყვანა სიმბოლოებზე წმინდა ფორმალურ ოპერაციებამდე დადგენილი წესების მიხედვით. გამოთვლა იყო, რომ ასეთი სრულიად ფორმალური მიდგომით მოიხსნებოდა ყველა სირთულე, რადგან მათემატიკის საგანი იქნებოდა სიმბოლოები და მათთან მოქმედების წესები მათ მნიშვნელობასთან ყოველგვარი შეხების გარეშე. ეს არის ფორმალიზმის წყობა მათემატიკაში. ინტუიციონისტი ბროუერის აზრით, ფორმალისტისთვის მათემატიკის ჭეშმარიტება ქაღალდზეა, ხოლო ინტუიციონისტისთვის - მათემატიკოსის თავში.

თუმცა ძნელი არ არის იმის დანახვა, რომ ორივე მათგანი არასწორია, მათემატიკისთვის და ამავე დროს, რაც ქაღალდზე წერია და რასაც მათემატიკოსი ფიქრობს, ასახავს რეალობას და მათემატიკის ჭეშმარიტება მის შესაბამისობაშია ობიექტურ რეალობასთან. . მათემატიკის გამოყოფა მატერიალური რეალობისგან, ყველა ეს ტენდენცია იდეალისტური აღმოჩნდება.

ჰილბერტის იდეა მისმა განვითარებამ დამარცხდა. ავსტრიელმა მათემატიკოსმა გოდელმა დაამტკიცა, რომ არითმეტიკაც კი არ შეიძლება იყოს სრულად ფორმალიზებული, როგორც ჰილბერტი იმედოვნებდა. გოდელის დასკვნამ ნათლად გამოავლინა მათემატიკის შინაგანი დიალექტიკა, რომელიც არ იძლევა მისი რომელიმე სფეროს ფორმალური გაანგარიშებით ამოწურვის საშუალებას. რიცხვების ბუნებრივი რიგის უმარტივესი უსასრულობაც კი აღმოჩნდა სიმბოლოების ამოუწურავი სასრული სქემა და მათთან მუშაობის წესები. ამრიგად, მათემატიკურად დადასტურდა ის, რაც ენგელსმა გამოხატა ზოგადი თვალსაზრისით, როდესაც წერდა:

"უსასრულობა წინააღმდეგობაა... ამ წინააღმდეგობის განადგურება იქნება უსასრულობის დასასრული." ჰილბერტი იმედოვნებდა, რომ მათემატიკური უსასრულობა სასრული სქემების ფარგლებში ჩაერთო და ამით აღმოფხვრა ყველა წინააღმდეგობა და სირთულე. ეს შეუძლებელი აღმოჩნდა.

მაგრამ კაპიტალიზმის პირობებში კონვენციონალიზმი, ინტუიციონიზმი, ფორმალიზმი და სხვა მსგავსი მოძრაობები არა მხოლოდ შენარჩუნებულია, არამედ ავსებენ მათემატიკაზე იდეალისტური შეხედულებების ახალი ვარიანტებით. მათემატიკის საფუძვლების ლოგიკურ ანალიზთან დაკავშირებული თეორიები მნიშვნელოვნად გამოიყენება სუბიექტური იდეალიზმის ზოგიერთ ახალ ვარიანტში. სუბიექტური

იდეალიზმი ახლა იყენებს მათემატიკას, კერძოდ მათემატიკურ ლოგიკას, არანაკლებ ფიზიკას, და ამიტომ განსაკუთრებით მწვავე ხდება მათემატიკის საფუძვლების გაგების საკითხები.

ამრიგად, მათემატიკის განვითარების სირთულეებმა კაპიტალიზმის პირობებში წარმოშვა ამ მეცნიერების იდეოლოგიური კრიზისი, თავისი საფუძვლებით ფიზიკის კრიზისის მსგავსი, რომლის არსი განმარტა ლენინმა თავის ბრწყინვალე ნაშრომში „მატერიალიზმი და ემპირიო“. -კრიტიკა. ეს კრიზისი სულაც არ ნიშნავს იმას, რომ კაპიტალისტურ ქვეყნებში მათემატიკა სრულიად ჩამორჩენილია მის განვითარებაში. აშკარად იდეალისტური პოზიციების მქონე მეცნიერთა რიცხვი მნიშვნელოვან, ზოგჯერ გამორჩეულ წარმატებებს აღწევს კონკრეტული მათემატიკური ამოცანების გადაჭრასა და ახალი თეორიების შემუშავებაში. საკმარისია მივმართოთ მათემატიკური ლოგიკის ბრწყინვალე განვითარებას.

კაპიტალისტურ ქვეყნებში ფართოდ გავრცელებული მათემატიკის ხედვის ფუნდამენტური ნაკლი მდგომარეობს მის იდეალიზმსა და მეტაფიზიკაში: მათემატიკის რეალობისგან გამიჯვნა და მისი რეალური განვითარების უგულებელყოფა. ლოგისტიკა, ინტუიციონიზმი, ფორმალიზმი და სხვა მსგავსი ტენდენციები ხაზს უსვამს მათემატიკაში მის ერთ-ერთ ასპექტს - ლოგიკასთან კავშირს, ინტუიციურ სიცხადეს, ფორმალურ სიმკაცრეს და ა.შ. თავისთავად მათემატიკის ერთ-ერთი თვისება არის მთლიანად მათემატიკის მხედველობის დაკარგვა. სწორედ ამ ცალმხრივობის გამო ვერც ერთ ამ მიმდინარეობას, ცალკეული დასკვნების მთელი დახვეწილობისა და სიღრმის გამო, არ შეუძლია მათემატიკის სწორ გაგებამდე მიყვანა. იდეალიზმისა და მეტაფიზიკის სხვადასხვა მიმდინარეობებისა და ჩრდილებისგან განსხვავებით, დიალექტიკური მატერიალიზმი განიხილავს მათემატიკას, ისევე როგორც მთელ მეცნიერებას, როგორც ეს არის, მისი კავშირებისა და განვითარების მთელი სიმდიდრითა და სირთულეებით. და სწორედ იმიტომ, რომ დიალექტიკური მატერიალიზმი ცდილობს გაიგოს მეცნიერებასა და რეალობას შორის კავშირების მთელი სიმდიდრე და სირთულე, მისი განვითარების მთელი სირთულე, გამოცდილების მარტივი განზოგადებადან უფრო მაღალ აბსტრაქციებამდე და მათგან პრაქტიკაში, ზუსტად იმიტომ, რომ ის მუდმივად მეცნიერებისადმი თავის მიდგომას ობიექტური შინაარსის შესაბამისად, თავისი ახალი აღმოჩენებით, სწორედ ამ მიზეზით და, საბოლოო ჯამში, მხოლოდ ამ მიზეზით აღმოჩნდება, რომ ის არის ერთადერთი ჭეშმარიტად მეცნიერული ფილოსოფია, რომელიც მიგვიყვანს მეცნიერების სწორ გაგებამდე. ზოგადად და, კერძოდ, მათემატიკა.