Termins (modulis) burtiskā tulkojumā no latīņu valodas nozīmē "mērīt". Šo jēdzienu matemātikā ieviesa angļu zinātnieks R. Kotss. Un vācu matemātiķis K. Weierstrass ieviesa moduļa zīmi - simbolu, ar kuru šis jēdziens tiek apzīmēts rakstot.

Saskarsmē ar

Pirmo reizi šis jēdziens tiek apgūts matemātikā vidusskolas 6. klases programmā. Saskaņā ar vienu definīciju modulis ir reāla skaitļa absolūtā vērtība. Citiem vārdiem sakot, lai uzzinātu reālā skaitļa moduli, jums ir jāatmet tā zīme.

Grafiski absolūtā vērtība a apzīmēts kā |a|.

Šīs koncepcijas galvenā atšķirīgā iezīme ir tā, ka tā vienmēr ir nenegatīva vērtība.

Skaitļus, kas atšķiras viens no otra tikai ar zīmi, sauc par pretējiem skaitļiem. Ja vērtība ir pozitīva, tad tās pretstats ir negatīvs, un nulle ir paša pretstats.

ģeometriskā vērtība

Ja aplūkosim moduļa jēdzienu no ģeometrijas viedokļa, tad tas apzīmē attālumu, ko mēra vienības segmentos no sākuma līdz dots punkts. Šī definīcija pilnībā atklāj pētāmā termina ģeometrisko nozīmi.

Grafiski to var izteikt šādi: |a| = O.A.

Absolūtās vērtības īpašības

Tālāk mēs apsvērsim visas šī jēdziena matemātiskās īpašības un rakstīšanas veidus burtisku izteiksmju veidā:

Vienādojumu risināšanas ar moduli iezīmes

Ja mēs runājam par matemātisko vienādojumu un nevienādību risināšanu, kas satur moduli, tad jums jāatceras, ka, lai tos atrisinātu, jums būs jāatver šī zīme.

Piemēram, ja absolūtās vērtības zīme satur kādu matemātisku izteiksmi, tad pirms moduļa atvēršanas ir jāņem vērā pašreizējās matemātiskās definīcijas.

|A + 5| = A + 5 ja A ir lielāka vai vienāda ar nulli.

5-A ja A ir mazāks par nulli.

Dažos gadījumos zīmi var nepārprotami paplašināt jebkurai mainīgā vērtībai.

Apskatīsim vēl vienu piemēru. Konstruēsim koordinātu līniju, uz kuras atzīmējam visas skaitliskās vērtības, kuru absolūtā vērtība būs 5.

Vispirms jānozīmē koordinātu līnija, jānorāda uz tās koordinātu izcelsme un jāiestata viena segmenta lielums. Turklāt līnijai jābūt virzienam. Tagad uz šīs taisnes ir jāpiemēro marķējumi, kas būs vienādi ar viena segmenta vērtību.

Tādējādi mēs varam redzēt, ka uz šīs koordinātu līnijas būs divi mūs interesējoši punkti ar vērtībām 5 un -5.

MBOU vidusskola №17 Ivanovs

« Modulo vienādojumi»
Metodiskā izstrāde

Sastādīts

matemātikas skolotājs

Ļebedeva N.V.

20010. gads

Paskaidrojuma piezīme

1. nodaļa Ievads

2. sadaļa. Galvenās iezīmes 3. sadaļa. Skaitļa moduļa jēdziena ģeometriskā interpretācija 4. sadaļa. Funkcijas y = |x| grafiks 5. sadaļa Konvencijas

2. nodaļa

1. sadaļa. Formas |F(х)| vienādojumi = m (vienšūņi) 2. sadaļa. Formas vienādojumi F(|х|) = m 3. sadaļa. Formas |F(х)| vienādojumi = G(x) 4. sadaļa. Formas |F(х)| vienādojumi = ± F(x) (skaista) 5. sadaļa. Formas |F(х)| vienādojumi = |G(x)| 6. sadaļa. Nestandarta vienādojumu risināšanas piemēri 7. sadaļa. Formas |F(х)| vienādojumi + |G(x)| = 0 8. sadaļa. Formas |а 1 x ± в 1 | vienādojumi ± |a 2 x ± in 2 | ± …|a n x ± n | = m 9. sadaļa. Vienādojumi, kas satur vairākus moduļus

3. nodaļa. Dažādu vienādojumu risināšanas piemēri ar moduli.

1. sadaļa. Trigonometriskie vienādojumi 2. sadaļa. Eksponenciālie vienādojumi 3. sadaļa. Logaritmiskie vienādojumi 4. sadaļa. Iracionālie vienādojumi 5. sadaļa. Augstas sarežģītības uzdevumi Atbildes uz vingrinājumiem Bibliogrāfija

Paskaidrojuma piezīme.

Reālā skaitļa absolūtās vērtības (moduļa) jēdziens ir viens no tā būtiskajiem raksturlielumiem. Šo jēdzienu plaši izmanto dažādās fizisko, matemātikas un tehnisko zinātņu nozarēs. Matemātikas kursa mācīšanas praksē in vidusskola saskaņā ar Krievijas Federācijas Aizsardzības ministrijas programmu jēdziens "skaitļa absolūtā vērtība" parādās atkārtoti: 6. klasē tiek ieviesta moduļa definīcija, tā ģeometriskā nozīme; 8.klasē tiek veidots absolūtās kļūdas jēdziens, apskatīts vienkāršāko moduli saturošo vienādojumu un nevienādību risinājums, pētītas aritmētiskās kvadrātsaknes īpašības; 11. klasē jēdziens atrodams sadaļā “Sakne ngrāds." Mācību pieredze rāda, ka studenti bieži saskaras ar grūtībām, risinot uzdevumus, kuros ir nepieciešamas zināšanas par šo materiālu, un bieži vien izlaiž, pirms sāk pildīt. Eksāmenu uzdevumu tekstos 9. un 11. klašu kursam ir iekļauti arī līdzīgi uzdevumi. Turklāt prasības, ko augstskolas izvirza skolu absolventiem, ir atšķirīgas, proti, augstāka līmeņa nekā skolas mācību programmas prasības. Dzīvei mūsdienu sabiedrībā ir ļoti svarīgi veidot matemātisko domāšanas stilu, kas izpaužas noteiktās garīgās prasmēs. Moduļu problēmu risināšanas procesā ir nepieciešama prasme pielietot tādas metodes kā vispārināšana un konkretizācija, analīze, klasifikācija un sistematizācija, analoģijas. Šādu uzdevumu risinājums ļauj pārbaudīt zināšanas par skolas kursa galvenajām sadaļām, loģiskās domāšanas līmeni un sākotnējās pētniecības prasmes. Šis darbs ir veltīts vienai no sadaļām - moduli saturošu vienādojumu risināšanai. Tas sastāv no trim nodaļām. Pirmajā nodaļā ir izklāstīti pamatjēdzieni un svarīgākie teorētiskie aprēķini. Otrajā nodaļā ir piedāvāti deviņi pamata vienādojumu veidi, kas satur moduli, apskatītas to risināšanas metodes un analizēti dažādu sarežģītības līmeņu piemēri. Trešā nodaļa piedāvā sarežģītākus un nestandarta vienādojumus (trigonometriskos, eksponenciālos, logaritmiskos un iracionālos). Katram vienādojumu veidam ir paredzēti vingrinājumi neatkarīgs lēmums(atbildes un instrukcijas pievienotas). Šī darba galvenais mērķis ir sniegt metodisko palīdzību skolotājiem mācību stundu sagatavošanā un izvēles kursu organizēšanā. Materiālu var izmantot arī kā mācību rokasgrāmata vidusskolēniem. Darbā piedāvātie uzdevumi ir interesanti un ne vienmēr viegli risināmi, kas ļauj padarīt apzinātāku studentu mācību motivāciju, pārbaudīt viņu spējas, uzlabot skolu absolventu sagatavotības līmeni iestājai augstskolās. Diferencēta piedāvāto vingrinājumu atlase nozīmē pāreju no materiāla asimilācijas reproduktīvā līmeņa uz radošo, kā arī iespēju iemācīt pielietot savas zināšanas nestandarta problēmu risināšanā.

1. nodaļa. Ievads.

1. sadaļa. Absolūtās vērtības noteikšana .

Definīcija : Reāla skaitļa absolūtā vērtība (modulis). a sauc par nenegatīvu skaitli: a vai -a. Apzīmējums: │ a │ Ieraksts skan šādi: "skaitļa a modulis" vai "skaitļa a absolūtā vērtība"

│ a ja a > 0

│a│ = │ 0, ja a = 0 (1)

│ - a, ja a
Piemēri: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Izvērst izteiksmes moduli:

a) │x - 8│ ja x > 12 b) │2x + 3│ ja x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

2. sadaļa. Pamatīpašības.

Apsveriet absolūtās vērtības pamatīpašības. Īpašums Nr. 1: Pretējiem skaitļiem ir vienādi moduļi, t.i. │а│=│-а│ Parādīsim vienlīdzības pareizību. Pierakstīsim skaitļa definīciju - a : │- a│= (2) Salīdzināsim kopas (1) un (2). Acīmredzot skaitļu absolūto vērtību definīcijas a un - a atbilst. Sekojoši, │а│=│-а│
Apsverot tālāk norādītās īpašības, mēs aprobežojamies ar to formulējumu, jo to pierādījumi ir doti Īpašums Nr. 2: Galīga skaitļa summas absolūtā vērtība reāli skaitļi nepārsniedz terminu absolūto vērtību summu: │a 1 + a 2 +…+ a n Īpašums Nr. 3: Absolūtā starpības vērtība starp diviem reāliem skaitļiem nepārsniedz to absolūto vērtību summu: │а - в│ ≤│а│+│в│ Īpašums Nr. 4: Galīga reālu skaitļu reizinājuma absolūtā vērtība ir vienāda ar faktoru absolūto vērtību reizinājumu: │а · в│=│а│·│в│ Īpašums Nr. 5: Reālo skaitļu koeficienta absolūtā vērtība ir vienāda ar to absolūto vērtību koeficientu:

3. sadaļa. Skaitļa moduļa jēdziena ģeometriskā interpretācija.

Katru reālo skaitli var saistīt ar punktu uz skaitļu līnijas, kas būs šī reālā skaitļa ģeometrisks attēlojums. Katrs skaitļu līnijas punkts atbilst tā attālumam no sākuma, t.i. segmenta garums no sākuma līdz dotajam punktam. Šis attālums vienmēr tiek uzskatīts par nenegatīvu vērtību. Tāpēc atbilstošā segmenta garums būs dotā reālā skaitļa absolūtās vērtības ģeometriskā interpretācija

Prezentēts ģeometriskā ilustrācija nepārprotami apliecina īpašumu Nr.1, t.i. pretējo skaitļu moduļi ir vienādi. No šejienes vienlīdzības derīgums ir viegli saprotams: │x - a│= │a - x│. Acīmredzamāk kļūst arī atrisināt vienādojumu │х│= m, kur m ≥ 0, proti, x 1,2 = ± m. Piemēri: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; četri

4. sadaļa. Funkcijas y \u003d │х│ grafiks

Šīs funkcijas domēns ir visi reālie skaitļi.

5. sadaļa. Simboli.

Nākotnē, apsverot vienādojumu risināšanas piemērus, tiks izmantotas šādas konvencijas: ( - sistēmas zīme [ - iestatīt zīmi Risinot vienādojumu (vienādību) sistēmu, tiek atrasts sistēmā ietverto vienādojumu (nevienādību) atrisinājumu krustpunkts. Risinot vienādojumu (vienādību) kopu, tiek atrasta kopā iekļauto vienādojumu (vienādību) atrisinājumu savienība.

2. nodaļa

Šajā nodaļā mēs apskatīsim algebriskos veidus, kā atrisināt vienādojumus, kas satur vienu vai vairākus moduļus.

1. sadaļa. Formas vienādojumi │F (х) │= m

Šāda veida vienādojumu sauc par vienkāršāko. Tam ir risinājums tad un tikai tad, ja m ≥ 0. Pēc moduļa definīcijas sākotnējais vienādojums ir līdzvērtīgs divu vienādojumu kombinācijai: │ F(x)│=m
Piemēri:
№1. Atrisiniet vienādojumu: │7x - 2│= 9


Atbilde: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 = 0; x 2 = -3 Atbilde: sakņu summa ir - 2.№3
│x 4 -5x 2 + 2│ = 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 apzīmē x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – abas vērtības apmierina nosacījumu m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Atbilde: vienādojuma 7 sakņu skaits. Vingrinājumi:
№1. Atrisiniet vienādojumu un norādiet sakņu summu: │x - 5│= 3 №2 . Atrisiniet vienādojumu un norādiet mazāko sakni: │x 2 + x │ \u003d 0 №3 . Atrisiniet vienādojumu un norādiet lielāko sakni: │x 2 - 5x + 4 │ \u003d 4 №4 .Atrisiniet vienādojumu un norādiet visu sakni: │2x 2 - 7x + 6│ \u003d 1 №5 .Atrisiniet vienādojumu un norādiet sakņu skaitu: │x 4 - 13x 2 + 50 │ = 14

2. sadaļa. Formas vienādojumi F(│х│) = m

Funkcijas arguments kreisajā pusē atrodas zem moduļa zīmes, bet labā puse ir neatkarīga no mainīgā. Apskatīsim divus šāda veida vienādojumu risināšanas veidus. 1 ceļš: Pēc absolūtās vērtības definīcijas sākotnējais vienādojums ir līdzvērtīgs divu sistēmu kopumam. Katrā no tiem apakšmoduļa izteiksmei tiek uzlikts nosacījums. F(│х│) =m
Tā kā funkcija F(│х│) ir pat visā definīcijas jomā, vienādojumu F(х) = m un F(-х) = m saknes ir pretēju skaitļu pāri. Tāpēc pietiek atrisināt kādu no sistēmām (šādi aplūkojot piemērus, tiks dots vienas sistēmas risinājums). 2 ceļi: Jauna mainīgā ieviešanas metodes pielietojums. Šajā gadījumā tiek ieviests apzīmējums │х│= a, kur a ≥ 0. Šī metode mazāk apjomīgs dizainā.
Piemēri: №1 . Atrisiniet vienādojumu: 3x 2 - 4│x│ = - 1 Izmantosim jauna mainīgā ievadīšanu. Apzīmē │x│= a, kur a ≥ 0. Iegūstam vienādojumu 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Mēs atgriežamies pie sākotnējā mainīgā: │x │ = 1 un │х│ = 1/3. Katram vienādojumam ir divas saknes. Atbilde: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Atrisiniet vienādojumu: 5x 2 + 3│x│- 1 \u003d 1/2 │x│ + 3x 2
Atradīsim pirmās kopas sistēmas risinājumu: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Ņemiet vērā, ka x 2 ir neizpilda nosacījumu x ≥ 0. Pēc risinājuma otrā sistēma būs pretējs skaitlis x 1 . Atbilde: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Atrisiniet vienādojumu: x 4 - │х│= 0 Apzīmējiet │х│= a, kur a ≥ 0. Iegūstam vienādojumu a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d a 2 \u003d 1 Mēs atgriežamies pie sākotnējā mainīgā: │х│=0 un │х│= 1 x = 0; ± 1 Atbilde: x 1 = 0; X 2 = 1; X 3 = - 1.
Vingrinājumi: №6. Atrisiniet vienādojumu: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Atrisiniet vienādojumu, atbildē norādiet sakņu skaitu: 3x 2 - 7│x│ + 2 = 0 №8 . Atrisiniet vienādojumu, atbildē norādiet risinājumus: x 4 + │х│ - 2 = 0

3. sadaļa. Formas vienādojumi │F(х)│ = G(х)

Šāda veida vienādojuma labā puse ir atkarīga no mainīgā, un tāpēc tai ir risinājums tad un tikai tad, ja labā puse ir funkcija G(x) ≥ 0. Sākotnējo vienādojumu var atrisināt divos veidos: 1 ceļš: Standarts, kas balstīts uz moduļa izpaušanu, pamatojoties uz tā definīciju, un sastāv no līdzvērtīgas pārejas uz divu sistēmu kombināciju. │ F(x)│ =G(X)

Šo metodi ir racionāli izmantot, ja funkcijai G(x) ir sarežģīta izteiksme, bet funkcijai F(x) ir mazāk sarežģīta izteiksme, jo tai ir jāatrisina nevienādības ar funkciju F(x). 2 ceļi: Tas sastāv no pārejas uz līdzvērtīgu sistēmu, kurā nosacījums tiek uzlikts labajā pusē. │ F(x)│= G(x)

Šo metodi ērtāk izmantot, ja funkcijas G(x) izteiksme ir mazāk sarežģīta nekā funkcijai F(x), jo tiek pieņemts nevienādības G(x) atrisinājums ≥ 0. Turklāt gadījumā no vairākiem moduļiem, šī metode ir ieteicama, lai izmantotu otro iespēju. Piemēri: №1. Atrisiniet vienādojumu: │x + 2│= 6 -2x
(vienā virzienā) Atbilde: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(divvirzienu) Atbilde: sakņu reizinājums ir 3.
№3. Atrisiniet vienādojumu, atbildē ierakstiet sakņu summu:
│x - 6 │ \u003d x 2 - 5x + 9

Atbilde: sakņu summa ir 4.
Vingrinājumi: №9. │x + 4│= - 3x №10. Atrisiniet vienādojumu, atbildē norādiet risinājumu skaitu: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Atrisiniet vienādojumu, atbildē norādiet sakņu reizinājumu: │x + 3 │ \u003d x 2 + x - 6

4. sadaļa. Formas vienādojumi │F(x)│= F(x) un │F(x)│= - F(x)

Šāda veida vienādojumus dažreiz sauc par "skaistajiem". Tā kā vienādojumu labā puse ir atkarīga no mainīgā, risinājumi pastāv tad un tikai tad, ja labā puse nav negatīva. Tāpēc sākotnējie vienādojumi ir līdzvērtīgi nevienādībām:
│F(x)│= F(x) F(x) ≥ 0 un │F(x)│= - F(x) F(x) Piemēri: №1 . Atrisiniet vienādojumu, atbildē norādiet mazākā veselā skaitļa sakni: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Atbilde: x = 1№2. Atrisiniet vienādojumu, atbildē norādiet atstarpes garumu: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Atbilde: atstarpes garums ir 6.№3 . Atrisiniet vienādojumu, atbildē norādiet veselu atrisinājumu skaitu: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Atbilde: 4 veseli risinājumi.№4 . Atrisiniet vienādojumu, atbildē norādiet lielāko sakni:
│4 – x 
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Atbilde: x = 3.

Vingrinājumi: №12. Atrisiniet vienādojumu, atbildē norādiet visu sakni: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Atrisiniet vienādojumu, atbildē norādiet veselo skaitļu atrisinājumu skaitu: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Atrisiniet vienādojumu, atbildē norādiet veselu skaitli, kas nav vienādojuma sakne:

5. sadaļa. Formas vienādojumi │F(x)│= │G(x)│

Tā kā abas vienādojuma puses nav negatīvas, risinājums ietver divu gadījumu izskatīšanu: submodulāras izteiksmes ir vienādas vai pretējas pēc zīmes. Tāpēc sākotnējais vienādojums ir līdzvērtīgs divu vienādojumu kombinācijai: │ F(x)│= │ G(x)│
Piemēri: №1. Atrisiniet vienādojumu, atbildē norādiet visu sakni: │x + 3│ \u003d │2x - 1│
Atbilde: vesela skaitļa sakne x = 4.№2. Atrisiniet vienādojumu: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Atbilde: x = 2.№3 . Atrisiniet vienādojumu, atbildē norādiet sakņu reizinājumu:




Vienādojuma saknes 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Atbilde: sakņu reizinājums ir 0,25. Vingrinājumi: №15 . Atrisiniet vienādojumu, atbildē norādiet visu risinājumu: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Atrisiniet vienādojumu, atbildē norādiet mazāko sakni: │5x - 3│=│7 - x│ №17 . Atrisiniet vienādojumu, atbildē ierakstiet sakņu summu:

6. sadaļa. Nestandarta vienādojumu risināšanas piemēri

Šajā sadaļā mēs aplūkojam nestandarta vienādojumu piemērus, kuru risinājumā izteiksmes absolūtā vērtība tiek atklāta pēc definīcijas. Piemēri:

№1. Atrisiniet vienādojumu, atbildē norādiet sakņu summu: x │x│- 5x - 6 \u003d 0
Atbilde: sakņu summa ir 1 №2. . Atrisiniet vienādojumu, atbildē norādiet mazāko sakni: x 2 - 4x
- 5 = 0
Atbilde: mazāka sakne x = - 5. №3. Atrisiniet vienādojumu:

Atbilde: x = -1. Vingrinājumi: №18. Atrisiniet vienādojumu un uzrakstiet sakņu summu: x │3x + 5│= 3x 2 + 4x + 3
№19. Atrisiniet vienādojumu: x 2 - 3x \u003d

№20. Atrisiniet vienādojumu:

7. sadaļa. Vienādojumi formā │F(x)│+│G(x)│=0

Ir viegli redzēt, ka šāda veida vienādojuma kreisajā pusē ir nenegatīvu lielumu summa. Tāpēc sākotnējam vienādojumam ir risinājums tad un tikai tad, ja abi termini vienlaikus ir vienādi ar nulli. Vienādojums ir līdzvērtīgs vienādojumu sistēmai: │ F(x)│+│ G(x)│=0
Piemēri: №1 . Atrisiniet vienādojumu:
Atbilde: x = 2. №2. Atrisiniet vienādojumu: Atbilde: x = 1. Vingrinājumi: №21. Atrisiniet vienādojumu: №22 . Atrisiniet vienādojumu, atbildē ierakstiet sakņu summu: №23 . Atrisiniet vienādojumu, atbildē norādiet risinājumu skaitu:

8. sadaļa. Formas vienādojumi

Lai atrisinātu šāda veida vienādojumus, tiek izmantota intervālu metode. Ja tas tiek atrisināts ar moduļu secīgu paplašināšanu, tad mēs iegūstam n sistēmu komplektiem, kas ir ļoti apgrūtinoši un neērti. Apsveriet intervālu metodes algoritmu: 1). Atrodiet mainīgās vērtības X, kuram katrs modulis ir vienāds ar nulli (apakšmoduļu izteiksmju nulles):
2). Atrastās vērtības ir atzīmētas uz skaitļu līnijas, kas ir sadalīta intervālos (intervālu skaits attiecīgi ir vienāds ar n+1 ) 3). Nosakiet, ar kādu zīmi katrs modulis tiek atklāts katrā no iegūtajiem intervāliem (izgatavojot risinājumu, var izmantot skaitļa līniju, atzīmējot uz tās zīmes) 4). Sākotnējais vienādojums ir līdzvērtīgs kopai n+1 sistēmas, katrā no kurām norādīta mainīgā piederība X viens no intervāliem. Piemēri: №1 . Atrisiniet vienādojumu, atbildē norādiet lielāko sakni:
viens). Atradīsim apakšmoduļu izteiksmju nulles: x = 2; x = -3 2). Mēs atzīmējam atrastās vērtības uz skaitļu līnijas un nosakām, ar kādu zīmi katrs modulis tiek atklāts iegūtajos intervālos:
x – 2 x – 2 x – 2 – + - 3 2 x 2 x + 6 2 x + 6 2 x + 6 - + + 3)
- nav risinājumu Vienādojumam ir divas saknes. Atbilde: lielākā sakne ir x = 2. №2. Atrisiniet vienādojumu, atbildē ierakstiet visu sakni:
viens). Atradīsim apakšmoduļu izteiksmju nulles: x = 1,5; x = - 1 2). Mēs atzīmējam atrastās vērtības uz skaitļu līnijas un nosaka, ar kādu zīmi katrs modulis tiek atklāts iegūtajos intervālos: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х - 3 2х - 3 2х - 3 - - +
3).
Pēdējai sistēmai nav atrisinājumu, tāpēc vienādojumam ir divas saknes. Atrisinot vienādojumu, jāpievērš uzmanība zīmei “-” otrā moduļa priekšā. Atbilde: vesela skaitļa sakne x = 7. №3. Atrisiniet vienādojumu, atbildē norādiet sakņu summu: 1). Atradīsim apakšmoduļu izteiksmju nulles: x = 5; x = 1; x = - 2 2). Mēs atzīmējam atrastās vērtības uz skaitļu līnijas un nosaka, ar kādu zīmi katrs modulis tiek atklāts iegūtajos intervālos: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Vienādojumam ir divas saknes x = 0 un 2. Atbilde: sakņu summa ir 2. №4 . Atrisiniet vienādojumu: 1). Atradīsim apakšmoduļu izteiksmju nulles: x = 1; x = 2; x = 3. 2). Nosakīsim zīmi, ar kuru katrs modulis tiek paplašināts iegūtajos intervālos. 3).
Apvienosim pirmā risinājumus trīs sistēmas. Atbilde: ; x = 5.
Vingrinājumi: №24. Atrisiniet vienādojumu:
№25. Atrisiniet vienādojumu, atbildē ierakstiet sakņu summu: №26. Atrisiniet vienādojumu, atbildē norādiet mazāko sakni: №27. Atrisiniet vienādojumu, atbildē norādiet lielāko sakni:

9. sadaļa. Vienādojumi, kas satur vairākus moduļus

Vienādojumi, kas satur vairākus moduļus, pieņem absolūtās vērtības apakšmoduļu izteiksmēs. Šāda veida vienādojumu risināšanas pamatprincips ir moduļu secīga atklāšana, sākot ar "ārējo". Risinājuma gaitā tiek izmantotas sadaļās Nr.1, Nr.3 aplūkotās tehnikas.

Piemēri: №1. Atrisiniet vienādojumu:
Atbilde: x = 1; - vienpadsmit. №2. Atrisiniet vienādojumu:
Atbilde: x = 0; četri; - četras. №3. Atrisiniet vienādojumu, atbildē norādiet sakņu reizinājumu:
Atbilde: sakņu reizinājums ir 8. №4. Atrisiniet vienādojumu:
Apzīmē populācijas vienādojumus (1) un (2) un dizaina ērtībai apsvērt katra no tām risinājumu atsevišķi. Tā kā abos vienādojumos ir vairāk nekā viens modulis, ērtāk ir veikt līdzvērtīgu pāreju uz sistēmu kopām. (1)

(2)


Atbilde:
Vingrinājumi: №36. Atrisiniet vienādojumu, atbildē norādiet sakņu summu: 5 │3x-5│ \u003d 25 x №37. Atrisiniet vienādojumu, ja ir vairākas saknes, atbildē norādiet sakņu summu: │x + 2│ x - 3x - 10 = 1 №38. Atrisiniet vienādojumu: 3 │2x -4│ \u003d 9 │x│ №39. Atrisiniet vienādojumu, atbildē norādiet sakņu skaitu: 2 │ sin x │ = √2 №40 . Atrisiniet vienādojumu, atbildē norādiet sakņu skaitu:

3. sadaļa. Logaritmiskie vienādojumi.

Pirms sekojošo vienādojumu risināšanas nepieciešams pārskatīt logaritmu īpašības un logaritmisko funkciju. Piemēri: №1. Atrisiniet vienādojumu, atbildē norādiet sakņu reizinājumu: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

1. gadījums: ja x ≥ - 1, tad log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – atbilst nosacījumam x ≥ - 1 2 gadījums: ja x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – atbilst nosacījumam x - 1
Atbilde: sakņu reizinājums ir 15.
№2. Atrisiniet vienādojumu, atbildē norādiet sakņu summu: lg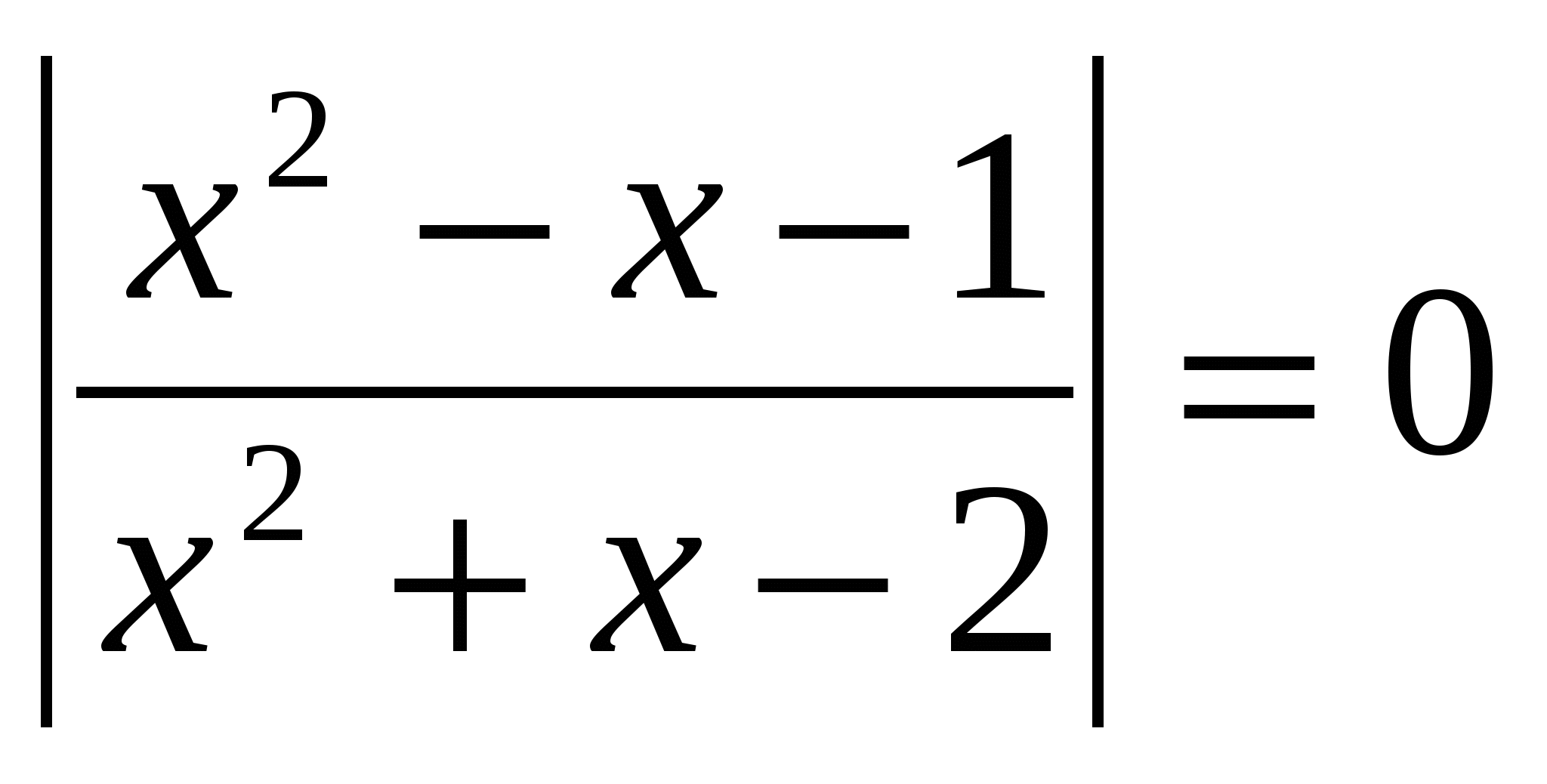
O.D.Z.

Atbilde: sakņu summa ir 0,5.
№3. Atrisiniet vienādojumu: log 5
O.D.Z.

Atbilde: x = 9. №4. Atrisiniet vienādojumu: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Izmantosim formulu pārejai uz citu bāzi. │2 — log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Atradīsim apakšmoduļu izteiksmju nulles: x = 25; x \u003d Šie skaitļi sadala pieļaujamo vērtību laukumu trīs intervālos, tāpēc vienādojums ir līdzvērtīgs trīs sistēmu kopumam.
Atbilde:)