Termenul (modul) în traducere literală din latină înseamnă „măsură”. Acest concept a fost introdus în matematică de omul de știință englez R. Cotes. Și matematicianul german K. Weierstrass a introdus semnul modulului - simbol prin care acest concept este notat la scriere.

In contact cu

Pentru prima dată acest concept este studiat la matematică în cadrul programului clasei a VI-a de liceu. Conform unei definiții, modulul este valoarea absolută a unui număr real. Cu alte cuvinte, pentru a afla modulul unui număr real, trebuie să renunți la semnul acestuia.

Valoarea grafică absolută A notat ca |a|.

Principala trăsătură distinctivă a acestui concept este că este întotdeauna o valoare nenegativă.

Numerele care diferă între ele doar prin semn se numesc numere opuse. Dacă valoarea este pozitivă, atunci opusul său este negativ, iar zero este propriul său opus.

valoare geometrică

Dacă luăm în considerare conceptul de modul din punct de vedere al geometriei, atunci acesta va desemna distanța, care se măsoară în segmente unitare de la origine la punct dat. Această definiție dezvăluie pe deplin sensul geometric al termenului studiat.

Grafic, aceasta poate fi exprimată astfel: |a| = O.A.

Proprietăți de valoare absolută

Mai jos vom lua în considerare toate proprietățile matematice ale acestui concept și modalitățile de scriere sub formă de expresii literale:

Caracteristici ale rezolvării ecuațiilor cu un modul

Dacă vorbim despre rezolvarea ecuațiilor și inegalităților matematice care conțin modul, atunci trebuie să vă amintiți că pentru a le rezolva, va trebui să deschideți acest semn.

De exemplu, dacă semnul valorii absolute conține o expresie matematică, atunci înainte de a deschide modulul, este necesar să se țină cont de definițiile matematice curente.

|A + 5| = A + 5 dacă A este mai mare sau egal cu zero.

5-A dacă A este mai mic decât zero.

În unele cazuri, semnul poate fi extins fără ambiguitate pentru orice valoare a variabilei.

Să luăm în considerare încă un exemplu. Să construim o linie de coordonate, pe care marchem toate valorile numerice, a căror valoare absolută va fi 5.

Mai întâi trebuie să desenați o linie de coordonate, să desemnați originea coordonatelor pe ea și să setați dimensiunea unui singur segment. În plus, linia trebuie să aibă o direcție. Acum pe această linie dreaptă este necesar să se aplice marcaje care vor fi egale cu valoarea unui singur segment.

Astfel, putem observa că pe această linie de coordonate vor exista două puncte de interes pentru noi cu valorile 5 și -5.

MBOU gimnaziu №17 Ivanov

« Ecuații Modulo»
Dezvoltare metodică

Compilat

profesor de matematica

Lebedeva N.V.

20010

Notă explicativă

Capitolul 1 Introducere

Secțiunea 2. Caracteristici principale Secțiunea 3. Interpretarea geometrică a conceptului de modul al unui număr Secțiunea 4. Graficul funcției y = |x| Secțiunea 5 Convenții

capitolul 2

Secțiunea 1. Ecuații de forma |F(х)| = m (protozoare) Secțiunea 2. Ecuații de forma F(|х|) = m Secțiunea 3. Ecuații de forma |F(х)| = G(x) Secțiunea 4. Ecuații de forma |F(х)| = ± F(x) (frumos) Secțiunea 5. Ecuații de forma |F(х)| = |G(x)| Secțiunea 6. Exemple de rezolvare a ecuațiilor nestandard Secțiunea 7. Ecuații de forma |F(х)| + |G(x)| = 0 Secțiunea 8. Ecuații de forma |а 1 x ± в 1 | ± |a 2 x ± în 2 | ± …|a n x ± în n | = m Secțiunea 9. Ecuații care conțin module multiple

Capitolul 3. Exemple de rezolvare a diverselor ecuații cu un modul.

Sectiunea 1. Ecuații trigonometrice Sectiunea 2 ecuații exponențiale Secțiunea 3. Ecuații logaritmice Secțiunea 4. Ecuații iraționale Secțiunea 5. Sarcini de complexitate avansată Răspunsuri la exerciții Bibliografie

Notă explicativă.

Conceptul de valoare absolută (modul) a unui număr real este una dintre caracteristicile sale esențiale. Acest concept este utilizat pe scară largă în diferite ramuri ale științelor fizice, matematice și tehnice. În practica predării unui curs de matematică în liceuîn conformitate cu Programul Ministerului Apărării al Federației Ruse, conceptul de „valoarea absolută a unui număr” apare în mod repetat: în clasa a VI-a, este introdusă definiția modulului, sensul său geometric; în clasa a VIII-a se formează conceptul de eroare absolută, se are în vedere soluția celor mai simple ecuații și inegalități care conțin modulul, se studiază proprietățile rădăcinii pătrate aritmetice; în clasa a XI-a conceptul se regăsește la secțiunea „Rădăcină ngradul”. Experiența de predare arată că elevii întâmpină adesea dificultăți în rezolvarea sarcinilor care necesită cunoașterea acestui material și adesea sar înainte de a începe să le finalizeze. În textele sarcinilor de examen pentru cursul claselor a IX-a și a XI-a sunt incluse și sarcini similare. În plus, cerințele pe care universitățile le impun absolvenților școlii sunt diferite, și anume, de un nivel superior cerințelor din programa școlară. Pentru viața în societatea modernă, este foarte important să se formeze un stil matematic de gândire, care se manifestă în anumite abilități mentale. În procesul de rezolvare a problemelor cu module, este necesară abilitatea de a aplica tehnici precum generalizarea și concretizarea, analiza, clasificarea și sistematizarea, analogia. Rezolvarea unor astfel de sarcini vă permite să verificați cunoștințele principalelor secțiuni ale cursului școlar, nivelul de gândire logică și abilitățile inițiale de cercetare. Această lucrare este dedicată uneia dintre secțiuni - soluția ecuațiilor care conțin modulul. Este format din trei capitole. Primul capitol prezintă conceptele de bază și cele mai importante calcule teoretice. Al doilea capitol propune nouă tipuri de bază de ecuații care conțin modulul, ia în considerare metode de rezolvare a acestora și analizează exemple de diferite niveluri de complexitate. Al treilea capitol oferă ecuații mai complexe și non-standard (trigonometrice, exponențiale, logaritmice și iraționale). Pentru fiecare tip de ecuații există exerciții de rezolvare independentă (se anexează răspunsuri și instrucțiuni). Scopul principal al acestei lucrări este de a oferi asistență metodologică profesorilor în pregătirea lecțiilor și în organizarea cursurilor opționale. Materialul poate fi folosit și ca ghid de studiu pentru elevii de liceu. Sarcinile propuse în lucrare sunt interesante și nu întotdeauna ușor de rezolvat, ceea ce face posibilă conștientizarea motivației de învățare a elevilor, testarea abilităților acestora și îmbunătățirea nivelului de pregătire a absolvenților de școală pentru intrarea în universități. O selecție diferențiată a exercițiilor propuse presupune o trecere de la nivelul reproductiv de asimilare a materialului la cel creativ, precum și posibilitatea de a preda cum să-și aplice cunoștințele în rezolvarea unor probleme nestandardizate.

Capitolul 1 Introducere.

Secțiunea 1. Determinarea valorii absolute .

Definiție : Valoarea absolută (modulul) unui număr real A se numeste numar nenegativ: A sau -A. Desemnare: │ A │ Intrarea sună după cum urmează: „modulul numărului a” sau „valoarea absolută a numărului a”

│ a dacă a > 0

│a│ = │ 0 dacă a = 0 (1)

│ - a, dacă a
Exemple: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Extindeți modulul de expresie:

a) │x - 8│ dacă x > 12 b) │2x + 3│ dacă x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Secțiunea 2. Proprietăți de bază.

Luați în considerare proprietățile de bază ale valorii absolute. Proprietatea #1: Numerele opuse au module egale, adică │а│=│-а│ Să arătăm corectitudinea egalității. Să notăm definiția numărului - A : │- a│= (2) Să comparăm seturile (1) și (2). Evident, definițiile valorilor absolute ale numerelor Ași - A Meci. Prin urmare, │а│=│-а│
Când luăm în considerare următoarele proprietăți, ne limităm la formularea lor, deoarece demonstrația lor este dată în Proprietatea #2: Valoarea absolută a sumei unui număr finit numere reale nu depășește suma valorilor absolute ale termenilor: │a 1 + a 2 +…+ a n Proprietatea #3: Valoarea absolută a diferenței dintre două numere reale nu depășește suma valorilor lor absolute: │а - в│ ≤│а│+│в│ Proprietatea #4: Valoarea absolută a produsului unui număr finit de numere reale este egală cu produsul valorilor absolute ale factorilor: │а · в│=│а│·│в│ Proprietatea #5: Valoarea absolută a câtului numerelor reale este egală cu câtul valorilor lor absolute:

Secțiunea 3. Interpretarea geometrică a conceptului de modul al unui număr.

Fiecare număr real poate fi asociat cu un punct de pe dreapta numerică, care va fi o reprezentare geometrică a acestui număr real. Fiecare punct de pe dreapta numerică corespunde distanței sale de la origine, adică. lungimea segmentului de la origine la punctul dat. Această distanță este întotdeauna considerată o valoare nenegativă. Prin urmare, lungimea segmentului corespunzător va fi interpretarea geometrică a valorii absolute a numărului real dat

Ilustrația geometrică prezentată confirmă în mod clar proprietatea nr. 1, adică. modulele numerelor opuse sunt egale. De aici, validitatea egalității este ușor de înțeles: │x - a│= │a - x│. De asemenea, devine mai evident să se rezolve ecuația │х│= m, unde m ≥ 0, și anume x 1,2 = ± m. Exemple: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; patru

Secțiunea 4. Graficul funcției y \u003d │х│

Domeniul acestei funcții este reprezentat de toate numerele reale.

Secțiunea 5. Simboluri.

În viitor, când se vor lua în considerare exemple de rezolvare a ecuațiilor, se vor folosi următoarele convenții: ( - semnul sistemului [ - semnul setării La rezolvarea unui sistem de ecuații (inegalități) se găsește intersecția soluțiilor ecuațiilor (inegalităților) incluse în sistem. La rezolvarea unei mulțimi de ecuații (inegalități) se găsește o uniune de soluții a ecuațiilor (inegalităților) incluse în mulțime.

capitolul 2

În acest capitol, vom analiza modalități algebrice de a rezolva ecuații care conțin unul sau mai multe module.

Secțiunea 1. Ecuații de forma │F (х) │= m

O ecuație de acest tip se numește cea mai simplă. Are o soluție dacă și numai dacă m ≥ 0. Prin definiția modulului, ecuația inițială este echivalentă cu combinația a două ecuații: │ F(x)│=m
Exemple:
№1. Rezolvați ecuația: │7x - 2│= 9


Raspuns: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 Răspuns: suma rădăcinilor este - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 notează x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – ambele valori satisfac condiția m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Răspuns: numărul de rădăcini ale ecuației 7. Exerciții:
№1. Rezolvați ecuația și indicați suma rădăcinilor: │x - 5│= 3 №2 . Rezolvați ecuația și indicați rădăcina mai mică: │x 2 + x │ \u003d 0 №3 . Rezolvați ecuația și indicați rădăcina mai mare: │x 2 - 5x + 4 │ \u003d 4 №4 .Rezolvați ecuația și indicați întreaga rădăcină: │2x 2 - 7x + 6│ \u003d 1 №5 .Rezolvați ecuația și indicați numărul de rădăcini: │x 4 - 13x 2 + 50 │ = 14

Secțiunea 2. Ecuații de forma F(│х│) = m

Argumentul funcției din partea stângă se află sub semnul modulo, în timp ce partea dreaptă este independentă de variabilă. Să luăm în considerare două moduri de rezolvare a ecuațiilor de acest tip. 1 cale: Prin definiția valorii absolute, ecuația inițială este echivalentă cu totalitatea a două sisteme. În fiecare dintre acestea se impune o condiție expresiei submodulului. F(│х│) =m
Deoarece funcția F(│х│) este pară pe întregul domeniu de definiție, rădăcinile ecuațiilor F(х) = m și F(-х) = m sunt perechi de numere opuse. Așadar, este suficient să rezolvi unul dintre sisteme (luând în considerare exemplele în acest fel, se va da soluția unui sistem). 2 moduri: Aplicarea metodei introducerii unei noi variabile. În acest caz, se introduce denumirea │х│= a, unde a ≥ 0. Aceasta metoda mai puțin voluminos în design.
Exemple: №1 . Rezolvați ecuația: 3x 2 - 4│x│ = - 1 Să folosim introducerea unei noi variabile. Notăm │x│= a, unde a ≥ 0. Obținem ecuația 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Revenim la variabila inițială: │x │ = 1 și │х│= 1/3. Fiecare ecuație are două rădăcini. Raspuns: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rezolvați ecuația: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Să găsim soluția primului sistem de mulțimi: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Rețineți că x 2 face nu satisface condiția x ≥ 0. Prin soluție al doilea sistem va fi numărul opus x 1 . Raspuns: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Rezolvați ecuația: x 4 - │х│= 0 Notăm │х│= a, unde a ≥ 0. Obținem ecuația a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 Revenim la variabila inițială: │х│=0 și │х│= 1 x = 0; ± 1 Raspuns: x 1 = 0; X 2 = 1; X 3 = - 1.
Exerciții: №6. Rezolvați ecuația: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Rezolvați ecuația, în răspuns indicați numărul de rădăcini: 3x 2 - 7│x│ + 2 = 0 №8 . Rezolvați ecuația, în răspuns indicați soluțiile întregi: x 4 + │х│ - 2 = 0

Secțiunea 3. Ecuații de forma │F(х)│ = G(х)

Partea dreaptă a unei ecuații de acest tip depinde de o variabilă și, prin urmare, are o soluție dacă și numai dacă partea dreaptă este o funcție G(x) ≥ 0. Ecuația inițială poate fi rezolvată în două moduri: 1 cale: Standard, bazat pe dezvăluirea modulului pe baza definiției acestuia și constă într-o tranziție echivalentă la combinarea a două sisteme. │ F(x)│ =G(X)

Este rațional să se folosească această metodă în cazul unei expresii complexe pentru funcția G(x) și a unei expresii mai puțin complexe pentru funcția F(x), deoarece se presupune că rezolvă inegalitățile cu funcția F(x). 2 moduri: Constă în trecerea la un sistem echivalent în care se impune o condiție în partea dreaptă. │ F(X)│= G(X)

Această metodă este mai convenabilă de utilizat dacă expresia pentru funcția G(x) este mai puțin complicată decât pentru funcția F(x), deoarece se presupune soluția inegalității G(x) ≥ 0. În plus, în cazul din mai multe module, această metodă este recomandată pentru a utiliza a doua opțiune. Exemple: №1. Rezolvați ecuația: │x + 2│= 6 -2x
(1 sens) Răspuns: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 sensuri) Răspuns: produsul rădăcinilor este 3.
№3. Rezolvați ecuația, în răspuns scrieți suma rădăcinilor:
│x - 6 │ \u003d x 2 - 5x + 9

Răspuns: suma rădăcinilor este 4.
Exerciții: №9. │x + 4│= - 3x №10. Rezolvați ecuația, în răspuns indicați numărul de soluții: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Rezolvați ecuația, în răspuns indicați produsul rădăcinilor: │x + 3 │ \u003d x 2 + x - 6

Secțiunea 4. Ecuații de forma │F(x)│= F(x) și │F(x)│= - F(x)

Ecuațiile de acest tip sunt uneori numite „frumoase”. Deoarece partea dreaptă a ecuațiilor depinde de variabilă, există soluții dacă și numai dacă partea dreaptă este nenegativă. Prin urmare, ecuațiile inițiale sunt echivalente cu inegalitățile:
│F(x)│= F(x) F(x) ≥ 0 și │F(x)│= - F(x) F(x) Exemple: №1 . Rezolvați ecuația, în răspuns indicați rădăcina întreagă mai mică: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Răspuns: x = 1№2. Rezolvați ecuația, în răspuns indicați lungimea decalajului: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Răspuns: lungimea decalajului este de 6.№3 . Rezolvați ecuația, în răspuns indicați numărul de soluții întregi: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Răspuns: 4 soluții întregi.№4 . Rezolvați ecuația, în răspuns indicați cea mai mare rădăcină:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Răspuns: x = 3.

Exerciții: №12. Rezolvați ecuația, în răspuns indicați întreaga rădăcină: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Rezolvați ecuația, în răspuns indicați numărul de soluții întregi: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Rezolvați ecuația, în răspuns indicați un număr întreg care nu este rădăcina ecuației:

Secțiunea 5. Ecuații de forma │F(x)│= │G(x)│

Deoarece ambele părți ale ecuației sunt nenegative, soluția implică luarea în considerare a două cazuri: expresiile submodulelor sunt egale sau opuse ca semn. Prin urmare, ecuația inițială este echivalentă cu combinația a două ecuații: │ F(X)│= │ G(X)│
Exemple: №1. Rezolvați ecuația, în răspuns indicați întreaga rădăcină: │x + 3│ \u003d │2x - 1│
Răspuns: rădăcină întreagă x = 4.№2. Rezolvați ecuația: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Răspuns: x = 2.№3 . Rezolvați ecuația, în răspuns indicați produsul rădăcinilor:




Rădăcinile ecuației 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Răspuns: produsul rădăcinilor este 0,25. Exerciții: №15 . Rezolvați ecuația, în răspuns indicați întreaga soluție: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Rezolvați ecuația, în răspuns indicați rădăcina mai mică: │5x - 3│=│7 - x│ №17 . Rezolvați ecuația, în răspuns scrieți suma rădăcinilor:

Secțiunea 6. Exemple de rezolvare a ecuațiilor nestandard

În această secțiune, luăm în considerare exemple de ecuații non-standard, în soluția cărora valoarea absolută a expresiei este relevată prin definiție. Exemple:

№1. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: x │x│- 5x - 6 \u003d 0
Răspuns: suma rădăcinilor este 1 №2. . Rezolvați ecuația, în răspuns indicați rădăcina mai mică: x 2 - 4x
- 5 = 0
Răspuns: rădăcină mai mică x = - 5. №3. Rezolvați ecuația:

Răspuns: x = -1. Exerciții: №18. Rezolvați ecuația și scrieți suma rădăcinilor: x │3x + 5│= 3x 2 + 4x + 3
№19. Rezolvați ecuația: x 2 - 3x \u003d

№20. Rezolvați ecuația:

Secțiunea 7. Ecuații de forma │F(x)│+│G(x)│=0

Este ușor de observat că în partea stângă a unei ecuații de acest tip, suma cantităților nenegative. Prin urmare, ecuația originală are o soluție dacă și numai dacă ambii termeni sunt egali simultan cu zero. Ecuația este echivalentă cu sistemul de ecuații: │ F(X)│+│ G(X)│=0
Exemple: №1 . Rezolvați ecuația:
Răspuns: x = 2. №2. Rezolvați ecuația: Răspuns: x = 1. Exerciții: №21. Rezolvați ecuația: №22 . Rezolvați ecuația, în răspuns scrieți suma rădăcinilor: №23 . Rezolvați ecuația, în răspuns indicați numărul de soluții:

Secțiunea 8. Ecuații de formă

Pentru rezolvarea ecuațiilor de acest tip se folosește metoda intervalelor. Dacă se rezolvă prin extinderea secvențială a modulelor, atunci obținem n seturi de sisteme, ceea ce este foarte greoi și incomod. Luați în considerare algoritmul metodei intervalului: 1). Găsiți valori variabile X, pentru care fiecare modul este egal cu zero (zerouri de expresii ale submodulului):
2). Valorile găsite sunt marcate pe o linie numerică, care este împărțită în intervale (numărul de intervale, respectiv, este egal cu n+1 ) 3). Stabiliți cu ce semn se dezvăluie fiecare modul la fiecare dintre intervalele obținute (când faceți o soluție, puteți folosi o linie numerică, marcând semnele pe ea) 4). Ecuația inițială este echivalentă cu mulțimea n+1 sisteme, în fiecare dintre care este indicată apartenența variabilei X unul dintre intervale. Exemple: №1 . Rezolvați ecuația, în răspuns indicați cea mai mare rădăcină:
unu). Să găsim zerourile expresiilor submodulelor: x = 2; x = -3 2). Marcam valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- fără soluții Ecuația are două rădăcini. Răspuns: cea mai mare rădăcină este x = 2. №2. Rezolvați ecuația, scrieți întreaga rădăcină în răspuns:
unu). Să găsim zerourile expresiilor submodulelor: x = 1,5; x = - 1 2). Marcam valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Ultimul sistem nu are soluții, prin urmare, ecuația are două rădăcini. Când rezolvați ecuația, ar trebui să acordați atenție semnului „-” din fața celui de-al doilea modul. Răspuns: rădăcină întreagă x = 7. №3. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: 1). Să găsim zerourile expresiilor submodulelor: x = 5; x = 1; x = - 2 2). Marcăm valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Ecuația are două rădăcini x = 0 și 2. Răspuns: suma rădăcinilor este 2. №4 . Rezolvați ecuația: 1). Să găsim zerourile expresiilor submodulelor: x = 1; x = 2; x = 3. 2). Să determinăm semnul cu care fiecare modul este extins pe intervalele obținute. 3).
Să combinăm soluțiile primei trei sisteme. Răspuns: ; x = 5.
Exerciții: №24. Rezolvați ecuația:
№25. Rezolvați ecuația, în răspuns scrieți suma rădăcinilor: №26. Rezolvați ecuația, în răspuns indicați rădăcina mai mică: №27. Rezolvați ecuația, dați rădăcina mai mare în răspunsul dvs.:

Secțiunea 9. Ecuații care conțin module multiple

Ecuațiile care conțin mai multe module presupun prezența valorilor absolute în expresiile submodulelor. Principiul de bază al rezolvării ecuațiilor de acest tip este dezvăluirea secvențială a modulelor, începând cu cele „externe”. În cursul soluției se folosesc tehnicile discutate în secțiunile nr. 1, nr. 3.

Exemple: №1. Rezolvați ecuația:
Răspuns: x = 1; - unsprezece. №2. Rezolvați ecuația:
Răspuns: x = 0; patru; - patru. №3. Rezolvați ecuația, în răspuns indicați produsul rădăcinilor:
Răspuns: produsul rădăcinilor este 8. №4. Rezolvați ecuația:
Notați ecuațiile populației (1) și (2) și luați în considerare soluția fiecăruia dintre ele separat pentru comoditatea designului. Deoarece ambele ecuații conțin mai mult de un modul, este mai convenabil să se efectueze o tranziție echivalentă la seturi de sisteme. (1)

(2)


Răspuns:
Exerciții: №36. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: 5 │3x-5│ \u003d 25 x №37. Rezolvați ecuația, dacă există mai multe rădăcini, în răspuns indicați suma rădăcinilor: │x + 2│ x - 3x - 10 = 1 №38. Rezolvați ecuația: 3 │2x -4│ \u003d 9 │x│ №39. Rezolvați ecuația, în răspuns indicați numărul de rădăcini pentru: 2 │ sin x │ = √2 №40 . Rezolvați ecuația, în răspuns indicați numărul de rădăcini:

Secțiunea 3. Ecuații logaritmice.

Înainte de a rezolva următoarele ecuații, este necesar să trecem în revistă proprietățile logaritmilor și ale funcției logaritmice. Exemple: №1. Rezolvați ecuația, în răspuns indicați produsul rădăcinilor: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

Cazul 1: dacă x ≥ - 1, atunci log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisface condiția x ≥ - 1 2 caz: dacă x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisface condiția x - 1
Răspuns: produsul rădăcinilor este 15.
№2. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: lg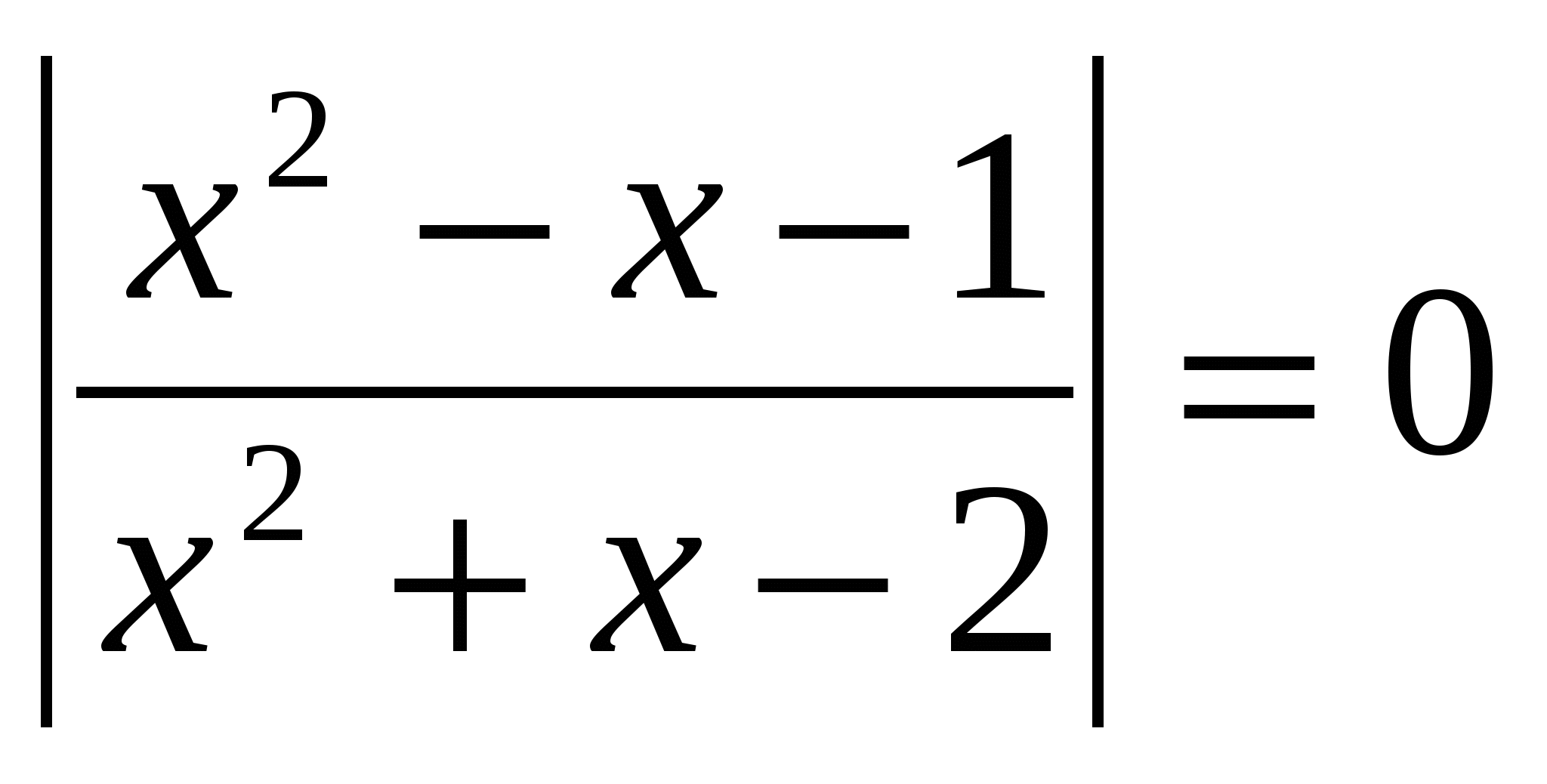
O.D.Z.

Răspuns: suma rădăcinilor este 0,5.
№3. Rezolvați ecuația: log 5
O.D.Z.

Răspuns: x = 9. №4. Rezolvați ecuația: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Să folosim formula pentru a trece la o altă bază. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Să ​​aflăm zerourile expresiilor submodulelor: x = 25; x \u003d Aceste numere împart aria valorilor permise în trei intervale, astfel încât ecuația este echivalentă cu totalitatea a trei sisteme.
Răspuns: )