Cili është logaritmi i njërit? Shndërrimi i shprehjeve duke përdorur vetitë e logaritmeve: shembuj, zgjidhje

Siç e dini, kur shumëzohen shprehjet me fuqi, eksponentët e tyre gjithmonë mblidhen (a b *a c = a b+c). Ky ligj matematik u nxor nga Arkimedi, dhe më vonë, në shekullin e 8-të, matematikani Virasen krijoi një tabelë të eksponentëve të numrave të plotë. Ishin ata që shërbyen për zbulimin e mëtejshëm të logaritmeve. Shembuj të përdorimit të këtij funksioni mund të gjenden pothuajse kudo ku duhet të thjeshtoni shumëzimin e rëndë me mbledhje të thjeshtë. Nëse kaloni 10 minuta duke lexuar këtë artikull, ne do t'ju shpjegojmë se çfarë janë logaritmet dhe si të punoni me to. Në një gjuhë të thjeshtë dhe të arritshme.

Përkufizimi në matematikë

Një logaritëm është një shprehje e formës së mëposhtme: log a b=c, d.m.th., logaritmi i çdo numri jonegativ (d.m.th., çdo pozitiv) "b" në bazën e tij "a" konsiderohet të jetë fuqia "c. ” në të cilën baza “a” duhet të ngrihet për të marrë në fund vlerën “b”. Le të analizojmë logaritmin duke përdorur shembuj, le të themi se ka një shprehje log 2 8. Si të gjejmë përgjigjen? Është shumë e thjeshtë, ju duhet të gjeni një fuqi të tillë që nga 2 në fuqinë e kërkuar të merrni 8. Pasi të keni bërë disa llogaritje në kokën tuaj, marrim numrin 3! Dhe kjo është e vërtetë, sepse 2 në fuqinë e 3 jep përgjigjen si 8.

Llojet e logaritmeve

Për shumë studentë kjo temë duket e ndërlikuar dhe e pakuptueshme, por në fakt logaritmet nuk janë aq të frikshme, gjëja kryesore është të kuptoni kuptimin e tyre të përgjithshëm dhe të mbani mend vetitë e tyre dhe disa rregulla. Ekzistojnë tre lloje të veçanta të shprehjeve logaritmike:

1. Logaritmi natyror ln a, ku baza është numri i Euler-it (e = 2.7).
2. Dhjetor a, ku baza është 10.
3. Logaritmi i çdo numri b në bazën a>1.

Secila prej tyre zgjidhet në një mënyrë standarde, duke përfshirë thjeshtimin, reduktimin dhe reduktimin pasues në një logaritëm të vetëm duke përdorur teorema logaritmike. Për të marrë vlerat e sakta të logaritmeve, duhet të mbani mend vetitë e tyre dhe sekuencën e veprimeve gjatë zgjidhjes së tyre.

Rregulla dhe disa kufizime

Në matematikë ka disa rregulla-kufizime që pranohen si aksiomë, pra nuk janë objekt diskutimi dhe janë të vërteta. Për shembull, është e pamundur të ndash numrat me zero, dhe është gjithashtu e pamundur të nxjerrësh rrënjën çift të numrave negativë. Logaritmet gjithashtu kanë rregullat e tyre, duke ndjekur të cilat lehtë mund të mësoni të punoni edhe me shprehje logaritmike të gjata dhe të mëdha:

• Baza "a" duhet të jetë gjithmonë më e madhe se zero dhe jo e barabartë me 1, përndryshe shprehja do të humbasë kuptimin e saj, sepse "1" dhe "0" në çdo shkallë janë gjithmonë të barabarta me vlerat e tyre;
• nëse a > 0, atëherë a b >0, rezulton se edhe “c” duhet të jetë më e madhe se zero.

Si të zgjidhni logaritmet?

Për shembull, jepet detyra për të gjetur përgjigjen e ekuacionit 10 x = 100. Kjo është shumë e lehtë, ju duhet të zgjidhni një fuqi duke ngritur numrin dhjetë në të cilin marrim 100. Kjo, natyrisht, është 10 2 = 100.

Tani le ta paraqesim këtë shprehje në formë logaritmike. Marrim log 10 100 = 2. Kur zgjidhim logaritme, të gjitha veprimet praktikisht konvergojnë për të gjetur fuqinë në të cilën është e nevojshme të futet baza e logaritmit për të marrë një numër të caktuar.

Për të përcaktuar me saktësi vlerën e një shkalle të panjohur, duhet të mësoni se si të punoni me një tabelë gradash. Duket kështu:

Siç mund ta shihni, disa eksponentë mund të merren me mend në mënyrë intuitive nëse keni një mendje teknike dhe njohuri për tabelën e shumëzimit. Sidoqoftë, për vlera më të mëdha do t'ju duhet një tavolinë energjie. Mund të përdoret edhe nga ata që nuk dinë fare për tema komplekse matematikore. Kolona e majtë përmban numra (baza a), rreshti i sipërm i numrave është vlera e fuqisë c në të cilën është ngritur numri a. Në kryqëzim, qelizat përmbajnë vlerat e numrave që janë përgjigja (a c =b). Le të marrim, për shembull, qelizën e parë me numrin 10 dhe ta katrorojmë atë, marrim vlerën 100, e cila tregohet në kryqëzimin e dy qelizave tona. Gjithçka është aq e thjeshtë dhe e lehtë sa që edhe humanisti më i vërtetë do ta kuptojë!

Ekuacionet dhe pabarazitë

Rezulton se në kushte të caktuara eksponenti është logaritmi. Prandaj, çdo shprehje numerike matematikore mund të shkruhet si barazi logaritmike. Për shembull, 3 4 = 81 mund të shkruhet si logaritmi bazë 3 i 81 i barabartë me katër (log 3 81 = 4). Për fuqitë negative rregullat janë të njëjta: 2 -5 = 1/32 e shkruajmë si logaritëm, marrim log 2 (1/32) = -5. Një nga seksionet më tërheqëse të matematikës është tema e "logaritmeve". Ne do të shikojmë shembujt dhe zgjidhjet e ekuacioneve më poshtë, menjëherë pasi të studiojmë vetitë e tyre. Tani le të shohim se si duken pabarazitë dhe si t'i dallojmë ato nga ekuacionet.

Është dhënë shprehja e mëposhtme: log 2 (x-1) > 3 - është një pabarazi logaritmike, pasi vlera e panjohur "x" është nën shenjën logaritmike. Dhe gjithashtu në shprehjen krahasohen dy madhësi: logaritmi i numrit të dëshiruar me bazën dy është më i madh se numri tre.

Dallimi më i rëndësishëm midis ekuacioneve logaritmike dhe pabarazive është se ekuacionet me logaritme (për shembull, logaritmi 2 x = √9) nënkuptojnë një ose më shumë vlera numerike specifike në përgjigje, ndërsa kur zgjidhet një pabarazi, të dy diapazoni i pranueshëm vlerat dhe pikat përcaktohen duke thyer këtë funksion. Si pasojë, përgjigja nuk është një grup i thjeshtë numrash individualë, si në përgjigjen e një ekuacioni, por një seri e vazhdueshme ose grup numrash.

Teorema themelore rreth logaritmeve

Kur zgjidhni detyra primitive për gjetjen e vlerave të logaritmit, vetitë e tij mund të mos dihen. Megjithatë, kur bëhet fjalë për ekuacionet logaritmike ose pabarazitë, para së gjithash, është e nevojshme të kuptohen qartë dhe të zbatohen në praktikë të gjitha vetitë themelore të logaritmeve. Ne do t'i shikojmë shembujt e ekuacioneve më vonë, le të shohim më në detaje secilën veçori.

1. Identiteti kryesor duket si ky: a logaB =B. Zbatohet vetëm kur a është më e madhe se 0, jo e barabartë me një, dhe B është më e madhe se zero.
2. Logaritmi i produktit mund të paraqitet në formulën e mëposhtme: log d (s 1 * s 2) = log d s 1 + log d s 2. Në këtë rast, kushti i detyrueshëm është: d, s 1 dhe s 2 > 0; a≠1. Ju mund të jepni një provë për këtë formulë logaritmike, me shembuj dhe zgjidhje. Le të log a s 1 = f 1 dhe log a s 2 = f 2, pastaj a f1 = s 1, a f2 = s 2. Marrim se s 1 * s 2 = a f1 *a f2 = a f1+f2 (vetitë e gradë ), dhe më pas sipas përkufizimit: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, që është ajo që duhej vërtetuar.
3. Logaritmi i herësit duket kështu: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Teorema në formën e një formule merr formën e mëposhtme: log a q b n = n/q log a b.

Kjo formulë quhet "vetia e shkallës së logaritmit". Ajo i ngjan vetive të shkallëve të zakonshme dhe nuk është për t'u habitur, sepse e gjithë matematika bazohet në postulate natyrore. Le të shohim provën.

Le të log a b = t, rezulton një t =b. Nëse i ngremë të dyja pjesët në fuqinë m: a tn = b n ;

por meqenëse a tn = (a q) nt/q = b n, prandaj log a q b n = (n*t)/t, atëherë log a q b n = n/q log a b. Teorema është vërtetuar.

Shembuj të problemeve dhe pabarazive

Llojet më të zakonshme të problemeve në logaritme janë shembuj të ekuacioneve dhe pabarazive. Ato gjenden pothuajse në të gjitha librat me probleme, si dhe janë pjesë e detyrueshme e provimeve të matematikës. Për të hyrë në një universitet ose për të kaluar provimet pranuese në matematikë, duhet të dini se si t'i zgjidhni saktë detyra të tilla.

Fatkeqësisht, nuk ka asnjë plan ose skemë të vetme për zgjidhjen dhe përcaktimin e vlerës së panjohur të logaritmit, por disa rregulla mund të zbatohen për çdo pabarazi matematikore ose ekuacion logaritmik. Para së gjithash, duhet të zbuloni nëse shprehja mund të thjeshtohet ose reduktohet në një formë të përgjithshme. Ju mund të thjeshtoni shprehjet e gjata logaritmike nëse përdorni saktë vetitë e tyre. Le t'i njohim shpejt.

Kur zgjidhim ekuacione logaritmike, duhet të përcaktojmë se çfarë lloj logaritmi kemi: një shprehje shembull mund të përmbajë një logaritëm natyror ose një dhjetor.

Këtu janë shembuj ln100, ln1026. Zgjidhja e tyre zbret në faktin se ata duhet të përcaktojnë fuqinë në të cilën baza 10 do të jetë e barabartë me 100 dhe 1026, përkatësisht. Për të zgjidhur logaritmet natyrore, duhet të aplikoni identitete logaritmike ose vetitë e tyre. Le të shohim shembuj të zgjidhjes së problemeve logaritmike të llojeve të ndryshme.

Si të përdorni formulat e logaritmit: me shembuj dhe zgjidhje

Pra, le të shohim shembuj të përdorimit të teoremave bazë rreth logaritmeve.

1. Vetia e logaritmit të një produkti mund të përdoret në detyra ku është e nevojshme të zbërthehet një vlerë e madhe e numrit b në faktorë më të thjeshtë. Për shembull, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Përgjigja është 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - siç mund ta shihni, duke përdorur vetinë e katërt të fuqisë së logaritmit, arritëm të zgjidhim një shprehje në dukje komplekse dhe të pazgjidhshme. Thjesht duhet të faktorizoni bazën dhe më pas të hiqni vlerat e eksponentit nga shenja e logaritmit.

Detyra nga Provimi i Unifikuar i Shtetit

Logaritmet gjenden shpesh në provimet pranuese, veçanërisht shumë probleme logaritmike në Provimin e Unifikuar të Shtetit (provim shtetëror për të gjithë maturantët). Në mënyrë tipike, këto detyra janë të pranishme jo vetëm në pjesën A (pjesa më e lehtë testuese e provimit), por edhe në pjesën C (detyrat më komplekse dhe më voluminoze). Provimi kërkon njohuri të sakta dhe të përsosura të temës “Logaritmet natyrore”.

Shembujt dhe zgjidhjet e problemeve janë marrë nga versionet zyrtare të Provimit të Unifikuar të Shtetit. Le të shohim se si zgjidhen detyra të tilla.

Jepet log 2 (2x-1) = 4. Zgjidhje:
le ta rishkruajmë shprehjen, duke e thjeshtuar pak log 2 (2x-1) = 2 2, me përcaktimin e logaritmit marrim se 2x-1 = 2 4, pra 2x = 17; x = 8,5.

• Është mirë që të reduktohen të gjitha logaritmet në të njëjtën bazë në mënyrë që zgjidhja të mos jetë e rëndë dhe konfuze.
• Të gjitha shprehjet nën shenjën e logaritmit tregohen si pozitive, prandaj, kur eksponenti i një shprehjeje që është nën shenjën e logaritmit dhe si bazë e saj nxirret si shumëzues, shprehja e mbetur nën logaritëm duhet të jetë pozitive.

Sot do të flasim për formulat e logaritmit dhe japin tregues shembuj zgjidhjesh.

Ata vetë nënkuptojnë modele zgjidhjesh sipas vetive themelore të logaritmeve. Përpara se të aplikoni formula logaritmike për zgjidhje, le t'ju kujtojmë të gjitha vetitë:

Tani, bazuar në këto formula (veti), do të tregojmë shembuj të zgjidhjes së logaritmeve.

Shembuj të zgjidhjes së logaritmeve bazuar në formula.

Logaritmi një numër pozitiv b për bazën a (i shënuar me log a b) është një eksponent tek i cili duhet të rritet a për të marrë b, me b > 0, a > 0 dhe 1.

Sipas përkufizimit, log a b = x, që është ekuivalente me a x = b, pra log a a x = x.

Logaritmet, shembuj:

log 2 8 = 3, sepse 2 3 = 8

log 7 49 = 2, sepse 7 2 = 49

log 5 1/5 = -1, sepse 5 -1 = 1/5

Logaritmi dhjetor- ky është një logaritëm i zakonshëm, baza e të cilit është 10. Shënohet si lg.

log 10 100 = 2, sepse 10 2 = 100

Logaritmi natyror- gjithashtu një logaritëm i zakonshëm, një logaritëm, por me bazën e (e = 2,71828... - një numër irracional). Shënuar si ln.

Këshillohet që formulat ose vetitë e logaritmeve të mësohen përmendësh, sepse ato do të na duhen më vonë gjatë zgjidhjes së logaritmeve, ekuacioneve logaritmike dhe pabarazive. Le të shqyrtojmë secilën formulë përsëri me shembuj.

• Identiteti bazë logaritmik
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Logaritmi i produktit është i barabartë me shumën e logaritmeve
  log a (bc) = log a b + log a c

  log 3 8.1 + log 3 10 = log 3 (8.1*10) = log 3 81 = 4

• Logaritmi i herësit është i barabartë me diferencën e logaritmeve
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Vetitë e fuqisë së një numri logaritmik dhe bazës së logaritmit

  Eksponenti i numrit logaritmik log a b m = mlog a b

  Eksponenti i bazës së logaritmit log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  nëse m = n, marrim log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Kalimi në një themel të ri
  log a b = log c b/log c a,

  nëse c = b, marrim log b b = 1

  atëherë log a b = 1/log b a

  log 0.8 3*log 3 1.25 = log 0.8 3*log 0.8 1.25/log 0.8 3 = log 0.8 1.25 = log 4/5 5/4 = -1

Siç mund ta shihni, formulat për logaritmet nuk janë aq të komplikuara sa duken. Tani, pasi kemi parë shembuj të zgjidhjes së logaritmeve, mund të kalojmë te ekuacionet logaritmike. Ne do të shikojmë shembuj të zgjidhjes së ekuacioneve logaritmike në mënyrë më të detajuar në artikullin: "". Mos humbasë!

Nëse keni ende pyetje në lidhje me zgjidhjen, shkruajini ato në komentet e artikullit.

Shënim: ne vendosëm të merrnim një klasë tjetër arsimimi dhe të studionim jashtë vendit si opsion.

Logaritmi i një numri N bazuar në A i quajtur eksponent X , në të cilën ju duhet të ndërtoni A për të marrë numrin N

Me kusht që
,
,

Nga përkufizimi i logaritmit del se
, d.m.th.
- kjo barazi është identiteti bazë logaritmik.

Logaritmet me bazën 10 quhen logaritme dhjetore. Në vend të
shkruaj
.

Logaritmet në bazë e quhen natyrore dhe caktohen
.

Vetitë themelore të logaritmeve.

Logaritmi i një është i barabartë me zero për çdo bazë.

Logaritmi i produktit është i barabartë me shumën e logaritmeve të faktorëve.

3) Logaritmi i herësit është i barabartë me diferencën e logaritmeve

Faktori
quhet moduli i kalimit nga logaritmet në bazë a te logaritmet në bazë b .

Duke përdorur vetitë 2-5, shpesh është e mundur të reduktohet logaritmi i një shprehjeje komplekse në rezultatin e veprimeve të thjeshta aritmetike në logaritme.

Për shembull,

Shndërrime të tilla të një logaritmi quhen logaritme. Shndërrimet e kundërta me logaritmet quhen fuqizim.

Kapitulli 2. Elementet e matematikës së lartë.

1. Kufijtë

Kufiri i funksionit
është një numër i fundëm A nëse, si xx 0 për çdo të paracaktuar
, ekziston një numër i tillë
që sapo
, Kjo
.

Një funksion që ka një kufi ndryshon prej tij me një sasi infinite të vogël:
, ku- b.m.v., d.m.th.
.

Shembull. Merrni parasysh funksionin
.

Kur përpiqet
, funksion y priret në zero:

1.1. Teorema themelore rreth kufijve.

Kufiri i një vlere konstante është i barabartë me këtë vlerë konstante

.

Kufiri i shumës (diferencës) i një numri të fundëm funksionesh është i barabartë me shumën (diferencën) e kufijve të këtyre funksioneve.

Kufiri i prodhimit të një numri të kufizuar funksionesh është i barabartë me produktin e kufijve të këtyre funksioneve.

Kufiri i herësit të dy funksioneve është i barabartë me herësin e kufijve të këtyre funksioneve nëse kufiri i emëruesit nuk është zero.

Kufij të mrekullueshëm

,
, Ku

1.2. Shembuj të llogaritjes së kufirit

Sidoqoftë, jo të gjitha kufijtë llogariten kaq lehtë. Më shpesh, llogaritja e kufirit zbret në zbulimin e një pasigurie të llojit: ose .

.

2. Derivat i një funksioni

Le të kemi një funksion
, e vazhdueshme në segment
.

Argumenti ka pasur një rritje
. Pastaj funksioni do të marrë një rritje
.

Vlera e argumentit korrespondon me vlerën e funksionit
.

Vlera e argumentit
korrespondon me vlerën e funksionit.

Prandaj, .

Le të gjejmë kufirin e këtij raporti në
. Nëse ky kufi ekziston, atëherë ai quhet derivat i funksionit të dhënë.

Përkufizimi 3 Derivat i një funksioni të dhënë
me argument quhet kufiri i raportit të rritjes së një funksioni me rritjen e argumentit, kur rritja e argumentit tenton në mënyrë arbitrare në zero.

Derivat i një funksioni
mund të caktohet si më poshtë:

; ; ; .

Përkufizimi 4Veprimi i gjetjes së derivatit të një funksioni quhet diferencimi.

2.1. Kuptimi mekanik i derivatit.

Le të shqyrtojmë lëvizjen drejtvizore të një trupi të ngurtë ose pikë materiale.

Lëreni në një moment në kohë pikë lëvizëse
ishte në distancë nga pozicioni i fillimit
.

Pas një periudhe kohe
ajo lëvizi një distancë
. Qëndrimi =- shpejtësia mesatare e një pike materiale
. Le të gjejmë kufirin e këtij raporti, duke marrë parasysh atë
.

Për rrjedhojë, përcaktimi i shpejtësisë së menjëhershme të lëvizjes së një pike materiale reduktohet në gjetjen e derivatit të shtegut në lidhje me kohën.

2.2. Vlera gjeometrike e derivatit

Le të kemi një funksion të përcaktuar grafikisht
.

Oriz. 1. Kuptimi gjeometrik i derivatit

Nëse
, pastaj tregoni
, do të lëvizë përgjatë kurbës, duke iu afruar pikës
.

Prandaj
, d.m.th. vlera e derivatit për një vlerë të caktuar të argumentit numerikisht e barabartë me tangjenten e këndit të formuar nga tangjentja në një pikë të caktuar me drejtimin pozitiv të boshtit
.

2.3. Tabela e formulave bazë të diferencimit.

Funksioni i fuqisë

Funksioni eksponencial

Funksioni logaritmik

Funksioni trigonometrik

Funksioni trigonometrik i anasjelltë

2.4. Rregullat e diferencimit.

Derivat i

Derivat i shumës (diferencës) së funksioneve

Derivat i prodhimit të dy funksioneve

Derivat i herësit të dy funksioneve

2.5. Derivat i një funksioni kompleks.

Le të jepet funksioni
e tillë që mund të paraqitet në formë

Dhe
, ku ndryshorja është një argument i ndërmjetëm, pra

Derivati ​​i një funksioni kompleks është i barabartë me produktin e derivatit të funksionit të dhënë në lidhje me argumentin e ndërmjetëm dhe derivatin e argumentit të ndërmjetëm në lidhje me x.

Shembulli 1.

Shembulli 2.

3. Funksioni diferencial.

Le të ketë
, i diferencueshëm në disa intervale
le të shkojë në ky funksion ka një derivat

,

atëherë mund të shkruajmë

(1),

Ku - një sasi pafundësisht e vogël,

qe kur

Duke shumëzuar të gjitha kushtet e barazisë (1) me
ne kemi:

Ku
- b.m.v. rendit më të lartë.

Madhësia
quhet diferencial i funksionit
dhe është caktuar

.

3.1. Vlera gjeometrike e diferencialit.

Le të jepet funksioni
.

Fig.2. Kuptimi gjeometrik i diferencialit.

.

Natyrisht, diferenciali i funksionit
është e barabartë me shtimin e ordinatës së tangjentes në një pikë të caktuar.

3.2. Derivatet dhe diferencialet e rendeve te ndryshme.

Nëse atje
, Pastaj
quhet derivati ​​i parë.

Derivati ​​i derivatit të parë quhet derivat i rendit të dytë dhe shkruhet
.

Derivat i rendit të n-të të funksionit
quhet derivat i rendit (n-1) dhe shkruhet:

.

Diferenciali i diferencialit të një funksioni quhet diferencial i dytë ose diferencial i rendit të dytë.

.

.

3.3 Zgjidhja e problemeve biologjike duke përdorur diferencimin.

Detyra 1. Studimet kanë treguar se rritja e një kolonie mikroorganizmash i bindet ligjit
, Ku N - numri i mikroorganizmave (në mijëra), t – koha (ditët).

b) A do të rritet apo ulet popullsia e kolonisë gjatë kësaj periudhe?

Përgjigju. Madhësia e kolonisë do të rritet.

Detyra 2. Uji në liqen testohet periodikisht për të monitoruar përmbajtjen e baktereve patogjene. përmes t ditë pas testimit, përqendrimi i baktereve përcaktohet nga raporti

.

Kur liqeni do të ketë një përqendrim minimal të baktereve dhe a do të jetë e mundur të notosh në të?

Zgjidhje: Një funksion arrin max ose min kur derivati ​​i tij është zero.

,

Le të përcaktojmë se maksimumi ose min do të jetë në 6 ditë. Për ta bërë këtë, le të marrim derivatin e dytë.

Përgjigje: Pas 6 ditësh do të ketë një përqendrim minimal të baktereve.

Gama e vlerave të pranueshme (APV) të logaritmit

Tani le të flasim për kufizimet (ODZ - diapazoni i vlerave të lejuara të variablave).

Kujtojmë se, për shembull, rrënja katrore nuk mund të merret nga numrat negativë; ose nëse kemi një thyesë, atëherë emëruesi nuk mund të jetë i barabartë me zero. Logaritmet kanë kufizime të ngjashme:

Kjo do të thotë, edhe argumenti edhe baza duhet të jenë më të mëdha se zero, por baza nuk mund të jetë ende e barabartë.

Pse eshte ajo?

Le të fillojmë me një gjë të thjeshtë: le të themi këtë. Atëherë, për shembull, numri nuk ekziston, pasi pavarësisht se në çfarë fuqie ngremë, gjithmonë rezulton. Për më tepër, ajo nuk ekziston për askënd. Por në të njëjtën kohë mund të jetë e barabartë me çdo gjë (për të njëjtën arsye - e barabartë me çdo shkallë). Prandaj, objekti nuk paraqet interes dhe thjesht u hodh nga matematika.

Ne kemi një problem të ngjashëm në rastin: për çdo fuqi pozitive është, por nuk mund të ngrihet fare në një fuqi negative, pasi kjo do të rezultojë në pjesëtim me zero (më lejoni t'ju kujtoj se).

Kur përballemi me problemin e ngritjes në një fuqi thyesore (që paraqitet si rrënjë: . Për shembull, (d.m.th.), por ajo nuk ekziston.

Prandaj, është më e lehtë të flakësh arsyet negative sesa të ngacmosh me to.

Epo, meqenëse baza jonë a mund të jetë vetëm pozitive, atëherë pavarësisht se në çfarë fuqie e ngremë atë, ne gjithmonë do të marrim një numër rreptësisht pozitiv. Pra, argumenti duhet të jetë pozitiv. Për shembull, ai nuk ekziston, pasi nuk do të jetë një numër negativ në asnjë shkallë (apo edhe zero, prandaj edhe ai nuk ekziston).

Në problemet me logaritmet, gjëja e parë që duhet të bëni është të shkruani ODZ. Më lejoni t'ju jap një shembull:

Le të zgjidhim ekuacionin.

Le të kujtojmë përkufizimin: një logaritëm është fuqia në të cilën baza duhet të ngrihet për të marrë një argument. Dhe sipas kushtit kjo shkallë është e barabartë me: .

Marrim ekuacionin e zakonshëm kuadratik: . Le ta zgjidhim duke përdorur teoremën e Vietës: shuma e rrënjëve është e barabartë dhe prodhimi. Lehtë për t'u marrë, këto janë numra dhe.

Por nëse menjëherë i merrni dhe i shkruani të dy këta numra në përgjigje, mund të merrni 0 pikë për problemin. Pse? Le të mendojmë se çfarë ndodh nëse i zëvendësojmë këto rrënjë në ekuacionin fillestar?

Kjo është qartësisht e pasaktë, pasi baza nuk mund të jetë negative, domethënë rrënja është "palë e tretë".

Për të shmangur grackat e tilla të pakëndshme, duhet të shkruani ODZ edhe para se të filloni të zgjidhni ekuacionin:

Pastaj, pasi kemi marrë rrënjët dhe, ne menjëherë e hedhim rrënjën dhe shkruajmë përgjigjen e saktë.

Shembulli 1(përpiqu ta zgjidhësh vetë) :

Gjeni rrënjën e ekuacionit. Nëse ka disa rrënjë, tregoni më të voglin prej tyre në përgjigjen tuaj.

Zgjidhja:

Para së gjithash, le të shkruajmë ODZ:

Tani le të kujtojmë se çfarë është një logaritëm: në çfarë fuqie ju nevojitet për të ngritur bazën për të marrë argumentin? Tek e dyta. Kjo eshte:

Duket se rrënja më e vogël është e barabartë. Por kjo nuk është kështu: sipas ODZ, rrënja është e jashtme, domethënë nuk është fare rrënja e këtij ekuacioni. Kështu, ekuacioni ka vetëm një rrënjë: .

Përgjigje: .

Identiteti bazë logaritmik

Le të kujtojmë përkufizimin e logaritmit në formë të përgjithshme:

Le të zëvendësojmë logaritmin me barazinë e dytë:

Kjo barazi quhet identiteti bazë logaritmik. Edhe pse në thelb kjo është barazi - thjesht e shkruar ndryshe përkufizimi i logaritmit:

Kjo është fuqia në të cilën ju duhet të ngrini për të arritur.

Për shembull:

Zgjidh shembujt e mëposhtëm:

Shembulli 2.

Gjeni kuptimin e shprehjes.

Zgjidhja:

Le të kujtojmë rregullin nga seksioni:, domethënë, kur një fuqi ngrihet në një fuqi, eksponentët shumëzohen. Le ta zbatojmë atë:

Shembulli 3.

Vërtetoni këtë.

Zgjidhja:

Vetitë e logaritmeve

Fatkeqësisht, detyrat nuk janë gjithmonë kaq të thjeshta - shpesh së pari duhet të thjeshtoni shprehjen, ta sillni atë në formën e saj të zakonshme dhe vetëm atëherë do të jetë e mundur të llogaritni vlerën. Kjo është më e lehtë për ta bërë nëse e dini vetitë e logaritmeve. Pra, le të mësojmë vetitë themelore të logaritmeve. Unë do të vërtetoj secilën prej tyre, sepse çdo rregull është më i lehtë për t'u mbajtur mend nëse e dini se nga vjen.

Të gjitha këto veti duhet të mbahen mend pa to, shumica e problemeve me logaritme nuk mund të zgjidhen.

Dhe tani për të gjitha vetitë e logaritmeve në më shumë detaje.

Prona 1:

Dëshmi:

Le të jetë atëherë.

Kemi: , etj.

Vetia 2: Shuma e logaritmeve

Shuma e logaritmeve me baza të njëjta është e barabartë me logaritmin e produktit: .

Dëshmi:

Le të jetë atëherë. Le të jetë atëherë.

Shembull: Gjeni kuptimin e shprehjes: .

Zgjidhja:.

Formula që sapo mësuat ndihmon për të thjeshtuar shumën e logaritmeve, jo ndryshimin, kështu që këto logaritme nuk mund të kombinohen menjëherë. Por ju mund të bëni të kundërtën - "ndani" logaritmin e parë në dy: Dhe këtu është thjeshtimi i premtuar:
.
Pse është e nevojshme kjo? Epo, për shembull: çfarë është e barabartë?

Tani është e qartë se.

Tani thjeshtoje vetë:

Detyrat:

Përgjigjet:

Vetia 3: Diferenca e logaritmeve:

Dëshmi:

Gjithçka është saktësisht e njëjtë si në pikën 2:

Le të jetë atëherë.

Le të jetë atëherë. Ne kemi:

Shembulli nga paragrafi i mëparshëm tani bëhet edhe më i thjeshtë:

Një shembull më i ndërlikuar: . A mund të kuptoni se si ta zgjidhni vetë?

Këtu duhet theksuar se nuk kemi një formulë të vetme për logaritmet në katror. Kjo është diçka e ngjashme me një shprehje - nuk mund të thjeshtohet menjëherë.

Prandaj, le të bëjmë një pushim nga formulat për logaritmet dhe të mendojmë se çfarë lloj formulash përdorim më shpesh në matematikë? Që në klasën e 7-të!

Kjo -. Ju duhet të mësoheni me faktin se ata janë kudo! Ato ndodhin në probleme eksponenciale, trigonometrike dhe irracionale. Prandaj, ato duhet të mbahen mend.

Nëse shikoni nga afër dy termat e parë, bëhet e qartë se kjo dallimi i katrorëve:

Përgjigja për të kontrolluar:

Thjeshtoje vetë.

Shembuj

Përgjigjet.

Vetia 4: Marrja e eksponentit nga argumenti i logaritmit:

Dëshmi: Dhe këtu përdorim edhe përkufizimin e logaritmit: le, atëherë. Kemi: , etj.

Ky rregull mund të kuptohet në këtë mënyrë:

Kjo do të thotë, shkalla e argumentit zhvendoset përpara logaritmit si koeficient.

Shembull: Gjeni kuptimin e shprehjes.

Zgjidhja: .

Vendosni vetë:

Shembuj:

Përgjigjet:

Vetia 5: Marrja e eksponentit nga baza e logaritmit:

Dëshmi: Le të jetë atëherë.

Kemi: , etj.
Mbani mend: nga bazat shkalla shprehet si e kundërta numër, ndryshe nga rasti i mëparshëm!

Vetia 6: Heqja e eksponentit nga baza dhe argumenti i logaritmit:

Ose nëse gradat janë të njëjta: .

Prona 7: Kalimi në një bazë të re:

Dëshmi: Le të jetë atëherë.

Kemi: , etj.

Vetia 8: Ndërroni bazën dhe argumentin e logaritmit:

Dëshmi: Ky është një rast i veçantë i formulës 7: nëse zëvendësojmë, marrim: , etj.

Le të shohim disa shembuj të tjerë.

Shembulli 4.

Gjeni kuptimin e shprehjes.

Ne përdorim vetitë e logaritmeve nr. 2 - shuma e logaritmeve me të njëjtën bazë është e barabartë me logaritmin e produktit:

Shembulli 5.

Gjeni kuptimin e shprehjes.

Zgjidhja:

Ne përdorim vetinë e logaritmeve nr.3 dhe nr.4:

Shembulli 6.

Gjeni kuptimin e shprehjes.

Zgjidhja:

Le të përdorim vetinë nr. 7 - kalojmë në bazën 2:

Shembulli 7.

Gjeni kuptimin e shprehjes.

Zgjidhja:

Si ju pëlqen artikulli?

Nëse jeni duke lexuar këto rreshta, atëherë keni lexuar të gjithë artikullin.

Dhe kjo është e lezetshme!

Tani na tregoni si ju pëlqen artikulli?

A keni mësuar si të zgjidhni logaritmet? Nëse jo, cili është problemi?

Na shkruani në komentet më poshtë.

Dhe, po, fat të mirë në provimet tuaja.

Për Provimin e Bashkuar të Shtetit dhe Provimin e Bashkuar të Shtetit dhe në jetë në përgjithësi

Logaritmi numër pozitiv N në bazë(b> 0, b 1 ) i quajtur eksponent x , në të cilën ju duhet të ndërtoni b për të marrë N .

Shënimi i logaritmit:

Kjo hyrje është e barabartë me sa vijon:b x = N .

SHEMBUJ: regjistri 3 81 = 4, pasi 3 4 = 81;

Regjistri 1/3 27 = – 3, pasi (1/3) - 3 = 3 3 = 27.

Përkufizimi i mësipërm i logaritmit mund të shkruhet si një identitet:

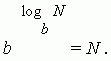
Vetitë themelore të logaritmeve.

1) log b= 1 , sepse b 1 = b.

b

2) log 1 = 0 , sepse b 0 = 1 .

b

3) Logaritmi i produktit është i barabartë me shumën e logaritmeve të faktorëve:

log( ab) = log a+ log b.

4) Logaritmi i herësit është i barabartë me diferencën midis logaritmeve të dividendit dhe pjesëtuesit:

log( a/b) = log a– regjistër b.

5) Logaritmi i një fuqie është i barabartë me produktin e eksponentit dhe logaritmin e bazës së tij:

log (b k ) = k log b.

Pasoja e kësaj prone është si më poshtë:logaritmi i rrënjës e barabartë me logaritmin e numrit radikal të pjesëtuar me fuqinë e rrënjës:

6) Nëse baza e logaritmit është një shkallë, atëherë vlera inversi i eksponentit, mund të hiqet nga shenja log rima:

Dy vetitë e fundit mund të kombinohen në një:

7) Formula e modulit të tranzicionit (d.m.th. e . kalimi nga një bazëlogaritmi në një bazë tjetër):

Në rastin e veçantë kur N=a ne kemi:

Logaritmi dhjetor thirrur logaritmi bazë 10. Është caktuar lg, d.m.th. regjistri 10 N = lg N. Logaritmet e numrave 10, 100, 1000, ... fq numrat janë përkatësisht 1, 2, 3, ...ato.

kanë kaq shumë pozitive njësi, sa zero ka një numër logaritmik pas një. Logaritmet e numrave 0.1, 0.01, 0.001, ... fq –2, –3, …, d.m.th. kanë aq negative sa ka zero para një në numrin logaritmik ( duke numëruar dhe zero numra të plotë). Logaritmet numrat e tjerë kanë një pjesë thyesore të quajtur mantisa. E tërëquhet një pjesë e logaritmit karakteristike. Për përdorim praktikLogaritmet dhjetore janë më të përshtatshmet.

Logaritmi natyror thirrur logaritmi bazë e. Është caktuar ln, d.m.th. log eN = ln N. Numri eështë irracionale, ështëvlera e përafërt 2.718281828. Ajo është kufiri në të cilin priret numri(1 + 1 / n) n me rritje të pakufizuarn(cm. kufiri i parë i mrekullueshëm ).
Sado e çuditshme mund të duket, logaritmet natyrore rezultuan të ishin shumë të përshtatshëm kur kryenin lloje të ndryshme operacionesh që lidhen me analizën e funksioneve.Llogaritja e logaritmeve në bazëekryhet shumë më shpejt se për çdo arsye tjetër.