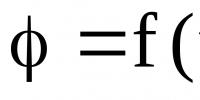Lineární faktorizační vzorec. Lineární rozklad některých čtvercových trinomů

Je uvedeno 8 příkladů faktorizace polynomů. Zahrnují příklady s řešením kvadratických a bikvadratických rovnic, příklady s opakujícími se polynomy a příklady s hledáním celých kořenů polynomů třetího a čtvrtého stupně.

Obsah

Viz také: Metody faktorizace polynomů
Kořeny kvadratické rovnice
Řešení kubických rovnic

1. Příklady s řešením kvadratické rovnice

Příklad 1.1

X 4 + x 3 - 6 x 2.

Vyjměte x 2 pro závorky:
.
2 + x - 6 = 0:
.
Kořeny rovnic:
, .

.

Příklad 1.2

Rozložení polynomu třetího stupně:
X 3 + 6 x 2 + 9 x.

Vyjmeme x ze závorek:
.
Řešíme kvadratickou rovnici x 2 + 6 x + 9 = 0:
Jeho diskriminant je .
Protože diskriminant je roven nule, kořeny rovnice jsou násobky: ;
.

Odtud získáme rozklad polynomu na faktory:
.

Příklad 1.3

Rozložení polynomu pátého stupně:
X 5 – 2 x 4 + 10 x 3.

Vyjměte x 3 pro závorky:
.
Řešíme kvadratickou rovnici x 2 - 2 x + 10 = 0.
Jeho diskriminant je .
Protože diskriminant je menší než nula, kořeny rovnice jsou složité: ;
, .

Faktorizace polynomu má tvar:
.

Pokud nás zajímá faktoring s reálnými koeficienty, pak:
.

Příklady faktorizace polynomů pomocí vzorců

Příklady s bikvadratickými polynomy

Příklad 2.1

Rozložte bikvadratický polynom na faktor:
X 4 + x 2 - 20.

Použijte vzorce:
A 2 + 2 ab + b 2 = (a + b) 2;
A 2 - b 2 = (a - b) (a + b).

;
.

Příklad 2.2

Rozložení polynomu, který se redukuje na bikvadratický:
X 8 + x 4 + 1.

Použijte vzorce:
A 2 + 2 ab + b 2 = (a + b) 2;
A 2 - b 2 = (a - b) (a + b):

;

;
.

Příklad 2.3 s rekurzivním polynomem

Faktorizace rekurzivního polynomu:
.

Rekurzivní polynom má lichý stupeň. Proto má kořen x = - 1 . Polynom dělíme x - (-1) = x + 1. V důsledku toho získáme:
.
Provádíme náhradu:
, ;
;


;
.

Příklady faktoringu polynomů s celočíselnými kořeny

Příklad 3.1

Rozložení polynomu:
.

Předpokládejme rovnici

6
-6, -3, -2, -1, 1, 2, 3, 6 .
(-6) 3 - 6 (-6) 2 + 11 (-6) - 6 = -504;
(-3) 3 - 6 (-3) 2 + 11 (-3) - 6 = -120;
(-2) 3 - 6 (-2) 2 + 11 (-2) - 6 = -60;
(-1) 3 - 6 (-1) 2 + 11 (-1) - 6 = -24;
1 3 - 6 1 2 + 11 1 - 6 = 0;
2 3 - 6 2 2 + 11 2 - 6 = 0;
3 3 - 6 3 2 + 11 3 - 6 = 0;
6 3 - 6 6 2 + 11 6 - 6 = 60.

Našli jsme tedy tři kořeny:
X 1 = 1 , X 2 = 2 , X 3 = 3 .
Protože původní polynom je třetího stupně, nemá více než tři kořeny. Protože jsme našli tři kořeny, jsou jednoduché. Pak
.

Příklad 3.2

Rozložení polynomu:
.

Předpokládejme rovnici

má alespoň jeden kořen celého čísla. Pak je to dělitel čísla 2 (člen bez x ). To znamená, že celý kořen může být jedno z čísel:
-2, -1, 1, 2 .
Nahraďte tyto hodnoty jednu po druhé:
(-2) 4 + 2 (-2) 3 + 3 (-2) 3 + 4 (-2) + 2 = 6 ;
(-1) 4 + 2 (-1) 3 + 3 (-1) 3 + 4 (-1) + 2 = 0 ;
1 4 + 2 1 3 + 3 1 3 + 4 1 + 2 = 12;
2 4 + 2 2 3 + 3 2 3 + 4 2 + 2 = 54.

Takže jsme našli jeden kořen:
X 1 = -1 .
Polynom dělíme x - x 1 = x - (-1) = x + 1:


Pak,
.

Nyní musíme vyřešit rovnici třetího stupně:
.
Pokud předpokládáme, že tato rovnice má celočíselný kořen, pak je to dělitel čísla 2 (člen bez x ). To znamená, že celý kořen může být jedno z čísel:
1, 2, -1, -2 .
Nahraďte x = -1 :
.

Takže jsme našli další kořen x 2 = -1 . Bylo by možné, stejně jako v předchozím případě, rozdělit polynom , ale seskupíme členy:
.

ČTVERCOVÝ TRIPON III

§ 54. Rozklad čtvercové trojčlenky na lineární činitele

V této části uvažujeme o následující otázce: v tom případě čtvercový trinom sekera 2 + bx+c může být reprezentován jako produkt

(A 1 x+b 1) (A 2 x+b 2)

dvě relativně lineární X faktory s reálnými koeficienty A 1 , b 1 , A 2 , b 2 (A 1 =/=0, A 2 =/=0) ?

1. Předpokládejme, že daný čtvercový trojčlen sekera 2 + bx+c reprezentovat ve formě

sekera 2 + bx+c = (A 1 x+b 1) (A 2 x+b 2). (1)

Pravá strana vzorce (1) zmizí, když X = - b 1 / A 1 a X = - b 2 / A 2 (A 1 a A 2 se podle podmínky nerovnají nule). Ale v tomto případě čísla b 1 / A 1 a - b 2 / A 2 jsou kořeny rovnice

sekera 2 + bx+c = 0.

Tedy diskriminant čtvercového trojčlenu sekera 2 + bx+c musí být nezáporné.

2. A naopak předpokládejme, že diskriminant D = b 2 - 4eso čtvercový trojčlen sekera 2 + bx+c není negativní. Pak má tento trinom skutečné kořeny X 1 a X 2. Pomocí Vieta teorému dostaneme:

sekera 2 + bx+c =A (X 2 + b / A X + C / A ) = A [X 2 - (X 1 + X 2) X + X 1 X 2 ] =

= A [(X 2 - X 1 X ) - (X 2 X - X 1 X 2)] = A [X (X - X 1) - X 2 (X - X 1) =

=A (X - X 1)(X - X 2).

sekera 2 + bx+c = A (X - X 1)(X - X 2), (2)

kde X 1 a X 2 - kořeny trojčlenu sekera 2 + bx+c . Součinitel A lze přičíst jednomu ze dvou lineárních faktorů, např.

A (X - X 1)(X - X 2) = (ach - sekera 1)(X - X 2).

To ale znamená, že v posuzovaném případě čtvercový trojčlen sekera 2 + bx+c reprezentovat jako součin dvou lineárních faktorů s reálnými koeficienty.

Spojením výsledků získaných v sekcích 1 a 2 dojdeme k následující větě.

Teorém. Čtvercový trojčlen sekera 2 + bx+c pak a teprve potom lze reprezentovat jako součin dvou lineárních faktorů s reálnými koeficienty,

sekera 2 + bx+c = (ach - sekera 1)(X - X 2),

když je diskriminant tohoto čtvercového trinomu nezáporný (to znamená, když má tento trinom skutečné kořeny).

Příklad 1. Faktorizujte na lineární faktory 6 X 2 - X -1.

Kořeny tohoto čtvercového trojčlenu jsou X 1 = 1/2 a X 2 = - 1 / 3 .

Proto podle vzorce (2)

6X 2 - X -1 = 6 (X - 1 / 2)(X + 1 / 3) = (2X - 1) (3X + 1).

Příklad 2. Faktorizujte na lineární faktory X 2 + X + 1. Diskriminant tohoto čtvercového trinomu je záporný:

D = 1 2 - 4 1 1 = - 3< 0.

Tento čtvercový trinom proto nelze rozložit na lineární faktory s reálnými koeficienty.

Cvičení

Rozbalte následující výrazy na lineární faktory (č. 403 - 406):

403. 6X 2 - 7X + 2. 405. X 2 - X + 1.

404. 2X 2 - 7Ach + 6A 2 . 406. X 2 - 3Ach + 2A 2 - ab - b 2 .

Snížit zlomky (č. 407, 408):

Řešte rovnice:

Čtvercová trojčlenka může být rozdělena takto:

A x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2)

kde a je číslo, koeficient před nejvyšším koeficientem,

x je proměnná (tj. písmeno),

x 1 a x 2 - čísla, kořeny kvadratické rovnice a x 2 + b x + c \u003d 0, které se nalézají přes diskriminant.

Pokud má kvadratická rovnice pouze jeden kořen, pak expanze vypadá takto:

a x 2 + b x + c = a ⋅ (x − x 0) 2

Příklady rozkladu čtvercového trojčlenu:

1. − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1,   x 2 = 7

− x 2 + 6 x + 7 = (− 1) ⋅ (x − (− 1)) (x − 7) = − (x + 1) (x − 7) = (x + 1) (7 − x)

1. − x 2 + 4 x − 4 = 0; ⇒ x0 = 2

− x 2 + 4 x − 4 = (− 1) ⋅ (x − 2) 2 = − (x − 2) 2

Pokud je čtvercová trojčlenka neúplná (b = 0 nebo c = 0), lze ji rozložit následujícími způsoby:

• c = 0 ⇒ a x 2 + b x = x (a x + b)

• b = 0 ⇒ použijte redukovaný vzorec pro násobení rozdílu čtverců.

Úkoly pro samostatné řešení

Č.1. Čtvercový trojčlen se rozloží na faktor: x 2 + 6 x - 27 = (x + 9) (x - a) . Najdi .

Řešení:

Nejprve musíte přirovnat čtvercový trojčlen k nule, abyste našli x 1 a x 2.

x 2 + 6 x − 27 = 0

a = 1, b = 6, c = − 27

D = b 2 − 4 a c = 6 2 − 4 ⋅ 1 ⋅ (− 27) = 36 + 108 = 144

D > 0 znamená, že budou existovat dva různé kořeny.

x 1,2 = − b ± D 2 a = − 6 ± 144 2 ⋅ 1 = [ − 6 + 12 2 = 6 2 = 3 − 6 − 12 2 = − 18 2 = − 9

Když známe kořeny, rozložíme čtvercový trinom:

x 2 + 6 x − 27 = (x − (− 9)) (x − 3) = (x + 9) (x − 3)

č. 2 Rovnice x 2 + p x + q \u003d 0 má kořeny - 5; 7. Najděte q.

Řešení:

1 způsob:(potřebujete vědět, jak se skládá čtvercová trojčlenka)

Jsou-li x 1 a x 2 kořeny čtvercového trinomu a x 2 + b x + c, pak to lze rozložit následovně: a x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2) .

Protože v daném čtvercovém trinomu je vedoucí koeficient (faktor před x 2) roven jedné, bude rozklad následující:

x 2 + p x + q = (x − x 1) (x − x 2) = (x − (− 5)) (x − 7) = (x + 5) (x − 7) = x 2 − 7 x + 5 x - 35 = x 2 - 2 x - 35

x 2 + p x + q = x 2 − 2 x − 35 ⇒ p = − 2, q = − 35

2 způsob: (potřebujete znát větu Vieta)

Vietin teorém:

Součet odmocnin redukovaného čtvercového trinomu x 2 + p x + q je roven jeho druhému koeficientu p s opačným znaménkem a součin je roven volnému členu q.

( x 1 + x 2 = − p x 1 ⋅ x 2 = q

q = x 1 ⋅ x 2 = (− 5) ⋅ 7 = − 35.

Nejprve si poukažme na některé běžně používané názvy. Uvažujme polynomy, které obsahují pouze jedno písmeno, například písmeno x. Nejjednodušší je pak polynom, ve kterém jsou dva členy a jeden z nich obsahuje písmeno x do prvního stupně a druhý nemá písmeno x vůbec, například 3x - 5 nebo 15 - 7x nebo 8z + 7 (zde se místo písmene x bere písmeno z) atd. Takové polynomy se nazývají lineární binomy .

3x² - 5x + 7 nebo x² + 2x - 1
nebo 5y² + 7y + 8 nebo z² - 5z - 2 atd.

Takové polynomy se nazývají čtvercové trojčleny.

Pak můžeme sestavit krychlový čtyřnásobek, například:

x³ + 2x² - x + 1 nebo 3x³ - 5x² - 2x - 3 atd.,

polynom čtvrtého stupně, například:

x 4 - 2x³ - 3x² + 4x - 5 atd.

Koeficienty v x, x², x3 atd. je možné označovat také písmeny, například písmeny a, b, c atd. Pak dostaneme:

1) obecný tvar binomického lineárního v x ax + b,

2) obecný tvar čtvercového trinomu (vzhledem k x): ax² + bx + c,

3) obecný tvar kubického trinomu (vzhledem k x): ax³ + bx² + cx + d atd.

Nahrazením písmen a, b, c, d ... v těchto vzorcích různými čísly získáme všechny druhy lineárních dvojčlenů, čtvercových trojčlenů atd. Například ve vzorci ax² + bx + c, který vyjadřuje obecný tvar čtvercového trinomu nahradíme písmeno a číslem + 3, písmeno b číslem -2 a písmeno c číslem -1, dostaneme čtvercový trojčlen 3x² - 2x - 1. V konkrétním případě, je také možné získat binom, který nahradí jedno z písmen nulou, například pokud a = +1, b = 0 a c \u003d -3, dostaneme čtvercový binom x² - 3.

Některé čtvercové trinomy se lze naučit faktorizovat poměrně rychle na lineární faktory. My se však omezíme na zvážení pouze takových čtvercových trinomů, které splňují následující podmínky:

1) koeficient v nejvyšším členu (při x²) je +1,

2) lze najít dvě celá čísla (se znaménkem nebo dvě relativní celá čísla) taková, že jejich součet se rovná koeficientu x k první mocnině a jejich součin je roven členu bez x (kde není písmeno x na Všechno).

Příklady. 1. x² + 5x + 6; v mysli je snadné najít dvě čísla (se znaménkem) tak, aby jejich součet byl roven +5 (koeficient v x) a aby jejich součin = +6 (člen prostý x), - tato čísla jsou: + 2 a +3 [sám o sobě ve skutečnosti +2 + 3 = +5 a (+2) ∙ (+3) = +6]. Pomocí těchto dvou čísel nahradíme člen +5x dvěma členy, a to: +2x + 3x (samozřejmě +2x + 3x = +5x); pak bude náš technický termín uměle převeden na čtyřnásobek x² + 2x + 3x + 6. Aplikujme na něj nyní techniku ​​seskupování, přičemž první dva termíny umístíme do jedné skupiny a poslední dva do jiné:

x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).

V první skupině jsme uzavřeli x a ve druhé +3 jsme dostali dva členy, které měly společný faktor (x + 2), který byl také uzavřen, a náš trinom x² + 5x + 6 se rozložil na 2 lineární faktory: x + 2 a x + 3.

2. x² - x - 12. Zde musíte najít dvě čísla (relativní), aby jejich součet byl -1 a aby jejich součin byl -12. Taková čísla jsou: -4 a +3.

Zkontrolujte: -4 + 3 = -1; (-4) (+3) = -12. Pomocí těchto čísel nahradíme člen -x dvěma členy: -x \u003d -4x + 3x, - dostaneme:

x² - x - 12 \u003d x² - 4x + 3x - 12 \u003d x (x - 4) + 3 (x - 4) \u003d (x - 4) (x + 3).

3. x² - 7x + 6; zde jsou požadovaná čísla: -6 a -1. [Kontrola: -6 + (-1) = -7; (–6) (–1) = +6].

x² - 7x + 6 = x² - 6x - x + 6 = x (x - 6) - (x - 6) = (x - 6) (x - 1).

Zde bylo nutné členy druhé skupiny -x + 6 uzavřít do závorek se znaménkem mínus před nimi.

4. x² + 8x - 48. Zde musíte najít dvě čísla tak, aby jejich součet byl +8 a součin -48. Protože součin musí mít znaménko mínus, pak požadovaná čísla musí mít různá znaménka, protože součet našich čísel má znaménko +, pak absolutní hodnota kladné číslo by mělo být více. Rozložením aritmetického čísla 48 na dva faktory (a to lze provést různými způsoby) dostaneme: 48 = 1 ∙ 48 = 2 ∙ 24 = 3 ∙ 16 = 4 ∙ 12 = 6 ∙ 8. , konkrétně: 48 = 4 ∙ 12. Pak jsou naše čísla: +12 a -4. Následuje jednoduché:

x² + 8x - 48 = x² + 12x - 4x - 48 = x (x + 12) - 4 (x + 12) = (x + 12) (x - 4).

5. x² + 7x - 12. Zde musíte najít 2 čísla tak, aby jejich součet byl +7 a součin = -12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. Zřejmě by byla vhodná čísla 3 a 4, ale je třeba je brát s různými znaménky, aby se jejich součin rovnal -12, a pak jejich součet v žádném případě není může být +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Jiné rozklady také nedávají požadovaná čísla; proto docházíme k závěru, že tyto čtvercové trinomy zatím nejsme schopni rozložit na lineární faktory, protože naše metoda na ně není použitelná (nesplňuje druhou z podmínek, které byly stanoveny na začátku).

Má čtverec a skládá se ze tří členů (). Takže to dopadá - čtvercový trojčlen.

Příklady nečtvercové trojčleny:

\(x^3-3x^2-5x+6\) - kubický kvartér
\(2x+1\) - lineární binom

Odmocnina čtvercového trojčlenu:

Příklad:
Trojčlen \(x^2-2x+1\) má kořen \(1\), protože \(1^2-2 1+1=0\)
Trojčlen \(x^2+2x-3\) má kořeny \(1\) a \(-3\), protože \(1^2+2-3=0\) a \((-3)^ 2-6-3=9-9=0\)

Například: pokud potřebujete najít kořeny pro čtvercový trinom \(x^2-2x+1\), přirovnáme jej k nule a vyřešíme rovnici \(x^2-2x+1=0\).

\(D=4-4\cdot1=0\)
\(x=\frac(2-0)(2)=\frac(2)(2)=1\)

Připraveno. Kořen je \(1\).

Rozklad čtvercového trojčlenu na:

Čtvercový trojčlen \(ax^2+bx+c\) lze rozšířit jako \(a(x-x_1)(x-x_2)\), pokud jsou rovnice \(ax^2+bx+c=0\) větší než nula \ (x_1\) a \(x_2\) jsou kořeny stejné rovnice).

Například, zvažte trinom \(3x^2+13x-10\).
Kvadratická rovnice \(3x^2+13x-10=0\) má diskriminant rovný 289 (větší než nula) a kořeny jsou rovny \(-5\) a \(\frac(2)(3 )\). Takže \(3x^2+13x-10=3(x+5)(x-\frac(2)(3))\). Ověřit správnost tohoto tvrzení je snadné – pokud budeme , pak dostaneme původní trojčlenku.

Čtvercový trojčlen \(ax^2+bx+c\) může být reprezentován jako \(a(x-x_1)^2\), pokud je diskriminant rovnice \(ax^2+bx+c=0\) rovna nule.

Například, zvažte trinom \(x^2+6x+9\).
Kvadratická rovnice \(x^2+6x+9=0\) má diskriminant roven \(0\) a jediný kořen je roven \(-3\). Takže, \(x^2+6x+9=(x+3)^2\) (zde koeficient \(a=1\), takže není třeba psát před závorku). Vezměte prosím na vědomí, že stejnou transformaci lze provést pomocí .

Čtvercová trojčlenka \(ax^2+bx+c\) nefaktorizuje, pokud je diskriminant rovnice \(ax^2+bx+c=0\) menší než nula.

Například, trinomy \(x^2+x+4\) a \(-5x^2+2x-1\) mají diskriminant menší než nula. Proto je nemožné je rozložit na faktory.

Příklad . Faktor \(2x^2-11x+12\).
Řešení :
Najděte kořeny kvadratické rovnice \(2x^2-11x+12=0\)

\(D=11^2-4 \cdot 2 \cdot 12=121-96=25>0\)
\(x_1=\frac(11-5)(4)=1,5;\) \(x_2=\frac(11+5)(4)=4.\)

Takže \(2x^2-11x+12=2(x-1,5)(x-4)\)
Odpovědět : \(2(x-1,5)(x-4)\)

Přijatá odpověď může být zapsána jiným způsobem: \((2x-3)(x-4)\).

Příklad . (Úkol od OGE)Čtvercová trojčlenka je rozložena \(5x^2+33x+40=5(x++ 5)(x-a)\). Najdi\).
Řešení:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac(-33-17)(10)=-5\)
\(x_2=\frac(-33+17)(10)=-1,6\)
\(5x^2+33x+40=5(x+5)(x+1,6)\)
Odpovědět : \(-1,6\)