El término (módulo) traducido literalmente del latín significa "medida". Este concepto fue introducido en las matemáticas por el científico inglés R. Cotes. Y el matemático alemán K. Weierstrass introdujo el signo del módulo, un símbolo que denota este concepto al escribir.

En contacto con

Por primera vez se estudia este concepto en matemáticas en el currículo de 6º grado de secundaria. Según una definición, el módulo es el valor absoluto de un número real. En otras palabras, para averiguar el módulo de un número real, es necesario descartar su signo.

Valor gráfico absoluto A denotado como |un|.

Principal característica distintiva Este concepto es que siempre es una cantidad no negativa.

Los números que sólo difieren entre sí en el signo se llaman números opuestos. Si un valor es positivo, entonces su opuesto es negativo y cero es su opuesto.

Significado geométrico

Si consideramos el concepto de módulo desde el punto de vista de la geometría, entonces denotará la distancia que se mide en segmentos unitarios desde el origen de coordenadas hasta Punto dado. Esta definición revela plenamente significado geométrico el término que se estudia.

Gráficamente esto se puede expresar de la siguiente manera: |a| = OA.

Propiedades del valor absoluto

A continuación consideraremos todas las propiedades matemáticas de este concepto y las formas de escribirlo en forma de expresiones literales:

Características de resolver ecuaciones con módulo.

Si hablamos de resolver ecuaciones matemáticas y desigualdades que contienen módulo, entonces debemos recordar que para resolverlas será necesario abrir este signo.

Por ejemplo, si el signo de un valor absoluto contiene alguna expresión matemática, antes de abrir el módulo es necesario tener en cuenta las definiciones matemáticas actuales.

|A+5| = A + 5, si A es mayor o igual a cero.

5-A, si, un valor es menor que cero.

En algunos casos, el signo puede revelarse de forma inequívoca para cualquier valor de la variable.

Veamos otro ejemplo. Construyamos una línea de coordenadas en la que marcamos todos los valores numéricos cuyo valor absoluto será 5.

Primero necesitas dibujar una línea de coordenadas, marcar el origen de las coordenadas en ella y establecer el tamaño de un segmento unitario. Además, la línea recta debe tener una dirección. Ahora, en esta línea es necesario aplicar marcas que serán iguales al tamaño de un segmento unitario.

Así, podemos ver que sobre esta línea de coordenadas habrá dos puntos de nuestro interés con valores 5 y -5.

Escuela secundaria MBOU nº 17, Ivanovo

« Ecuaciones con módulo"
Desarrollo metodológico

compilado

profesor de matemáticas

Lebedeva N.V.

20010

Nota explicativa

Capítulo 1 Introducción

Sección 2. Propiedades básicas Sección 3. Interpretación geométrica del concepto de módulo de un número Sección 4. Gráfica de la función y = |x| Sección 5. Convenciones

Capítulo 2. Resolver ecuaciones que contienen un módulo.

Sección 1. Ecuaciones de la forma |F(x)| = m (más simple) Sección 2. Ecuaciones de la forma F(|x|) = m Sección 3. Ecuaciones de la forma |F(x)| = G(x) Sección 4. Ecuaciones de la forma |F(x)| = ± F(x) (más bella) Sección 5. Ecuaciones de la forma |F(x)| = |G(x)| Sección 6. Ejemplos de resolución de ecuaciones no estándar. Sección 7. Ecuaciones de la forma |F(x)| + |G(x)| = 0 Sección 8. Ecuaciones de la forma |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± en n | = metro Sección 9. Ecuaciones que contienen varios módulos.

Capítulo 3. Ejemplos de resolución de varias ecuaciones con módulo.

Sección 1. Ecuaciones trigonométricas Sección 2. Ecuaciones exponenciales Seccion 3. Ecuaciones logarítmicas Sección 4. Ecuaciones irracionales Sección 5. Tareas avanzadas Respuestas a los ejercicios. Bibliografía

Nota explicativa.

El concepto de valor absoluto (módulo) de un número real es una de sus características esenciales. Este concepto está muy extendido en diversas ramas de las ciencias físicas, matemáticas y técnicas. En la práctica de enseñar cursos de matemáticas en escuela secundaria de acuerdo con el Programa del Ministerio de Defensa de la Federación de Rusia, el concepto de "valor absoluto de un número" se encuentra repetidamente: en sexto grado, se introduce la definición de módulo y su significado geométrico; en octavo grado se forma el concepto error absoluto, se considera la solución de las ecuaciones y desigualdades más simples que contienen un módulo, se estudian las propiedades de la aritmética raíz cuadrada; en 11º grado el concepto se encuentra en la sección “Raíz norte-ésimo grado." La experiencia docente demuestra que los estudiantes suelen encontrar dificultades para resolver tareas que requieren conocimiento de este material, y muchas veces se las saltan sin empezar a completarlas. Los textos de los exámenes de los cursos de 9º y 11º grado también incluyen tareas similares. Además, los requisitos que las universidades imponen a los graduados escolares difieren, a saber, más nivel alto que los requisitos del plan de estudios escolar. Para la vida en sociedad moderna Es muy importante desarrollar un estilo de pensamiento matemático, que se manifieste en determinadas habilidades mentales. En el proceso de resolución de problemas con módulos se requiere la capacidad de utilizar técnicas como generalización y especificación, análisis, clasificación y sistematización, y analogía. Resolver estas tareas le permite poner a prueba su conocimiento de las secciones principales. curso escolar, nivel pensamiento lógico, habilidades iniciales de investigación. Este trabajo está dedicado a una de las secciones: la resolución de ecuaciones que contienen el módulo. Consiste en tres capítulos. El primer capítulo introduce los conceptos básicos y las consideraciones teóricas más importantes. El segundo capítulo propone nueve tipos principales de ecuaciones que contienen un módulo, analiza métodos para resolverlas y examina ejemplos de diferentes niveles de complejidad. El tercer capítulo ofrece ecuaciones más complejas y no estándar (trigonométricas, exponenciales, logarítmicas e irracionales). Para cada tipo de ecuación hay ejercicios para decisión independiente(Se adjuntan respuestas e instrucciones). El objetivo principal de este trabajo es brindar asistencia metodológica a los docentes en la preparación de las lecciones y en la organización de cursos optativos. El material también se puede utilizar como ayuda para enseñar para estudiantes de secundaria. Las tareas propuestas en el trabajo son interesantes y no siempre fáciles de resolver, lo que permite concienciar la motivación educativa de los estudiantes, poner a prueba sus habilidades y aumentar el nivel de preparación de los graduados escolares para ingresar a las universidades. Una selección diferenciada de los ejercicios propuestos implica una transición del nivel reproductivo de dominio del material al creativo, así como la oportunidad de enseñar cómo aplicar sus conocimientos a la hora de resolver problemas atípicos.

Capítulo 1 Introducción.

Sección 1. Determinación del valor absoluto .

Definición : El valor absoluto (módulo) de un número real. A llamado no un numero negativo: A o -A. Designación: │ A │ La entrada dice lo siguiente: “módulo del número a” o “valor absoluto del número a”

│ a, si a > 0

│a│ = │ 0, si a = 0 (1)

│ - y, si un
Ejemplos: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Expandir módulo de expresión:

a) │x - 8│, si x > 12 b) │2x + 3│, si x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Sección 2. Propiedades básicas.

Consideremos las propiedades básicas del valor absoluto. Propiedad #1: Los números opuestos tienen módulos iguales, es decir │а│=│- а│ Demostremos que la igualdad es verdadera. Anotemos la definición del número. - A : │- un│= (2) Comparemos los conjuntos (1) y (2). Es obvio que las definiciones valores absolutos números A Y - A emparejar. Por eso, │а│=│- а│
Al considerar las siguientes propiedades, nos limitaremos a su formulación, ya que su prueba se da en Propiedad #2: El valor absoluto de la suma de un número finito de números reales no excede la suma de los valores absolutos de los términos: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Propiedad #3: El valor absoluto de la diferencia entre dos números reales no excede la suma de sus valores absolutos: │а - в│ ≤│а│+│в│ Propiedad #4: El valor absoluto del producto de un número finito de números reales es igual al producto de los valores absolutos de los factores: │а·в│=│а│·│в│ Propiedad #5: El valor absoluto del cociente de números reales es igual al cociente de sus valores absolutos:

Sección 3. Interpretación geométrica del concepto de módulo de un número.

Cada número real se puede asociar a un punto de la recta numérica, que será una imagen geométrica de este número real. Cada punto de la recta numérica corresponde a su distancia del origen, es decir la longitud del segmento desde el origen hasta un punto dado. Esta distancia siempre se considera un valor no negativo. Por tanto, la longitud del segmento correspondiente será la interpretación geométrica del valor absoluto de un número real dado.

Enviado ilustración geométrica confirma claramente la propiedad No. 1, es decir. los módulos de números opuestos son iguales. De aquí se entiende fácilmente la validez de la igualdad: │х – а│= │а – x│. La solución a la ecuación │x│= m, donde m ≥ 0, es decir, x 1,2 = ± m, también se vuelve más obvia. Ejemplos: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Sección 4. Gráfica de la función y = │x│

El dominio de esta función son todos los números reales.

Sección 5. Convenios.

En el futuro, al considerar ejemplos de resolución de ecuaciones, se utilizarán las siguientes convenciones: ( - signo del sistema [ - signo de la totalidad Al resolver un sistema de ecuaciones (desigualdades), se encuentra la intersección de las soluciones de las ecuaciones (desigualdades) incluidas en el sistema. Al resolver un conjunto de ecuaciones (desigualdades), se encuentra la unión de soluciones incluidas en el conjunto de ecuaciones (desigualdades).

Capítulo 2. Resolución de ecuaciones que contienen un módulo.

En este capítulo veremos métodos algebraicos para resolver ecuaciones que contienen uno o más módulos.

Sección 1. Ecuaciones de la forma │F (x)│= m

Una ecuación de este tipo se llama la más simple. Tiene solución si y sólo si m ≥ 0. Por definición del módulo, la ecuación original es equivalente a un conjunto de dos ecuaciones: │ F(x)│=metro
Ejemplos:
№1. Resuelve la ecuación: │7х - 2│= 9


Respuesta:x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Respuesta: la suma de las raíces es - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 denota x 2 = m, m ≥ 0 x = 0; ±√5m2 – 5m + 4 = 0m = 1; 4 – ambos valores satisfacen la condición m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Respuesta: número de raíces de la ecuación 7. Ejercicios:
№1. Resuelve la ecuación e indica la suma de las raíces: │х - 5│= 3 №2 . Resuelve la ecuación e indica la raíz más pequeña: │x 2 + x│= 0 №3 . Resuelve la ecuación e indica la raíz mayor: │x 2 – 5x + 4│= 4 №4 .Resuelve la ecuación e indica la raíz entera: │2x 2 – 7x + 6│= 1 №5 .Resolver la ecuación e indicar el número de raíces: │x 4 – 13x 2 + 50│= 14

Sección 2. Ecuaciones de la forma F(│х│) = m

El argumento de la función en el lado izquierdo está bajo el signo del módulo y el lado derecho es independiente de la variable. Consideremos dos formas de resolver ecuaciones de este tipo. 1 vía: Por definición de valor absoluto, la ecuación original equivale a la combinación de dos sistemas. En cada uno de los cuales se impone una condición a una expresión submodular. F(│х│) =metro
Dado que la función F(│x│) es par en todo el dominio de definición, las raíces de las ecuaciones F(x) = my F(- x) = m son pares de números opuestos. Por lo tanto, basta con resolver uno de los sistemas (al considerar ejemplos de esta manera, se dará la solución a un sistema). Método 2: Aplicación del método de introducción de una nueva variable. En este caso se introduce la notación │x│= a, donde a ≥ 0. Este método Menos voluminoso en diseño.
Ejemplos: №1 . Resuelve la ecuación: 3x 2 – 4│x│= - 1 Usemos la introducción de una nueva variable. Denotemos │x│= a, donde a ≥ 0. Obtenemos la ecuación 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Regresamos a la variable original: │ x│=1 y │х│= 1/3. Cada ecuación tiene dos raíces. Respuesta:x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Resuelve la ecuación: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Encontremos la solución al primer sistema de la población: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Tenga en cuenta que x 2 no satisface la condición x ≥ 0. Solución el segundo sistema será el número opuesto al valor x 1. Respuesta:x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Resolver la ecuación: x 4 – │х│= 0 Denotemos │х│= a, donde a ≥ 0. Obtenemos la ecuación a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Regresar a la variable original: │х│=0 y │х│= 1 x = 0; ± 1 Respuesta:x 1 = 0; X 2 = 1; X 3 = - 1.
Ejercicios: №6. Resuelve la ecuación: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Resuelve la ecuación, indica el número de raíces en tu respuesta: 3x 2 - 7│x│ + 2 = 0 №8 . Resuelve la ecuación, indica soluciones enteras en tu respuesta: x 4 + │x│ - 2 = 0

Sección 3. Ecuaciones de la forma │F(x)│ = G(x)

El lado derecho de una ecuación de este tipo depende de una variable y, por lo tanto, tiene solución si y sólo si el lado derecho es una función G(x) ≥ 0. La ecuación original se puede resolver de dos maneras : 1 vía: Estándar, basado en la divulgación de un módulo en función de su definición y consiste en una transición equivalente a una combinación de dos sistemas. │ F(x)│ =GRAMO(X)

Este método puede usarse racionalmente en el caso de una expresión compleja para la función G(x) y una menos compleja para la función F(x), ya que se supone que las desigualdades con la función F(x) serán resueltas. Método 2: Consiste en la transición a un sistema equivalente en el que se impone una condición en el lado derecho. │ F(X)│= GRAMO(X)

Este método es más conveniente de usar si la expresión para la función G(x) es menos compleja que para la función F(x), ya que se supone la solución a la desigualdad G(x) ≥ 0. de varios módulos, se recomienda utilizar la segunda opción. Ejemplos: №1. Resuelve la ecuación: │x + 2│= 6 -2x
(1 vía) Respuesta: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 vías) Respuesta: El producto de las raíces es 3.
№3. Resuelve la ecuación e indica la suma de las raíces en tu respuesta:
│x - 6│= x 2 - 5x + 9

Respuesta: la suma de las raíces es 4.
Ejercicios: №9. │x + 4│= - 3x №10. Resuelve la ecuación, indica el número de soluciones en tu respuesta:│x 2 + x - 1│= 2x – 1 №11 . Resuelve la ecuación, indica el producto de las raíces en tu respuesta:│x + 3│= x 2 + x – 6

Sección 4. Ecuaciones de la forma │F(x)│= F(x) y │F(x)│= - F(x)

Las ecuaciones de este tipo a veces se denominan "las más hermosas". Dado que el lado derecho de las ecuaciones depende de la variable, existen soluciones si y sólo si el lado derecho no es negativo. Por tanto, las ecuaciones originales son equivalentes a las desigualdades:
│F(x)│= F(x) F(x) ≥ 0 y │F(x)│= - F(x) F(x) Ejemplos: №1 . Resuelve la ecuación, indica la raíz entera más pequeña en tu respuesta: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 Respuesta: x = 1№2. Resuelve la ecuación, indica la longitud del intervalo en tu respuesta: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Respuesta: la longitud del espacio es 6.№3 . Resuelve la ecuación e indica el número de soluciones enteras en tu respuesta: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Respuesta: 4 soluciones completas.№4 . Resuelve la ecuación e indica la raíz más grande en tu respuesta:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Respuesta: x = 3.

Ejercicios: №12. Resuelve la ecuación, indica la raíz completa en la respuesta: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Resuelve la ecuación, indica el número de soluciones enteras en tu respuesta: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Resuelve la ecuación; en tu respuesta, indica un número entero que no sea la raíz de la ecuación:

Sección 5. Ecuaciones de la forma │F(x)│= │G(x)│

Dado que ambos lados de la ecuación no son negativos, la solución implica considerar dos casos: las expresiones submodulares son iguales o de signo opuesto. Por tanto, la ecuación original es equivalente a la combinación de dos ecuaciones: │ F(X)│= │ GRAMO(X)│
Ejemplos: №1. Resuelve la ecuación, indica la raíz completa en tu respuesta: │x + 3│=│2x - 1│
Respuesta: raíz entera x = 4.№2. Resuelve la ecuación: │ x – x 2 - 1│=│2x – 3 – x 2 │
Respuesta: x = 2.№3 . Resuelve la ecuación e indica el producto de las raíces en tu respuesta:




Ecuaciones raíz 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Respuesta: el producto de las raíces es – 0,25. Ejercicios: №15 . Resuelve la ecuación e indica la solución completa en tu respuesta: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Resuelve la ecuación, indica la raíz más pequeña en tu respuesta:│5x - 3│=│7 - x│ №17 . Resuelve la ecuación e indica la suma de las raíces en tu respuesta:

Sección 6. Ejemplos de resolución de ecuaciones no estándar.

En esta sección consideraremos ejemplos de ecuaciones no estándar, cuya resolución revela el valor absoluto de la expresión por definición. Ejemplos:

№1. Resuelve la ecuación, indica la suma de las raíces en tu respuesta: x · │x│- 5x – 6 = 0
Respuesta: la suma de las raíces es 1 №2. . Resuelve la ecuación, indica la raíz más pequeña en tu respuesta: x 2 - 4x ·
- 5 = 0
Respuesta: raíz más pequeña x = - 5. №3. Resuelve la ecuación:

Respuesta: x = -1. Ejercicios: №18. Resuelve la ecuación e indica la suma de las raíces: x · │3x + 5│= 3x 2 + 4x + 3
№19. Resuelve la ecuación: x 2 – 3x =

№20. Resuelve la ecuación:

Sección 7. Ecuaciones de la forma │F(x)│+│G(x)│=0

Es fácil notar que en el lado izquierdo de una ecuación de este tipo está la suma de cantidades no negativas. Por lo tanto, la ecuación original tiene solución si y sólo si ambos términos son iguales a cero al mismo tiempo. La ecuación es equivalente al sistema de ecuaciones: │ F(X)│+│ GRAMO(X)│=0
Ejemplos: №1 . Resuelve la ecuación:
Respuesta: x = 2. №2. Resuelve la ecuación: Respuesta: x = 1. Ejercicios: №21. Resuelve la ecuación: №22 . Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №23 . Resuelve la ecuación e indica el número de soluciones en tu respuesta:

Sección 8. Ecuaciones de la forma │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Para resolver ecuaciones de este tipo se utiliza el método del intervalo. Si lo resolvemos mediante expansión secuencial de módulos, obtenemos norte conjuntos de sistemas, lo cual es muy engorroso e inconveniente. Consideremos el algoritmo del método de intervalo: 1). Encuentra valores variables X, para lo cual cada módulo es igual a cero (ceros de expresiones submodulares):
2). Marque los valores encontrados en una recta numérica, que se divide en intervalos (el número de intervalos es respectivamente igual a norte+1 ) 3). Determine con qué signo se revela cada módulo en cada uno de los intervalos obtenidos (al hacer una solución, puede usar una recta numérica, marcando los signos en ella) 4). La ecuación original es equivalente a la suma norte+1 sistemas, en cada uno de los cuales se indica la pertenencia de la variable X uno de los intervalos. Ejemplos: №1 . Resuelve la ecuación e indica la raíz más grande en tu respuesta:
1). Encontremos los ceros de las expresiones submodulares: x = 2; x = -3 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos obtenidos:
x – 2 x – 2 x – 2 - - + - 3 2x 2x + 6 2x + 6 2x + 6 - + + 3)
- no hay soluciones La ecuación tiene dos raíces. Respuesta: la raíz más grande x = 2. №2. Resuelve la ecuación y proporciona la raíz completa en tu respuesta:
1). Encontremos los ceros de las expresiones submodulares: x = 1,5; x = - 1 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
El último sistema no tiene soluciones, por lo tanto la ecuación tiene dos raíces. Al resolver la ecuación, debes prestar atención al signo "-" delante del segundo módulo. Respuesta: raíz entera x = 7. №3. Resuelve la ecuación, indica la suma de las raíces en tu respuesta: 1). Encontremos los ceros de las expresiones submodulares: x = 5; x = 1; x = - 2 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
La ecuación tiene dos raíces x = 0 y 2. Respuesta: la suma de las raíces es 2. №4 . Resuelve la ecuación: 1). Encontremos los ceros de las expresiones submodulares: x = 1; x = 2; x = 3.2). Determinemos con qué signo se revela cada módulo en los intervalos resultantes. 3).
Combinemos las soluciones del primero. tres sistemas. Respuesta: ; x = 5.
Ejercicios: №24. Resuelve la ecuación:
№25. Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №26. Resuelve la ecuación e indica la raíz más pequeña en tu respuesta: №27. Resuelve la ecuación e indica la raíz mayor en tu respuesta:

Sección 9. Ecuaciones que contienen varios módulos.

Las ecuaciones que contienen varios módulos asumen la presencia de valores absolutos en expresiones submodulares. El principio básico para resolver ecuaciones de este tipo es la divulgación secuencial de módulos, comenzando por el "externo". Durante la solución se utilizan las técnicas comentadas en los apartados N° 1, N° 3.

Ejemplos: №1. Resuelve la ecuación:
Respuesta: x = 1; - once. №2. Resuelve la ecuación:
Respuesta: x = 0; 4; - 4. №3. Resuelve la ecuación e indica el producto de las raíces en tu respuesta:
Respuesta: el producto de las raíces es – 8. №4. Resuelve la ecuación:
Denotamos las ecuaciones de la población. (1) Y (2) y considere la solución para cada uno de ellos por separado para facilitar el diseño. Dado que ambas ecuaciones contienen más de un módulo, es más conveniente realizar una transición equivalente a conjuntos de sistemas. (1)

(2)


Respuesta:
Ejercicios: №36. Resuelve la ecuación, indica la suma de las raíces en tu respuesta: 5 │3x-5│ = 25 x №37. Resuelve la ecuación, si hay más de una raíz, indica la suma de las raíces en tu respuesta: │x + 2│ x – 3x – 10 = 1 №38. Resuelve la ecuación: 3 │2x -4│ = 9 │x│ №39. Resuelve la ecuación, en tu respuesta indica el número de raíces por: 2 │ sen x│ = √2 №40 . Resuelve la ecuación e indica el número de raíces en tu respuesta:

Sección 3. Ecuaciones logarítmicas.

Antes de resolver las siguientes ecuaciones es necesario repasar las propiedades de los logaritmos y la función logarítmica. Ejemplos: №1. Resuelve la ecuación, indica el producto de las raíces en tu respuesta: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Caso 1: si x ≥ - 1, entonces log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisface la condición x ≥ - 1 2 caso: si x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisface la condición x - 1
Respuesta: el producto de las raíces es – 15.
№2. Resuelve la ecuación, indica la suma de las raíces en tu respuesta: lg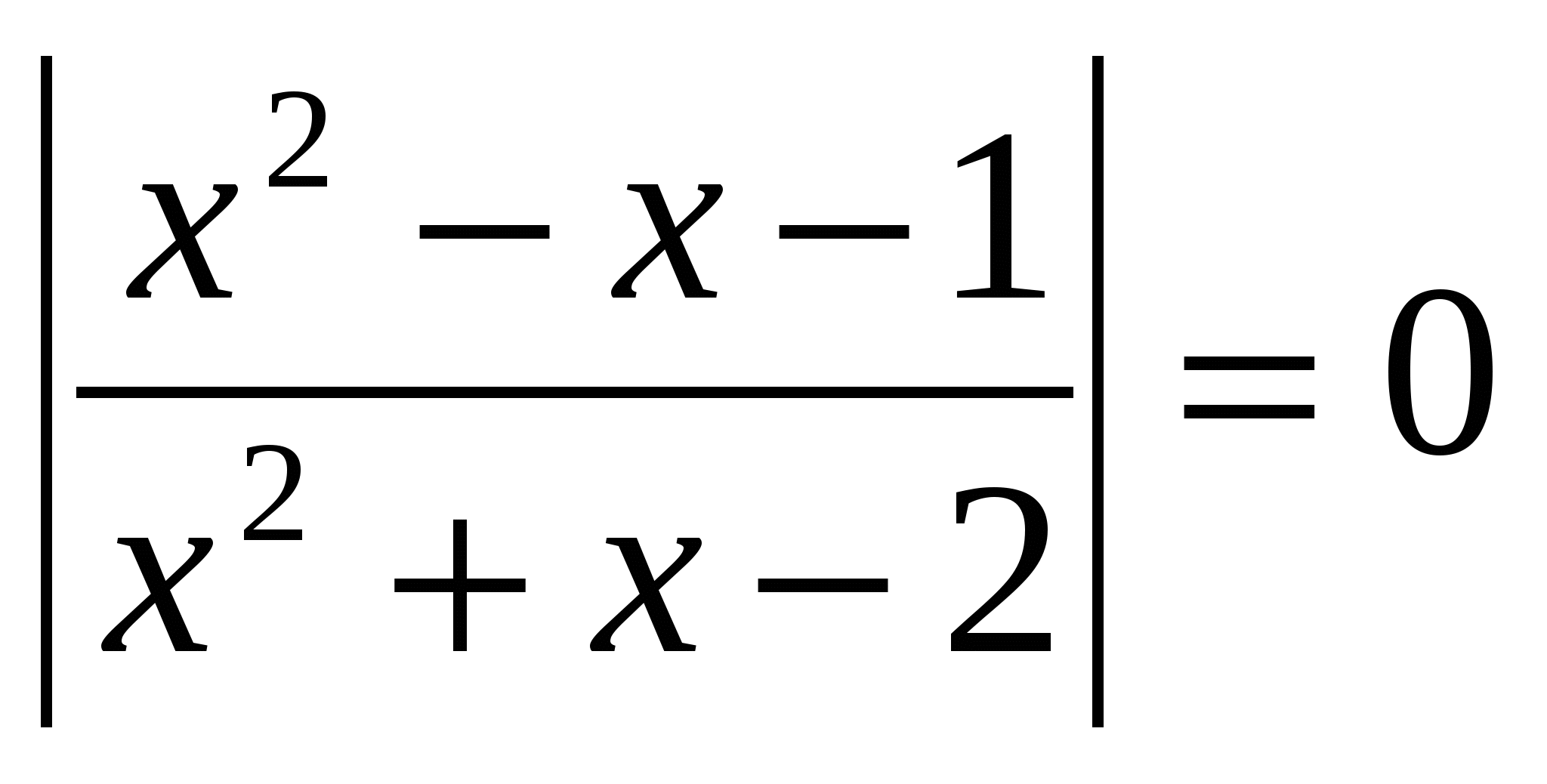
O.D.Z.

Respuesta: la suma de las raíces es 0,5.
№3. Resuelve la ecuación: log 5
O.D.Z.

Respuesta: x = 9. №4. Resuelve la ecuación: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Usemos la fórmula para pasar a otra base. │2 - iniciar sesión 5 x│+ 3 = │1 + iniciar sesión 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Encontremos los ceros de las expresiones submodulares: x = 25; x = Estos números dividen el rango de valores aceptables en tres intervalos, por lo que la ecuación equivale a un conjunto de tres sistemas.
Respuesta: )