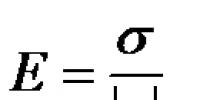Quelle est la limite de zéro ? Résoudre les problèmes liés à la recherche de limites

Solution limites des fonctions en ligne. Trouver la valeur limite d'une fonction ou d'une séquence fonctionnelle en un point, calculer ultime la valeur de la fonction à l'infini. déterminer la convergence d'une série de nombres et bien plus encore peut être fait grâce à notre service en ligne -. Nous vous permettons de trouver en ligne les limites de fonction de manière rapide et précise. Vous saisissez vous-même la variable de fonction et la limite vers laquelle elle tend, et notre service effectue pour vous tous les calculs, en donnant une réponse précise et simple. Et pour trouver la limite en ligne vous pouvez saisir à la fois des séries numériques et des fonctions analytiques contenant des constantes en expression littérale. Dans ce cas, la limite trouvée de la fonction contiendra ces constantes comme arguments constants dans l'expression. Notre service résout tous les problèmes complexes de recherche limites en ligne, il suffit d'indiquer la fonction et le point où il faut calculer valeur limite de la fonction. Calculateur limites en ligne, vous pouvez utiliser diverses méthodes et règles pour les résoudre, tout en vérifiant le résultat obtenu avec résoudre les limites en ligne sur le site www.site, ce qui mènera à la réussite de la tâche - vous éviterez vos propres erreurs et erreurs d'écriture. Ou vous pouvez nous faire entièrement confiance et utiliser notre résultat dans votre travail, sans consacrer d'efforts ni de temps supplémentaires au calcul indépendant de la limite de la fonction. Nous autorisons la saisie de valeurs limites telles que l'infini. Il est nécessaire de saisir un membre commun d'une séquence de numéros et www.site calculera la valeur limite en ligneà plus ou moins l'infini.

L'un des concepts de base de l'analyse mathématique est limite de fonction Et limite de séquence en un point et à l'infini, il est important de pouvoir résoudre correctement limites. Avec notre service, cela ne sera pas difficile. Une décision est prise limites en ligne en quelques secondes, la réponse est précise et complète. L'étude de l'analyse mathématique commence par passage à la limite, limites sont utilisés dans presque tous les domaines des mathématiques supérieures, il est donc utile d'avoir un serveur à portée de main pour solutions de limites en ligne, qui est matematikam.ru.

Lors du calcul des limites, il convient de prendre en compte les règles de base suivantes:

1. La limite de la somme (différence) des fonctions est égale à la somme (différence) des limites des termes :

2. La limite d'un produit de fonctions est égale au produit des limites des facteurs :

3. La limite du rapport de deux fonctions est égale au rapport des limites de ces fonctions :

.

4. Le facteur constant peut être pris au-delà du signe limite :

.

5. La limite d'une constante est égale à la constante elle-même :

6. Pour les fonctions continues, les symboles de limite et de fonction peuvent être intervertis :

.

Trouver la limite d'une fonction doit commencer par remplacer la valeur dans l'expression de la fonction. De plus, si la valeur numérique 0 ou ¥ est obtenue, alors la limite souhaitée a été trouvée.

Exemple 2.1. Calculez la limite.

Solution.

.

Les expressions de la forme , , , , , sont appelées incertitudes.

Si vous obtenez une incertitude de la forme , alors pour trouver la limite, vous devez transformer la fonction de manière à révéler cette incertitude.

L'incertitude de forme est généralement obtenue lorsque la limite du rapport de deux polynômes est donnée. Dans ce cas, pour calculer la limite, il est recommandé de factoriser les polynômes et de les réduire d'un facteur commun. Ce multiplicateur est nul à la valeur limite X .

Exemple 2.2. Calculez la limite.

Solution.

En remplaçant , nous obtenons l'incertitude :

.

Factorisons le numérateur et le dénominateur :

;

Réduisons d'un facteur commun et obtenons

.

Une incertitude de forme est obtenue lorsque la limite du rapport de deux polynômes est donnée à . Dans ce cas, pour le calculer, il est recommandé de diviser les deux polynômes par X au diplôme supérieur.

Exemple 2.3. Calculez la limite.

Solution. En substituant ∞, on obtient une incertitude de la forme , on divise donc tous les termes de l'expression par x3.

.

Il est pris en compte ici que .

Lors du calcul des limites d'une fonction contenant des racines, il est recommandé de multiplier et de diviser la fonction par son conjugué.

Exemple 2.4. Calculer la limite

Solution.

Lors du calcul des limites pour révéler une incertitude de la forme ou (1) ∞, les première et deuxième limites remarquables sont souvent utilisées :

De nombreux problèmes associés à la croissance continue d’une certaine quantité conduisent à la deuxième limite remarquable.

Considérons l'exemple de Ya. I. Perelman, donnant une interprétation du nombre e dans le problème des intérêts composés. Dans les caisses d’épargne, les intérêts sont ajoutés chaque année au capital fixe. Si l'adhésion est effectuée plus souvent, le capital croît plus rapidement, puisqu'un montant plus important est impliqué dans la formation des intérêts. Prenons un exemple purement théorique et très simplifié.

Que 100 deniers soient déposés à la banque. unités sur la base de 100 % par an. Si les intérêts ne sont ajoutés au capital fixe qu'après un an, alors à cette période, 100 deniers. unités se transformera en 200 unités monétaires.

Voyons maintenant ce que deviendront 100 denize. unités, si les intérêts sont ajoutés au capital fixe tous les six mois. Après six mois, 100 deniers. unités augmentera de 100 × 1,5 = 150, et après six mois supplémentaires - de 150 × 1,5 = 225 (den. unités). Si l'adhésion se fait tous les 1/3 de l'année, alors après un an 100 den. unités se transformera en 100 × (1 +1/3) 3 "237 (den. unités).

Nous augmenterons les conditions d'ajout d'intérêts à 0,1 an, à 0,01 an, à 0,001 an, etc. Puis sur 100 deniers. unités au bout d'un an ce sera :

100 × (1 +1/10) 10 » 259 (unités den.),

100 × (1+1/100) 100 » 270 (unités den.),

100 × (1+1/1000) 1000 » 271 (unités den.).

Avec une réduction illimitée des modalités d'ajout des intérêts, le capital accumulé ne croît pas indéfiniment, mais se rapproche d'une certaine limite égale à environ 271. Le capital déposé à 100 % par an ne peut augmenter de plus de 2,71 fois, même si les intérêts courus ont été ajoutés à la capitale toutes les secondes parce que

Exemple 2.5. Calculer la limite d'une fonction

Solution.

Exemple 2.6. Calculer la limite d'une fonction .

Solution. En substituant, nous obtenons l'incertitude :

.

A l'aide de la formule trigonométrique, on transforme le numérateur en produit :

En conséquence nous obtenons

Ici, la deuxième limite remarquable est prise en compte.

Exemple 2.7. Calculer la limite d'une fonction

Solution.

.

Pour révéler l'incertitude de la forme ou, vous pouvez utiliser la règle de L'Hôpital, qui repose sur le théorème suivant.

Théorème. La limite du rapport de deux fonctions infinitésimales ou infiniment grandes est égale à la limite du rapport de leurs dérivées

A noter que cette règle peut être appliquée plusieurs fois de suite.

Exemple 2.8. Trouver

Solution. Lors de la substitution, nous avons une incertitude sur la forme. En appliquant la règle de L'Hôpital, on obtient

Continuité de fonction

Une propriété importante d'une fonction est la continuité.

Définition. La fonction est considérée continu, si un petit changement dans la valeur de l'argument entraîne un petit changement dans la valeur de la fonction.

Mathématiquement, cela s'écrit comme suit : quand

Par et, on entend l'incrément des variables, c'est-à-dire la différence entre les valeurs suivantes et précédentes : , (Figure 2.3)

Figure 2.3 – Incrément des variables

De la définition d'une fonction continue au point, il s'ensuit que . Cette égalité signifie que trois conditions sont remplies :

Solution. Pour la fonction le point est suspect d'une discontinuité, vérifions cela et trouvons des limites unilatérales

Ainsi, , Moyens - point d'arrêt

Dérivée d'une fonction

Limite de fonction- nombre un sera la limite d'une quantité variable si, au cours de son changement, cette quantité variable se rapproche indéfiniment un.

Ou en d'autres termes, le nombre UN est la limite de la fonction y = f(x)à ce point x0, si pour toute séquence de points du domaine de définition de la fonction , différent x0, et qui converge vers le point x 0 (lim x n = x0), la séquence des valeurs de fonction correspondantes converge vers le nombre UN.

Le graphique d'une fonction dont la limite, étant donné un argument qui tend vers l'infini, est égale à L:

Signification UN est limite (valeur limite) de la fonction f(x)à ce point x0 dans le cas d'une séquence de points , qui converge vers x0, mais qui ne contient pas x0 comme l'un de ses éléments (c'est-à-dire dans le voisinage perforé x0), séquence de valeurs de fonction converge vers UN.

Limite d'une fonction de Cauchy.

Signification UN sera limite de la fonction f(x)à ce point x0 si pour tout nombre non négatif pris à l'avance ε le nombre non négatif correspondant sera trouvé δ = δ(ε) tel que pour chaque argument X, satisfaisant la condition 0 < | x - x0 | < δ , l'inégalité sera satisfaite | f(x)UNE |< ε .

Ce sera très simple si vous comprenez l'essence de la limite et les règles de base pour la trouver. Quelle est la limite de la fonction F (X)à X luttant pour unéquivaut à UN, s'écrit ainsi :

De plus, la valeur vers laquelle tend la variable X, peut être non seulement un nombre, mais aussi l'infini (∞), parfois +∞ ou -∞, ou il peut n'y avoir aucune limite.

Pour comprendre comment trouver les limites d'une fonction, il est préférable de regarder des exemples de solutions.

Il faut trouver les limites de la fonction F (x) = 1/Xà:

X→ 2, X→ 0, X→ ∞.

Trouvons une solution à la première limite. Pour ce faire, vous pouvez simplement remplacer X le nombre vers lequel il tend, c'est-à-dire 2, on obtient :

Trouvons la deuxième limite de la fonction. Ici, remplacez plutôt le 0 pur X c'est impossible, parce que Vous ne pouvez pas diviser par 0. Mais on peut prendre des valeurs proches de zéro, par exemple 0,01 ; 0,001 ; 0,0001 ; 0,00001 et ainsi de suite, et la valeur de la fonction F (X) augmentera : 100 ; 1000 ; 10 000 ; 100 000 et ainsi de suite. Ainsi, on peut comprendre que lorsque X→ 0 la valeur de la fonction qui est sous le signe limite augmentera sans limite, c'est-à-dire tendre vers l'infini. Ce qui signifie:

Concernant la troisième limite. La même situation que dans le cas précédent, il est impossible de substituer ∞ dans sa forme la plus pure. Il faut considérer le cas d'une augmentation illimitée X. Nous en substituons 1000 un par un ; 10 000 ; 100000 et ainsi de suite, on a ça la valeur de la fonction F (x) = 1/X diminuera : 0,001 ; 0,0001 ; 0,00001 ; et ainsi de suite, tendant vers zéro. C'est pourquoi:

Il faut calculer la limite de la fonction

En commençant à résoudre le deuxième exemple, nous constatons une incertitude. De là, nous trouvons le degré le plus élevé du numérateur et du dénominateur - c'est x3, on le retire des parenthèses au numérateur et au dénominateur puis on le réduit de :

Répondre

La première étape dans trouver cette limite, remplacez la valeur 1 à la place X, ce qui entraîne une incertitude. Pour le résoudre, factorisons le numérateur et faisons-le en utilisant la méthode de recherche des racines d'une équation quadratique x2 + 2x-3:

D = 2 2 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ x1 = -3 ;x2= 1.

Le numérateur sera donc :

Répondre

Il s'agit de la définition de sa valeur spécifique ou d'une certaine zone où tombe la fonction, qui est limitée par la limite.

Pour résoudre les limites, suivez les règles :

Ayant compris l'essence et l'essentiel règles pour résoudre la limite, vous obtiendrez une compréhension de base de la façon de les résoudre.

Notions de limites de séquences et de fonctions. Lorsqu'il faut trouver la limite d'une suite, elle s'écrit : lim xn=a. Dans une telle séquence de séquences, xn tend vers a et n tend vers l’infini. La séquence est généralement représentée sous forme de série, par exemple :
x1, x2, x3...,xm,...,xn... .
Les séquences sont divisées en séquences croissantes et décroissantes. Par exemple:
xn=n^2 - séquence croissante
yn=1/n - séquence
Ainsi, par exemple, la limite de la séquence xn=1/n^ :
limite 1/n^2=0

x→∞
Cette limite est égale à zéro, puisque n→∞, et la séquence 1/n^2 tend vers zéro.

Typiquement, une quantité variable x tend vers une limite finie a, et x se rapproche constamment de a, et la quantité a est constante. Cela s'écrit comme suit : limx =a, tandis que n peut aussi tendre vers zéro ou vers l'infini. Il existe une infinité de fonctions dont la limite tend vers l’infini. Dans d'autres cas, lorsque par exemple la fonction ralentit un train, il est possible que la limite tende vers zéro.
Les limites ont un certain nombre de propriétés. En règle générale, toute fonction n'a qu'une seule limite. C'est la propriété principale de la limite. Leurs autres propriétés sont listées ci-dessous :
* Le montant plafond est égal à la somme des plafonds :
lim(x+y)=lim x+lim y
* La limite du produit est égale au produit des limites :
lim(xy)=lim x*lim y
* La limite du quotient est égale au quotient des limites :
lim(x/y)=lim x/lim y
* Le facteur constant est pris en dehors du signe limite :
lim(Cx)=C lim x
Étant donné une fonction 1 /x dans laquelle x →∞, sa limite est nulle. Si x→0, la limite d'une telle fonction est ∞.
Il existe des exceptions à ces règles pour les fonctions trigonométriques. Puisque la fonction sin x tend toujours vers l’unité lorsqu’elle tend vers zéro, l’identité lui vaut :
lim péché x/x=1

Dans un certain nombre de problèmes, il existe des fonctions pour lesquelles une incertitude apparaît lors du calcul des limites - une situation dans laquelle la limite ne peut pas être calculée. La seule façon de sortir de cette situation est d'appliquer la règle de L'Hôpital. Il existe deux types d'incertitudes :
* incertitude de la forme 0/0
* incertitude de la forme ∞/∞
Par exemple, une limite de la forme suivante est donnée : lim f(x)/l(x), et f(x0)=l(x0)=0. Dans ce cas, une incertitude de la forme 0/0 apparaît. Pour résoudre un tel problème, les deux fonctions sont différenciées, après quoi la limite du résultat est trouvée. Pour les incertitudes de type 0/0, la limite est :
lim f(x)/l(x)=lim f"(x)/l"(x) (à x→0)
La même règle est également vraie pour les incertitudes de type ∞/∞. Mais dans ce cas l’égalité suivante est vraie : f(x)=l(x)=∞
Grâce à la règle de L'Hôpital, vous pouvez trouver les valeurs de toutes limites dans lesquelles apparaissent des incertitudes. Un préalable à

volume - aucune erreur lors de la recherche de dérivés. Ainsi, par exemple, la dérivée de la fonction (x^2)" est égale à 2x. De là, nous pouvons conclure que :
f"(x)=nx^(n-1)

Pour ceux qui veulent apprendre à trouver des limites, dans cet article nous vous en parlerons. Nous n’entrerons pas dans la théorie, les enseignants la donnent généralement lors de cours magistraux. La « théorie ennuyeuse » devrait donc être notée dans vos cahiers. Si ce n'est pas le cas, vous pouvez lire des manuels tirés de la bibliothèque de l'établissement d'enseignement ou d'autres ressources Internet.

Ainsi, le concept de limite est très important dans l’étude des mathématiques supérieures, en particulier lorsque vous rencontrez le calcul intégral et comprenez le lien entre limite et intégrale. Le matériel actuel examinera des exemples simples, ainsi que des moyens de les résoudre.

Exemples de solutions

Exemple 1

Calculer a) $ \lim_(x \to 0) \frac(1)(x) $; b)$ \lim_(x \to \infty) \frac(1)(x) $

Solution

a) $$ \lim \limits_(x \to 0) \frac(1)(x) = \infty $$ b)$$ \lim_(x \to \infty) \frac(1)(x) = 0 $$ Les gens nous envoient souvent ces limites en nous demandant d’aider à les résoudre. Nous avons décidé de les souligner à titre d'exemple distinct et d'expliquer que ces limites doivent simplement être rappelées, en règle générale. Si vous ne parvenez pas à résoudre votre problème, envoyez-le-nous. Nous fournirons une solution détaillée. Vous pourrez visualiser la progression du calcul et obtenir des informations. Cela vous aidera à obtenir votre note de votre professeur en temps opportun !

Répondre

$$ \text(a)) \lim \limits_(x \to 0) \frac(1)(x) = \infty \text( b))\lim \limits_(x \to \infty) \frac(1 )(x) = 0$$

Que faire de l'incertitude de la forme : $ \bigg [\frac(0)(0) \bigg ] $

Exemple 3

Résoudre $ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) $

Solution

Comme toujours, nous commençons par substituer la valeur $ x $ dans l'expression sous le signe limite. $$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = \frac((-1)^2-1)(-1+1)=\frac( 0)(0) $$ Quelle est la prochaine étape maintenant ? Que devrait-il se passer à la fin ? Puisqu’il s’agit d’une incertitude, ce n’est pas encore une réponse et nous continuons le calcul. Puisque nous avons un polynôme dans les numérateurs, nous allons le factoriser en utilisant la formule familière à tout le monde à l'école $$ a^2-b^2=(a-b)(a+b) $$. Vous souvenez-vous? Super! Maintenant, allez-y et utilisez-le avec la chanson :) On trouve que le numérateur $ x^2-1=(x-1)(x+1) $ Nous continuons à résoudre en tenant compte de la transformation ci-dessus : $$ \lim \limits_(x \to -1)\frac(x^2-1)(x+1) = \lim \limits_(x \to -1)\frac((x-1)(x+ 1 ))(x+1) = $$ $$ = \lim \limits_(x \to -1)(x-1)=-1-1=-2 $$

Répondre

$$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = -2 $$

Poussons la limite des deux derniers exemples à l'infini et considérons l'incertitude : $ \bigg [\frac(\infty)(\infty) \bigg ] $

Exemple 5

Calculer $ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) $

Solution

$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \frac(\infty)(\infty) $ Ce qu'il faut faire? Que dois-je faire? Pas de panique, car l'impossible est possible. Il faut retirer le x au numérateur et au dénominateur, puis le réduire. Après cela, essayez de calculer la limite. Essayons... $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) =\lim \limits_(x \to \infty) \frac(x^2(1-\frac (1)(x^2)))(x(1+\frac(1)(x))) = $$ $$ = \lim \limits_(x \to \infty) \frac(x(1-\frac(1)(x^2)))((1+\frac(1)(x))) = $$ En utilisant la définition de l'exemple 2 et en remplaçant x par l'infini, nous obtenons : $$ = \frac(\infty(1-\frac(1)(\infty)))((1+\frac(1)(\infty))) = \frac(\infty \cdot 1)(1+ 0) = \frac(\infty)(1) = \infty $$

Répondre

$$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \infty $$

Algorithme de calcul des limites

Alors, résumons brièvement les exemples et créons un algorithme pour résoudre les limites :

1. Remplacez le point x dans l'expression qui suit le signe limite. Si un certain nombre ou l’infini est obtenu, alors la limite est complètement résolue. Sinon, nous avons une incertitude : « zéro divisé par zéro » ou « l'infini divisé par l'infini » et passons aux étapes suivantes des instructions.
2. Pour éliminer l’incertitude de « zéro divisé par zéro », vous devez factoriser le numérateur et le dénominateur. Réduisez les similaires. Remplacez le point x dans l'expression sous le signe limite.
3. Si l’incertitude est « l’infini divisé par l’infini », alors nous supprimons au maximum le numérateur et le dénominateur x. Nous raccourcissons les X. Nous substituons les valeurs de x sous la limite dans l'expression restante.

Dans cet article, vous avez appris les bases de la résolution des limites, souvent utilisées dans le cours de calcul. Bien entendu, il ne s’agit pas de tous les types de problèmes proposés par les examinateurs, mais seulement des limites les plus simples. Nous parlerons d'autres types de missions dans de prochains articles, mais vous devez d'abord apprendre cette leçon pour pouvoir avancer. Discutons de ce qu'il faut faire s'il y a des racines, des degrés, étudions les fonctions équivalentes infinitésimales, les limites remarquables, la règle de L'Hôpital.

Si vous ne parvenez pas à déterminer vous-même les limites, ne paniquez pas. Nous sommes toujours heureux d'aider!