Matemātika dabā: piemēri. Matemātika dabā, numeroloģija dzīvē Harmonijas jēdziens

Harmonijas jēdziens. Matemātiskie kompozīcijas likumi

Kompozīcijas pamati lietišķajā grafikā

Jau senos laikos cilvēks atklāja, ka visas parādības dabā ir saistītas viena ar otru, ka viss atrodas nepārtrauktā kustībā, mainās un, izsakoties skaitļos, atklāj pārsteidzošus rakstus.

Klasiskā laikmeta senajā Grieķijā radās vairākas mācības par harmoniju. No tiem Pitagora mācība atstāja visdziļāko zīmi pasaules kultūrā. Pitagora sekotāji pasauli, Visumu, telpu, dabu un cilvēku iztēlojās kā vienotu veselumu, kur viss ir savstarpēji saistīts un harmoniskās attiecībās. Harmonija šeit darbojas kā kārtības sākums – haosa sakārtošana. Harmonija ir raksturīga dabai un mākslai: " Tie paši likumi pastāv mūzikas režīmiem un planētām". Pitagorieši un viņu sekotāji meklēja skaitlisku izteiksmi visam pasaulē. Viņi atklāja, ka mūzikas pamatā ir matemātiskas proporcijas (stīgas garuma attiecība pret augstumu, attiecība starp intervāliem, skaņu attiecība akordos kas rada harmonisku skaņu). cilvēka ķermeņa proporcijas un apstiprināja skaistuma matemātisko kanonu, saskaņā ar kuru tēlnieks Polikleitos izveidoja statuju “Kanons”.

Visai Grieķijas klasiskajai mākslai ir Pitagora proporciju doktrīnas zīmogs. Tās ietekmi piedzīvoja viduslaiku, renesanses, mūsdienu zinātnes un mākslas zinātnieki līdz pat mūsdienām. Pēc pitagoriešiem viduslaiku zinātnieks Augustīns skaistumu sauca par "skaitlisko vienlīdzību". Skolas filozofs Bonaventure rakstīja: "Nav skaistuma un baudas bez proporcionalitātes, un proporcionalitāte pastāv galvenokārt skaitļos. Ir nepieciešams, lai viss būtu saskaitāms." Leonardo da Vinči savā traktātā par glezniecību rakstīja par proporcijas izmantošanu mākslā: " Gleznotājs proporcijas veidā iemieso tos pašus dabā apslēptos modeļus, kurus zinātnieks zina skaitliskā likuma veidā".

Tādējādi proporcionalitāte, veseluma daļu proporcionalitāte ir vissvarīgākais veseluma harmonijas nosacījums un matemātiski izsakāms caur proporcijām.

Proporcija nozīmē divu vai vairāku attiecību vienādību. Ir vairāki proporcionalitātes veidi:

• matemātiskā,
• harmoniska,
• ģeometriski utt.

Matemātikā divu attiecību vienādību izsaka ar formulu a:b=с:d, un katru tā dalībnieku var definēt, izmantojot pārējos trīs. Ir 3 elementi harmoniskā proporcijā. Tās ir vai nu dažu elementu trīskāršu atšķirības pa pāriem, vai arī paši elementi, piemēram:

a:c=(a–c): (c–c)

Ģeometriskā proporcijā ir arī tikai 3 elementi, bet viens no tiem ir kopīgs, a:b=c:c. Ģeometriskās proporcijas veids ir tā sauktās " zelta griezums"kam ir tikai divi dalībnieki -" A" Un " V" ir iecienīta mākslinieku proporcija, ko Renesansē sauca par "dievišķo proporciju".

Zelta attiecība (g.s.)

Zelta griezuma proporcijas īpatnība ir tāda, ka pēdējais termins tajā ir starpība starp diviem iepriekšējiem terminiem, t.i.

a:b=c: (a–c)

• Attieksme h. Ar. izteikts kā skaitlis 0,618 .
• Proporcija z. Ar. 1:0,618=0,618:0,382 .

Ja izsakāt taisnas līnijas segmentu ar vienu un pēc tam sadalāt to divos segmentos ar z. s., tad lielākais segments būs vienāds ar 0,618, bet mazākais segments būs 0,382.

2. att. Segmenta dalījums pēc zelta griezuma

Pamatojoties uz proporciju h. Ar. tika izveidota skaitļu sērija, kas ir ievērojama ar to, ka katrs nākamais skaitlis izrādījās vienāds ar divu iepriekšējo skaitļu summu: 1, 1, 2, 3, 5, 8, 13, 21 utt. Šo sēriju atklāja itāļu matemātiķis Fibonači un tāpēc tiek saukts par Fibonači sēriju . Tam ir īpašība, ka attiecības starp blakus esošajiem terminiem, palielinoties rindu skaitļiem, arvien vairāk tuvojas O, b18, tas ir, attiecībai 3. Ar.

Proporcijas h. Ar. zinātnieki saista ar organisko vielu attīstību. h. Ar. Tas tika atklāts dzīvās dabas objektos - gliemežvāku uzbūvē, kokā, saulespuķu sēklu izvietojumā, cilvēka ķermeņa uzbūvē, un tas tika novērots arī Visuma uzbūvē planētu izvietojumā.

Attiecībā uz s. Ar. Ir arī ģeometrisku formu elementi - piecstūris, zvaigzne.

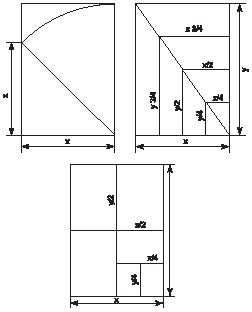
Taisnstūrī h. Ar. puses ir saistībā ar z.s. Šajā taisnstūrī ir kvadrāts un mazs taisnstūris h. Ar. (tā lielā mala ir sākotnējā taisnstūra mazā mala.) Tāpēc ir iespējams konstruēt pr-k z.s. pamatojoties uz kvadrātu: kvadrāta malu sadala uz pusēm, no tā punkta uz augšu novelk diagonāli, ar kuras palīdzību kvadrāta malā izbūvē pr-k z.s.

Līniju, kas veido zvaigzni, krustošanās punkti sadala tos segmentos attiecībā pret zelta griezumu. Šis mazais taisnstūris ir līdzīgs lielam taisnstūrim, kas sastāv no kvadrāta un maza taisnstūra h. s., tas ir, abi šie taisnstūri ir taisnstūri h. Ar.

Citiem vārdiem sakot, ja jūs nogriežat z no taisnstūra. c.. kvadrāts, tad paliek mazāks taisnstūris, kura malas atkal būs attiecībā z. Ar. Sadalot šo mazāko taisnstūri kvadrātā un vēl mazākā taisnstūrī, mēs atkal iegūstam taisnstūri 3. s. un tā tālāk bezgalīgi. Ja savienosim līknes kvadrātu virsotnes, iegūsim logaritmisku līkni, bezgalīgi augošu spirāli, ko sauc par “attīstības līkni”, “dzīvības spirāli”, jo šķiet, ka tā satur ideju par bezgalīga attīstība.

Rīsi. 4. Taisnstūris aptuveni zelta griezumā, kas veidots uz piecstūra pamata

5. att. Zelta griezuma taisnstūra uzbūve, pamatojoties uz kvadrātu.

Bezgalīga atkārtošanās h. Ar. un kvadrāts, sadalot taisnstūri h. Ar. atklāj veseluma atkārtošanos tā daļās, kas ir viens no veseluma harmonijas nosacījumiem. Tā ir taisnstūra īpašība g.s. atklāja mākslinieki un viņi sāka izmantot s. Ar. kā saskaņošanas, samērošanas veids. Phidias izmantoja z. Ar. Akropoles celtniecības laikā (5. gadsimtā pirms mūsu ēras)

Rīsi. 6. Logaritmiskā līkne "Dzīvības spirāle"

Rīsi. 7. Vēstules konstrukcija no Luka Pačioli grāmatas “Par dievišķo proporciju”

Arī grieķu amatnieki, veidojot keramiku, izmantoja sēru. Ar. Renesanses laikā h. Ar. izmanto ne tikai arhitektūrā, tēlniecībā, glezniecībā, bet arī dzejā un mūzikā. Dīrers, Leonardo da Vinči un viņa skolnieks Luka Pacioli izmantoja s. Ar. harmonisku burtu proporciju meklējumos. Taisnstūris h. Ar. atrodam gan viduslaiku rokraksta grāmatu proporcijās, gan mūsdienu grāmatās, jo slaidās proporcijas h. Ar. ļauj skaisti sakārtot grāmatas lappuses vietu un izplatīties.

Rīsi. 8. Viduslaiku rokraksta ideālo proporciju shēma.

Lapas proporcijas ir 2:3, un plakne, ko aizņem burts, ir zelta griezuma proporcijā.

Rīsi. 9. Viens no veidiem, kā noteikt drukas joslas izmēru dotajam formātam.

Proporcija ir veseluma daļu apvienošana vienā proporcionālā struktūrā.

Divdesmitajā gadsimtā atkal parādījās interese par zelta griezumu kā proporcionalitātes metodi.

Tas piesaistīja arhitektu uzmanību. Padomju arhitekts Žoltovskis un francūzis Korbizjē nodarbojās ar sanitārijas problēmām. Ar. un izmantoja to savā arhitektūras praksē, Korbizjē izveidoja veselu proporciju sistēmu, pamatojoties uz zelta griezuma sērijas skaitļiem un cilvēka ķermeņa proporcijām, un nosauca to par "Modulor", kas latīņu valodā nozīmē "ritmiski mērīt".

Rīsi. 9. Modulors (vienkāršota diagramma)

Rīsi. 10. Taisnstūra sadalīšanas iespējas, pamatojoties uz Modulor.

Korbizjē modulis attēlo harmoniskas skaitļu sērijas, kas ir savienotas vienotā sistēmā un ir paredzētas izmantošanai arhitektūrā un dizainā – lai harmonizētu visu vidi, kurā cilvēks dzīvo. Korbizjē sapņoja par visas arhitektūras un objektu vides pārstrukturēšanu ar Modulor palīdzību. Viņš pats radīja vairākus izcilus arhitektūras piemērus, taču plašāks Modulor pielietojums esošajos apstākļos nebija ne runas.

Modulor ir izmantots vairākos veidos dizainā un grafiskajā dizainā - drukāto izdevumu dizainā. Attēlā 16. attēlā ir parādītas 3:4 taisnstūra sadalīšanas iespējas, ko sniedzis Korbizjē, lai demonstrētu dizaina iespējas, izmantojot Modulor.

D. Hambidžs sniedza savu ieguldījumu jautājuma izstrādē par proporcijas un zelta griezuma izmantošanu. 1920. gadā Ņujorkā tika izdota viņa grāmata “Dinamiskās simetrijas elementi”. Hambidžs pētīja dinamisko simetriju, ko viņš atklāja taisnstūru sērijā, lai mākslinieki to praktiski pielietotu kompozīcijas veidošanā. Viņš mēģina atklāt noslēpumus, ko senie grieķi izmantoja, lai panāktu harmonisku formas risinājumu. Viņa uzmanību piesaistīja taisnstūru īpašības, kas veido rindu, kur katrs nākamais taisnstūris ir veidots uz iepriekšējā diagonāles, sākot ar kvadrāta C2 diagonāli. Tie ir taisnstūri C4, C5 (kuru mazākā mala ir vienāda ar kvadrāta malu, ņemot par vienu). (17. att.). Sērijas kulminācija ir taisnstūris T5, kuram ir īpašas harmoniskās īpašības un kas ir “saistīts” ar zelta griezuma taisnstūri (par to tiks runāts tālāk).

Rīsi. 11. Dinamisku Hembidža taisnstūru sērija.

Hambidžs ņem vērā arī šo taisnstūru malās uzcelto kvadrātu laukumus un atklāj šādu dinamiku: uzdevumā C2 kvadrātam, kas uzbūvēts no lielākās malas, ir 2 reizes lielāks laukums nekā kvadrātam, kas uzbūvēts mazākajā pusē. Vingrojumā C3 kvadrāts no lielākās malas ir 3 reizes lielāks nekā kvadrāts mazākajā malā utt. Tādā veidā tiek veidotas dinamiskas apgabalu sērijas, kas sastāv no veseliem skaitļiem.

Hambidžs apgalvo, ka senie grieķi izmantoja šo principu savos kompozīcijas lēmumos. Laikrindu taisnstūri, par kuriem mēs runājām, ir primārie apgabali Hambidžas kompozīcijas sistēmā. Katru no šiem taisnstūriem var sadalīt atsevišķās daļās un radīt jaunus kompozīcijas risinājumus un jaunas tēmas. Piemēram, taisnstūri C5 var sadalīt kvadrātā un divos zelta griezuma taisnstūros. Zelta griezuma taisnstūri var sadalīt kvadrātā un zelta griezuma taisnstūrī, kā arī var sadalīt vienādās daļās, un tiek atklāts šāds modelis: sadalot uz pusēm, tas iegūs divus taisnstūrus, no kuriem katrā būs divi zeltaini. attiecību taisnstūri. Sadalot trīs daļās, katrā trešdaļā ir trīs zelta griezuma taisnstūri. Sadalot 4 daļās - četri taisnstūri h. Ar. katrā galvenā taisnstūra ceturtdaļā.

Starp arhitektūrā, dizainā un lietišķajā grafikā izmantotajām proporciju sistēmām jāmin “vēlamo skaitļu” sistēmas un dažādas moduļu sistēmas.

"Vēlamie numuri" - ģeometriskās progresijas skaitļu virkne, kur katrs nākamais skaitlis tiek veidots, reizinot iepriekšējo skaitli ar kādu nemainīgu vērtību. Iepakojuma noformējumā, reklāmas plakātu kompozīcijā tiek izmantoti skaitļi no vēlamās sērijas. Tie nodrošina formas ritmiskā attīstība, tās atrodamas arī seno formu vāzu konstrukcijā un modernā mašīnā.

Labi pazīstama proporciju sistēma ir tā sauktā " Itāļu ierindas", kuru pamatā ir pirmie Fibonači sērijas skaitļi - 2, 3, 5. Katrs no šiem skaitļiem, dubultojot, veido skaitļu virkni, kas harmoniski saistīti viens ar otru:

• 2 - 4, 8, 16, 32, 64 utt.
• 3 - 6, 12, 24 48, 96
• 5 - 10, 20, 40, 80, 160

Proporcija ir saistīta ar jēdzieniem proporcionalitāte Un pasākumiem. Viens no veidiem, kā izmērīt veselumu un tā daļas, ir modulis. Modulis- izmērs vai elements, kas atkārtoti atkārtojas kopumā un tā daļās. Modulis(Latīņu) nozīmē mērs. Jebkurš garuma mērs var būt modulis. Grieķu tempļu būvniecības laikā tika izmantots arī modulis, lai panāktu proporcionalitāti. Modulis varētu būt kolonnas rādiuss vai diametrs, attālums starp kolonnām.

Vitruvijs, 1. gadsimta romiešu arhitekts. BC e., savā traktātā par arhitektūru viņš rakstīja, ka proporcija ir atbilstība starp visa darba dalībniekiem un tā veselumu - attiecībā pret daļu, kas tiek uzskatīta par oriģinālu, uz kuru balstās visa proporcionalitāte, un proporcionalitāte ir stingra harmonija. pašas konstrukcijas atsevišķām daļām un atsevišķu daļu atbilstība un vienas konkrētas daļas veselums, kas tiek uzskatīts par sākotnējo.

Lietišķajā grafikā modulis tiek plaši izmantots grāmatu, žurnālu, laikrakstu, katalogu, prospektu un visu veidu drukāto publikāciju noformēšanā. Moduļu režģu izmantošana palīdz sakārtot tekstu un ilustrāciju izkārtojumu un veicina kompozīcijas vienotības radīšanu. Drukāto publikāciju modulārais dizains ir balstīts uz vertikālu un horizontālu līniju kombināciju, kas veido režģi, sadalot lapu (lapu) taisnstūros, kas paredzēti teksta, ilustrāciju un atstarpes izplatīšanai starp tām. Šis taisnstūra modulis (tie var būt vairāki) nosaka ritmiski sakārtotu materiāla sadalījumu drukātajā izdevumā.

Ir dažādu modeļu un sarežģītības pakāpes režģi. A. Hurlberts grāmatā “Režģis” sniedz žurnālu, grāmatu un laikrakstu moduļu režģu piemērus.

Moduļu režģi nedrīkst jaukt ar tipogrāfisko režģi, kas nosaka lauku izmērus un salikšanas lapas formātu. Protams, modulārajā režģī, ciktāl tas attiecas uz drukātajām publikācijām, ir jāņem vērā līniju izmēri, burtu augstums un atstarpju elementi tipogrāfiskajos mēros (kvadrāti, ciceros, punkti), lai pareizi novietotu drukāto materiālu. lapā.

Režģa sistēma, pateicoties tās skaidram modulārajam pamatam, ļauj publikāciju izstrādes procesā ieviest elektroniskās programmas. Lietišķajā, rūpnieciskajā grafikā moduļu režģis tiek izmantots visu veidu reklāmas publikāciju noformēšanā un jo īpaši grafiskā korporatīvā stila dizainā. Moduļu režģis tiek izmantots dažādu zīmju, vizuālo komunikāciju zīmju, preču zīmju u.c.

Rīsi. 14. Preču zīme, kas veidota uz moduļu režģa bāzes.

Rīsi. 15. Sakaru zīme Olimpiskajām spēlēm Minhenē. veidota uz modulāra režģa

Moduļu režģu pamatā bieži ir kvadrāts. Kvadrāts ir ļoti ērts modulis. To plaši izmanto kā moduli mūsdienu mēbeļu rūpniecībā, jo īpaši saliekamo mēbeļu, “sienu” konstrukcijā.

Dubultais laukums jau izsenis pazīstams kā tradicionālās japāņu mājas modulis, kurā telpu izmēri bija atbilstoši tam, cik reižu uz grīdas tiks klāts tatami paklājiņš ar dubultā kvadrāta proporcijām.

Lietišķajā grafikā kvadrāts tiek izmantots albumu prospektu un bērnu grāmatu formātiem, taču tas nosaka arī šo izdevumu iekšējo telpu. Kvadrātveida moduli var izmantot arī formātā, kas nav kvadrātveida.

Dosim piemēru kvadrātveida moduļa izmantošanai kvadrātveida formātā: ar trīs kolonnu teksta ievadīšanu visa tekstam un ilustrācijām atvēlētā platība tiek sadalīta 9 kvadrātos. Ja kolonnas platums ir norādīts kā 1, tad kvadrāts būs 1x1. Šajā gadījumā ilustrācijas var aizņemt apgabalus: 1x1, 1x2, 1x3, 2x2, 2x3, 3x3, 2x1 utt., tas ir, mums būs diezgan plašas iespējas apvienot ilustrācijas un tekstu izkārtojumā. Mākslas un dizaina darbu kompozīcijas struktūrā svarīgas ir taisnstūru un citu ģeometrisku formu proporcijas, kurās iederas dotais darbs vai tā galvenās daļas. Tāpēc mums vajadzētu apsvērt taisnstūrus, kurus visplašāk izmanto to harmonisko īpašību dēļ (zelta griezuma taisnstūris tika apspriests iepriekš). Paskatīsimies vēlreiz uz laukumu. Laukums kā strukturāla forma ir pazīstama jau sen. Viņš piesaistīja antīkās pasaules un renesanses mākslinieku uzmanību.

Leonardo da Vinči zīmējumā attēlota kvadrāta un apļa saikne ar senajiem cilvēkiem zināmo cilvēka figūru (Vitruvius). Renesanses mākslinieki - vācietis Durers, itālis Pacioli, francūzis Torijs, veidojot burtu kontūru, vadījās no kvadrāta formas, burts ar visiem tā elementiem iederas kvadrātā (12. att.), lai gan ne visi burti tika pielīdzināti kvadrātam, tomēr kopējā kompozīcijas struktūra tika noteikta kvadrātā. Kvadrāts ir stabila, statiska figūra. Tas asociējas ar kaut ko nekustīgu, pilnīgu. Senajā pasaulē dažu tautu vidū kvadrāta attēls bija saistīts ar nāves simboliku. (Šajā sakarā ir interesanti atzīmēt, ka kvadrātveida proporcijas dabā ir sastopamas nedzīvās matērijas formās, kristālos). Statiskā pabeigtības dēļ kvadrāts tiek izmantots lietišķajā grafikā, vizuālo komunikāciju jomā kopā ar apļa formu, kā elements, kas piesaista uzmanību, kā arī lai ierobežotu telpu, kurā tiek koncentrēta informācija.

Papildus zelta griezuma taisnstūrim un kvadrātam mūs visvairāk interesē taisnstūri Ts2 un Ts5. Klasiskā laikmeta senie grieķi deva priekšroku šiem taisnstūriem, apgalvo, ka 85% grieķu klasiskās mākslas darbu tika uzcelti uz C5 laukuma. Kas ir interesants šajā taisnstūrī? Sadalot vertikāli un horizontāli divās daļās, tas atjauno proporcijas. Šo taisnstūri var sadalīt kvadrātā un divos mazos zelta griezuma taisnstūros. Turklāt tas parāda divus zelta griezuma taisnstūrus, kas pārklājas viens ar otru kvadrāta lielumā. Atlikusī daļa ir arī zelta griezuma taisnstūris. Tādējādi taisnstūrim C5 piemīt ritmiskas īpašības. Tajā parādās skaista simetrija (mazs taisnstūris g.s. + kvadrāts + mazs taisnstūris g.s.).

Rīsi. 16. Taisnstūra ritmiskās īpašības

Hambidžs sniedz Bostonas muzeja grieķu dzeramā krūzes kompozīcijas diagrammu: krūze iekļaujas (bez rokturiem) horizontāli iegarenā taisnstūrī C5. Divu zelta griezuma taisnstūri, kas pārklājas kvadrātā, krustojas punktā, caur kuru. robeža starp kausu un tās pēdu iet garām. Kājas pamatnes platums ir vienāds ar bļodas augstumu un vienāds ar kvadrāta malu, kas atrodas taisnstūra C5 centrā. Kāja iekļaujas divos mazos taisnstūros h. s., kas nogriezts no kvadrāta ar līniju, kas ir horizontāla līdz avēnijas Ts5 pamatnei un iet cauri lielo taisnstūru h divu diagonāļu krustpunktam. Ar. Mūsdienu mākslinieciskajā dizainā plaši tiek izmantots arī Ts5 taisnstūris. Mēs to atrodam automašīnu, darbgaldu un citu produktu proporcijās. Lietišķajā grafikā - prospektu, bukletu, iepakojuma formātos; tēlotājmākslā, monumentālajā mākslā, attēla plaknes proporcijās, attēla kompozicionālajā struktūrā.

Arī Ts2 taisnstūris tiek plaši izmantots, īpaši lietišķās grafikas jomā. To izmanto kā papīra formātu biznesa dokumentiem, jo ​​tam piemīt pārsteidzoša īpašība – sadalot uz pusēm, tas nemaina savas proporcijas. Sadalot, veidojas vairāki līdzīgi taisnstūri, kurus harmoniski savieno formas vienotība. Attēlā 18. attēlā redzams taisnstūru attēls, ko izmanto kompozīcijas konstruēšanā, pateicoties to malu harmoniskajām attiecībām.

Rīsi. 17. Sānu proporcijas pr-ke Ts2, izmantots Poratmana standartā.

Rīsi. 18. Malu harmoniskās attiecības taisnstūros.

Zemāk ir norādītas pr-kov Ts2, Ts3, Ts4, Ts5 skaitliskās attiecības pret to savstarpējiem skaitļiem, ar kuriem tie ir harmoniskā attiecībā. (Cipara apgrieztā vērtība ir skaitlis, ko iegūst, dalot vienu ar noteiktu skaitli.) Ja ņemam taisnstūra mazāko malu par vienu, tad taisnstūrim skaitlis (atbilst taisnstūra lielākajai malai) = 1,4142, un apgrieztais skaitlis = 0,7071; pr-ka Ts3 skaitlim = 1,732, apgrieztais skaitlis = 0,5773; pr-ka Ts4 skaitlim = 2, apgrieztais skaitlis = 0,5; pr-ka Ts5 skaitlim = 2,236; abpusēja = 0,4472; pr-ka" z.s. skaitlis = 1,618, apgrieztais skaitlis = 0,618.

Pamatojoties uz Ts2 projektu, tika veikta grāmatu, papīru, biznesa dokumentu, pastkaršu, plakātu, mapju un citu ar lietišķo grafiku saistītu objektu formātu standartizācija un unifikācija. Šis standarts, kas pazīstams kā Dr. Porstmann standarts, ir pieņemts 17 Eiropas valstīs. Standarta pamatā bija formāts 841X1189 mm un laukums 1 m 2. Pārējie formāti, kas veido tās daļas, ir iegūti no tā:

• 1 m 2 - 841 x 1189 mm
• 1/2m 2 - 594 Х841 mm
• 1/4m 2 - 420 X 594 mm
• 1/8 m 2 - 297 × 420 mm (dubultā loksne)
• 1/16m 2 - 210Х 297mm (lapa biznesa sarakstei, veidlapas)
• 1/32m 2 - 148Х210mm (puslapas lietišķajai korespondencei, veidlapas)
• 1/64m 2 - 105X148mm (pastkarte)
• 1/128m 2 - 74Х105mm (vizītkarte)

Standarts paredz arī papildu formātus 1000X1414 un 917X1297 un to koplietojumus. Aploksnēm tiek piedāvāti šādi izmēri: 162X229 un 114X162. (Standarts nav norādīts pilnībā).

Rīsi. 19. Taisnstūra sadalīšana daļās: 1/2, 1/4, 1/8, 1/16,1/64.

Tā kā, rīkojoties ar biznesa papīriem un dokumentāciju, ir nepieciešams ne tikai pēc izmēra un formāta tām atbilstošas ​​aploksnes un mapes, bet arī konteineri, kuros tiek glabāta dokumentācija, līdz ar to ir nepieciešamas atbilstošas ​​mēbeles: galdi, skapji, plaukti. Mēbeļu izmēri un proporcijas savukārt liecina par telpu interjeru raksturu. Tādējādi rodas pilnīga saskaņotu interjera elementu sistēma, kas pakārtota vienam moduļu principam.

Proporcionālām attiecībām jāpastāv ne tikai starp atsevišķām veseluma daļām, bet arī starp objektiem, kas veido objektu grupas, ko savieno viens stils un funkcionāls uzdevums. Piemēram, starp objektiem, kas iekļauti korporatīvās identitātes sistēmā.

Cilvēku apņemošie objekti ir jāsaskaņo ne tikai vienam pret otru, bet arī jāsaista ar cilvēku ar vienu mērauklu, ar viņa fizisko struktūru. Senatnes arhitekti uzskatīja, ka arhitektūras daļu attiecībām viena ar otru un ar veselumu jāatbilst cilvēka ķermeņa daļām un to attiecībām. Tādā pašā veidā Korbizjē modulis izriet no cilvēka ķermeņa izmēriem un zelta griezuma attiecībām tajā (attālums no zemes līdz saules pinumam un attālums no saules pinuma līdz vainagam veido galējo un vidējo. zelta griezuma attiecības...

Liela mēroga attiecības starp lietām, objekta vidi un cilvēku darbojas kā harmonizācijas līdzeklis, jo mērogs ir viena no proporcionalitātes izpausmēm, kas nosaka relatīvas dimensijas starp cilvēku un objektu - arhitektūrā, dizainā, lietišķajā mākslā, jo īpaši lietišķajā grafikā, grāmatu mākslā. Tādējādi plakātu un visu vizuālās komunikācijas mērķiem kalpojošo objektu - zīmju, ceļa zīmju u.c. izmēri un formāti, kā arī to kompozīcijas risinājums vienmēr tiek izvēlēti atkarībā no mērķa un ekspluatācijas apstākļiem, tātad atbilstošās mēroga attiecībās. . Tas pats attiecas uz grāmatu dizaina jomu un visa veida drukāto reklāmu un iepakojumu.

Simetrija.

Proporcionāli un proporcionāli izpaužas kvantitatīvās attiecības starp veseluma daļām un veselumu. Grieķi tiem pievienoja arī simetriju, uzskatot to par proporcionalitātes veidu - kā tās īpašo gadījumu - identitāti. Tā, tāpat kā proporcija, tika uzskatīta par nepieciešamu nosacījumu harmonijai un skaistumam.

Simetrijas pamatā ir līdzība. Tas nozīmē tādas attiecības starp elementiem un figūrām, kad tās atkārtojas un līdzsvaro viena otru. Matemātikā simetrija nozīmē figūras daļu izlīdzināšanu, pārvietojot to attiecībā pret asi vai simetrijas centru.

Ir dažādi simetrijas veidi. Vienkāršākais simetrijas veids ir spogulis (aksiāls), kas rodas, kad figūra griežas ap simetrijas asi. Simetriju, kas rodas, kad figūra griežas ap rotācijas centru, sauc par centrālo. Bumbiņai ir visaugstākā simetrijas pakāpe, jo tās centrā krustojas bezgalīgs skaits asu un simetrijas plakņu. Absolūta, stingra simetrija ir raksturīga nedzīvajai dabai - kristāliem (minerāliem, sniegpārslām).

Organiskajai dabai un dzīvajiem organismiem ir raksturīga nepilnīga simetrija (kvazisimetrija) (piemēram, cilvēka uzbūvē). Simetrijas pārkāpums, asimetrija (simetrijas trūkums) tiek izmantota mākslā kā māksliniecisks līdzeklis. Neliela novirze no pareizas simetrijas, tas ir, kaut kāda asimetrija, izjaucot līdzsvaru, piesaista uzmanību, ievieš kustības elementu un rada dzīvas formas iespaidu. Dažādiem simetrijas veidiem ir atšķirīga ietekme uz estētisko izjūtu:

• spoguļa simetrija - līdzsvars, miers;
• spirālveida simetrija izraisa kustības sajūtu...

Khzmbidj visas vienkāršās ģeometriskās figūras klasificē kā statisko simetriju (visus simetrijas veidus sadalot statiskajā un dinamiskajā), un spirāli iekļauj kā dinamisko simetriju. Statiskās simetrijas pamatā bieži ir piecstūris (ziedu vai augļa griezums) vai kvadrāts (minerāļos). Mākslā stingru matemātisku simetriju izmanto reti.

Rīsi. 20. Simetrijas veidi: Spogulis, spirālveida, centrālais, bīdes.

Rīsi. 21. Hogarta "Grēcijas un skaistuma līnija".

Simetrija ir saistīta ar vidus un veseluma jēdzienu. Sengrieķu filozofijā un mākslā jēdziens “vidus, centrs” ir saistīts ar ideju par esamības integritāti. Vidējais - “izvairīšanās no galējībām” (Aristotelis) nozīmē līdzsvara principu. "Visur grieķis redzēja kaut ko veselu, un tas nozīmē, ka viņš vispirms fiksēja novērotā vai svešā objekta centru... Bez jēdziena "vidējais" nav iedomājama senā mācība par proporcijām, mēru, simetriju vai harmoniju.

Harmonija

Harmonija ir dialektisks jēdziens. Saskaņā ar sengrieķu mitoloģiju Harmonija ir kara dieva Āresa un mīlestības un skaistuma dievietes Afrodītes meita, proti, viņā ir sapludināti pretēji, karojoši principi. Tāpēc harmonijas jēdziens ietver kontrastu kā nepieciešamu nosacījumu. Kontrasts veicina dažādību un dažādību, bez kuras harmonija nav iedomājama.

"Harmonija ir daudzu vienotība un to, kas nepiekrīt, vienošanās"(Philolaus). Senie cilvēki to zināja. 18. gadsimta mākslinieks Hogārts atklāja, ka harmonijas būtība ir vienotībā un daudzveidībā. Viņš pielūdza viļņoto līniju, ko viņš uzskatīja " skaistuma un žēlastības līnija", jo tas ir konkrēts vienotības un daudzveidības iemiesojums. Bez daudzveidības skaistums nav iespējams. Monotonija nogurdina. Pretēja maiņā izpaužas dialektisks modelis - negācijas noliegums. Redzamajos mākslas tēlos tas ir kas izteikts ar ritmu un kontrastu, harmonijas jēga ir ierobežot haosu.

Bet viņa to dara, cīnoties ar pretējiem principiem. Apvienojot pretējus principus, harmonija tos līdzsvaro, ievieš mēru un vienošanos, sakārto un saņem skaistumu kā balvu.

Simetrija, proporcijas, ritms, kontrasts, integritāte – tie, kas veido harmoniju, ir objektīvi saistīti ar dabu, ar matērijas kustību un attīstību. Mūsu estētiskās idejas ir cieši saistītas ar šiem jēdzieniem. Taču cilvēka sociālā eksistence dažādos laikmetos skatījās uz harmonijas kategorijām no dažādiem leņķiem, un tas noteica to lomu sabiedriskajā dzīvē un mākslā. Ideja par skaistumu attīstījās un mainījās. Harmoniju sāka skatīt nevis kā kvantitatīvu, bet gan kā kvalitatīvu principu, kas apvieno fizisko un garīgo principu.

Ja senie grieķi par skaistu uzskatīja tikai sakārtotu skaistumu un uzskatīja par neglītu jebkuru simetrijas un proporciju pārkāpumu, tad turpmākajos laikmetos skaistuma izpausmes sāka atrasties kārtības pārkāpumos, disonancē, šķietamā disharmonijā, jo tās ir raksturīgas dzīvei. un tāpēc ir daļa no kādas citas harmoniskas sistēmas, kurā tie atrod loģiku un nozīmi. "Dzīve ir skaista," rakstīja Černiševskis. Un viņa nestāv uz vietas. Harmonijas izskats dabā un dzīvē ir plašāks par jebkuru kanonu, ko var aptvert jebkura harmoniskā sistēma. Un cilvēce nekad nebeigs meklēt jaunas harmoniskas attiecības, kombinācijas un meklēt citu hermonisku rakstu izpausmes. Tomēr tas nenozīmē, ka klasiskā harmonija ir zaudējusi savu nozīmi. Tas, kas jau ir atklāts, atrastie modeļi, to matemātiskais pamatojums, paliek mūžīgais cilvēces mantojums, no kura smelsies visas nākamās paaudzes.

• pāriet uz nākamo daļu - " "

Ja uzmanīgi paskatās apkārt, matemātikas loma cilvēka dzīvē kļūst acīmredzama. Datori, moderni telefoni un cita tehnika mūs pavada katru dienu, un to izveide nav iespējama bez lielās zinātnes likumu un aprēķinu izmantošanas. Tomēr matemātikas loma sabiedrībā neaprobežojas tikai ar šādiem lietojumiem. Citādi, piemēram, daudzi mākslinieki ar tīru sirdsapziņu varētu teikt, ka skolā uzdevumu risināšanai un teorēmu pierādīšanai veltītais laiks ir bijis velti. Tomēr tas tā nav. Mēģināsim izdomāt, kāpēc ir vajadzīga matemātika.

Bāze

Pirmkārt, ir vērts saprast, kas patiesībā ir matemātika. Tulkojumā no sengrieķu valodas pats nosaukums nozīmē “zinātne”, “mācība”. Matemātikas pamatā ir objektu formu skaitīšanas, mērīšanas un aprakstīšanas operācijas. uz kuriem balstās zināšanas par struktūru, kārtību un attiecībām. Tie ir zinātnes būtība. Reālu objektu īpašības tajā tiek idealizētas un uzrakstītas formālā valodā. Tādā veidā tie tiek pārvērsti matemātiskos objektos. Dažas idealizētas īpašības kļūst par aksiomām (apgalvojumiem, kuriem nav nepieciešami pierādījumi). Pēc tam tiek iegūtas citas patiesās īpašības. Tā veidojas reāls esošs objekts.

Divas sadaļas

Matemātiku var iedalīt divās papildinošās daļās. Teorētiskā zinātne nodarbojas ar iekšējo matemātisko struktūru dziļu analīzi. Lietišķā zinātne nodrošina savus modeļus citām disciplīnām. Fizika, ķīmija un astronomija, inženiertehniskās sistēmas, prognozēšana un loģika pastāvīgi izmanto matemātisko aparātu. Ar tās palīdzību tiek veikti atklājumi, tiek atklāti modeļi un prognozēti notikumi. Šajā ziņā matemātikas nozīmi cilvēka dzīvē nevar pārvērtēt.

Profesionālās darbības pamati

Bez matemātikas pamatlikumu zināšanām un prasmes tos izmantot mūsdienu pasaulē kļūst ļoti grūti apgūt gandrīz jebkuru profesiju. Ar skaitļiem un operācijām ar tiem nodarbojas ne tikai finansisti un grāmatveži. Bez šādām zināšanām astronoms nevarēs noteikt attālumu līdz zvaigznei un labāko laiku tās novērošanai, un molekulārbiologs nevarēs saprast, kā rīkoties ar gēnu mutāciju. Inženieris neprojektēs strādājošu signalizāciju vai videonovērošanas sistēmu, un programmētājs neatradīs pieeju operētājsistēmai. Daudzas no šīm un citām profesijām bez matemātikas vienkārši nepastāv.

Humanitārās zinātnes

Taču matemātikas loma cilvēka dzīvē, piemēram, nodevusies glezniecībai vai literatūrai, nav tik acīmredzama. Un tomēr zinātņu karalienes pēdas ir sastopamas arī humanitārajās zinātnēs.

Šķiet, ka dzeja ir tīra romantika un iedvesma, nav vietas analīzei un aprēķiniem. Tomēr pietiek atcerēties amfibrahu poētiskās dimensijas), un rodas sapratne, ka arī matemātikai šajā ziņā ir bijusi sava roka. Ritms, verbālais vai muzikālais, arī tiek aprakstīts un aprēķināts, izmantojot šīs zinātnes zināšanas.

Rakstniekam vai psihologam bieži ir svarīgi tādi jēdzieni kā informācijas ticamība, atsevišķs incidents, vispārinājums utt. Visi no tiem ir vai nu tieši matemātiski, vai arī ir veidoti, pamatojoties uz zinātņu karalienes izstrādātajiem likumiem, un pastāv, pateicoties viņai un saskaņā ar viņas noteikumiem.

Psiholoģija radās humanitāro un dabas zinātņu krustpunktā. Visi tā virzieni, pat tie, kas darbojas tikai ar attēliem, paļaujas uz novērošanu, datu analīzi, to vispārināšanu un pārbaudi. Šeit tiek izmantotas modelēšanas, prognozēšanas un statistikas metodes.

No skolas

Matemātika mūsu dzīvē ir klāt ne tikai profesijas apgūšanas un iegūto zināšanu īstenošanas procesā. Tā vai citādi mēs izmantojam zinātņu karalieni gandrīz katrā laika brīdī. Tāpēc matemātiku sāk mācīt diezgan agri. Risinot vienkāršas un sarežģītas problēmas, bērns ne tikai mācās saskaitīt, atņemt un reizināt. Viņš lēnām, sākot no pamatiem, izprot mūsdienu pasaules uzbūvi. Un mēs nerunājam par tehnisko progresu vai spēju pārbaudīt izmaiņas veikalā. Matemātika veido noteiktas domāšanas iezīmes un ietekmē mūsu attieksmi pret pasauli.

Vienkāršākais, grūtākais, vissvarīgākais

Droši vien katrs atcerēsies kaut vienu vakaru, pildot mājasdarbus, kad gribējās izmisīgi gaudot: “Es nesaprotu, kam domāta matemātika!”, mest pie malas nīstās sarežģītās un apnicīgās problēmas un ar draugiem ieskriet pagalmā. Skolā un vēl vēlāk koledžā vecāku un skolotāju apliecinājumi, ka “vēlāk noderēs”, šķiet kaitinošas muļķības. Tomēr izrādās, ka viņiem ir taisnība.

Tieši matemātika un pēc tam fizika māca atrast cēloņu un seku attiecības, veido ieradumu meklēt bēdīgi slaveno “no kurienes aug kājas”. Uzmanība, koncentrēšanās, gribasspēks - tie arī trenējas šo ļoti nīsto problēmu risināšanas procesā. Ja mēs ejam tālāk, matemātisko teoriju izpētes laikā tiek noteikta spēja izdarīt secinājumus no faktiem, paredzēt nākotnes notikumus un arī darīt to pašu. Modelēšana, abstrakcija, dedukcija un indukcija ir visas zinātnes un tajā pašā laikā veidi, kā smadzenes strādā ar informāciju.

Un atkal psiholoģija

Bieži vien tieši matemātika bērnam sniedz atklāsmi, ka pieaugušie nav visvareni un nezina visu. Tas notiek, kad mamma vai tētis, kad tiek lūgts palīdzēt atrisināt problēmu, tikai parausta plecus un paziņo, ka nespēj to izdarīt. Un bērns ir spiests pats meklēt atbildi, kļūdīties un meklēt vēlreiz. Gadās arī, ka vecāki vienkārši atsakās palīdzēt. "Jums tas jādara pašam," viņi saka. Un viņi to dara pareizi. Pēc daudzu stundu mēģinājumiem bērns saņems ne tikai izpildītus mājasdarbus, bet arī spēju patstāvīgi rast risinājumus, atklāt un labot kļūdas. Un tajā ir arī matemātikas loma cilvēka dzīvē.

Protams, neatkarību, spēju pieņemt lēmumus, būt par tiem atbildīgiem un nebaidīties no kļūdām attīsta ne tikai algebras un ģeometrijas stundās. Taču šīm disciplīnām šajā procesā ir nozīmīga loma. Matemātika veicina tādas īpašības kā apņēmība un aktivitāte. Tiesa, daudz kas ir atkarīgs no skolotāja. Nepareizs materiāla izklāsts, pārmērīga stingrība un spiediens, gluži pretēji, var izraisīt bailes no grūtībām un kļūdām (vispirms klasē un pēc tam dzīvē), nevēlēšanos paust savu viedokli un pasivitāti.

Matemātika ikdienas dzīvē

Pēc augstskolas vai koledžas absolvēšanas pieaugušie nebeidz katru dienu risināt matemātikas uzdevumus. Kā noķert vilcienu? Vai kilograms gaļas var pagatavot vakariņas desmit viesiem? Cik daudz kaloriju ir traukā? Cik ilgi darbosies viena spuldze? Šie un daudzi citi jautājumi ir tieši saistīti ar Zinātņu karalieni un nevar tikt atrisināti bez viņas. Izrādās, ka matemātika mūsu dzīvē nemanāmi ir klātesoša gandrīz pastāvīgi. Un visbiežāk mēs to pat nepamanām.

Matemātika sabiedrības un indivīda dzīvē ietekmē ļoti daudzas jomas. Dažas profesijas bez tā nav iedomājamas, daudzas parādījās tikai pateicoties atsevišķu jomu attīstībai. Mūsdienu tehniskais progress ir cieši saistīts ar matemātiskā aparāta sarežģītību un attīstību. Datori un telefoni, lidmašīnas un kosmosa kuģi nekad nebūtu parādījušies, ja cilvēki nebūtu pazinuši zinātņu karalieni. Tomēr ar to matemātikas loma cilvēka dzīvē nebeidzas. Zinātne palīdz bērnam apgūt pasauli, māca viņam efektīvāk mijiedarboties ar to, kā arī veido viņa domāšanu un individuālās rakstura iezīmes. Taču matemātika viena pati ar šādām problēmām netiktu galā. Kā minēts iepriekš, liela nozīme ir materiāla izklāstam un tā cilvēka personības iezīmēm, kurš iepazīstina bērnu ar pasauli.

Efektīvam mūsdienīgam tīmekļa dizainam nevajadzētu būt tikai skaistam, spilgtam attēlam. Tam jābūt vienkāršam un intuitīvam. Ar kādiem līdzekļiem to var panākt? Kā likt apmeklētājam sajust harmoniju un komfortu? Un šeit mums palīdzēs matemātika. Pagaidām apskatīsim, kā web dizainā darbojas daži matemātikas pamatlikumi. Mēs to aplūkosim, izmantojot zelta koeficienta noteikumu, Fibonači skaitļus, piecu elementu likumu, sinusa viļņa svārstības un trešdaļu likumu.

Matemātika ir lieliska. Cilvēkam, kas ir tālu no skaitļiem un vienādojumiem, tas var izklausīties absurdi. Tomēr daudzas skaistākās lietas dabā un pats Visums ir balstītas uz stingrām matemātiskām proporcijām. Pat Aristotelis, viens no autoritatīvākajiem senatnes filozofiem, teica: "Matemātika atklāj kārtību, simetriju un noteiktību, un tie ir vissvarīgākie skaistuma veidi."

Gadsimtiem ilgi matemātika ir izmantota gan mākslā, gan arhitektūrā. Taču matemātika vietņu dizainā tiek izmantota reti. Iespējams, tāpēc, ka ir izplatīts uzskats, ka matemātika un radošums ir nesavienojamas lietas. Lai gan šo viedokli var atspēkot, matemātika ir laba rīks veidojot tīmekļa vietnes. Tomēr šajā jautājumā nevajadzētu paļauties tikai uz matemātiku. Šeit ir vajadzīgs kaut kas cits.

1. Zelta attiecība vai zelta taisnstūris
Zelta griezums (zelta proporcija, dalījums galējā un vidējā proporcijā) ir nepārtrauktas vērtības sadalīšana divās daļās tādā proporcijā, kurā mazākā daļa ir saistīta ar lielāko, jo lielākā ir ar visu vērtību. Daļu attiecību šajā proporcijā izsaka ar iracionālu matemātisko konstanti, kas vienāda ar aptuveni 1,618033987.

Ir vispāratzīts, ka objektus, kas satur “zelta griezumu”, cilvēki uztver kā harmoniskākos. Šeit ir interesants fakts no Vikipēdijas. Zināms, ka Sergejs Eizenšteins mākslīgi uzbūvēja filmu “Kaujas kuģis Potjomkins” pēc zelta griezuma likumiem. Viņš sadalīja lenti piecās daļās.

Pirmajos trijos darbība notiek uz kuģa. Pēdējās divās - Odesā, kur risinās sacelšanās. Šī pāreja uz pilsētu notiek tieši zelta griezuma punktā. Un katrai daļai ir savs lūzums, kas notiek saskaņā ar zelta griezuma likumu.

Tagad pāriesim pie zelta taisnstūra. Šeit viss ir vienkārši. Šādam taisnstūrim blakus esošo malu garumi tiek korelēti saskaņā ar zelta griezuma likumu, t.i. 1:1,618.

Lai izveidotu zelta taisnstūri, vispirms uzzīmējiet kvadrātu (attēlā sarkanā krāsa), pēc tam novelciet līniju no vienas kvadrāta malas vidus līdz pretējam stūrim (attēlā līnija ar bultiņu). Mēs izmantojam šo līniju kā loka rādiusu, kas noteiks taisnstūra augstumu. Tagad pabeidzam taisnstūra zīmēšanu (attēlā zila krāsa).

Apsveriet šo minimālisma dizainu zemāk kā vizuālu piemēru. Tas sastāv no 6 zelta taisnstūriem, kuru izmērs ir 299x185 pikseļi, 3 taisnstūri pēc kārtas. Šo taisnstūru malas ir saistītas saskaņā ar zelta griezuma likumu 299/185 = 1,616.

Ievērojiet lielo vietu ap zelta taisnstūri. Tas rada mierīgu un patīkamu atmosfēru, kurā navigācijas elementi var viegli elpot. Neskatoties uz to, ka tiek izmantotas tikai dažas krāsas un viena veida bloki, visi navigācijas elementi ir intuitīvi un kalpo savam mērķim.

Lai pievienotu jaunu bloku, nepārkāpjot dizaina loģiku, vispiemērotākais ir pievienot blokus trešajā rindā un pārvietoties uz leju līdzīgā veidā.

Lietošanas jomas. Zelta taisnstūru izmantošana dizainā ir labi piemērota dažādām foto galerijām, portfolio vietnēm un vietnēm, kas vērstas uz produktu prezentāciju.

2. Fibonači skaitļi dizainā
Fibonači skaitļi ir matemātiska skaitļu secība. Pēc definīcijas pirmie divi Fibonači skaitļi ir 0 un 1. Katrs nākamais skaitlis ir vienāds ar iepriekšējo divu summu. Ciparu sērija izskatās šādi: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Fibonači skaitļus izmanto mūzikā instrumentu noskaņošanai, arhitektūrā harmonisku proporciju aprēķināšanai, piemēram, telpas augstuma attiecību pret sienu apdares augstumu ar dažādiem materiāliem. Attālumi starp lapām (vai zariem) uz auga stumbra ir aptuveni saistīti ar Fibonači skaitļiem.

Galvenā Fibonači skaitļu pielietojuma joma dizainā ir bloku lieluma noteikšana ar galveno saturu (konteineri) un sānu joslām. Metodes būtība ir šāda. Konteinera bāzes platums tiek ņemts, piemēram, 90 pikseļi un secīgi reizināts ar skaitļiem no Fibonači sērijas. Pamatojoties uz šiem aprēķiniem, tiek izveidots vietnes režģis. Apskatīsim piemēru.

Lapa ir sadalīta trīs kolonnās. Konteinera pamatnes platums ir 90 pikseļi. Tad pirmā kolonna ir 180 pikseļu plata (90 x 2), otrā kolonna ir 270 pikseļu plata (90 x 3), bet trešā kolonna ir 720 pikseļu plata (90 x 8). Arī fonta lielums atbilst Fibonači sērijai. Galvenes fonta izmērs ir 55 pikseļi, sadaļas fonts ir 34 pikseļi un teksta fonts ir 21 pikseļi.

Ja vietnei ir fiksēts platums, piemēram, 1000 pikseļi, tad Fibonači skaitļus nav īpaši ērti lietot. Tā kā Fibonači sērijas skaitlim tuvākais 1000 ir 987 (..., 610, 987, 1597...), tad tieši no šī skaitļa būs jāveic vietnes bloku platuma aprēķini. Šādās situācijās vislabāk ir izmantot Zelta koeficienta likumu (1000 x 0,618 = 618 pikseļi) un ar to noteikt bloku platumu.

Lietošanas jomas. Fibonači skaitļi ir vislabāk piemēroti emuāru dizainam un žurnālu izkārtojumiem.

3. Pieci elementi jeb Kundli dizains
Vēl viens interesants matemātikas piemērs dizainā ir tehnika, kuras pamatā ir Indijas Kundli horoskopa sastādīšanas noteikumi. Pamats šeit ir šāds attēls. Tiek uzzīmēts kvadrāts, tajā ievilktas divas diagonāles, savienojot pretējos stūrus, tad līnijas savieno kvadrāta blakus malu centrus.

Laukuma iekšpusē redzam četrus dimantus. Tas ir pamats piecu dizaina elementu ievietošanai lapā.

Tālāk sniegtais vietnes dizaina piemērs ir balstīts uz Kundli ģeometriju. Šis izkārtojums var būt piemērots vienas lapas vizītkaršu vietnei ar interaktīviem dizaina elementiem, kuru pamatā ir jQuery tehnoloģija.

Turklāt šis izkārtojums var viegli pārvērsties par vietni ar trīs kolonnu izkārtojumu ar galveni un kājeni.

Lietošanas jomas.Šis dizains ir vispiemērotākais portfeļa vietnēm un vietnēm, kas vērstas uz produktu demonstrēšanu.

4. Sinusoidālās svārstības
Ja vēlaties dažādību, tad nemaz nav nepieciešams ievērot zelta griezuma un Fibonači skaitļu pamatnoteikumus. Varat eksperimentēt ar citām labi zināmām formulām.

Apskatīsim, kā izveidosies vietnes izkārtojums, pamatojoties uz sinusoīda svārstībām, matemātisku funkciju, kas apraksta atkārtotas svārstības. Zemāk esošajā attēlā ir parādīts vienkāršas un oriģinālas vienas lapas vietnes piemērs.

Vai arī cits variants. Izkārtojums, kas sastāv no galvenes, piecām kolonnām un kājenes. Šādu vietni var arī uzlabot ar JQuery rīka padomiem, lai padarītu to interaktīvāku.

Lietošanas jomas.Šis dizains ir optimāls vietnēm, kurās ir jāatspoguļo notikumu hronoloģija. Vispiemērotākais horizontālajai navigācijai.

5. Trešdaļas noteikums
Šis noteikums nosaka, ka attēls ir jāsadala deviņās vienādās daļās ar divām horizontālām un divām vertikālām līnijām. Un visiem svarīgajiem kompozīcijas elementiem jābūt izvietotiem pa šīm līnijām vai to krustpunktos.

Šajā piemērā divi no četriem krustojumiem satur vissvarīgāko informāciju. Apzīmēts ar rozā kvadrātiņiem. Un navigācijas bloks atrodas tieši pa otro horizontālo līniju.

Dažreiz šķiet, ka mūsu pasaule ir vienkārša un saprotama. Patiesībā tas ir lielais Visuma noslēpums, kas radīja tik perfektu planētu. Vai varbūt to ir radījis kāds, kurš droši vien zina, ko dara? Pie šī jautājuma strādā mūsu laika lielākie prāti.

Katru reizi viņi nonāk pie secinājuma, ka nav iespējams radīt visu, kas mums ir bez Augstākā prāta. Cik ārkārtēja, sarežģīta un tajā pašā laikā vienkārša un spontāna ir mūsu planēta Zeme! Apkārtējā pasaule ir pārsteidzoša ar saviem noteikumiem, formām un krāsām.

Dabas likumi

Pirmā lieta, kurai varat pievērst uzmanību uz mūsu milzīgās un apbrīnojamās planētas, ir tā, ka tā ir sastopama visās apkārtējās pasaules formās, un tā ir arī skaistuma, idealitātes un proporcionalitātes pamatprincips. Dabā tas nav nekas cits kā matemātika.

Jēdziens "simetrija" nozīmē harmoniju, pareizību. Šī ir apkārtējās realitātes īpašība, kas sistematizē fragmentus un pārvērš tos vienotā veselumā. Jau senajā Grieķijā šī likuma pazīmes sāka pamanīt pirmo reizi. Piemēram, Platons uzskatīja, ka skaistums parādās tikai simetrijas un proporcionalitātes rezultātā. Patiesībā, ja mēs skatāmies uz objektiem, kas ir proporcionāli, pareizi un pilnīgi, tad mūsu iekšējais stāvoklis būs skaists.

Matemātikas likumi dzīvajā un nedzīvajā dabā

Apskatīsim jebkuru radību, piemēram, vispilnīgāko – cilvēku. Mēs redzēsim ķermeņa uzbūvi, kas abās pusēs izskatās vienādi. Varat arī uzskaitīt daudzus piemērus, piemēram, kukaiņus, dzīvniekus, jūras dzīvi, putnus. Katrai sugai ir sava krāsa.

Ja ir kāds raksts vai dizains, ir zināms, ka tas atspoguļojas ap centra līniju. Visi organismi ir radīti, pateicoties Visuma noteikumiem. Šādus matemātiskus modeļus var izsekot arī nedzīvajā dabā.

Ja pievēršat uzmanību visām parādībām, piemēram, viesuļvētrai, varavīksnei, augiem, sniegpārslām, tajās var atrast daudz kopīga. Nosacīti koka lapa ir sadalīta uz pusēm, un katra daļa būs iepriekšējās atspulgs.

Ja par piemēru ņemam tornado, kas paceļas vertikāli un izskatās kā piltuve, tad arī to var sadalīt divās absolūti identiskās daļās. Simetrijas fenomenu var atrast dienas un nakts, gadalaiku maiņā. Apkārtējās pasaules likumi ir matemātika dabā, kurai ir sava ideāla sistēma. Uz tā balstās visa Visuma radīšanas koncepcija.

Varavīksne

Mēs bieži nedomājam par dabas parādībām. Sniga vai lija lietus, iznāca saule vai dārdēja pērkons - ierastais mainīgo laika apstākļu stāvoklis. Apsveriet daudzkrāsaino loku, ko parasti var atrast pēc nokrišņiem. Varavīksne debesīs ir pārsteidzoša dabas parādība, ko pavada visu krāsu spektrs, kas redzams tikai cilvēka acij. Tas notiek tāpēc, ka saules stari iziet cauri aizejošajam mākonim. Katra lietus lāse kalpo kā prizma, kurai ir optiskās īpašības. Mēs varam teikt, ka katrs piliens ir maza varavīksne.

Izejot cauri ūdens barjerai, stari maina savu sākotnējo krāsu. Katrai gaismas straumei ir noteikts garums un nokrāsa. Tāpēc mūsu acis uztver varavīksni kā tik krāsainu. Ļaujiet mums atzīmēt interesantu faktu, ka šo parādību var redzēt tikai cilvēki. Jo tā ir tikai ilūzija.

Varavīksnes veidi

1. Visizplatītākās ir saules veidotās varavīksnes. Tā ir spilgtākā no visām šķirnēm. Sastāv no septiņām pamatkrāsām: sarkana oranža, dzeltena, zaļa, zila, indigo, violeta. Bet, ja mēs skatāmies uz detaļām, ir daudz vairāk toņu, nekā mūsu acis spēj saskatīt.
2. Mēness radīta varavīksne notiek naktī. Tiek uzskatīts, ka to vienmēr var redzēt. Bet, kā liecina prakse, šī parādība galvenokārt tiek novērota tikai lietainos apgabalos vai lielu ūdenskritumu tuvumā. Mēness varavīksnes krāsas ir ļoti blāvas. Tos paredzēts izmeklēt tikai ar speciālas aparatūras palīdzību. Bet pat ar to mūsu acs var izdalīt tikai baltu sloksni.
3. Varavīksne, kas parādās miglas rezultātā, ir kā plaša spīdoša gaismas arka. Dažreiz šis veids tiek sajaukts ar iepriekšējo. Krāsa var būt oranža no augšas un violeta nokrāsa apakšā. Saules stari, kas iet cauri miglai, veido skaistu dabas parādību.
4. debesīs parādās ārkārtīgi reti. Tas nav līdzīgs iepriekšējiem veidiem savā horizontālajā formā. Parādība iespējama tikai virs spalvu mākoņiem. Parasti tie stiepjas 8-10 kilometru augstumā. Leņķim, kurā varavīksne parādīsies visā savā krāšņumā, jābūt lielākam par 58 grādiem. Krāsas parasti paliek tādas pašas kā saules varavīksnē.

Zelta koeficients (1,618)

Ideālu proporcionalitāti visbiežāk var atrast dzīvnieku pasaulē. Viņiem tiek piešķirta proporcija, kas ir vienāda ar PHI skaitļa sakni, kas atbilst vienam. Šī attiecība ir visu planētas dzīvnieku savienojošais fakts. Senatnes dižie prāti šo skaitli sauca par dievišķo proporciju. To var saukt arī par zelta griezumu.

Šis noteikums pilnībā atbilst cilvēka struktūras harmonijai. Piemēram, ja jūs noteiksiet attālumu starp acīm un uzacīm, tas būs vienāds ar dievišķo konstanti.

Zelta griezums ir piemērs tam, cik liela nozīme dabā ir matemātikai, kuras likumu sāka ievērot dizaineri, mākslinieki, arhitekti, skaistu un perfektu lietu veidotāji. Viņi ar dievišķās konstantes palīdzību rada savus darinājumus, kuros ir līdzsvars, harmonija un ir patīkami uz tiem skatīties. Mūsu prāts spēj uzskatīt par skaistām tās lietas, priekšmetus, parādības, kurās ir nevienlīdzīga daļu attiecība. Mūsu smadzenes zelta griezumu sauc par proporcionalitāti.

DNS spirāle

Kā pareizi atzīmēja vācu zinātnieks Hugo Veils, simetrijas saknes radās matemātikā. Daudzi atzīmēja ģeometrisko formu pilnību un pievērsa tām uzmanību. Piemēram, šūnveida ir nekas vairāk kā sešstūris, ko radījusi pati daba. Varat arī pievērst uzmanību egļu čiekuriem, kuriem ir cilindriska forma. Arī apkārtējā pasaulē bieži sastopamas spirāles: lielu un mazu mājlopu ragi, gliemju čaumalas, DNS molekulas.

Radīts pēc zelta griezuma principa. Tā ir savienojošā saikne starp materiālā ķermeņa diagrammu un tā reālo attēlu. Un, ja ņemam vērā smadzenes, tās nav nekas vairāk kā vadītājs starp ķermeni un prātu. Intelekts savieno dzīvi un tās izpausmes formu un ļauj formā ietvertajai dzīvībai izzināt sevi. Ar tā palīdzību cilvēcei ir iespējams izprast apkārtējo planētu, meklēt tajā modeļus, kurus pēc tam var pielietot iekšējās pasaules izpētē.

Sadalījums dabā

Šūnu mitoze sastāv no četrām fāzēm:

• Profāze. Kodols tajā palielinās. Parādās hromosomas, kuras sāk savīties spirālē un pārvēršas savā parastajā formā. Tiek izveidota vieta šūnu dalīšanai. Fāzes beigās kodols un tā apvalks izšķīst, un hromosomas ieplūst citoplazmā. Šis ir garākais sadalīšanas posms.
• Metafāze. Šeit beidzas hromosomu spirāle, un tās veido metafāzes plāksni. Hromatīdi ir novietoti viens pret otru, gatavojoties sadalīšanai. Starp tiem parādās atvienošanas vieta - vārpsta. Tas noslēdz otro posmu.

• Anafāze. Hromatīdi atšķiras pretējos virzienos. Tagad šūnai ir divi hromosomu komplekti to dalīšanās dēļ. Šis posms ir ļoti īss.
• Telofāze. Katrā šūnas pusē veidojas kodols, kura ietvaros veidojas kodols. Citoplazma tiek aktīvi atdalīta. Vārpsta pamazām pazūd.

Mitozes nozīme

Pateicoties unikālajai dalīšanas metodei, katrai nākamajai šūnai pēc reprodukcijas ir tāds pats gēnu sastāvs kā tās mātei. Abas šūnas saņem vienādu hromosomu sastāvu. To nevarētu izdarīt bez tādas zinātnes kā ģeometrija. Mitozes progresēšana ir svarīga, jo tas ir princips, pēc kura visas šūnas vairojas.

No kurienes rodas mutācijas?

Šis process nodrošina pastāvīgu hromosomu un ģenētisko materiālu piegādi katrā šūnā. Mitozes dēļ ķermenis attīstās, vairojas un atjaunojas. Dažu indu darbības traucējumu gadījumā hromosomas var nesadalīties uz pusēm vai arī tām var būt strukturāli traucējumi. Tas būs skaidrs sākuma mutāciju rādītājs.

Summējot

Kas kopīgs matemātikai un dabai? Atbildi uz šo jautājumu atradīsit mūsu rakstā. Un, ja iedziļināmies, jāsaka, ka, pētot apkārtējo pasauli, cilvēks iepazīst sevi. Bez Tā, kurš dzemdēja visu dzīvo, nekas nebūtu varējis notikt. Daba ir tikai harmonijā, stingri ievērojot tās likumus. Vai tas viss ir iespējams bez iemesla?

Citējam zinātnieka, filozofa, matemātiķa un fiziķa Anrī Puankarē teikto, kurš tāpat kā neviens cits var atbildēt uz jautājumu, vai matemātika dabā ir patiesi fundamentāla. Dažiem materiālistiem šāda argumentācija var nepatikt, taču maz ticams, ka viņi to varētu atspēkot. Puankarē saka, ka harmonija, ko cilvēka prāts vēlas atklāt dabā, nevar pastāvēt ārpus tās. kas ir klātesošs vismaz dažu indivīdu prātos, var būt pieejams visai cilvēcei. Saikni, kas apvieno garīgo darbību, sauc par pasaules harmoniju. Pēdējā laikā ir bijuši milzīgi virzieni uz šādu procesu, taču tie ir ļoti nelieli. Šīm saitēm, kas savieno Visumu un indivīdu, vajadzētu būt vērtīgām jebkura cilvēka prātam, kas ir jutīgs pret šiem procesiem.

Noslēgumā mēģināsim īsi raksturot matemātikas vispārīgos attīstības modeļus.

1. Matemātika nav viena vēsturiska laikmeta, vienas tautas radīšana; tas ir vairāku laikmetu produkts, daudzu paaudžu darba produkts. Radās tās pirmie jēdzieni un noteikumi

kā mēs redzējām, senos laikos un jau pirms vairāk nekā diviem tūkstošiem gadu tie tika apvienoti harmoniskā sistēmā. Neskatoties uz visām matemātikas pārvērtībām, tās jēdzieni un secinājumi tiek saglabāti, pārejot no viena laikmeta uz otru, piemēram, aritmētikas likumi vai Pitagora teorēma.

Jaunās teorijas ietver iepriekšējos sasniegumus, tos precizējot, papildinot un vispārinot.

Tajā pašā laikā, kā redzams iepriekš sniegtajā īsajā matemātikas vēstures izklāstā, tās attīstību ne tikai nevar reducēt uz vienkāršu jaunu teorēmu uzkrāšanu, bet tā ietver būtiskas, kvalitatīvas izmaiņas. Attiecīgi matemātikas attīstība ir sadalīta vairākos periodos, kuru pārejas precīzi norāda tik fundamentālas izmaiņas pašā šīs zinātnes priekšmetā vai struktūrā.

Matemātika savā sfērā ietver visas jaunās realitātes kvantitatīvo attiecību jomas. Tajā pašā laikā vissvarīgākais matemātikas priekšmets ir bijis un paliek telpiskās formas un kvantitatīvās attiecības šo vārdu vienkāršākajā, vistiešākajā nozīmē, un matemātiskā izpratne par jauniem sakariem un attiecībām neizbēgami rodas, pamatojoties uz un saistībā ar jau izveidota kvantitatīvo un telpisko zinātnisko jēdzienu sistēma.

Visbeidzot, rezultātu uzkrāšana matemātikā obligāti ietver gan pacelšanos uz jauniem abstrakcijas līmeņiem, jauniem vispārinošiem jēdzieniem, gan padziļināšanu pamatu un sākotnējo jēdzienu analīzē.

Tāpat kā ozols savā varenajā augumā sabiezina vecos zarus ar jauniem slāņiem, met ārā jaunus zarus, stiepjas uz augšu un padziļinās ar saknēm uz leju, tā matemātika savā attīstībā uzkrāj jaunu materiālu savās jau iedibinātajās platībās, veido jaunus virzienus, paceļas augšup. uz jauniem abstrakcijas augstumiem un iedziļinās tās pamatos.

2. Matemātikas priekšmets ir realitātes reālās formas un attiecības, taču, kā teica Engelss, lai šīs formas un attiecības pētītu to tīrā veidā, tās ir pilnībā jāatdala no satura, atstājot to malā kā kaut kas vienaldzīgs. Tomēr formas un attiecības nepastāv ārpus satura, matemātiskās formas un attiecības nevar būt absolūti vienaldzīgas pret saturu. Tāpēc matemātika, kas pēc savas būtības cenšas panākt šādu atdalīšanu, cenšas sasniegt neiespējamo. Tā ir būtiska pretruna pašā matemātikas būtībā. Tā ir matemātikai raksturīga vispārējās izziņas pretrunas izpausme. Katras parādības, katras puses, katra realitātes mirkļa atspoguļojums ar domu to rupjina, vienkāršo, izraujot no kopējās dabas saiknes. Kad cilvēki, pētot telpas īpašības, konstatēja, ka tai ir Eiklīda ģeometrija, kas ir izņēmums

nozīmīgs izziņas akts, taču tajā bija arī malds: telpas reālās īpašības tika [ņemtas vienkāršotā, shematiskā veidā, abstrakcijā no matērijas. Bet bez tā ģeometrijas vienkārši nebūtu, un, pamatojoties uz šo abstrakciju (gan no tās iekšējās izpētes, gan no matemātisko rezultātu salīdzināšanas ar jauniem datiem no citām zinātnēm), dzima un nostiprinājās jaunas ģeometriskās teorijas.

Šīs pretrunas pastāvīgā atrisināšana un atjaunošana izziņas posmos, kas arvien tuvāki realitātei, veido izziņas attīstības būtību. Šajā gadījumā noteicošais, protams, ir zināšanu pozitīvais saturs, absolūtās patiesības elements tajā. Zināšanas virzās pa augšupejošu līniju un neiezīmē laiku, vienkārši sajaucas ar kļūdu. Zināšanu kustība ir pastāvīga to neprecizitātes un ierobežojumu pārvarēšana.

Šī galvenā pretruna ietver citus. Mēs to redzējām diskrēta un nepārtraukta pretstatu piemērā. (Dabā starp tiem nav absolūtas plaisas, un to atdalīšana matemātikā neizbēgami radīja nepieciešamību radīt arvien jaunus jēdzienus, kas dziļāk atspoguļo realitāti un vienlaikus pārvarētu esošās matemātikas teorijas iekšējās nepilnības). Tieši tāpat matemātikā kā tās fundamentālās pretrunas izpausmes parādās galīgā un bezgalīgā, abstraktā un konkrētā, formas un satura uc pretrunas. Taču tās izšķirošā izpausme ir tāda, ka, abstrahējoties no konkrētā, griežoties savu abstrakto jēdzienu lokā, matemātika tādējādi tiek nošķirta no eksperimenta un prakses, un tajā pašā laikā tā ir tikai zinātne (t.i., tai ir kognitīva vērtība), ciktāl tā balstās. uz praksi, jo izrādās, ka tā nav tīra, bet lietišķa matemātika. Hēgeliski runājot, tīrā matemātika pastāvīgi “noliedz” sevi kā tīru matemātiku, bez tā tai nevar būt zinātniska nozīme, tā nevar attīstīties, nevar pārvarēt grūtības, kas tajā neizbēgami rodas.

Formālajā formā matemātiskās teorijas ir pretstatas reālajam saturam kā dažas konkrētu secinājumu shēmas. Šajā gadījumā matemātika darbojas kā metode dabaszinātņu kvantitatīvo likumu formulēšanai, kā aparāts savu teoriju attīstīšanai, kā līdzeklis dabaszinātņu un tehnoloģiju problēmu risināšanai. Tīras matemātikas nozīme pašreizējā posmā galvenokārt ir saistīta ar matemātisko metodi. Un tāpat kā katra metode pastāv un attīstās nevis pati par sevi, bet tikai uz tās pielietojuma pamata, saistībā ar saturu, kuram tā tiek pielietota, tā arī matemātika nevar pastāvēt un attīstīties bez pielietojumiem. Šeit atkal atklājas pretstatu vienotība: vispārīgā metode ir pretstatā konkrētai problēmai kā tās risināšanas līdzeklim, bet pati rodas no konkrēta materiāla vispārinājuma un pastāv.

izstrādā un rod savu pamatojumu tikai konkrētu problēmu risināšanā.

3. Sociālajai praksei ir izšķiroša loma matemātikas attīstībā trīs aspektos. Tas rada jaunas problēmas matemātikai, stimulē tās attīstību vienā vai otrā virzienā un sniedz kritēriju secinājumu patiesumam.

To var ļoti skaidri redzēt analīzes parādīšanās laikā. Pirmkārt, mehānikas un tehnoloģiju attīstība radīja problēmu izpētīt mainīgo lielumu atkarības to vispārējā formā. Arhimēds, pietuvojies diferenciāl- un integrālrēķinam, tomēr palika statikas problēmu ietvaros, savukārt mūsdienās tieši kustības izpēte radīja mainīgā un funkcijas jēdzienus un lika formulēt analīzi. Ņūtons nevarēja attīstīt mehāniku, neizstrādājot atbilstošu matemātisko metodi.

Otrkārt, tieši sociālās ražošanas vajadzības mudināja formulēt un atrisināt visas šīs problēmas. Ne senajā, ne viduslaiku sabiedrībā šie stimuli nepastāvēja. Visbeidzot, ir ļoti raksturīgi, ka matemātiskā analīze, sākot ar to, atrada pamatojumu saviem secinājumiem tieši lietojumos. Tas ir vienīgais iemesls, kāpēc tas varēja attīstīties bez tām stingrām tā pamatjēdzienu definīcijām (mainīgais, funkcija, robeža), kas tika dotas vēlāk. Analīzes patiesumu noteica pielietojumi mehānikā, fizikā un tehnoloģijās.

Iepriekš minētais attiecas uz visiem matemātikas attīstības periodiem. Kopš 17. gs. Vistiešākā ietekme uz tās attīstību kopā ar mehāniku ir teorētiskajai fizikai un jauno tehnoloģiju problēmām. Nepārtrauktības mehānika un pēc tam lauka teorija (siltuma vadītspēja, elektrība, magnētisms, gravitācijas lauks) virza daļēju diferenciālvienādojumu teorijas attīstību. Molekulārās teorijas un statistiskās fizikas attīstība kopumā, sākot no pagājušā gadsimta beigām, kalpoja par nozīmīgu stimulu varbūtību teorijas, īpaši nejaušo procesu teorijas, attīstībai. Relativitātes teorijai ar tās analītiskajām metodēm un vispārinājumiem bija izšķiroša loma Rīmaņa ģeometrijas attīstībā.

Pašlaik jaunu matemātisko teoriju, piemēram, funkcionālās analīzes uc attīstību veicina kvantu mehānikas un elektrodinamikas problēmas, datortehnoloģiju problēmas, fizikas un tehnoloģiju statistikas jautājumi utt., utt. Fizika un tehnoloģijas ne tikai rada jaunus izaicinājumus matemātikas problēmām, virza to pretī jauniem pētniecības priekšmetiem, bet arī modina tiem nepieciešamo matemātikas nozaru attīstību, kas sākotnēji attīstījās lielākā mērā sevī, kā tas bija ar Rīmaņa ģeometriju. Īsāk sakot, zinātnes intensīvai attīstībai ir nepieciešams, lai tā ne tikai pieietu jaunu problēmu risināšanai, bet arī tiktu uzspiesta nepieciešamība tās risināt.

sabiedrības attīstības vajadzībām. Matemātikā nesen ir radušās daudzas teorijas, taču tikai tās ir izstrādātas un stingri iekļautas zinātnē, kuras ir atradušas savu pielietojumu dabaszinātnēs un tehnoloģijās vai spēlējušas svarīgu vispārinājumu lomu tām teorijām, kurām ir šāds pielietojums. Tajā pašā laikā citas teorijas paliek bez kustības, piemēram, dažas rafinētas ģeometriskās teorijas (ne-desarguesa, ne-arhimēda ģeometrijas), kas nav atradušas nozīmīgu pielietojumu.

Matemātisko secinājumu patiesība atrod savu galīgo pamatu nevis vispārīgās definīcijās un aksiomās, nevis formālajā pierādījumu stingrībā, bet gan reālos lietojumos, tas ir, galu galā praksē.

Kopumā matemātikas attīstība galvenokārt ir jāsaprot kā tās priekšmeta loģikas mijiedarbības rezultāts, kas atspoguļojas pašas matemātikas iekšējā loģikā, ražošanas ietekmē un sakaros ar dabaszinātnēm. Šī atšķirība seko sarežģītiem pretstatu cīņas ceļiem, ieskaitot būtiskas izmaiņas matemātikas pamatsaturā un formās. Saturiski matemātikas attīstību nosaka tās priekšmets, bet to galvenokārt un galu galā stimulē ražošanas vajadzības. Tas ir matemātikas attīstības pamatmodelis.

Protams, mēs nedrīkstam aizmirst, ka mēs runājam tikai par pamata modeli un ka saikne starp matemātiku un ražošanu, vispārīgi runājot, ir sarežģīta. No iepriekš teiktā ir skaidrs, ka būtu naivi mēģināt attaisnot jebkuras matemātiskās teorijas rašanos ar tiešu “ražošanas kārtību”. Turklāt matemātikai, tāpat kā jebkurai zinātnei, ir relatīva neatkarība, sava iekšējā loģika, kas atspoguļo, kā mēs uzsvērām, objektīvo loģiku, t.i., tās priekšmeta regularitāti.

4. Matemātika vienmēr ir piedzīvojusi visnozīmīgāko ne tikai sociālās ražošanas, bet arī visu sociālo apstākļu ietekmi kopumā. Tās spožais progress senās Grieķijas uzplaukuma laikmetā, algebras panākumi Itālijā renesanses laikā, analīzes attīstība laikmetā, kas sekoja Anglijas revolūcijai, matemātikas panākumi Francijā laika posmā līdzās Francijas revolūcijai. - tas viss pārliecinoši parāda matemātikas progresa nesaraujamo saistību ar sabiedrības vispārējo tehnisko, kultūras, politisko progresu.

Tas ir skaidri redzams arī matemātikas attīstībā Krievijā. Neatkarīgas krievu matemātikas skolas veidošanās, kas nāk no Lobačevska, Ostrogradska un Čebiševa, nav nošķirama no visas Krievijas sabiedrības progresa. Lobačevska laiks ir Puškina laiks,

Glinka, decembristu laiks un matemātikas uzplaukums bija viens no vispārējā uzplaukuma elementiem.

Vēl jo pārliecinošāka ir sociālās attīstības ietekme laika posmā pēc Lielās Oktobra sociālistiskās revolūcijas, kad viens pēc otra pārsteidzošā ātrumā parādījās fundamentālas nozīmes pētījumi daudzos virzienos: kopu teorijā, topoloģijā, skaitļu teorijā, varbūtību teorijā, teorijā. diferenciālvienādojumi, funkcionālā analīze, algebra, ģeometrija.

Visbeidzot, matemātiku vienmēr ir un joprojām būtiski ietekmē ideoloģija. Tāpat kā jebkurā zinātnē, matemātikas objektīvo saturu matemātiķi un filozofi uztver un interpretē vienas vai citas ideoloģijas ietvaros.

Īsāk sakot, zinātnes objektīvais saturs vienmēr iekļaujas vienā vai citā ideoloģiskā formā; šo dialektisko pretstatu – objektīvā satura un ideoloģisko formu – vienotībai un cīņai matemātikā, tāpat kā jebkurā zinātnē, ir liela nozīme tās attīstībā.

Cīņa starp materiālismu, kas atbilst zinātnes objektīvajam saturam, un ideālismu, kas ir pretrunā ar šo saturu un deformē tā izpratni, iet cauri visai matemātikas vēsturei. Uz šo cīņu skaidri norādīja jau senajā Grieķijā, kur Pitagora, Sokrata un Platona ideālisms pretojās Talsa, Demokrita un citu grieķu matemātiku radošo filozofu materiālismam. Attīstoties vergu sistēmai, sabiedrības elite atdalījās no līdzdalības ražošanā, uzskatot to par zemākās šķiras likteni, un tas radīja “tīrās” zinātnes atdalīšanu no prakses. Tikai tīri teorētiskā ģeometrija tika atzīta par patiesa filozofa uzmanības cienīgu. Raksturīgi, ka Platons uzskatīja, ka topošie pētījumi par dažām mehāniskām līknēm un pat koniskiem griezumiem paliek ārpus ģeometrijas robežām, jo ​​tie "neieved mūs saskarsmē ar mūžīgām un bezķermeniskām idejām" un "nepieciešams izmantot vulgāra instrumentus. amatniecība.”

Spilgts piemērs materiālisma cīņai pret ideālismu matemātikā ir Lobačevska darbība, kurš izvirzīja un aizstāvēja materiālistisko matemātikas izpratni pret ideālistiskajiem kantiānisma uzskatiem.

Krievu matemātikas skolai kopumā raksturīga materiālistiska tradīcija. Tādējādi Čebiševs skaidri uzsvēra prakses izšķirošo nozīmi, un Ļapunovs krievu matemātikas skolas stilu izteica ar šādiem ievērojamiem vārdiem: “No pielietojuma viedokļa īpaši svarīgu jautājumu detalizēta izstrāde un tajā pašā laikā īpaši prezentējot. teorētiskās grūtības, kas prasa jaunu metožu izgudrošanu un pacelšanos uz zinātnes principiem, pēc tam vispārinot secinājumus un tādējādi radot vairāk vai mazāk vispārīgu teoriju. Vispārinājumi un abstrakcijas nav paši par sevi, bet gan saistībā ar konkrētu materiālu

teorēmas un teorijas nevis pašas par sevi, bet vispārējā zinātnes saiknē, kas galu galā noved pie prakses - tas izrādās patiesībā svarīgi un daudzsološi.

Tie bija arī tādu izcilu zinātnieku kā Gauss un Rīmans centieni.

Taču, attīstoties kapitālismam Eiropā, materiālistiskus uzskatus, kas atspoguļoja 16. – 19. gadsimta sākuma uzlecošās buržuāzijas attīstīto ideoloģiju, sāka aizstāt ideālistiski uzskati. Piemēram, Kantors (1846-1918), veidojot bezgalīgo kopu teoriju, tieši atsaucās uz Dievu, runājot garā, ka bezgalīgām kopām dievišķajā prātā ir absolūta eksistence. Lielākais franču matemātiķis 19. gadsimta beigās un 20. gadsimta sākumā. Puankarē izvirzīja ideālistisku “konvencionālisma” jēdzienu, saskaņā ar kuru matemātika ir konvencionālu vienošanos shēma, kas pieņemta pieredzes daudzveidības apraksta ērtībai. Tādējādi, pēc Puankarē domām, Eiklīda ģeometrijas aksiomas nav nekas vairāk kā nosacītas vienošanās un to nozīmi nosaka ērtības un vienkāršība, bet ne atbilstība realitātei. Tāpēc Puankarē teica, ka, piemēram, fizikā viņi drīzāk atteiksies no gaismas taisnās izplatīšanās likuma, nevis no Eiklīda ģeometrijas. Šo viedokli atspēkoja relativitātes teorijas attīstība, kas, neskatoties uz visu Eiklīda ģeometrijas "vienkāršību" un "ērtību", pilnībā saskanot ar Lobačevska un Rīmaņa materiālistiskajām idejām, lika secināt, ka reālā telpas ģeometrija atšķiras no Eiklīda.

Sakarā ar grūtībām, kas radās kopu teorijā un saistībā ar nepieciešamību analizēt matemātikas pamatjēdzienus, matemātiķu vidū 20. gadsimta sākumā. radās dažādas straumes. Vienotība matemātikas satura izpratnē tika zaudēta; dažādi matemātiķi sāka atšķirīgi raudzīties ne tikai uz vispārējiem zinātnes pamatiem, kā tas bija iepriekš, bet pat sāka atšķirīgi vērtēt atsevišķu konkrētu rezultātu un pierādījumu nozīmi un nozīmi. Secinājumi, kas dažiem šķita jēgpilni un nozīmīgi, tika pasludināti par bezjēdzīgiem un nozīmīgiem. Radās ideālistiskas “loģisma”, “intuīcijas”, “formālisma” u.c. kustības.

Loģisti apgalvo, ka visa matemātika ir izsecināma no loģikas jēdzieniem. Intuīcijas piekritēji matemātikas avotu saskata intuīcijā un piešķir nozīmi tikai intuitīvi uztvertam. Tāpēc jo īpaši viņi pilnībā noliedz Kantora bezgalīgo kopu teorijas nozīmi. Turklāt intuīcijas piekritēji noliedz pat šādu apgalvojumu vienkāršo nozīmi

kā teorēmu, ka katram pakāpju algebriskajam vienādojumam ir saknes. Viņiem šis paziņojums ir tukšs, līdz tiek norādīta sakņu aprēķināšanas metode. Tādējādi matemātikas objektīvās nozīmes pilnīgs noliegums lika intuicionistiem diskreditēt ievērojamu daļu matemātikas sasniegumu kā “bez nozīmes”. Ekstrēmākie no tiem bija tik tālu, ka apgalvoja, ka ir tik daudz matemātiķu, cik matemātiķu.

Mēģinājumu savā veidā glābt matemātiku no šāda veida uzbrukumiem veica mūsu gadsimta sākuma lielākais matemātiķis D. Hilberts. Viņa idejas būtība bija reducēt matemātikas teorijas līdz tīri formālām darbībām ar simboliem saskaņā ar noteiktiem noteikumiem. Aprēķins bija tāds, ka ar šādu pilnīgi formālu pieeju visas grūtības tiktu novērstas, jo matemātikas priekšmets būtu simboli un noteikumi, kā rīkoties ar tiem bez jebkādas saistības ar to nozīmi. Tas ir formālisma uzstādījums matemātikā. Pēc intuīcijas speciālista Brouvera domām, formālistam matemātikas patiesība ir uz papīra, savukārt intuicionistam tā ir matemātiķa galvā.

Tomēr nav grūti redzēt, ka tie abi ir nepareizi, matemātikai, un tajā pašā laikā tas, kas rakstīts uz papīra un ko matemātiķis domā, atspoguļo realitāti, un matemātikas patiesība slēpjas tās atbilstībā objektīvajai realitātei. . Atdalot matemātiku no materiālās realitātes, visas šīs tendences izrādās ideālistiskas.

Hilberta ideju sakāva pati attīstība. Austriešu matemātiķis Gēdels pierādīja, ka pat aritmētiku nevar formalizēt pilnībā, kā bija cerējis Hilberts. Gēdela secinājums skaidri atklāja matemātikas iekšējo dialektiku, kas neļauj nevienu tās jomu izsmelt ar formāliem aprēķiniem. Pat visvienkāršākā dabiskas skaitļu sērijas bezgalība izrādījās neizsmeļama galīga simbolu shēma un noteikumi, kā darboties ar tiem. Tādējādi tika matemātiski pierādīts tas, ko Engelss vispārīgi izteica, rakstot:

"Bezgalība ir pretruna... Šīs pretrunas iznīcināšana būtu bezgalības beigas." Hilberts cerēja iekļaut matemātisko bezgalību ierobežotu shēmu ietvaros un tādējādi novērst visas pretrunas un grūtības. Tas izrādījās neiespējami.

Bet kapitālisma apstākļos konvencionālisms, intuīcionisms, formālisms un citas līdzīgas kustības ne tikai saglabājas, bet tiek papildinātas ar jauniem ideālistisku uzskatu variantiem par matemātiku. Ar matemātikas pamatu loģisko analīzi saistītās teorijas tiek plaši izmantotas dažos jaunos subjektīvā ideālisma variantos. Subjektīvs

ideālisms tagad izmanto matemātiku, jo īpaši matemātisko loģiku, ne mazāk kā fiziku, un tāpēc jautājumi par matemātikas pamatu izpratni kļūst īpaši aktuāli.

Tādējādi matemātikas attīstības grūtības kapitālisma apstākļos izraisīja šīs zinātnes ideoloģisku krīzi, kas pēc pamatiem ir līdzīga fizikas krīzei, kuras būtību savā spožajā darbā “Materiālisms un impērija” noskaidroja Ļeņins. - Kritika." Šī krīze nebūt nenozīmē, ka matemātika kapitālistiskajās valstīs ir pilnībā aizkavējusies savā attīstībā. Vairāki zinātnieki ar nepārprotami ideālistiskām nostādnēm gūst svarīgus, dažkārt izcilus panākumus konkrētu matemātisku problēmu risināšanā un jaunu teoriju izstrādē. Pietiek atsaukties uz spožo matemātiskās loģikas attīstību.

Kapitālisma valstīs plaši izplatītā matemātikas skatījuma fundamentālais trūkums slēpjas tā ideālismā un metafizikā: matemātikas nošķirtībā no realitātes un novārtā pret tās reālo attīstību. Loģistika, intuīcionisms, formālisms un citi līdzīgi virzieni izceļ matemātikā vienu no tās aspektiem - saikni ar loģiku, intuitīvu skaidrību, formālu stingrību utt. - tās nepamatoti pārspīlē, absolutizē tās nozīmi, atdala to no realitātes un aiz tā dziļas analīzes. Viena matemātikas iezīme pati par sevi ir aizmirstība par matemātiku kopumā. Tieši šīs vienpusības dēļ neviens no šiem strāvojumiem ar visu individuālo secinājumu smalkumu un dziļumu nevar novest pie pareizas matemātikas izpratnes. Pretstatā dažādām ideālisma un metafizikas strāvām un nokrāsām, dialektiskais materiālisms matemātiku, tāpat kā visu zinātni kopumā, uzskata par tādu, kāda tā ir, visā tās savienojumu un attīstības bagātībā un sarežģītībā. Un tieši tāpēc, ka dialektiskais materiālisms cenšas izprast visu zinātnes un realitātes saikņu bagātību un sarežģītību, visu tās attīstības sarežģītību, pārejot no vienkāršas pieredzes vispārināšanas uz augstākām abstrakcijām un no tām uz praksi, tieši tāpēc, ka tas pastāvīgi. pati savu pieeju zinātnei vada atbilstoši tās objektīvajam saturam, ar saviem jaunajiem atklājumiem, tieši šī iemesla dēļ un galu galā tikai šī iemesla dēļ tā izrādās vienīgā patiesi zinātniskā filozofija, kas ved uz pareizu zinātnes izpratni vispār un jo īpaši matemātika.