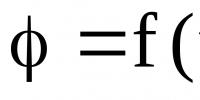Saskaņā ar varbūtības teoriju. Notikumu veidi, notikuma iestāšanās varbūtības tiešais aprēķins

Mācība par likumiem, uz kuriem t.s. nejauši notikumi. Krievu valodā iekļauto svešvārdu vārdnīca. Čudinovs A.N., 1910... Krievu valodas svešvārdu vārdnīca

varbūtības teorija- - [L.G.Sumenko. Angļu krievu informācijas tehnoloģiju vārdnīca. M.: GP TsNIIS, 2003.] Tēmas informācijas tehnoloģija vispārīgi EN varbūtības teorijas varbūtības varbūtības aprēķināšanas teorija ... Tehniskā tulkotāja rokasgrāmata

Varbūtību teorija- ir matemātikas daļa, kas pēta sakarības starp dažādu notikumu varbūtībām (sk. Varbūtība un statistika). Mēs uzskaitām svarīgākās ar šo zinātni saistītās teorēmas. Viena no vairākiem nesaderīgiem notikumiem iestāšanās varbūtība ir vienāda ar ... ... Enciklopēdiskā vārdnīca F.A. Brokhauss un I.A. Efrons

VARBŪTĪBU TEORIJA- matemātiskā zinātne, kas ļauj pēc dažu nejaušu notikumu varbūtībām (sk.) atrast nejaušu notikumu varbūtības, kas saistītas ar k. l. veidā ar pirmo. Mūsdienu TV pamatojoties uz A. N. Kolmogorova aksiomātiku (sk. Aksiomātisko metodi). Uz… … Krievu socioloģiskā enciklopēdija

Varbūtību teorija- matemātikas nozare, kurā pēc uzdotajām dažu nejaušu notikumu varbūtībām tiek atrastas citu notikumu varbūtības, kas kaut kādā veidā saistītas ar pirmo. Varbūtību teorija pēta arī gadījuma lielumus un gadījuma procesus. Viens no galvenajiem…… Mūsdienu dabaszinātņu jēdzieni. Pamatterminu glosārijs

varbūtības teorija- tikimybių teorija statusas T joma fizika atitikmenys: engl. varbūtību teorija vok. Wahrscheinlichkeitstheorie, f rus. varbūtību teorija, f pranc. theorie des probabilités, f … Fizikos terminų žodynas

Varbūtību teorija- ... Vikipēdija

Varbūtību teorija- matemātiskā disciplīna, kas pēta nejaušu parādību modeļus ... Mūsdienu dabaszinātņu pirmsākumi

VARBŪTĪBU TEORIJA- (varbūtības teorija) sk. Varbūtību ... Lielā skaidrojošā socioloģiskā vārdnīca

Varbūtību teorija un tās pielietojumi- (“Varbūtību teorija un tās pielietojumi”), PSRS Zinātņu akadēmijas Matemātikas nodaļas zinātniskais žurnāls. Publicē oriģinālus rakstus un īsus paziņojumus par varbūtību teoriju, matemātiskās statistikas vispārējām problēmām un to pielietojumu dabaszinātnēs un ... ... Lielā padomju enciklopēdija

Grāmatas

• Varbūtību teorija. , Venttsel E.S. Grāmata ir mācību grāmata, kas paredzēta cilvēkiem, kuri pārzina matemātiku parastā vidusskolas kursa ietvaros un interesējas par varbūtību teorijas tehniskajiem pielietojumiem, ... Pirkt par 2056 UAH (tikai Ukrainā)
• Varbūtību teorija. , Wentzel E.S. Grāmata ir mācību grāmata, kas paredzēta cilvēkiem, kuri pārzina matemātiku parastā vidusskolas kursa ietvaros un interesējas par varbūtības teorijas tehniskajiem pielietojumiem ...

Varbūtību teorija ir matemātikas nozare, kas pēta nejaušu parādību modeļus: nejaušus notikumus, gadījuma lielumus, to īpašības un darbības ar tiem.

Ilgu laiku varbūtības teorijai nebija skaidras definīcijas. Tas tika formulēts tikai 1929. gadā. Varbūtību teorijas kā zinātnes rašanās tiek attiecināta uz viduslaikiem un pirmajiem azartspēļu matemātiskās analīzes mēģinājumiem (mest, kauliņi, rulete). 17. gadsimta franču matemātiķi Blēzs Paskāls un Pjērs de Fermā atklāja pirmos varbūtības modeļus, kas rodas, metot kauliņus, pētot azartspēļu laimestu prognozes.

Varbūtības teorija radās kā zinātne no pārliecības, ka noteikti modeļi ir masīvu nejaušu notikumu pamatā. Varbūtību teorija pēta šos modeļus.

Varbūtību teorija nodarbojas ar tādu notikumu izpēti, kuru rašanās nav precīzi zināma. Tas ļauj spriest par dažu notikumu rašanās varbūtības pakāpi salīdzinājumā ar citiem.

Piemēram: nav iespējams viennozīmīgi noteikt monētas galvas vai astes mešanas rezultātu, bet ar atkārtotu mešanu izkrīt aptuveni vienāds skaits galvu un astes, kas nozīmē, ka varbūtība, ka galvas vai astes nokritīs ", ir vienāda līdz 50%.

pārbaudešajā gadījumā tiek saukta noteikta nosacījumu kopuma īstenošana, tas ir, šajā gadījumā, monētas mešana. Izaicinājumu var izspēlēt neierobežotu skaitu reižu. Šajā gadījumā nosacījumu komplekss ietver nejaušības faktorus.

Testa rezultāts ir notikumu. Pasākums notiek:

1. Uzticams (vienmēr notiek pārbaudes rezultātā).
2. Neiespējami (nekad nenotiek).
3. Nejauši (var rasties un var nenotikt testa rezultātā).

Piemēram, metot monētu, neiespējams notikums - monēta nonāks uz malas, nejaušs notikums - "galvu" vai "astes" zaudēšana. Konkrēto testa rezultātu sauc elementārs pasākums. Pārbaudes rezultātā notiek tikai elementāri notikumi. Tiek saukts visu iespējamo, atšķirīgo, specifisko testa rezultātu kopums elementāra pasākumu telpa.

Teorijas pamatjēdzieni

Varbūtība- notikuma iestāšanās iespējamības pakāpe. Ja kāda iespējamā notikuma reāli iestāšanās iemesli ir lielāki par pretējo, tad šo notikumu sauc par iespējamu, pretējā gadījumā – par maz ticamu vai maz ticamu.

Izlases vērtība- šī ir vērtība, kas testa rezultātā var iegūt vienu vai otru vērtību, un iepriekš nav zināms, kura. Piemēram: ugunsdzēsēju depo skaits dienā, trāpījumu skaits ar 10 šāvieniem utt.

Nejaušos mainīgos var iedalīt divās kategorijās.

1. Diskrēts nejaušības lielums tiek izsaukts tāds lielums, kas testa rezultātā ar noteiktu varbūtību var iegūt noteiktas vērtības, veidojot saskaitāmu kopu (kopu, kuras elementus var numurēt). Šis komplekts var būt gan ierobežots, gan bezgalīgs. Piemēram, šāvienu skaits pirms pirmā trāpījuma mērķī ir diskrēts nejaušības lielums, jo šī vērtība var iegūt bezgalīgu, kaut arī saskaitāmu vērtību skaitu.
2. Nepārtraukts gadījuma mainīgais ir lielums, kas var iegūt jebkuru vērtību no kāda ierobežota vai bezgalīga intervāla. Acīmredzot nepārtraukta gadījuma lieluma iespējamo vērtību skaits ir bezgalīgs.

Varbūtības telpa- jēdziens, ko ieviesa A.N. Kolmogorovs 1930. gados, lai formalizētu varbūtības jēdzienu, kas izraisīja strauju varbūtības teorijas kā stingras matemātikas disciplīnas attīstību.

Varbūtības telpa ir trīskārša (dažreiz ierāmēta leņķiekavās: , kur

Šī ir patvaļīga kopa, kuras elementus sauc par elementārajiem notikumiem, rezultātiem vai punktiem;
- apakškopu sigma-algebra, ko sauc par (nejaušiem) notikumiem;
- varbūtības mērs vai varbūtība, t.i. sigma-piedevas ierobežots pasākums tāds, ka .

De Moivre-Laplasa teorēma- viena no ierobežojošajām varbūtības teorijas teorēmām, ko Laplass noteica 1812. gadā. Viņa norāda, ka panākumu skaits, atkārtojot vienu un to pašu nejaušu eksperimentu ar diviem iespējamiem rezultātiem, ir aptuveni normāli sadalīts. Tas ļauj jums atrast aptuvenu varbūtības vērtību.

Ja katram no neatkarīgiem izmēģinājumiem kāda nejauša notikuma iestāšanās varbūtība ir vienāda ar () un ir to izmēģinājumu skaits, kuros tas faktiski notiek, tad nevienlīdzības derīguma varbūtība ir tuva (lieliem ) uz Laplasa integrāļa vērtību.

Sadalījuma funkcija varbūtību teorijā- gadījuma lieluma vai gadījuma vektora sadalījumu raksturojoša funkcija; varbūtība, ka gadījuma lielums X iegūs vērtību, kas ir mazāka vai vienāda ar x, kur x ir patvaļīgs reālais skaitlis. Noteiktos apstākļos tas pilnībā nosaka gadījuma lielumu.

Paredzamā vērtība- gadījuma lieluma vidējā vērtība (tas ir varbūtības teorijā aplūkotais gadījuma lieluma varbūtības sadalījums). Angļu literatūrā to apzīmē ar, krievu valodā -. Statistikā bieži izmanto apzīmējumu.

Dota varbūtības telpa un tajā definēts gadījuma lielums. Tā pēc definīcijas ir izmērāma funkcija. Tad, ja ir Lēbesga integrālis virs telpas , tad to sauc par matemātisko cerību jeb vidējo vērtību un apzīmē ar .

Gadījuma lieluma dispersija- dotā gadījuma lieluma izplatības mērs, t.i., tā novirze no matemātiskās cerības. Norādīts krievu literatūrā un ārzemēs. Statistikā bieži tiek lietots apzīmējums vai. Dispersijas kvadrātsakni sauc par standarta novirzi, standarta novirzi vai standarta izkliedi.

Ļaut būt nejaušam mainīgajam, kas definēts kādā varbūtības telpā. Tad

kur simbols apzīmē matemātisko cerību.

Varbūtību teorijā tiek saukti divi nejauši notikumi neatkarīgs ja viena no tām rašanās nemaina otra rašanās iespējamību. Līdzīgi tiek izsaukti divi nejaušie mainīgie atkarīgi ja viena no tām vērtība ietekmē otra vērtību varbūtību.

Lielo skaitļu likuma vienkāršākā forma ir Bernulli teorēma, kas nosaka, ja notikuma iespējamība visos izmēģinājumos ir vienāda, tad, palielinoties mēģinājumu skaitam, notikuma biežums tiecas uz notikuma varbūtību un pārstāj būt nejaušs.

Lielo skaitļu likums varbūtību teorijā nosaka, ka fiksēta sadalījuma ierobežotas izlases vidējais aritmētiskais ir tuvu šī sadalījuma teorētiskajam vidējam. Atkarībā no konverģences veida izšķir vāju lielo skaitļu likumu, kad notiek varbūtības konverģence, un spēcīgu lielo skaitļu likumu, kad gandrīz noteikti notiek konverģence.

Lielo skaitļu likuma vispārīgā nozīme ir tāda, ka liela skaita identisku un neatkarīgu nejaušības faktoru kopīga darbība noved pie rezultāta, kas robežās nav atkarīgs no nejaušības.

Uz šo īpašību ir balstītas metodes varbūtības noteikšanai, pamatojoties uz ierobežota parauga analīzi. Labs piemērs ir vēlēšanu rezultātu prognozēšana, pamatojoties uz vēlētāju izlases aptauju.

Centrālo robežu teorēmas- Teorēmu klase varbūtības teorijā, kurā teikts, ka pietiekami liela skaita vāji atkarīgu gadījuma lielumu summai, kuriem ir aptuveni vienāda skala (neviens no terminiem nedominē, nedod izšķirošu ieguldījumu summā) ir sadalījums tuvu normāli.

Tā kā daudzi nejaušie mainīgie lietojumos veidojas vairāku vāji atkarīgu nejaušības faktoru ietekmē, to sadalījums tiek uzskatīts par normālu. Šajā gadījumā ir jāievēro nosacījums, ka neviens no faktoriem nav dominējošs. Centrālās robežu teorēmas šajos gadījumos attaisno normālā sadalījuma piemērošanu.

Kad monēta tiek mētāta, var teikt, ka tā piezemēsies heads up, vai varbūtība no tā ir 1/2. Protams, tas nenozīmē, ka, ja monēta tiek izmesta 10 reizes, tā noteikti piezemēsies uz galvām 5 reizes. Ja monēta ir "godīga" un ja tā tiek mētāta daudzas reizes, tad pusi reizes galviņas būs ļoti tuvu. Tādējādi pastāv divu veidu varbūtības: eksperimentāls un teorētiski .

Eksperimentālā un teorētiskā varbūtība

Ja mēs metam monētu daudz reižu — piemēram, 1000 — un saskaitām, cik reižu tā pacelsies, mēs varam noteikt varbūtību, ka tā pacelsies. Ja galvas parādās 503 reizes, mēs varam aprēķināt to parādīšanās varbūtību:
503/1000 vai 0,503.

to eksperimentāls varbūtības definīcija. Šī varbūtības definīcija izriet no novērošanas un datu izpētes, un tā ir diezgan izplatīta un ļoti noderīga. Piemēram, šeit ir dažas varbūtības, kas tika noteiktas eksperimentāli:

1. Iespēja, ka sieviete saslims ar krūts vēzi, ir 1/11.

2. Ja tu skūpstāsi ar kādu, kurš ir saaukstējies, tad varbūtība, ka arī tu saaukstēsies, ir 0,07.

3. Personai, kura tikko iznākusi no cietuma, ir 80% iespēja atgriezties cietumā.

Ja mēs ņemam vērā monētas mešanu un ņemot vērā to, ka tai ir vienlīdz liela iespēja pacelties galvai vai astes, mēs varam aprēķināt varbūtību, ka tiks paceltas galvas: 1/2. Šī ir varbūtības teorētiskā definīcija. Šeit ir dažas citas varbūtības, kas teorētiski noteiktas, izmantojot matemātiku:

1. Ja istabā ir 30 cilvēki, varbūtība, ka diviem no viņiem ir vienāda dzimšanas diena (neskaitot gadu), ir 0,706.

2. Ceļojuma laikā tu satiec kādu un sarunas gaitā atklāj, ka tev ir abpusēja paziņa. Tipiska reakcija: "Tā nevar būt!" Patiesībā šī frāze neder, jo šāda notikuma iespējamība ir diezgan liela – nedaudz virs 22%.

Tāpēc eksperimentālo varbūtību nosaka novērojumi un datu vākšana. Teorētiskās varbūtības nosaka matemātiskā spriešana. Eksperimentālo un teorētisko varbūtību piemēri, piemēram, tie, kas tika apspriesti iepriekš, un jo īpaši tie, kurus mēs negaidām, liek mums saprast, cik svarīgi ir pētīt varbūtību. Jūs varat jautāt: "Kas ir patiesā varbūtība?" Patiesībā tāda nav. Eksperimentāli ir iespējams noteikt varbūtības noteiktās robežās. Tās var sakrist vai nesakrist ar varbūtībām, ko iegūstam teorētiski. Ir situācijas, kurās ir daudz vieglāk definēt vienu varbūtības veidu nekā citu. Piemēram, pietiktu ar teorētiskās varbūtības palīdzību atrast varbūtību saaukstēties.

Eksperimentālo varbūtību aprēķināšana

Vispirms apsveriet varbūtības eksperimentālo definīciju. Pamatprincips, ko izmantojam šādu varbūtību aprēķināšanai, ir šāds.

Princips P (eksperimentāls)

Ja eksperimentā, kurā tiek veikti n novērojumi, situācija vai notikums E notiek m reizes n novērojumos, tad notikuma eksperimentālā varbūtība tiek uzskatīta par P (E) = m/n.

1. piemērs Socioloģiskā aptauja. Tika veikts eksperimentāls pētījums, lai noteiktu kreiļu, labroču un cilvēku skaitu, kuriem abas rokas ir vienādi attīstītas.Rezultāti parādīti grafikā.

a) Nosakiet varbūtību, ka persona ir labā roka.

b) Nosakiet varbūtību, ka persona ir kreilis.

c) Nosakiet varbūtību, ka persona vienādi brīvi pārvalda abas rokas.

d) Lielākajā daļā PBA turnīru ir 120 spēlētāji. Pamatojoties uz šo eksperimentu, cik spēlētāju var būt kreili?

Risinājums

a) Labroču skaits ir 82, kreiļu skaits ir 17, un to, kas vienādi brīvi pārvalda abas rokas, ir 1. Kopējais novērojumu skaits ir 100. Tādējādi iespējamība ka cilvēks ir ar labo roku, ir P
P = 82/100 jeb 0,82 vai 82%.

b) Varbūtība, ka cilvēks ir kreilis, ir P, kur
P = 17/100 vai 0,17 vai 17%.

c) Varbūtība, ka cilvēks vienlīdz brīvi pārvalda abas rokas, ir P, kur
P = 1/100 vai 0,01 vai 1%.

d) 120 boulinga spēlētāji un no (b) varam sagaidīt, ka 17% būs kreili. No šejienes
17% no 120 = 0,17,120 = 20,4,
tas ir, mēs varam sagaidīt aptuveni 20 spēlētājus ar kreiļiem.

2. piemērs Kvalitātes kontrole . Ražotājam ir ļoti svarīgi saglabāt savu produktu kvalitāti augstā līmenī. Faktiski uzņēmumi nolīgst kvalitātes kontroles inspektorus, lai nodrošinātu šo procesu. Mērķis ir atbrīvot minimālo iespējamo defektīvo produktu skaitu. Bet, tā kā uzņēmums katru dienu ražo tūkstošiem vienību, tas nevar atļauties pārbaudīt katru preci, lai noteiktu, vai tai ir defekts vai nē. Lai noskaidrotu, cik procentu produktu ir ar defektiem, uzņēmums pārbauda daudz mazāk preču.
USDA pieprasa, lai 80% sēklu, ko audzētāji pārdod, dīgstu. Lai noteiktu lauksaimniecības uzņēmuma ražoto sēklu kvalitāti, no saražotajām tiek iesētas 500 sēklas. Pēc tam tika aprēķināts, ka uzdīgušas 417 sēklas.

a) Kāda ir varbūtība, ka sēklas uzdīgs?

b) Vai sēklas atbilst valdības standartiem?

Risinājums a) Mēs zinām, ka no 500 iestādītajām sēklām 417 uzdīgušas. Sēklu dīgtspējas varbūtība P, un
P = 417/500 = 0,834 jeb 83,4%.

b) Tā kā uzdīgušo sēklu procentuālais daudzums pārsniedza 80% pēc pieprasījuma, sēklas atbilst valsts standartiem.

3. piemērs TV reitingi. Saskaņā ar statistiku Amerikas Savienotajās Valstīs ir 105 500 000 TV mājsaimniecību. Katru nedēļu tiek apkopota un apstrādāta informācija par programmu skatīšanos. Vienas nedēļas laikā 7 815 000 mājsaimniecību tika noskaņotas uz CBS populāro komēdiju seriālu Everybody Loves Raymond un 8 302 000 mājsaimniecību tika noskaņotas uz NBC hitu Law & Order (avots: Nielsen Media Research). Kāda ir varbūtība, ka vienas mājas televizors konkrētajā nedēļā tiks noregulēts uz "Everybody Loves Raymond"? uz "Likums un kārtība"?

Risinājums Varbūtība, ka vienā mājsaimniecībā televizors ir iestatīts uz "Everybody Loves Raymond" ir P, un
P = 7 815 000/105 500 000 ≈ 0,074 ≈ 7,4%.
Iespēja, ka mājsaimniecības televizors bija iestatīts uz "Likums un kārtība" ir P, un
P = 8 302 000/105 500 000 ≈ 0,079 ≈ 7,9%.
Šos procentus sauc par vērtējumiem.

teorētiskā varbūtība

Pieņemsim, ka mēs veicam eksperimentu, piemēram, metam monētu vai šautriņu, izvelkam kārti no klāja vai pārbaudām produktu kvalitāti uz montāžas līnijas. Katrs iespējamais šāda eksperimenta iznākums tiek saukts Izceļošana . Tiek izsaukta visu iespējamo rezultātu kopa iznākuma telpa . Pasākums tas ir rezultātu kopums, tas ir, rezultātu telpas apakškopa.

4. piemērs Šautriņu mešana. Pieņemsim, ka "šautriņu mešanas" eksperimentā šautra trāpa mērķī. Atrodiet katru no šīm iespējām:

b) Iznākuma telpa

Risinājums
a) Rezultāti ir: sitiens ar melno (H), sarkano (K) un balto (B).

b) Ir iznākuma atstarpe (sit melns, sit sarkans, sit balts), ko var uzrakstīt vienkārši kā (B, R, B).

5. piemērs Kauliņu mešana. Metlis ir kubs ar sešām malām, no kurām katrā ir viens līdz seši punkti.


Pieņemsim, ka mēs metam kauliņu. Atrast
a) Rezultāti
b) Iznākuma telpa

Risinājums
a) Rezultāti: 1, 2, 3, 4, 5, 6.
b) Iznākuma laukums (1, 2, 3, 4, 5, 6).

Mēs apzīmējam varbūtību, ka notikums E notiek kā P(E). Piemēram, "monēta nolaidīsies uz astes" var apzīmēt ar H. Tad P(H) ir varbūtība, ka monēta nokritīs uz astes. Ja visiem eksperimenta rezultātiem ir vienāda iestāšanās iespējamība, tiek uzskatīts, ka tie ir vienādi iespējami. Lai redzētu atšķirību starp notikumiem, kas ir vienlīdz iespējams, un notikumiem, kas nav vienādi iespējami, apsveriet tālāk norādīto mērķi.

Mērķim A melnā, sarkanā un baltā trāpījuma notikumi ir vienlīdz iespējami, jo melnie, sarkanie un baltie sektori ir vienādi. Tomēr mērķim B zonas ar šīm krāsām nav vienādas, tas ir, trāpīšana tām nav vienlīdz iespējama.

Princips P (teorētiskais)

Ja notikums E var notikt m veidā no n iespējamiem līdzvērtīgiem iznākumiem no iznākuma telpas S, tad teorētiskā varbūtība notikums, P(E) ir
P(E) = m/n.

6. piemērs Kāda ir iespējamība, ka, metot kauliņu, tiks izmests 3?

Risinājums Uz kauliņa ir 6 vienādi iespējamie iznākumi, un ir tikai viena iespēja izmest skaitli 3. Tad varbūtība P būs P(3) = 1/6.

7. piemērs Kāda ir varbūtība, ka uz kauliņa tiks izmests pāra skaitlis?

Risinājums Notikums ir pāra skaitļa mešana. Tas var notikt 3 veidos (ja met 2, 4 vai 6). Līdzvērtīgo iznākumu skaits ir 6. Tad varbūtība P(pāra) = 3/6 jeb 1/2.

Mēs izmantosim vairākus piemērus, kas saistīti ar standarta 52 kāršu komplektu. Šāds klājs sastāv no kārtīm, kas parādītas attēlā zemāk.

8. piemērs Kāda ir iespējamība izvilkt dūzi no labi sajauktas kāršu klāja?

Risinājums Ir 52 iznākumi (kāršu skaits kavā), tie ir vienādi iespējami (ja klājs ir labi sajaukts), un ir 4 veidi, kā izvilkt dūzi, tāpēc pēc P principa, varbūtība
P (dūza vilkšana) = 4/52 vai 1/13.

9. piemērs Pieņemsim, ka mēs, nepaskatoties, izvēlamies vienu bumbiņu no maisa ar 3 sarkanām bumbiņām un 4 zaļām bumbiņām. Kāda ir iespējamība izvēlēties sarkanu bumbiņu?

Risinājums Ir 7 vienādi iespējamie iznākumi jebkuras bumbas iegūšanai, un, tā kā sarkanās bumbiņas izvilkšanas veidu skaits ir 3, mēs iegūstam
P (sarkanās bumbiņas izvēle) = 3/7.

Sekojošie apgalvojumi izriet no P principa.

Varbūtības īpašības

a) Ja notikums E nevar notikt, tad P(E) = 0.
b) Ja notikumam E noteikti jānotiek, tad P(E) = 1.
c) Varbūtība, ka notiks notikums E, ir skaitlis no 0 līdz 1: 0 ≤ P(E) ≤ 1.

Piemēram, metot monētu, gadījumam, ka monēta nokrīt uz tās malas, ir nulle iespējamība. Varbūtība, ka monētai ir galva vai aste, ir 1.

10. piemērs Pieņemsim, ka no klāja, kurā ir 52 kārtis, tiek izvilktas 2 kārtis. Kāda ir varbūtība, ka abi ir pīķi?

Risinājums Veidu skaits n, kā izvilkt 2 kārtis no labi sajaukta 52 kāršu klāja, ir 52 C 2 . Tā kā 13 no 52 kārtīm ir lāpstas, 2 pīķu izvilkšanas veidu skaits m ir 13 C 2 . Tad
P (stiepjas 2 virsotnes) \u003d m / n \u003d 13 C 2 / 52 C 2 \u003d 78/1326 \u003d 1/17.

11. piemērs Pieņemsim, ka no 6 vīriešu un 4 sieviešu grupas nejauši tiek izvēlēti 3 cilvēki. Kāda ir varbūtība, ka tiks izvēlēts 1 vīrietis un 2 sievietes?

Risinājums Veidu skaits, kā izvēlēties trīs cilvēkus no 10 cilvēku grupas 10 C 3 . Vienu vīrieti var izvēlēties 6 C 1 veidos un 2 sievietes var izvēlēties 4 C 2 veidos. Saskaņā ar skaitīšanas pamatprincipu 1. vīrieti un 2 sievietes var izvēlēties 6 C 1 . 4C2. Tad varbūtība, ka tiks izvēlēts 1 vīrietis un 2 sievietes
P = 6 C 1 . 4 C 2 / 10 C 3 \u003d 3/10.

12. piemērs Kauliņu mešana. Kāda ir varbūtība uz diviem kauliņiem kopā uzmest 8?

Risinājums Katram kauliņam ir 6 iespējamie rezultāti. Rezultāti tiek dubultoti, tas ir, ir 6,6 vai 36 iespējamie veidi, kā skaitļi uz diviem kauliņiem var samazināties. (Labāk, ja kubi ir atšķirīgi, teiksim, ka viens ir sarkans, bet otrs zils — tas palīdzēs vizualizēt rezultātu.)

Ciparu pāri, kas kopā veido 8, ir parādīti attēlā zemāk. Ir 5 iespējamie veidi, kā iegūt summu, kas vienāda ar 8, tāpēc varbūtība ir 5/36.

IEVADS

Daudzas lietas mums ir nesaprotamas, nevis tāpēc, ka mūsu jēdzieni ir vāji;
bet tāpēc, ka šīs lietas neietilpst mūsu jēdzienu lokā.
Kozma Prutkova

Matemātikas apguves galvenais mērķis vidējās specializētās izglītības iestādēs ir sniegt studentiem matemātikas zināšanu un prasmju kopumu, kas nepieciešams citu programmas disciplīnu apguvei, kas vienā vai otrā pakāpē izmanto matemātiku, prasmei veikt praktiskus aprēķinus, veidošanai un attīstībai. loģiskā domāšana.

Šajā rakstā ir secīgi ieviesti visi matemātikas sadaļas "Varbūtību teorijas un matemātiskās statistikas pamati" pamatjēdzieni, ko paredz programma un vidējās profesionālās izglītības valsts izglītības standarti (Krievijas Federācijas Izglītības ministrija. M. ., 2002), ir formulētas galvenās teorēmas, no kurām lielākā daļa nav pierādīta. Apskatīti galvenie uzdevumi un to risināšanas metodes un tehnoloģijas šo metožu pielietošanai praktisko problēmu risināšanā. Prezentācijai pievienoti detalizēti komentāri un daudzi piemēri.

Metodiskos norādījumus var izmantot sākotnējai iepazīšanai ar pētāmo materiālu, lekciju pierakstiem, gatavošanos praktiskiem vingrinājumiem, iegūto zināšanu, prasmju un iemaņu nostiprināšanai. Turklāt rokasgrāmata būs noderīga bakalaura studentiem kā atsauces rīks, kas ļauj ātri atjaunot atmiņā iepriekš pētīto.

Darba beigās tiek doti piemēri un uzdevumi, kurus skolēni var veikt paškontroles režīmā.

Metodiskie norādījumi paredzēti neklātienes un pilna laika izglītības formu studentiem.

PAMATJĒDZIENI

Varbūtību teorija pēta masu nejaušu notikumu objektīvās likumsakarības. Tā ir matemātiskās statistikas teorētiskā bāze, kas nodarbojas ar novērojumu rezultātu vākšanas, aprakstīšanas un apstrādes metožu izstrādi. Izmantojot novērojumus (testus, eksperimentus), t.i. pieredze šī vārda plašā nozīmē, ir zināšanas par reālās pasaules parādībām.

Savā praktiskajā darbībā mēs bieži sastopamies ar parādībām, kuru iznākumu nav iespējams paredzēt, kuru rezultāts ir atkarīgs no nejaušības.

Nejaušu parādību var raksturot ar tās sastopamību skaita attiecību pret izmēģinājumu skaitu, no kuriem katrā ar vienādiem visu izmēģinājumu nosacījumiem tā varētu notikt vai nenotikt.

Varbūtību teorija ir matemātikas nozare, kurā tiek pētītas nejaušas parādības (notikumi) un atklājas likumsakarības, kad tās masveidā atkārtojas.

Matemātiskā statistika ir matemātikas nozare, kuras priekšmets ir statistikas datu vākšanas, sistematizācijas, apstrādes un izmantošanas metožu izpēte, lai iegūtu zinātniski pamatotus secinājumus un pieņemtu lēmumus.

Tajā pašā laikā statistikas dati tiek saprasti kā skaitļu kopums, kas atspoguļo mūs interesējošo pētāmo objektu pazīmju kvantitatīvos raksturlielumus. Statistikas dati tiek iegūti speciāli izstrādātu eksperimentu un novērojumu rezultātā.

Statistikas dati savā būtībā ir atkarīgi no daudziem nejaušiem faktoriem, tāpēc matemātiskā statistika ir cieši saistīta ar varbūtību teoriju, kas ir tās teorētiskā bāze.

I. IESPĒJAMĪBA. SADALĪŠANAS UN VARBŪTĪBU REIKINĀŠANAS TEORMAS

1.1. Kombinatorikas pamatjēdzieni

Matemātikas sadaļā, ko sauc par kombinatoriku, tiek risinātas dažas problēmas, kas saistītas ar kopu izskatīšanu un dažādu šo kopu elementu kombināciju sastādīšanu. Piemēram, ja ņemsim 10 dažādus skaitļus 0, 1, 2, 3,:, 9 un izveidosim no tiem kombinācijas, iegūsim dažādus skaitļus, piemēram, 143, 431, 5671, 1207, 43 utt.

Redzam, ka dažas no šīm kombinācijām atšķiras tikai ar ciparu secību (piemēram, 143 un 431), citas ar tajās iekļautajiem cipariem (piemēram, 5671 un 1207), bet citas atšķiras arī ar ciparu skaitu ( piemēram, 143 un 43).

Tādējādi iegūtās kombinācijas atbilst dažādiem nosacījumiem.

Atkarībā no apkopošanas noteikumiem var izdalīt trīs veidu kombinācijas: permutācijas, izvietojumi, kombinācijas.

Vispirms iepazīsimies ar koncepciju faktoriāls.

Tiek izsaukts visu naturālo skaitļu reizinājums no 1 līdz n ieskaitot n-faktoriāls un rakstiet.

Aprēķināt: a) ; b) ; in) .

Risinājums. a) .

b) kā arī , tad varat to izņemt no iekavām

Tad saņemam

iekšā) .

Permutācijas.

n elementu kombināciju, kas atšķiras viens no otra tikai elementu secībā, sauc par permutāciju.

Permutācijas ir apzīmētas ar simbolu P n , kur n ir elementu skaits katrā permutācijā. ( R- franču vārda pirmais burts permutācija- permutācija).

Permutāciju skaitu var aprēķināt, izmantojot formulu

vai ar faktoriālu:

Atcerēsimies to 0!=1 un 1!=1.

Piemērs 2. Cik dažādos veidos vienā plauktā var izkārtot sešas dažādas grāmatas?

Risinājums. Vēlamais veidu skaits ir vienāds ar 6 elementu permutāciju skaitu, t.i.

Naktsmītnes.

Izvietojumi no m elementi iekšā n katrā tiek saukti tādi savienojumi, kas atšķiras viens no otra vai nu ar pašiem elementiem (vismaz vienu), vai pēc secības no atrašanās vietas.

Atrašanās vietas tiek apzīmētas ar simbolu , kur m ir visu pieejamo elementu skaits, n ir elementu skaits katrā kombinācijā. ( BET- franču vārda pirmais burts vienošanās, kas nozīmē "izvietošana, sakārtošana").

Tajā pašā laikā tiek pieņemts, ka nm.

Izvietojumu skaitu var aprēķināt, izmantojot formulu

,

tie. visu iespējamo izvietojumu skaits no m elementi n ir vienāds ar produktu n secīgi veseli skaitļi, no kuriem lielākais ir m.

Mēs rakstām šo formulu faktoriālā formā:

Piemērs 3. Cik daudz iespēju var piešķirt pieciem pretendentiem trīs kuponu sadalei dažāda profila sanatorijai?

Risinājums. Vēlamais opciju skaits ir vienāds ar 5 elementu izvietojumu skaitu pa 3 elementiem, t.i.

.

Kombinācijas.

Kombinācijas ir visas iespējamās kombinācijas m elementi n, kas atšķiras viens no otra vismaz ar vienu elementu (šeit m un n- naturālie skaitļi un n m).

Kombināciju skaits no m elementi n ir apzīmēti ( NO- franču vārda pirmais burts kombinācija- kombinācija).

Kopumā skaits m elementi no n vienāds ar izvietojumu skaitu no m elementi no n dalīts ar permutāciju skaitu no n elementi:

Izmantojot faktoru formulas izvietojuma un permutācijas skaitļiem, mēs iegūstam:

4. piemērs. 25 cilvēku komandā jums ir jāpiešķir četri darbam noteiktā jomā. Cik daudzos veidos to var izdarīt?

Risinājums. Tā kā izvēlēto četru cilvēku secībai nav nozīmes, to var izdarīt dažādos veidos.

Mēs atrodam pēc pirmās formulas

.

Turklāt, risinot problēmas, tiek izmantotas šādas formulas, kas izsaka kombināciju galvenās īpašības:

(pēc definīcijas un tiek pieņemti);

.

1.2. Kombinatorisko uzdevumu risināšana

1. uzdevums. Fakultātē tiek apgūti 16 priekšmeti. Pirmdien grafikā jāieliek 3 priekšmeti. Cik daudzos veidos to var izdarīt?

Risinājums. Ir tikpat daudz veidu, kā ieplānot trīs vienumus no 16, kā arī ir izvietoti 16 elementi pa 3 katrā.

Uzdevums 2. No 15 objektiem jāizvēlas 10 objekti. Cik daudzos veidos to var izdarīt?

Uzdevums 3. Sacensībās piedalījās četras komandas. Cik iespējas ir iespējamas vietu sadales starp tām?

.

4. uzdevums. Cik veidos var izveidot patruļu no trim karavīriem un viena virsnieka, ja tajā ir 80 karavīri un 3 virsnieki?

Risinājums. Var izvēlēties patruļas karavīru

veidus un virsnieku veidus. Tā kā katrs virsnieks var iet ar katru karavīru komandu, ir tikai veidi.

5. uzdevums. Atrodi, vai ir zināms, ka .

Kopš , mēs saņemam

,

,

No kombinācijas definīcijas izriet, ka , . Tas. .

1.3. Nejauši notikuma jēdziens. Pasākumu veidi. Notikuma varbūtība

Tiks izsaukta jebkura darbība, parādība, novērojums ar vairākiem dažādiem rezultātiem, kas realizēts noteiktā nosacījumu kopumā pārbaude.

Šīs darbības vai novērojuma rezultāts tiek saukts notikumu .

Ja notikums noteiktos apstākļos var notikt vai nenotikt, tad to sauc nejauši . Gadījumā, ja notikumam noteikti jānotiek, tas tiek izsaukts autentisks , un gadījumā, ja tas noteikti nevar notikt, - neiespējami.

Pasākumi tiek saukti nesaderīgi ja katru reizi var parādīties tikai viens no tiem.

Pasākumi tiek saukti locītavu ja dotajos apstākļos viena no šiem notikumiem rašanās neizslēdz otra rašanos tajā pašā pārbaudē.

Pasākumi tiek saukti pretī , ja testa apstākļos tie, kas ir vienīgie rezultāti, nav saderīgi.

Notikumi parasti tiek apzīmēti ar latīņu alfabēta lielajiem burtiem: A, B, C, D, : .

Pilnīga notikumu sistēma A 1 , A 2 , A 3 , : , A n ir nesaderīgu notikumu kopums, no kuriem vismaz viena iestāšanās konkrētajam testam ir obligāta.

Ja pilnīga sistēma sastāv no diviem nesaderīgiem notikumiem, tad šādus notikumus sauc par pretējiem un apzīmē ar A un .

Piemērs. Kastītē ir 30 numurētas bumbiņas. Nosakiet, kurš no šiem notikumiem ir neiespējams, noteikts, pretējs:

ieguva numurētu bumbiņu (BET);

uzzīmē pāra numuru bumbiņu (AT);

izvilka bumbiņu ar nepāra skaitli (NO);

ieguva bumbu bez numura (D).

Kuri no viņiem veido pilnīgu grupu?

Risinājums . BET- noteikts notikums; D- neiespējams notikums;

In un NO- pretēji notikumi.

Visa pasākumu grupa ir BET un D, V un NO.

Notikuma varbūtība tiek uzskatīta par nejauša notikuma iestāšanās objektīvās iespējas mēru.

1.4. Klasiskā varbūtības definīcija

Tiek izsaukts skaitlis, kas ir notikuma objektīvās iespējamības mēra izteiksme varbūtība šo notikumu un apzīmē ar simbolu P(A).

Definīcija. Notikuma varbūtība BET ir to iznākumu skaita m attiecība, kas veicina konkrēta notikuma rašanos BET, uz numuru n visi iznākumi (nesaderīgi, unikāli un vienlīdz iespējami), t.i. .

Tāpēc, lai atrastu notikuma iespējamību, pēc dažādu testa rezultātu izvērtēšanas ir jāaprēķina visi iespējamie nesaderīgie rezultāti n, izvēlieties mūs interesējošo rezultātu skaitu m un aprēķiniet attiecību m uz n.

No šīs definīcijas izriet šādas īpašības:

Jebkura izmēģinājuma varbūtība ir nenegatīvs skaitlis, kas nepārsniedz vienu.

Patiešām, vēlamo notikumu skaits m atrodas robežās . Abas daļas sadalot n, saņemam

2. Noteikta notikuma varbūtība ir vienāda ar vienu, jo .

3. Neiespējama notikuma varbūtība ir nulle, jo .

Problēma 1. No 1000 loterijas biļetēm ir 200 laimētāji. Viena biļete tiek izlozēta pēc nejaušības principa. Kāda ir varbūtība, ka šī biļete uzvarēs?

Risinājums. Kopējais dažādu rezultātu skaits ir n=1000. Iznākumu skaits, kas dod priekšroku uzvarai, ir m=200. Pēc formulas iegūstam

.

Uzdevums 2. Partijā, kurā ir 18 daļas, ir 4 bojātas. Pēc nejaušības principa tiek izvēlēti 5 gabali. Atrodiet varbūtību, ka divas no šīm 5 daļām ir bojātas.

Risinājums. Visu vienādi iespējamo neatkarīgo rezultātu skaits n ir vienāds ar kombināciju skaitu no 18 līdz 5 t.i.

Aprēķināsim skaitli m, kas dod priekšroku notikumam A. Starp 5 nejauši izvēlētajām daļām jābūt 3 kvalitatīvām un 2 bojātām. Divu bojātu detaļu izvēles veidu skaits no 4 pieejamajām bojātajām daļām ir vienāds ar kombināciju skaitu no 4 līdz 2:

Veidu skaits, kā izvēlēties trīs kvalitatīvas daļas no 14 pieejamajām kvalitātes daļām, ir vienāds ar

.

Jebkura kvalitatīvu detaļu grupa var tikt kombinēta ar jebkuru bojāto detaļu grupu, tātad kopējais kombināciju skaits m ir

Vēlamā notikuma A varbūtība ir vienāda ar to iznākumu skaita m attiecību, kas ir labvēlīgi šim notikumam, pret visu vienādi iespējamo neatkarīgo iznākumu skaitu n:

.

Noteikta notikumu skaita summa ir notikums, kas sastāv no vismaz viena no tiem iestāšanās.

Divu notikumu summu apzīmē ar simbolu A + B un summu n notikumu simbols A 1 +A 2 + : +A n .

Varbūtību saskaitīšanas teorēma.

Divu nesaderīgu notikumu summas varbūtība ir vienāda ar šo notikumu varbūtību summu.

Secinājums 1. Ja notikums А 1 , А 2 , : , А n veido pilnīgu sistēmu, tad šo notikumu varbūtību summa ir vienāda ar vienu.

Secinājums 2. Pretēju notikumu varbūtību summa un ir vienāda ar vienu.

.

Problēma 1. Ir 100 loterijas biļetes. Ir zināms, ka 5 biļetes iegūst laimestu 20 000 rubļu, 10 - 15 000 rubļu, 15 - 10 000 rubļu, 25 - 2 000 rubļu. un pārējiem nekas. Atrodiet varbūtību, ka iegādātā biļete laimēs vismaz 10 000 rubļu.

Risinājums. Lai A, B un C ir notikumi, kas sastāv no tā, ka uz iegādātās biļetes tiek saņemta balva 20 000, 15 000 un 10 000 rubļu apmērā. tā kā notikumi A, B un C nav savienojami, tad

Uzdevums 2. Tehnikuma neklātienes daļa saņem kontroldarbus matemātikā no pilsētām A, B un NO. Kontroldarbu saņemšanas iespējamība no pilsētas BET vienāds ar 0,6, no pilsētas AT- 0,1. Atrodiet varbūtību, ka nākamie kontroles darbi nāks no pilsētas NO.

Kas ir varbūtība?

Pirmo reizi saskaroties ar šo terminu, es nesaprastu, kas tas ir. Tāpēc mēģināšu izskaidrot saprotamā veidā.

Varbūtība ir iespēja, ka notiks vēlamais notikums.

Piemēram, jūs nolēmāt apmeklēt draugu, atcerieties ieeju un pat grīdu, kurā viņš dzīvo. Bet es aizmirsu dzīvokļa numuru un atrašanās vietu. Un tagad jūs stāvat kāpņu telpā, un jūsu priekšā ir durvis, no kurām izvēlēties.

Kāda ir iespēja (varbūtība), ka, piezvanot pie pirmā durvīm, draugs tās tev atvērs? Viss dzīvoklis, un draugs dzīvo tikai aiz viena. Ar vienādām iespējām mēs varam izvēlēties jebkuras durvis.

Bet kāda ir šī iespēja?

Durvis, labās durvis. Varbūtība uzminēt, zvanot pa pirmajām durvīm: . Tas ir, vienu reizi no trim jūs noteikti uzminēsit.

Vēlamies vienreiz piezvanot uzzināt, cik bieži uzminēsim durvis? Apskatīsim visas iespējas:

1. tu zvanīji 1 Durvis
2. tu zvanīji 2 Durvis
3. tu zvanīji 3 Durvis

Un tagad apsveriet visas iespējas, kur var būt draugs:

a. Per 1 durvis
b. Per 2 durvis
iekšā. Per 3 durvis

Salīdzināsim visas iespējas tabulas veidā. Atzīme norāda opcijas, kad jūsu izvēle atbilst drauga atrašanās vietai, krusts - kad tā neatbilst.

Kā tu visu redzi Var būt iespējas drauga atrašanās vieta un jūsu izvēle, uz kurām durvīm zvanīt.

BET visiem labvēlīgiem rezultātiem . Tas ir, laikus uzminēsi no, vienreiz piezvanot pie durvīm, t.i. .

Tāda ir varbūtība – labvēlīga iznākuma (kad tava izvēle sakrita ar drauga atrašanās vietu) attiecība pret iespējamo notikumu skaitu.

Definīcija ir formula. Varbūtību parasti apzīmē ar p, tāpēc:

Nav īpaši ērti uzrakstīt šādu formulu, tāpēc ņemsim par - labvēlīgo iznākumu skaitu un par - kopējo iznākumu skaitu.

Varbūtību var uzrakstīt procentos, šim nolūkam iegūtais rezultāts jāreizina ar:

Iespējams, jūsu uzmanību piesaistīja vārds “iznākumi”. Tā kā matemātiķi dažādas darbības (mums tāda darbība ir durvju zvans) sauc par eksperimentiem, tad šādu eksperimentu rezultātu pieņemts saukt par iznākumu.

Nu, rezultāti ir labvēlīgi un nelabvēlīgi.

Atgriezīsimies pie mūsu piemēra. Teiksim, mēs piezvanījām pie vienām durvīm, bet mums tās atvēra svešinieks. Mēs neuzminējām. Kāda ir varbūtība, ka, ja mēs piezvanīsim kādām no atlikušajām durvīm, mūsu draugs tās mums atvērs?

Ja jūs tā domājāt, tad tā ir kļūda. Izdomāsim.

Mums ir palikušas divas durvis. Tātad mums ir iespējamie soļi:

1) Zvaniet uz 1 Durvis
2) Zvanīt 2 Durvis

Draugs ar visu šo noteikti ir aiz viena no viņiem (galu galā viņš nebija aiz tā, kuru mēs saucām):

a) draugs 1 durvis
b) draugs par 2 durvis

Uzzīmēsim tabulu vēlreiz:

Kā redzat, visam ir iespējas, no kurām tās ir labvēlīgas. Tas ir, varbūtība ir vienāda.

Kāpēc ne?

Situācija, ko esam apsvēruši, ir atkarīgu notikumu piemērs. Pirmais notikums ir pirmais durvju zvans, otrais notikums ir otrais durvju zvans.

Un tos sauc par atkarīgiem, jo ​​tie ietekmē šādas darbības. Galu galā, ja draugs atvērtu durvis pēc pirmā zvana, kāda būtu varbūtība, ka viņš atrodas aiz kāda no pārējiem diviem? Pareizi,.

Bet, ja ir atkarīgi notikumi, tad jābūt neatkarīgs? Tiesa, tādas ir.

Mācību grāmatas piemērs ir monētas mešana.

1. Mēs metam monētu. Kāda ir varbūtība, ka, piemēram, pacelsies galvas? Tieši tā - jo izvēles iespējas visam (galvas vai astes, mēs neņemsim vērā varbūtību, ka monēta nostāsies uz malas), bet der tikai mums.
2. Bet astes izkrita. Labi, darīsim to vēlreiz. Kāda ir varbūtība, ka tagad uznāks galvas? Nekas nav mainījies, viss ir pa vecam. Cik daudz iespēju? Divas. Cik mēs esam apmierināti? Viens.

Un lai astes izkrīt vismaz tūkstoš reižu pēc kārtas. Varbūtība, ka uzreiz nokritīs galvas, būs vienāda. Vienmēr ir iespējas, bet labvēlīgas.

Ir viegli atšķirt atkarīgos notikumus no neatkarīgiem notikumiem:

1. Ja eksperiments tiek veikts vienu reizi (vienreiz tiek iemesta monēta, vienreiz noskan durvju zvans utt.), tad notikumi vienmēr ir neatkarīgi.
2. Ja eksperimentu veic vairākas reizes (monēta tiek iemesta vienu reizi, durvju zvans tiek piezvanīts vairākas reizes), tad pirmais notikums vienmēr ir neatkarīgs. Un tad, ja mainās labvēlīgo skaits vai visu iznākumu skaits, tad notikumi ir atkarīgi, un, ja nē, tie ir neatkarīgi.

Mazliet trenēsimies, lai noteiktu varbūtību.

1. piemērs

Monēta tiek izmesta divas reizes. Kāda ir varbūtība, ka divas reizes pēc kārtas pacelsies uz augšu?

Risinājums:

Apsveriet visas iespējamās iespējas:

1. ērglis ērglis
2. astes ērglis
3. astes-ērglis
4. Astes-astes

Kā redzat, visas iespējas. No tiem mēs esam apmierināti tikai. Tāda ir varbūtība:

Ja nosacījums prasa vienkārši atrast varbūtību, tad atbilde ir jāsniedz kā decimāldaļdaļa. Ja būtu norādīts, ka atbilde jāsniedz procentos, tad mēs reizinātu ar.

Atbilde:

2. piemērs

Šokolādes kastītē visas konfektes ir iepakotas vienā iesaiņojumā. Toties no saldumiem – ar riekstiem, konjaku, ķiršiem, karameli un nugu.

Kāda ir iespējamība paņemt vienu konfekti un iegūt konfekti ar riekstiem. Norādiet savu atbildi procentos.

Risinājums:

Cik daudz iespējamo rezultātu ir? .

Tas ir, paņemot vienu konfekti, tā būs viena no kastītē esošajām.

Un cik daudz labvēlīgu rezultātu?

Jo kastītē ir tikai šokolādes konfektes ar riekstiem.

Atbilde:

3. piemērs

Bumbiņu kastē. no kuriem ir balts un melns.

1. Kāda ir iespējamība uzzīmēt baltu bumbiņu?
2. Kastei pievienojām vēl melnas bumbiņas. Kāda ir iespējamība uzzīmēt baltu bumbiņu tagad?

Risinājums:

a) Kastē ir tikai bumbiņas. no kuriem ir balti.

Varbūtība ir:

b) Tagad kastē ir bumbiņas. Un balto palikuši tikpat daudz.

Atbilde:

Pilna iespējamība

Visu iespējamo notikumu varbūtība ir ().

Piemēram, sarkano un zaļo bumbiņu kastē. Kāda ir iespējamība uzzīmēt sarkanu bumbiņu? Zaļā bumba? Sarkana vai zaļa bumba?

Sarkanas bumbiņas uzzīmēšanas varbūtība

Zaļā bumba:

Sarkana vai zaļa bumba:

Kā redzat, visu iespējamo notikumu summa ir vienāda ar (). Izpratne par šo punktu palīdzēs atrisināt daudzas problēmas.

4. piemērs

Kastītē ir pildspalvas ar flomāsteriem: zaļa, sarkana, zila, dzeltena, melna.

Kāda ir iespējamība, ka tiks uzzīmēts NAV sarkans marķieris?

Risinājums:

Saskaitīsim skaitli labvēlīgus rezultātus.

NAV sarkans marķieris, tas nozīmē zaļu, zilu, dzeltenu vai melnu.

Visu notikumu iespējamība. Un notikumu iespējamība, ko mēs uzskatām par nelabvēlīgu (kad izvelkam sarkanu flomāsteru) ir .

Tādējādi varbūtība uzzīmēt NAV sarkanu flomāsteru ir -.

Atbilde:

Varbūtība, ka notikums nenotiks, ir mīnus iespējamība, ka notikums notiks.

Neatkarīgu notikumu varbūtību reizināšanas noteikums

Jūs jau zināt, kas ir neatkarīgi notikumi.

Un, ja jums ir jāatrod iespējamība, ka pēc kārtas notiks divi (vai vairāki) neatkarīgi notikumi?

Pieņemsim, ka mēs vēlamies zināt, kāda ir iespējamība, ka, vienu reizi metot monētu, mēs redzēsim ērgli divreiz?

Mēs jau esam apsvēruši - .

Ko darīt, ja mēs iemetam monētu? Kāda ir iespēja ieraudzīt ērgli divas reizes pēc kārtas?

Kopējais iespējamo variantu skaits:

1. Ērglis-ērglis-ērglis
2. Ērglis-galva-astes
3. Galvas-astes-ērglis
4. Galva-astes-astes
5. astes-ērglis-ērglis
6. Astes-galvas-astes
7. Astes-astes-galvas
8. Astes-astes-astes

Es nezinu, kā jums, bet es reiz šo sarakstu izveidoju nepareizi. Oho! Un vienīgais variants (pirmais) mums ir piemērots.

5 ruļļiem varat pats izveidot sarakstu ar iespējamiem rezultātiem. Bet matemātiķi nav tik strādīgi kā jūs.

Tāpēc viņi vispirms pamanīja un pēc tam pierādīja, ka noteiktas neatkarīgu notikumu secības iespējamība katru reizi samazinās par viena notikuma iespējamību.

Citiem vārdiem sakot,

Apsveriet tās pašas, neveiksmīgās monētas piemēru.

Vai ir varbūtība, ka iztiesāšanas laikā jūs uzrunāsit? . Tagad mēs metam monētu.

Kāda ir iespējamība iegūt astes pēc kārtas?

Šis noteikums darbojas ne tikai tad, ja mums tiek lūgts atrast iespējamību, ka viens un tas pats notikums notiks vairākas reizes pēc kārtas.

Ja mēs vēlētos secīgos metienos atrast secību TAILS-EAGLE-TAILS, mēs darītu to pašu.

Varbūtība iegūt astes - , galvas - .

Varbūtība, ka tiks sasniegta secība TAILS-EAGLE-TAILS-TAILS:

To var pārbaudīt pats, izveidojot tabulu.

Noteikums nesaderīgu notikumu varbūtību pievienošanai.

Tāpēc apstājieties! Jauna definīcija.

Izdomāsim. Paņemsim savu nolietoto monētu un apmetīsim to vienreiz.
Iespējamie varianti:

1. Ērglis-ērglis-ērglis
2. Ērglis-galva-astes
3. Galvas-astes-ērglis
4. Galva-astes-astes
5. astes-ērglis-ērglis
6. Astes-galvas-astes
7. Astes-astes-galvas
8. Astes-astes-astes

Tātad šeit ir nesavienojami notikumi, tā ir noteikta, dota notikumu secība. ir nesavienojami notikumi.

Ja vēlamies noteikt, kāda ir divu (vai vairāku) nesavienojamu notikumu iespējamība, tad saskaitām šo notikumu varbūtības.

Jums jāsaprot, ka ērgļa vai astes zaudēšana ir divi neatkarīgi notikumi.

Ja vēlamies noteikt, kāda ir secības (vai jebkuras citas) izkrišanas varbūtība, tad izmantojam varbūtību reizināšanas noteikumu.
Kāda ir iespējamība, ka ar pirmo mešanu dabū galvu un otro un trešo?

Bet, ja mēs vēlamies zināt, kāda ir varbūtība iegūt kādu no vairākām sekvencēm, piemēram, kad galviņas parādās tieši vienu reizi, t.i. opcijas un tad mums jāpievieno šo secību varbūtības.

Kopējās iespējas mums ir piemērotas.

To pašu var iegūt, saskaitot katras secības rašanās varbūtības:

Tādējādi mēs pievienojam varbūtības, ja vēlamies noteikt dažu, nesaderīgu notikumu secību iespējamību.

Ir lielisks noteikums, kas palīdzēs jums neapjukt, kad reizināt un kad pievienot:

Atgriezīsimies pie piemēra, kurā mēs izmetām monētu reizes un vēlamies uzzināt varbūtību, ka galviņas vienreiz ieraudzīsim.
Kas notiks?

Jānokrīt:
(galvas UN astes UN astes) VAI (astes UN astes UN astes) VAI (astes UN astes UN galvas).
Un tā izrādās:

Apskatīsim dažus piemērus.

5. piemērs

Kastītē ir zīmuļi. sarkana, zaļa, oranža un dzeltena un melna. Kāda ir iespēja uzzīmēt sarkanus vai zaļus zīmuļus?

Risinājums:

Kas notiks? Mums ir jāizvelk (sarkans VAI zaļš).

Tagad ir skaidrs, mēs saskaitām šo notikumu varbūtības:

Atbilde:

6. piemērs

Ar kauliņu met divas reizes, kāda ir varbūtība, ka kopā sanāks 8?

Risinājums.

Kā mēs varam iegūt punktus?

(un) vai (un) vai (un) vai (un) vai (un).

Varbūtība izkrist no vienas (jebkuras) sejas ir .

Mēs aprēķinām varbūtību:

Atbilde:

Treniņš.

Es domāju, ka tagad jums ir kļuvis skaidrs, kad jums ir nepieciešams, kā saskaitīt varbūtības, kad tās pievienot un kad tās reizināt. Vai ne? Pavingrosim.

Uzdevumi:

Ņemsim kāršu kavu, kurā kārtis ir lāpstas, sirdis, 13 nūjas un 13 tamburīnas. No līdz katra tērpa dūzim.

1. Kāda ir iespējamība, ka tiks izvilktas nūjas pēc kārtas (mēs ieliekam pirmo izvilkto kārti atpakaļ klājā un sajaucam)?
2. Kāda ir melnās kārts (lāpstas vai nūjas) izvilkšanas iespējamība?
3. Kāda ir varbūtība uzzīmēt attēlu (džeks, dāma, karalis vai dūzis)?
4. Kāda ir iespējamība uzzīmēt divus attēlus pēc kārtas (noņemam no klāja pirmo izvilkto kārti)?
5. Kāda ir iespējamība, ņemot divas kārtis, savākt kombināciju - (Džeks, Dāma vai Karalis) un Dūzis Secībai, kādā kārtis tiks izvilktas, nav nozīmes.

Atbildes:

1. Katras vērtības kāršu komplektā tas nozīmē:
2. Notikumi ir atkarīgi, jo pēc pirmās izvilktās kārtis ir samazinājies kāršu skaits klājā (kā arī “attēlu” skaits). Sākotnēji džeku, dāmu, karaļu un dūžu kopskaits, kas nozīmē varbūtību, ka ar pirmo kārti tiks izvilkts “attēls”:

   Tā kā mēs noņemam pirmo kārti no klāja, tas nozīmē, ka kavā jau ir palikusi kārts, no kuras ir bildes. Varbūtība uzzīmēt attēlu ar otro karti:

   Tā kā mūs interesē situācija, kad no klāja iegūstam: “attēls” UN “attēls”, tad mums ir jāreizina varbūtības:

   Atbilde:

3. Pēc pirmās kārts izvilkšanas kāršu skaits klājā samazināsies, tāpēc mums ir divas iespējas:
   1) Ar pirmo karti izņemam dūzi, otro - džeku, dāmu vai karali
   2) Ar pirmo kārti izņemam džeku, dāmu vai karali, otro - dūzi. (dūzis un (džeks vai dāma, vai karalis)) vai ((džeks vai dāma vai karalis) un dūzis). Neaizmirstiet par kāršu skaita samazināšanu klājā!

Ja visas problēmas varēji atrisināt pats, tad tu esi lielisks puisis! Tagad uzdevumi par varbūtības teoriju eksāmenā noklikšķināsi kā uz riekstiem!

VARBŪTĪBU TEORIJA. VIDĒJAIS LĪMENIS

Apsveriet piemēru. Pieņemsim, ka metam kauliņu. Kas tas par kaulu, vai jūs zināt? Šis ir kuba nosaukums ar cipariem uz virsmām. Cik seju, tik skaitļu: no līdz cik? Pirms tam.

Tāpēc mēs metam kauliņu un vēlamies, lai tas nāktu klajā ar vai. Un mēs izkrītam.

Varbūtības teorijā viņi saka, kas noticis labvēlīgs pasākums(nejaukt ar labo).

Ja izkristu, pasākums arī būtu labvēlīgs. Kopumā var notikt tikai divi labvēlīgi notikumi.

Cik slikto? Tā kā visi iespējamie notikumi, tad nelabvēlīgie no tiem ir notikumi (tas ir, ja izkrīt vai).

Definīcija:

Varbūtība ir labvēlīgo notikumu skaita attiecība pret visu iespējamo notikumu skaitu.. Tas ir, varbūtība parāda, kāda daļa no visiem iespējamiem notikumiem ir labvēlīgi.

Varbūtība ir apzīmēta ar latīņu burtu (acīmredzot, no angļu vārds varbūtība – varbūtība).

Ierasts varbūtību mērīt procentos (skat. tēmas un). Lai to izdarītu, varbūtības vērtība ir jāreizina ar. Kauliņu piemērā varbūtība.

Un procentos: .

Piemēri (izlemiet paši):

1. Kāda ir iespējamība, ka monētas mešana uzkritīs uz galvām? Un kāda ir astes iespējamība?
2. Kāda ir varbūtība, ka, metot kauliņu, parādīsies pāra skaitlis? Un ar ko - nepāra?
3. Vienu, zilu un sarkanu zīmuļu atvilktnē. Mēs nejauši uzzīmējam vienu zīmuli. Kāda ir iespējamība izvilkt vienkāršu?

Risinājumi:

1. Cik daudz iespēju ir? Galvas un astes - tikai divas. Un cik no tiem ir labvēlīgi? Tikai viens ir ērglis. Tātad varbūtība

   Tas pats ar astēm: .

2. Kopējās opcijas: (cik malu ir kubam, tik daudz dažādu iespēju). Labvēlīgie: (tie visi ir pāra skaitļi :).
   Varbūtība. Ar dīvainu, protams, to pašu.
3. Kopā: . Labvēlīgs: . Varbūtība: .

Pilna iespējamība

Visi atvilktnē esošie zīmuļi ir zaļi. Kāda ir iespējamība uzzīmēt sarkanu zīmuli? Nav izredžu: varbūtība (galu galā labvēlīgi notikumi -).

Šādu notikumu sauc par neiespējamu.

Kāda ir varbūtība uzzīmēt zaļu zīmuli? Labvēlīgu notikumu ir tieši tik daudz, cik notikumu kopumā (visi notikumi ir labvēlīgi). Tātad varbūtība ir vai.

Šādu notikumu sauc par noteiktu.

Ja kastē ir zaļi un sarkani zīmuļi, kāda ir iespējamība uzzīmēt zaļu vai sarkanu? Jau atkal. Ņemiet vērā sekojošo: varbūtība uzzīmēt zaļo ir vienāda, un sarkanā ir .

Kopumā šīs varbūtības ir tieši vienādas. Tas ir, visu iespējamo notikumu varbūtību summa ir vienāda ar vai.

Piemērs:

Zīmuļu kastē starp tiem ir zils, sarkans, zaļš, vienkāršs, dzeltens, bet pārējie ir oranži. Kāda ir varbūtība, ka neuzzīmēsiet zaļu krāsu?

Risinājums:

Atcerieties, ka visas varbūtības summējas. Un varbūtība uzzīmēt zaļu ir vienāda. Tas nozīmē, ka varbūtība neuzzīmēt zaļo ir vienāda.

Atcerieties šo triku: Varbūtība, ka notikums nenotiks, ir vienāda ar varbūtību, ka notikums notiks.

Neatkarīgi notikumi un reizināšanas likums

Jūs divreiz apmetat monētu un vēlaties, lai tā abas reizes parādās. Kāda ir tā iespējamība?

Izskatīsim visas iespējamās iespējas un noteiksim, cik to ir:

Ērglis-ērglis, astes-ērglis, ērglis-astes, astes-astes. Kas vēl?

Viss variants. No tiem mums ir piemērots tikai viens: Ērglis-Ērglis. Tātad varbūtība ir vienāda.

Labi. Tagad uzmetīsim monētu. Skaiti pats. Vai notika? (atbilde).

Iespējams, esat pamanījuši, ka, pieskaitot katru nākamo metienu, varbūtība samazinās par koeficientu. Vispārējo noteikumu sauc reizināšanas noteikums:

Neatkarīgu notikumu iespējamības mainās.

Kas ir neatkarīgi notikumi? Viss ir loģiski: tie ir tie, kas nav atkarīgi viens no otra. Piemēram, kad mēs metam monētu vairākas reizes, katru reizi tiek veikts jauns metiens, kura rezultāts nav atkarīgs no visiem iepriekšējiem metieniem. Ar vienādiem panākumiem mēs varam mest divas dažādas monētas vienlaikus.

Vairāk piemēru:

1. Kauliņš tiek izmests divreiz. Kāda ir iespējamība, ka tas parādīsies abas reizes?
2. Monēta tiek izmesta reizes. Kāda ir varbūtība, ka vispirms dabūšu galvu un pēc tam divas reizes astes?
3. Spēlētājs met divus kauliņus. Kāda ir varbūtība, ka uz tiem esošo skaitļu summa būs vienāda?

Atbildes:

1. Notikumi ir neatkarīgi, kas nozīmē, ka darbojas reizināšanas kārtula: .
2. Ērgļa iespējamība ir vienāda. Astes varbūtība arī. Mēs reizinām:
3. 12 var iegūt tikai tad, ja izkrīt divi -ki: .

Nesaderīgi notikumi un pievienošanas noteikums

Nesaderīgi notikumi ir notikumi, kas pilnā mērā papildina viens otru. Kā norāda nosaukums, tie nevar notikt vienlaikus. Piemēram, ja mēs metam monētu, var izkrist vai nu galvas, vai astes.

Piemērs.

Zīmuļu kastē starp tiem ir zils, sarkans, zaļš, vienkāršs, dzeltens, bet pārējie ir oranži. Kāda ir varbūtība uzzīmēt zaļu vai sarkanu?

Risinājums.

Zaļā zīmuļa uzzīmēšanas varbūtība ir vienāda. Sarkans - .

Visiem labvēlīgi notikumi: zaļš + sarkans. Tātad varbūtība uzzīmēt zaļu vai sarkanu ir vienāda.

To pašu varbūtību var attēlot šādā formā: .

Šis ir pievienošanas noteikums: nesaderīgu notikumu varbūtības summējas.

Jaukti uzdevumi

Piemērs.

Monēta tiek izmesta divas reizes. Kāda ir iespējamība, ka ruļļu rezultāts būs atšķirīgs?

Risinājums.

Tas nozīmē, ka, ja galvas parādās pirmās, astēm jābūt otrajām un otrādi. Izrādās, ka šeit ir divi neatkarīgu notikumu pāri, un šie pāri nav savienojami viens ar otru. Kā neapjukt, kur pavairot un kur pievienot.

Šādām situācijām ir vienkāršs noteikums. Mēģiniet aprakstīt, kam vajadzētu notikt, saistot notikumus ar arodbiedrībām "UN" vai "OR". Piemēram, šajā gadījumā:

Jāripo (galvas un astes) vai (astes un galvas).

Ja ir savienība "un", būs reizināšana, un kur "vai" ir saskaitīšana:

Izmēģiniet to pats:

1. Kāda ir iespējamība, ka divi monētas metieni abas reizes parādīs vienu un to pašu pusi?
2. Kauliņš tiek izmests divreiz. Kāda ir varbūtība, ka summa samazinās punktus?

Risinājumi:

1. (Galvas uz augšu un galvu uz augšu) vai (astes uz augšu un astes uz augšu): .
2. Kādas ir iespējas? un. Pēc tam:
   Velmēti (un) vai (un) vai (un): .

Vēl viens piemērs:

Mēs vienu reizi metam monētu. Kāda ir iespējamība, ka galvas pacelsies vismaz vienu reizi?

Risinājums:

Ak, kā es negribu šķirot iespējas ... Galvas-astes-astes, Ērglis-galvas-astes, ... Bet jums tas nav jādara! Parunāsim par pilnu varbūtību. Atcerējās? Kāda ir varbūtība, ka ērglis nekad nenokritīs? Tas ir vienkārši: astes lido visu laiku, tas nozīmē.

VARBŪTĪBU TEORIJA. ĪSUMĀ PAR GALVENO

Varbūtība ir labvēlīgo notikumu skaita attiecība pret visu iespējamo notikumu skaitu.

Neatkarīgi pasākumi

Divi notikumi ir neatkarīgi, ja viena iestāšanās nemaina otra iestāšanās iespējamību.

Pilna iespējamība

Visu iespējamo notikumu varbūtība ir ().

Varbūtība, ka notikums nenotiks, ir mīnus iespējamība, ka notikums notiks.

Neatkarīgu notikumu varbūtību reizināšanas noteikums

Noteiktas neatkarīgu notikumu secības iespējamība ir vienāda ar katra notikuma varbūtību reizinājumu

Nesaderīgi notikumi

Nesaderīgi notikumi ir notikumi, kas nevar notikt vienlaicīgi eksperimenta rezultātā. Vairāki nesaderīgi notikumi veido pilnīgu notikumu grupu.

Nesaderīgu notikumu iespējamības summējas.

Aprakstot, kam jānotiek, izmantojot savienības "UN" vai "OR", "UN" vietā ievietojam reizināšanas zīmi, bet "OR" vietā - saskaitīšanu.

PĀRĒJIE 2/3 RAKSTI IR PIEEJAMI TIKAI YOUCLEVER STUDENTIEM!

Kļūsti par YouClever studentu,

Sagatavojieties OGE vai izmantojiet matemātikā par cenu "tase kafijas mēnesī",

Un arī iegūstiet neierobežotu piekļuvi mācību grāmatai "YouClever", sagatavošanas programmai "100gia" (rechebnik) izmēģinājuma eksāmens un OGE, 6000 uzdevumu ar risinājumu analīzi un citiem YouClever un 100gia pakalpojumiem.