Matematika në natyrë: shembuj. Matematika në natyrë, numerologjia në jetë Koncepti i harmonisë

19.04.2024 | Letërsia

Koncepti i harmonisë. Ligjet matematikore të përbërjes

Bazat e kompozimit në grafikën e aplikuar

Edhe në kohët e lashta, njeriu zbuloi se të gjitha fenomenet në natyrë janë të lidhura me njëra-tjetrën, se gjithçka është në lëvizje të vazhdueshme, ndryshim dhe, kur shprehet në numra, zbulon modele të mahnitshme.

Në Greqinë e lashtë të epokës klasike, u ngritën një sërë mësimesh për harmoninë. Prej tyre, mësimi i Pitagorës la gjurmën më të thellë në kulturën botërore. Pasuesit e Pitagorës e imagjinonin botën, universin, hapësirën, natyrën dhe njeriun si një tërësi të vetme, ku gjithçka është e ndërlidhur dhe në marrëdhënie harmonike. Harmonia këtu vepron si fillimi i rendit - renditja e kaosit. Harmonia është e natyrshme në natyrë dhe art: " Të njëjtat ligje ekzistojnë për mënyrat muzikore dhe planetët". Pitagorianët dhe pasuesit e tyre po kërkonin një shprehje numerike për gjithçka në botë. Ata zbuluan se përmasat matematikore qëndrojnë në themel të muzikës (raporti i gjatësisë së telit me lartësinë, marrëdhënia midis intervaleve, raporti i tingujve në korda Pitagorianët u përpoqën matematikisht të vërtetonin idenë e unitetit të botës, ata argumentuan se baza e universit ishte forma gjeometrike simetrike përmasat e trupit të njeriut dhe miratoi kanunin matematikor të bukurisë, sipas të cilit skulptori Polykleitos krijoi statujën "Canon".

I gjithë arti klasik i Greqisë mban vulën e doktrinës pitagoriane të përmasave. Ndikimi i tij u përjetua nga shkencëtarët e mesjetës, shkencës dhe artit të Rilindjes, kohët moderne, deri në ditët e sotme. Pas pitagorianëve, shkencëtari mesjetar Agustini e quajti bukurinë "barazi numerike". Filozofi skolastik Bonaventure shkroi: "Nuk ka bukuri dhe kënaqësi pa proporcionalitet, dhe proporcionaliteti ekziston kryesisht në numra." Leonardo da Vinci shkroi për përdorimin e proporcionit në art në traktatin e tij mbi pikturën: " Piktori mishëron në formën e proporcionit të njëjtat modele të fshehura në natyrë që shkencëtari njeh në formën e ligjit numerik.".

Pra, proporcionaliteti, proporcionaliteti i pjesëve të së tërës është kushti më i rëndësishëm për harmoninë e së tërës dhe mund të shprehet matematikisht përmes përmasave.

Proporcioni nënkupton barazinë e dy ose më shumë raporteve. Ekzistojnë disa lloje të proporcionalitetit:

matematikore,
harmonike,
gjeometrike etj.

Në matematikë, barazia e dy marrëdhënieve shprehet me formulën a:b=с:d, dhe secili anëtar i tij mund të përcaktohet përmes tre të tjerëve. Ka 3 elementë në përpjesëtim harmonik. Ato janë ose dallime në çift të disa trefishtë elementësh, ose vetë këta elementë, për shembull:

a:c=(a - c): (c - c)

Në proporcion gjeometrik ka edhe vetëm 3 elementë, por njëri prej tyre është i zakonshëm, a:b=c:c. Një lloj proporcioni gjeometrik është proporcioni i të ashtuquajturës " raporti i artë"Ka vetëm dy anëtarë -" A"Dhe" V"është një proporcion i preferuar i artistëve, i cili në Rilindje quhej "proporcioni hyjnor".

Raporti i artë (g.s.)

E veçanta e proporcionit të seksionit të artë është se termi i fundit në të është ndryshimi midis dy termave të mëparshëm, d.m.th.

a:b=c: (a -c)

Qëndrimi h. Me. shprehur si numër 0,618 .
Përpjesëtimi z. Me. 1:0,618=0,618:0,382 .

Nëse shprehni një segment të drejtëz në terma një, dhe pastaj e ndani atë në dy segmente në z. s., atëherë segmenti më i madh do të jetë i barabartë me 0.618, dhe segmenti më i vogël do të jetë 0.382.

Fig 2. Ndarja e një segmenti sipas raportit të artë

Në bazë të proporcionit h. Me. u ndërtua një seri numrash, domethënëse në atë që çdo numër i mëpasshëm doli të ishte i barabartë me shumën e dy të mëparshmëve: 1, 1, 2, 3, 5, 8, 13, 21, etj. Kjo seri u zbulua nga matematikani italian Fibonacci dhe prandaj quhet seria Fibonacci. Ajo ka vetinë që marrëdhëniet ndërmjet termave fqinjë, me rritjen e numrave të serisë, bëhen gjithnjë e më afër O, b18, pra me raportin 3. Me.

Proporcionet h. Me. shkencëtarët lidhen me zhvillimin e lëndës organike. h. Me. Ai u zbulua në objektet e natyrës së gjallë - në strukturën e guaskave, drurit, në rregullimin e farave të lulediellit, në strukturën e trupit të njeriut, dhe u vërejt gjithashtu në strukturën e universit në rregullimin e planetëve.

Në lidhje me s. Me. Ka edhe elementë të formave gjeometrike - një pesëkëndësh, një yll.

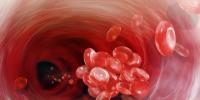
Në drejtkëndëshin h. Me. palët janë në lidhje me s.s. Ky drejtkëndësh përmban një katror dhe një drejtkëndësh të vogël h. Me. (faqja e madhe e tij është ana e vogël e drejtkëndëshit origjinal.) Prandaj, është e mundur të ndërtohet një pr-k z.s. në bazë të një katrori: brinja e katrorit ndahet përgjysmë, nga ajo pikë deri në majë vizatohet një diagonale, me ndihmën e së cilës ndërtohet një pr-k z.s.

Pikat e kryqëzimit të vijave që përbëjnë yllin i ndajnë ato në segmente në raport me raportin e artë. Ky drejtkëndësh i vogël është i ngjashëm me një drejtkëndësh të madh të përbërë nga një katror dhe një drejtkëndësh i vogël h. s., domethënë të dy këta drejtkëndësha janë drejtkëndësha h. Me.

Me fjalë të tjera, nëse e shkëputni z nga drejtkëndëshi. c.. katror, atëherë mbetet një drejtkëndësh më i vogël, brinjët e të cilit përsëri do të jenë në raportin z. Me. Duke e ndarë këtë drejtkëndësh më të vogël në një katror dhe një drejtkëndësh edhe më të vogël, ne përsëri marrim drejtkëndëshin 3. s., e kështu me radhë ad infinitum. Nëse lidhim kulmet e katrorëve të një kurbë, do të marrim një kurbë logaritmike, një spirale pafundësisht në rritje, e cila quhet "kurba e zhvillimit", "spiralja e jetës", sepse duket se përmban idenë e zhvillim të pafund.

Oriz. 4. Drejtkëndësh afërsisht me raport të artë, i ndërtuar mbi bazën e një pesëkëndëshi

Fig. 5. Ndërtimi i një drejtkëndëshi me raport të artë bazuar në një katror.

Përsëritje pa fund h. Me. dhe një katror kur zbërthehet një drejtkëndësh h. Me. zbulon përsëritjen e së tërës në pjesët e saj, që është një nga kushtet për harmoninë e së tërës. Kjo është veti e drejtkëndëshit g.s. u zbulua nga artistët dhe ata filluan të përdorin s. Me. si mënyrë harmonizimi, mënyrë përpjestimi. Phidias përdori z. Me. gjatë ndërtimit të Akropolit (shek. V para Krishtit)

Oriz. 6. Kurba logaritmike "Spiral i Jetës"

Oriz. 7. Ndërtimi i një letre nga libri i Luca Pacioli "Mbi proporcionin hyjnor"

Artizanët grekë përdorën gjithashtu squfur kur krijonin qeramikë. Me. Gjatë Rilindjes h. Me. përdoret jo vetëm në arkitekturë, skulpturë, pikturë, por edhe në poezi dhe muzikë. Dürer, Leonardo da Vinci dhe studenti i tij Luca Pacioli përdorën s. Me. në kërkim të përmasave harmonike të shkronjave. Drejtkëndëshi h. Me. gjejmë si në përmasat e librave të dorëshkrimit mesjetar ashtu edhe në librat modernë, pasi përmasat e holla të h. Me. ju lejon të organizoni bukur hapësirën e një faqe libri dhe të përhapni.

Oriz. 8. Skema e përmasave ideale të një dorëshkrimi mesjetar.

Përmasat e faqes janë 2:3, dhe rrafshi i zënë nga shkronja është në proporcionin e raportit të artë.

Oriz. 9. Një nga mënyrat për të përcaktuar madhësinë e një shiriti shtypjeje për një format të caktuar.

Proporcioni është sjellja e pjesëve të një tërësie në një rend të vetëm proporcional.

Në shekullin e njëzetë, pati një interes të ri për raportin e artë si një metodë përpjestimi.

Tërhoqi vëmendjen e arkitektëve. Arkitekti sovjetik Zholtovsky dhe francezi Corbusier u morën me problemet e kanalizimeve. Me. dhe e përdori atë në praktikën e tyre arkitekturore, Corbusier krijoi një sistem të tërë proporcionaliteti bazuar në numrat e serisë së raportit të artë dhe proporcionet e trupit të njeriut dhe e quajti atë "Modulor", që në latinisht do të thotë "masë ritmikisht".

Oriz. 9. Modulor (diagram i thjeshtuar)

Oriz. 10. Opsione për ndarjen e një drejtkëndëshi bazuar në Modulor.

Moduli i Corbusier përfaqëson seritë harmonike të numrave që janë të lidhur në një sistem të vetëm dhe janë të destinuara për përdorim në arkitekturë dhe dizajn - për të harmonizuar të gjithë mjedisin në të cilin jeton një person. Corbusier ëndërronte të ristrukturonte të gjithë mjedisin arkitekturor dhe objektor me ndihmën e Modulor. Ai vetë krijoi disa shembuj të shkëlqyer të arkitekturës, por një aplikim më i gjerë i Modulor në kushtet ekzistuese nuk bëhej fjalë.

Modulor është përdorur në një sërë mënyrash në dizajn dhe në dizajn grafik - në hartimin e botimeve të shtypura. Në Fig. Figura 16 tregon opsionet për ndarjen e një drejtkëndëshi 3:4, të dhëna nga Corbusier për të demonstruar aftësitë e projektimit duke përdorur Modulor.

D. Hambridge kontribuoi në zhvillimin e çështjes së përpjestimit dhe përdorimit të seksionit të artë. Në vitin 1920, libri i tij "Elementet e simetrisë dinamike" u botua në Nju Jork. Hambidge eksploroi simetrinë dinamike që zbuloi në një seri drejtkëndëshash, me synimin për zbatimin e saj praktik nga artistët në ndërtimin kompozicional. Ai bën një përpjekje për të zbuluar sekretet që grekët e lashtë përdornin për të arritur një zgjidhje harmonike të formës. Vëmendjen e tij e tërhoqën vetitë e drejtkëndëshave që përbëjnë një rresht, ku çdo drejtkëndësh i mëpasshëm ndërtohet mbi diagonalen e të mëparshmit, duke filluar me diagonalen e katrorit C2. Këta janë drejtkëndësha C4, C5 (me anën më të vogël të barabartë me anën e katrorit, marrë si një). (Fig. 17). Kulmi i serisë është drejtkëndëshi T5, i cili ka veti të veçanta harmonike dhe është "i lidhur" me drejtkëndëshin e seksionit të artë (do të diskutohet më poshtë).

Oriz. 11. Një seri drejtkëndëshash dinamikë Hambidge.

Hambidge merr në konsideratë edhe sipërfaqet e katrorëve të ndërtuar në faqet e këtyre drejtkëndëshave dhe zbulon dinamikën e mëposhtme: në ushtrimin C2, një katror i ndërtuar në faqen më të madhe ka një sipërfaqe 2 herë më të madhe se katrori i ndërtuar në faqen më të vogël. Në ushtrimin C3, katrori në anën më të madhe është 3 herë më i madh se katrori në anën më të vogël etj. Në këtë mënyrë formohen seri dinamike zonash, të përbëra nga numra të plotë.

Hambridge argumenton se grekët e lashtë e përdornin këtë parim në vendimet e tyre kompozicionale. Drejtkëndëshat e serive kohore për të cilat folëm janë zonat kryesore në sistemin kompozicional të Hambidge. Secili prej këtyre drejtkëndëshave mund të ndahet në pjesë të veçanta dhe të gjenerojë zgjidhje të reja kompozicionale dhe tema të reja. Për shembull, drejtkëndëshi C5 mund të ndahet në një katror dhe dy drejtkëndësha të raportit të artë. Drejtkëndëshi i raportit të artë mund të ndahet në një drejtkëndësh katror dhe një drejtkëndësh me raport të artë, dhe gjithashtu mund të ndahet në pjesë të barabarta, dhe zbulohet modeli i mëposhtëm: kur ndahet në gjysmë, do të japë dy drejtkëndësha, secili prej të cilëve do të ketë dy të artë raport drejtkëndësha. Kur ndahet në tre pjesë, ka tre drejtkëndësha me raport të artë në çdo të tretën. Kur ndahet në 4 pjesë - katër drejtkëndësha h. Me. në çdo të katërtën e drejtkëndëshit kryesor.

Ndër sistemet proporcionale të përdorura në arkitekturë, dizajn dhe grafikë të aplikuar, duhet të përmenden sistemet e "numrave të preferuar" dhe sistemet e ndryshme modulare.

"Numrat e preferuar" - një seri numrash të një progresion gjeometrik, ku çdo numër pasues formohet duke shumëzuar numrin e mëparshëm me një vlerë konstante. Numrat nga seria e preferuar përdoren në hartimin e paketimit, në përbërjen e posterave reklamues. Ato sigurojnë zhvillimi ritmik i formës mund të gjenden edhe në ndërtimin e vazove të formave të lashta dhe në një makinë moderne.

Një sistem i njohur proporcionaliteti është i ashtuquajturi " Rendit italiane", të cilët bazohen në numrat e parë të serisë Fibonacci - 2, 3, 5. Secili prej këtyre numrave, duke u dyfishuar, formon një seri numrash të lidhur në mënyrë harmonike me njëri-tjetrin:

2 - 4, 8, 16, 32, 64, etj.
3 - 6, 12, 24 48, 96
5 - 10, 20, 40, 80, 160

Përpjestimi lidhet me konceptet proporcionaliteti Dhe masat. Një nga mënyrat për të matur të tërën dhe pjesët e saj është moduli. Moduli- një madhësi ose element që përsëritet në mënyrë të përsëritur në tërësinë dhe pjesët e saj. Moduli(latinisht) do të thotë masë. Çdo masë e gjatësisë mund të jetë një modul. Gjatë ndërtimit të tempujve grekë, u përdor edhe një modul për të arritur proporcionalitetin. Moduli mund të jetë rrezja ose diametri i kolonës, distanca midis kolonave.

Vitruvius, arkitekt romak i shekullit I. para Krishtit e., në traktatin e tij mbi arkitekturën, ai shkroi se proporcioni është korrespondenca midis anëtarëve të të gjithë veprës dhe të tërës së saj - në lidhje me pjesën e marrë si origjinale, mbi të cilën bazohet gjithë proporcionaliteti, dhe proporcionaliteti është harmonia e rreptë. të pjesëve individuale të vetë strukturës dhe korrespondencës së pjesëve individuale dhe të tërës së një pjese specifike, marrë si origjinale.

Në grafikën e aplikuar, moduli përdoret gjerësisht në hartimin e librave, revistave, gazetave, katalogëve, prospekteve dhe të gjitha llojeve të botimeve të shtypura. Përdorimi i rrjetave modulare ndihmon në organizimin e renditjes së teksteve dhe ilustrimeve dhe kontribuon në krijimin e unitetit kompozicional. Dizajni modular i botimeve të printuara bazohet në një kombinim të vijave vertikale dhe horizontale që formojnë një rrjet, duke e ndarë fletën (faqen) në drejtkëndësha të krijuar për të shpërndarë tekstin, ilustrimet dhe hapësirat ndërmjet tyre. Ky modul drejtkëndor (mund të ketë disa prej tyre) përcakton shpërndarjen e organizuar në mënyrë ritmike të materialit në botimin e shtypur.

Ka rrjete të modeleve dhe shkallëve të ndryshme të kompleksitetit. A. Hurlbert jep shembuj të rrjetave modulare për revista, libra dhe gazeta në librin e tij "Rrjeti".

Rrjeti modular nuk duhet të ngatërrohet me rrjetin tipografik, i cili përcakton madhësinë e fushave dhe formatin e faqes së shtypjes. Natyrisht, rrjeti modular, për aq sa ka të bëjë me botimet e shtypura, duhet të marrë parasysh madhësitë e rreshtave, lartësinë e shkronjave dhe elementët e hapësirës së bardhë në masat tipografike (katrore, ciceros, pika) në mënyrë që të pozicionohet saktë materiali i printuar. në faqe.

Sistemi i rrjetit, falë bazës së tij të qartë modulare, ju lejon të futni programe elektronike në procesin e projektimit të publikimit. Në grafikën e aplikuar, industriale, një rrjet modular përdoret në hartimin e të gjitha llojeve të botimeve reklamuese dhe, në veçanti, në hartimin e një stili grafik të korporatës. Rrjeti modular përdoret në projektimin e shenjave të ndryshme, shenjave të komunikimit vizual, markave tregtare, etj.

Oriz. 14. Marka tregtare e ndërtuar mbi bazën e një rrjeti modular.

Oriz. 15. Shenja e komunikimit për Lojërat Olimpike në Mynih. ndërtuar mbi një rrjet modular

Rrjetet modulare shpesh bazohen në një katror. Sheshi është një modul shumë i përshtatshëm. Përdoret gjerësisht si modul në industrinë moderne të mobiljeve, veçanërisht në ndërtimin e mobiljeve të parafabrikuara, "mureve".

Sheshi i dyfishtë është njohur prej kohësh si një modul i shtëpisë tradicionale japoneze, ku përmasat e dhomave ishin në përputhje me sa herë do të shtrohej në dysheme një rrogoz tatami me përmasat e një katrori të dyfishtë.

Në grafikën e aplikuar, katrori përdoret për formatet e prospekteve të albumeve dhe librave për fëmijë, por përcakton edhe hapësirën e brendshme të këtyre botimeve. Moduli katror mund të përdoret gjithashtu në një format jo katror.

Le të japim një shembull të përdorimit të një moduli katror në një format katror: me shtypjen e tekstit me tre kolona, e gjithë zona e caktuar për tekst dhe ilustrime ndahet në 9 katrorë. Nëse gjerësia e kolonës përcaktohet si 1, atëherë katrori do të jetë 1x1. Në këtë rast, ilustrimet mund të zënë zona: 1x1, 1x2, 1x3, 2x2, 2x3, 3x3, 2x1, etj., domethënë do të kemi mundësi mjaft të gjera për kombinimin e ilustrimeve dhe tekstit në paraqitje. Në strukturën kompozicionale të veprave të artit dhe dizajnit, përmasat e drejtkëndëshave dhe formave të tjera gjeometrike në të cilat përshtatet një vepër e caktuar ose pjesët kryesore të saj janë të rëndësishme. Prandaj, duhet të konsiderojmë drejtkëndëshat, të cilët përdoren më gjerësisht për shkak të vetive të tyre harmonike (drejtkëndëshi i raportit të artë u diskutua më lart). Le të shohim sërish sheshin. Sheshi si formë strukturore njihet prej kohësh. Ai tërhoqi vëmendjen e artistëve të Botës së Lashtë dhe të Rilindjes.

Vizatimi nga Leonardo da Vinci përshkruan lidhjen midis një katrori dhe një rrethi me figurën njerëzore, të njohur nga të lashtët (Vitruvius). Artistët e Rilindjes - gjermani Durer, italiani Pacioli, francezi Tory, kur zhvillonin skicën e shkronjave, dolën nga forma e një katrori, shkronja me të gjithë elementët e saj përshtatej në katror (Fig. 12), megjithëse jo të gjitha shkronjat. barazoheshin me një katror, megjithatë, struktura e përgjithshme kompozicionale u përcaktua katror. Një katror është një figurë e qëndrueshme, statike. Ajo shoqërohet me diçka të palëvizshme, të plotë. Në botën e lashtë, midis disa popujve, imazhi i një sheshi shoqërohej me simbolikën e vdekjes. (Në këtë drejtim, është interesante të theksohet se përmasat katrore gjenden në natyrë në forma të lëndës së pajetë, në kristale). Për shkak të plotësisë statike, katrori përdoret në grafikën e aplikuar, në fushën e komunikimeve vizuale, së bashku me formën e një rrethi, si një element që tërheq vëmendjen, si dhe për të kufizuar hapësirën në të cilën përqendrohet informacioni.

Përveç raportit të artë drejtkëndësh dhe katror, drejtkëndëshat Ts2 dhe Ts5 janë me interes më të madh për ne. Grekët e lashtë të epokës klasike preferonin këto drejtkëndësha, Hambidge pretendon se 85% e veprave të artit klasik grek ishin ndërtuar në sheshin C5. Çfarë është interesante për këtë drejtkëndësh? Duke u ndarë vertikalisht dhe horizontalisht në dy pjesë, ajo rikthen përmasat e saj. Ky drejtkëndësh mund të ndahet në një katror dhe dy drejtkëndësha të vegjël të raportit të artë. Për më tepër, ai tregon dy drejtkëndësha të raportit të artë, që mbivendosen me njëra-tjetrën me madhësinë e një katrori. Pjesa e mbetur është gjithashtu një drejtkëndësh i raportit të artë. Kështu, drejtkëndëshi C5 shfaq veti ritmike. Në të shfaqet një simetri e bukur (drejtkëndësh i vogël g.s. + katror + drejtkëndësh i vogël g.s.).

Oriz. 16. Vetitë ritmike të një drejtkëndëshi

Hambidge jep një diagram kompozicional të një filxhani të pijes greke nga Muzeu i Bostonit: kupa përshtatet (pa doreza) në një drejtkëndësh të zgjatur horizontalisht C5 Diagonalet e dy drejtkëndëshave me raport të artë, që mbivendosen në një katror, kryqëzohen në pikën përmes së cilës. kufiri midis kupës dhe këmbës së tij kalon. Gjerësia e bazës së këmbës është e barabartë me lartësinë e tasit dhe e barabartë me faqen e katrorit që ndodhet në qendër të drejtkëndëshit C5. Këmba përshtatet në dy drejtkëndësha të vegjël h. s., i prerë nga katrori me një vijë horizontale në bazën e pr-ka Ts5 dhe që kalon në pikën e kryqëzimit të dy diagonaleve të drejtkëndëshave të mëdhenj h. Me. Në dizajnin modern artistik, drejtkëndëshi Ts5 përdoret gjithashtu gjerësisht. E gjejmë në përmasat e makinave, veglave të makinerive dhe produkteve të tjera. Në grafikë të aplikuar - në formatet e prospekteve, broshurave, paketimit; në artin figurativ, në artin monumental, në përmasat e rrafshit të figurës, në strukturën kompozicionale të figurës.

Drejtkëndëshi Ts2 përdoret gjithashtu gjerësisht, veçanërisht në fushën e grafikës së aplikuar. Përdoret si një format letre për dokumentet e biznesit, sepse ka një veti të mahnitshme - kur ndahet në gjysmë, nuk ndryshon përmasat e tij. Kur ndahen, formohen një numër drejtkëndëshash të ngjashëm, të ndërlidhur në mënyrë harmonike nga uniteti i formës. Në Fig. Figura 18 tregon një imazh të drejtkëndëshave të përdorur në ndërtimin kompozicional për shkak të marrëdhënieve harmonike të anëve të tyre.

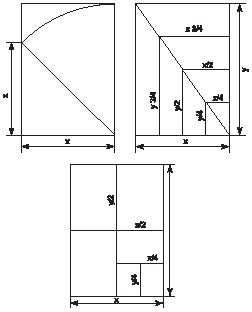
Oriz. 17. Përqindjet e anëve në pr-ke Ts2, të përdorura në standardin Poratman.

Oriz. 18. Marrëdhëniet harmonike të brinjëve në drejtkëndësha.

Më poshtë janë raportet numerike të pr-kov Ts2, Ts3, Ts4, Ts5 me numrat e tyre reciprokë me të cilët janë në një marrëdhënie harmonike. (Reciprociteti i një numri është numri i marrë duke pjesëtuar një me një numër të caktuar.) Nëse e marrim anën më të vogël të drejtkëndëshit si një, atëherë për drejtkëndëshin numri (që i përgjigjet brinjës më të madhe të drejtkëndëshit) = 1,4142, dhe numri reciprok = 0,7071; për pr-ka numri Ts3 = 1,732, numri reciprok = 0,5773; për pr-ka numri Ts4 = 2, numri reciprok = 0,5; për pr-ka numrin Ts5 = 2.236; reciproke=0,4472; për pr-ka" z.s. numri = 1.618, numri reciprok = 0.618.

Bazuar në projektin Ts2, u krye standardizimi dhe unifikimi i formateve të librave, letrave, dokumenteve të biznesit, kartolinave, posterave, dosjeve dhe objekteve të tjera që lidhen me grafikën e aplikuar. Ky standard, i njohur si standardi Dr. Porstmann, është miratuar në 17 vende evropiane. Standardi bazohej në një format prej 841X1189 mm dhe një sipërfaqe prej 1 m 2. Pjesa tjetër e formateve që përbëjnë aksionet e saj rrjedhin prej saj:

1m 2 - 841 X 1189 mm
1/2m 2 - 594 Х841mm
1/4 m 2 - 420 X 594 mm
1/8 m 2 - 297Х420 mm (fletë e dyfishtë)
1/16m 2 - 210Х 297mm (fletë për korrespondencë biznesi, formularë)
1/32m 2 - 148Х210mm (gjysmë fletë për korrespondencë biznesi, formularë)
1/64m 2 - 105Х148mm (kartolinë)
1/128 m 2 - 74X105 mm (kartë biznesi)

Standardi parashikon gjithashtu formate shtesë 1000X1414 dhe 917X1297 dhe aksionet e tyre. Përmasat e disponueshme për zarfe janë: 162X229 dhe 114X162. (Standardi nuk është dhënë i plotë).

Oriz. 19. Ndarja e një drejtkëndëshi në pjesë: 1/2, 1/4, 1/8, 1/16,1/64.

Meqenëse trajtimi i letrave dhe dokumentacionit të biznesit nënkupton nevojën për të pasur jo vetëm zarfe dhe dosje që përputhen me madhësinë dhe formatin e tyre, por edhe kontejnerë në të cilët ruhet dokumentacioni, prandaj nevoja për mobilje të përshtatshme: tavolina, dollapë, rafte. Përmasat dhe përmasat e mobiljeve, nga ana tjetër, sugjerojnë karakterin e ambienteve të brendshme të ambienteve. Kështu, shfaqet një sistem i plotë i elementeve të brendshme të harmonizuara, të varura nga një parim i vetëm modular.

Marrëdhëniet proporcionale duhet të ekzistojnë jo vetëm midis pjesëve individuale të së tërës, por edhe midis objekteve që përbëjnë grupe objektesh të lidhura me një stil të vetëm dhe detyrë funksionale. Për shembull, midis objekteve të përfshira në sistemin e identitetit të korporatës.

Objektet që rrethojnë një person duhet të harmonizohen jo vetëm në raport me njëri-tjetrin, por edhe të lidhen me një person në një masë të vetme, me strukturën e tij fizike. Arkitektët e antikitetit besonin se marrëdhënia e pjesëve të arkitekturës me njëra-tjetrën dhe me tërësinë duhet të korrespondojë me pjesët e trupit të njeriut dhe marrëdhëniet e tyre. Në të njëjtën mënyrë, Modulor i Corbusier rrjedh nga dimensionet e trupit të njeriut dhe nga marrëdhëniet e seksionit të artë në të (distanca nga toka në plexusin diellor dhe distanca nga pleksusi diellor në kurorë përbëjnë ekstremin dhe mesataren raportet e seksionit të artë...

Marrëdhëniet në shkallë të gjerë midis sendeve, mjedisit të objektit dhe një personi veprojnë si një mjet harmonizimi, sepse shkalla është një nga manifestimet e proporcionalitetit, duke vendosur dimensione relative midis një personi dhe një objekti - në arkitekturë, në dizajn, në artin e aplikuar, në veçanti, në grafikën e aplikuar, në artin e librave. Kështu, madhësitë dhe formatet e posterave dhe çdo objekti që shërben për qëllimet e komunikimit vizual - shenjat, shenjat rrugore, etj., Si dhe zgjidhja e tyre kompozicionale zgjidhen gjithmonë në varësi të qëllimit dhe kushteve të funksionimit, dhe për këtë arsye në marrëdhëniet përkatëse të shkallës. . E njëjta gjë vlen edhe për fushën e dizajnit të librave dhe të gjitha llojet e reklamave dhe paketimeve të printuara.

Simetria.

Në proporcion dhe proporcionalitet manifestohen marrëdhëniet sasiore ndërmjet pjesëve të së tërës dhe të tërës. Grekët ua shtuan edhe simetrinë, duke e konsideruar si një lloj proporcionaliteti – si rast të veçantë – identitet. Ajo, si proporcioni, konsiderohej një kusht i domosdoshëm për harmoninë dhe bukurinë.

Simetria bazohet në ngjashmëri. Do të thotë një marrëdhënie e tillë midis elementeve dhe figurave kur ato përsërisin dhe balancojnë njëra-tjetrën. Në matematikë, simetri nënkupton shtrirjen e pjesëve të një figure kur e lëvizni atë në lidhje me një bosht ose qendër simetrie.

Ka lloje të ndryshme të simetrisë. Lloji më i thjeshtë i simetrisë është pasqyra (boshtore), e cila ndodh kur një figurë rrotullohet rreth një boshti simetrie. Simetria që ndodh kur një figurë rrotullohet rreth qendrës së rrotullimit quhet qendrore. Topi ka shkallën më të lartë të simetrisë, pasi një numër i pafund boshtesh dhe planesh simetrie kryqëzohen në qendër të tij. Simetria absolute, e ngurtë është karakteristikë e natyrës së pajetë - kristaleve (minerale, flokeve të borës).

Natyra organike dhe organizmat e gjallë karakterizohen nga simetri jo e plotë (kuazi-simetri), (për shembull, në strukturën e një personi). Shkelja e simetrisë, asimetrisë (mungesa e simetrisë) përdoret në art si një mjet artistik. Një devijim i lehtë nga simetria e saktë, domethënë njëfarë asimetrie, duke prishur ekuilibrin, tërheq vëmendjen, fut një element lëvizjeje dhe krijon përshtypjen e një forme të gjallë. Llojet e ndryshme të simetrisë kanë efekte të ndryshme në sensin estetik:

simetri pasqyrë - ekuilibër, paqe;
Simetria spirale ngjall një ndjenjë lëvizjeje...

Khzmbidj i klasifikon të gjitha figurat e thjeshta gjeometrike si simetri statike (duke i ndarë të gjitha llojet e simetrisë në statike dhe dinamike), dhe përfshin një spirale si simetri dinamike. Simetria statike shpesh bazohet në një pesëkëndësh (prerja e një lule ose fruti) ose një katror (në minerale). Në art, simetria e rreptë matematikore përdoret rrallë.

Oriz. 20. Llojet e simetrisë: Pasqyrë, spirale, qendrore, prerëse.

Oriz. 21. "The Line of Grace and Beauty" nga Hogarth

Simetria lidhet me konceptin e mesit dhe të tërësisë. Në filozofinë dhe artin e lashtë grek, koncepti i "mesit, qendrës" shoqërohet me idenë e integritetit të qenies. E mesme - "shmangia e ekstremeve" (Aristoteli) - nënkupton parimin e ekuilibrit. Kudo greku pa diçka të tërë dhe kjo do të thotë se ai para së gjithash fiksoi qendrën e objektit të vëzhguar ose të huaj... Pa konceptin e "mesit" mësimi i lashtë rreth përmasave, masës, simetrisë ose harmonisë është i paimagjinueshëm.

Harmonia

Harmonia është një koncept dialektik. Sipas mitologjisë së lashtë greke, Harmonia është e bija e perëndisë së luftës Ares dhe perëndeshës së dashurisë dhe bukurisë Afërdita, domethënë, parimet e kundërta, ndërluftuese janë shkrirë në të. Prandaj, koncepti i harmonisë përfshin kontrastin si kusht të domosdoshëm. Kontrasti promovon diversitetin dhe diversitetin, pa të cilin harmonia është e paimagjinueshme.

"Harmonia është uniteti i shumë njerëzve dhe pajtimi i atyre që nuk pajtohen"(Philolaus). Të lashtët e dinin këtë. Artisti i shekullit të 18-të Hogarth zbuloi se thelbi i harmonisë ishte në unitet dhe diversitet. Ai adhuronte vijën e valëzuar, të cilën ai e konsideronte " linjë e bukurisë dhe hirit", sepse është mishërimi konkret i unitetit dhe diversitetit. Pa diversitet, bukuria është e pamundur. Monotonia është e lodhshme. Në ndryshimin e të kundërtës, manifestohet një model dialektik - mohimi i mohimit. Në imazhet e dukshme të artit, është e shprehur përmes ritmit dhe kontrastit Kuptimi i harmonisë është frenimi i kaosit.

Por ajo e bën këtë përmes luftës së parimeve të kundërta. Duke bashkuar parimet e kundërta, harmonia i balancon ato, fut masën dhe marrëveshjen, i vë në rregull dhe e merr bukurinë si shpërblim.

Simetria, përmasat, ritmi, kontrasti, integriteti - ato që formojnë harmoninë janë objektivisht të lidhura me natyrën, me lëvizjen dhe zhvillimin e materies. Idetë tona estetike janë të lidhura ngushtë me këto koncepte. Megjithatë, ekzistenca shoqërore e njeriut në periudha të ndryshme i shikonte kategoritë e harmonisë nga këndvështrime të ndryshme, dhe kjo përcaktoi rolin e tyre në jetën shoqërore dhe në art. Ideja e bukurisë u zhvillua dhe ndryshoi. Harmonia filloi të shikohej jo si një parim sasior, por si një parim cilësor, duke bashkuar parimet fizike dhe shpirtërore.

Nëse grekët e lashtë e konsideronin të bukur vetëm bukurinë e urdhëruar dhe e shihnin të shëmtuar çdo shkelje të simetrisë dhe përmasave, atëherë në epokat pasuese manifestimet e bukurisë filluan të gjenden në shkelje të rendit, në disonancë, në disharmoninë e dukshme, sepse ato janë karakteristikë e jetës. dhe, për rrjedhojë, janë pjesë e një sistemi tjetër harmonik, në të cilin ata gjejnë logjikë dhe kuptim. "E bukura është jeta," shkroi Chernyshevsky. Dhe ajo nuk qëndron ende. Shfaqja e harmonisë në natyrë dhe jetë është më e gjerë se çdo kanun, çdo sistem harmonik mund të mbulojë. Dhe njerëzimi nuk do të ndalet kurrë së kërkuari për marrëdhënie të reja harmonike, kombinime dhe kërkim për manifestime të modeleve të tjera hermonike. Megjithatë, kjo nuk do të thotë se harmonia klasike ka humbur kuptimin e saj. Ajo që tashmë është zbuluar, ato modele të gjetura, justifikimi i tyre matematikor, mbeten trashëgimia e përjetshme e njerëzimit, nga e cila do të nxjerrin të gjithë brezat pasardhës.

shkoni në pjesën tjetër - ""

Nëse shikoni përreth me kujdes, roli i matematikës në jetën e njeriut bëhet i dukshëm. Kompjuterët, telefonat modernë dhe pajisjet e tjera na shoqërojnë çdo ditë dhe krijimi i tyre është i pamundur pa përdorimin e ligjeve dhe llogaritjeve të shkencës së madhe. Megjithatë, roli i matematikës në shoqëri nuk është i kufizuar në aplikime të tilla. Përndryshe, për shembull, shumë artistë mund të thonë me ndërgjegje të pastër se koha e kushtuar zgjidhjes së problemeve dhe vërtetimit të teoremave në shkollë ishte e humbur. Megjithatë, ky nuk është rasti. Le të përpiqemi të kuptojmë pse është e nevojshme matematika.

Baza

Së pari, ia vlen të kuptojmë se çfarë është në të vërtetë matematika. Përkthyer nga greqishtja e lashtë, vetë emri i saj do të thotë "shkencë", "studim". Matematika bazohet në veprimet e numërimit, matjes dhe përshkrimit të formave të objekteve. mbi të cilat bazohen njohuritë për strukturën, rendin dhe marrëdhëniet. Ato janë thelbi i shkencës. Vetitë e objekteve reale idealizohen në të dhe shkruhen në një gjuhë zyrtare. Kështu shndërrohen në objekte matematikore. Disa veti të idealizuara bëhen aksioma (pohime që nuk kërkojnë prova). Nga këto veçori të tjera të vërteta rrjedhin më pas. Kështu formohet një objekt real ekzistues.

Dy seksione

Matematika mund të ndahet në dy pjesë plotësuese. Shkenca teorike merret me analiza të thella të strukturave brenda-matematikore. Shkenca e aplikuar ofron modelet e saj për disiplina të tjera. Fizika, kimia dhe astronomia, sistemet inxhinierike, parashikimi dhe logjika përdorin vazhdimisht aparatin matematikor. Me ndihmën e tij bëhen zbulime, zbulohen modele dhe parashikohen ngjarje. Në këtë kuptim, rëndësia e matematikës në jetën e njeriut nuk mund të mbivlerësohet.

Baza e veprimtarisë profesionale

Pa njohuri për ligjet themelore matematikore dhe aftësinë për t'i përdorur ato, në botën moderne bëhet shumë e vështirë të mësosh pothuajse çdo profesion. Jo vetëm financierët dhe kontabilistët merren me numrat dhe operacionet me ta. Pa një njohuri të tillë, një astronom nuk do të jetë në gjendje të përcaktojë distancën nga ylli dhe kohën më të mirë për ta vëzhguar atë, dhe një biolog molekular nuk do të jetë në gjendje të kuptojë se si të merret me mutacionin e gjeneve. Një inxhinier nuk do të projektojë një sistem alarmi ose video survejimi, dhe një programues nuk do të gjejë një qasje ndaj sistemit operativ. Shumë nga këto dhe profesione të tjera thjesht nuk ekzistojnë pa matematikë.

shkencat humane

Megjithatë, roli i matematikës në jetën e një personi, për shembull, që i është përkushtuar pikturës ose letërsisë, nuk është aq i dukshëm. E megjithatë, gjurmët e mbretëreshës së shkencave janë të pranishme edhe në shkencat humane.

Duket se poezia është romancë dhe frymëzim i pastër, nuk ka vend për analiza dhe llogaritje. Megjithatë, mjafton të kujtohen përmasat poetike të amfibrakëve) dhe arrihet të kuptohet se edhe matematika ka pasur gisht në këtë. Ritmi, verbal ose muzikor, gjithashtu përshkruhet dhe llogaritet duke përdorur njohuritë e kësaj shkence.

Për një shkrimtar ose psikolog, koncepte të tilla si besueshmëria e informacionit, një incident i izoluar, përgjithësimi, e kështu me radhë janë shpesh të rëndësishme. Të gjitha ato janë ose drejtpërdrejt matematikore, ose janë ndërtuar mbi bazën e ligjeve të zhvilluara nga mbretëresha e shkencave dhe ekzistojnë falë saj dhe sipas rregullave të saj.

Psikologjia lindi në kryqëzimin e shkencave humane dhe natyrore. Të gjitha drejtimet e tij, edhe ato që punojnë ekskluzivisht me imazhe, mbështeten në vëzhgimin, analizën e të dhënave, përgjithësimin dhe verifikimin e tyre. Këtu përdoren metoda modelimi, parashikimi dhe statistikore.

Nga shkolla

Matematika është e pranishme në jetën tonë jo vetëm në procesin e zotërimit të një profesioni dhe zbatimin e njohurive të marra. Në një mënyrë apo tjetër, ne përdorim mbretëreshën e shkencave pothuajse në çdo moment të kohës. Kjo është arsyeja pse matematika fillon të mësohet mjaft herët. Duke zgjidhur probleme të thjeshta dhe komplekse, fëmija nuk mëson vetëm të mbledhë, të zbresë dhe të shumëzojë. Ai ngadalë, nga bazat, e kupton strukturën e botës moderne. Dhe ne nuk po flasim për përparimin teknik ose aftësinë për të kontrolluar ndryshimin në një dyqan. Matematika formon veçori të caktuara të të menduarit dhe ndikon në qëndrimin tonë ndaj botës.

Më e thjeshta, më e vështira, më e rëndësishmja

Ndoshta të gjithë do të kujtojnë të paktën një mbrëmje ndërsa bënin detyrat e shtëpisë, kur donin të ulërinin dëshpërimisht: "Nuk e kuptoj për çfarë është matematika!", hidhni mënjanë problemet e urryera komplekse dhe të lodhshme dhe vraponi në oborr me miqtë. Në shkollë dhe madje edhe më vonë, në kolegj, garancitë e prindërve dhe mësuesve se "do t'ju vijë në punë më vonë" duken si marrëzi të bezdisshme. Megjithatë, rezulton se ata kanë të drejtë.

Është matematika, dhe më pas fizika, ajo që të mëson të gjesh marrëdhëniet shkak-pasojë, krijon zakonin e kërkimit të famëkeqit "nga ku rriten këmbët". Vëmendje, përqendrim, vullnet - ata gjithashtu stërviten në procesin e zgjidhjes së atyre problemeve shumë të urryera. Nëse shkojmë më tej, aftësia për të nxjerrë pasoja nga faktet, për të parashikuar ngjarje të ardhshme dhe gjithashtu për të bërë të njëjtën gjë përcaktohet gjatë studimit të teorive matematikore. Modelimi, abstraksioni, deduksioni dhe induksioni janë të gjitha shkenca dhe në të njëjtën kohë mënyra të punës së trurit me informacionin.

Dhe përsëri psikologji

Shpesh është matematika ajo që i jep një fëmije zbulimin se të rriturit nuk janë të gjithëfuqishëm dhe nuk dinë gjithçka. Kjo ndodh kur mami ose babi, kur u kërkohet të ndihmojnë në zgjidhjen e një problemi, thjesht ngrenë supet dhe deklarojnë paaftësinë e tyre për ta bërë atë. Dhe fëmija detyrohet të kërkojë vetë përgjigjen, të bëjë gabime dhe të shikojë përsëri. Ndodh gjithashtu që prindërit thjesht refuzojnë të ndihmojnë. “Duhet ta bësh vetë”, thonë ata. Dhe ata e bëjnë atë siç duhet. Pas shumë orësh përpjekjesh, fëmija do të marrë jo vetëm detyrat e shtëpisë së përfunduar, por aftësinë për të gjetur në mënyrë të pavarur zgjidhje, për të zbuluar dhe korrigjuar gabimet. Dhe ky qëndron edhe roli i matematikës në jetën e njeriut.

Sigurisht, pavarësia, aftësia për të marrë vendime, për të qenë përgjegjës për to dhe mungesa e frikës nga gabimet zhvillohen jo vetëm në mësimet e algjebrës dhe gjeometrisë. Por këto disiplina luajnë një rol të rëndësishëm në proces. Matematika nxit cilësi të tilla si vendosmëria dhe aktiviteti. Vërtetë, shumë varet nga mësuesi. Paraqitja e gabuar e materialit, ashpërsia e tepërt dhe presioni, përkundrazi, mund të ngjall frikë nga vështirësitë dhe gabimet (së pari në klasë dhe më pas në jetë), hezitimin për të shprehur mendimin e dikujt dhe pasivitetin.

Matematika në jetën e përditshme

Pas mbarimit të universitetit apo kolegjit, të rriturit nuk reshtin së zgjidhuri problemet matematikore çdo ditë. Si të kapni trenin? A mund të gatuajë një kilogram mish darkë për dhjetë të ftuar? Sa kalori ka në pjatë? Sa do të zgjasë një llambë? Këto dhe shumë pyetje të tjera lidhen drejtpërdrejt me Mbretëreshën e Shkencave dhe nuk mund të zgjidhen pa të. Rezulton se matematika është pothuajse vazhdimisht e pranishme në mënyrë të padukshme në jetën tonë. Dhe më shpesh ne as nuk e vërejmë atë.

Matematika në jetën e shoqërisë dhe të individit prek një numër të madh fushash. Disa profesione janë të paimagjinueshme pa të, shumë u shfaqën vetëm falë zhvillimit të zonave të saj individuale. Progresi teknik modern është i lidhur ngushtë me ndërlikimin dhe zhvillimin e aparatit matematikor. Kompjuterët dhe telefonat, aeroplanët dhe anijet kozmike nuk do të shfaqeshin kurrë nëse njerëzit nuk do ta kishin njohur mbretëreshën e shkencave. Megjithatë, roli i matematikës në jetën e njeriut nuk përfundon me kaq. Shkenca e ndihmon një fëmijë të zotërojë botën, e mëson atë të ndërveprojë me të në mënyrë më efektive dhe të formësojë të menduarit e tij dhe tiparet e karakterit individual. Megjithatë, vetëm matematika nuk do të përballonte detyra të tilla. Siç u përmend më lart, prezantimi i materialit dhe tiparet e personalitetit të atij që e prezanton fëmijën me botën luan një rol të madh.

Dizajni efektiv modern i uebit nuk duhet të jetë vetëm një imazh i bukur dhe i ndezur. Duhet të jetë e thjeshtë dhe intuitive. Me çfarë mjetesh mund të arrihet kjo? Si ta bëni vizitorin të ndjejë një ndjenjë harmonie dhe rehatie? Dhe këtu matematika do të na vijë në ndihmë. Tani për tani, le të shohim se si funksionojnë disa rregulla themelore të matematikës në web design. Ne do ta shikojmë këtë duke përdorur shembullin e rregullit të raportit të artë, numrat e Fibonaçit, rregullin e pesë elementeve, luhatjet e valëve sinus dhe rregullin e të tretave.

Matematika është e mrekullueshme. Për një person larg numrave dhe ekuacioneve, kjo mund të tingëllojë absurde. Megjithatë, shumë nga gjërat më të bukura në natyrë, dhe vetë Universi, bazohen në përmasa të rrepta matematikore. Edhe Aristoteli, një nga filozofët më autoritativë të antikitetit, tha: "Matematika zbulon rendin, simetrinë dhe sigurinë, dhe këto janë llojet më të rëndësishme të bukurisë".

Për shekuj me radhë, matematika është përdorur si në art ashtu edhe në arkitekturë. Por matematika përdoret rrallë në hartimin e faqeve të internetit. Ndoshta sepse ekziston një besim i përbashkët se matematika dhe kreativiteti janë gjëra të papajtueshme. Edhe pse ky mendim mund të përgënjeshtrohet, matematika është e mirë mjet kur krijoni faqe interneti. Sidoqoftë, në këtë çështje nuk duhet të mbështeteni vetëm në matematikë. Këtu nevojitet diçka tjetër.

1. Raport i artë ose drejtkëndësh i artë
Raporti i artë (proporcioni i artë, ndarja në raport ekstrem dhe mesatar) është ndarja e një vlere të vazhdueshme në dy pjesë në një raport të tillë në të cilin pjesa më e vogël është e lidhur me atë më të madhen ashtu siç është ajo më e madhe me të gjithë vlerën. Raporti i pjesëve në këtë proporcion shprehet me një konstante matematikore irracionale të barabartë me afërsisht 1,618033987.

Në përgjithësi pranohet që objektet që përmbajnë "raportin e artë" perceptohen nga njerëzit si më harmonikët. Ja një fakt interesant nga Wikipedia. Dihet që Sergei Eisenstein ndërtoi artificialisht filmin "Battleship Potemkin" sipas rregullave të raportit të artë. Ai e theu shiritin në pesë pjesë.

Në tre të parat, veprimi zhvillohet në një anije. Në dy të fundit - në Odessa, ku po shpaloset kryengritja. Ky kalim në qytet ndodh pikërisht në pikën e raportit të artë. Dhe secila pjesë ka thyerjen e saj, e cila ndodh sipas ligjit të raportit të artë.

Tani le të kalojmë te Drejtkëndëshi i Artë. Gjithçka është e thjeshtë këtu. Për një drejtkëndësh të tillë, gjatësitë e anëve ngjitur janë të ndërlidhura sipas rregullit të seksionit të artë, d.m.th. 1:1.618.

Për të ndërtuar një drejtkëndësh të artë, fillimisht vizatoni një katror (në figurë me ngjyrë të kuqe), më pas vizatoni një vijë nga mesi i njërës prej anëve të katrorit në këndin e kundërt (vijë me një shigjetë në figurë). Ne e përdorim këtë vijë si rreze e harkut, e cila do të përcaktojë lartësinë e drejtkëndëshit. Tani përfundojmë vizatimin e drejtkëndëshit (ngjyra blu në foto).

Konsideroni këtë dizajn minimalist më poshtë si një shembull vizual. Ai përbëhet nga 6 drejtkëndësha të artë, me përmasa 299x185 piksele, 3 drejtkëndësha me radhë. Brinjët e këtyre drejtkëndëshave lidhen sipas rregullit të raportit të artë 299/185 = 1.616.

Vini re hapësirën e madhe rreth drejtkëndëshit të artë. Krijon një atmosferë të qetë dhe të këndshme në të cilën elementët e navigimit mund të marrin frymë lehtë. Pavarësisht përdorimit të vetëm disa ngjyrave dhe të njëjtit lloj blloqesh, të gjithë elementët e navigimit janë intuitiv dhe i shërbejnë qëllimit të tyre.

Për të shtuar një bllok të ri pa shkelur logjikën e dizajnit, është më e këshillueshme të shtoni blloqe në rreshtin e tretë dhe të lëvizni poshtë në një mënyrë të ngjashme.

Zonat e përdorimit. Përdorimi i Drejtkëndëshave të Artë në dizajn është i përshtatshëm për galeri të ndryshme fotografish, faqe portofoli dhe faqe të fokusuara në prezantimin e produktit.

2. Numrat e Fibonaçit në dizajn
Numrat Fibonacci janë një sekuencë matematikore numrash. Sipas përkufizimit, dy numrat e parë të Fibonaçit janë 0 dhe 1. Çdo numër i mëpasshëm është i barabartë me shumën e dy të mëparshmeve. Seria e numrave duket kështu: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Numrat Fibonacci përdoren në muzikë për të akorduar instrumentet, në arkitekturë për të llogaritur përmasa harmonike, për shembull, raporti i lartësisë së një dhome me lartësinë e dekorimit të murit me materiale të ndryshme. Distancat midis gjetheve (ose degëve) në trungun e një bime lidhen afërsisht me numrat e Fibonaçit.

Fusha kryesore e aplikimit të numrave Fibonacci në dizajn është përcaktimi i madhësisë së blloqeve me përmbajtjen kryesore (kontejnerët) dhe shiritat anësor. Thelbi i metodës është si më poshtë. Gjerësia e bazës së kontejnerit merret, për shembull, 90 piksel, dhe shumëzohet në mënyrë sekuenciale me numrat nga seria Fibonacci. Bazuar në këto llogaritje, ndërtohet një rrjet lokacioni. Le të shohim një shembull.

Faqja është e ndarë në tre kolona. Gjerësia e bazës së kontejnerit është 90 piksele. Pastaj kolona e parë është 180 piksel e gjerë (90 x 2), kolona e dytë është 270 piksele e gjerë (90 x 3) dhe kolona e tretë është 720 piksel e gjerë (90 x 8). Madhësia e shkronjave korrespondon gjithashtu me serinë Fibonacci. Madhësia e shkronjave të kokës është 55 px, fonti i seksionit është 34 px dhe fonti i tekstit është 21 px.

Nëse faqja ka një gjerësi fikse, për shembull 1000 piksele, atëherë numrat Fibonacci nuk janë shumë të përshtatshëm për t'u përdorur. Meqenëse numri më i afërt me 1000 nga seria Fibonacci është 987 (..., 610, 987, 1597...), atëherë është nga ky numër që do t'ju duhet të bëni llogaritjet për gjerësinë e blloqeve të faqes. Në situata të tilla, është më mirë të përdorni rregullin e raportit të artë (1000 x 0.618 = 618 px) dhe ta përdorni atë për të përcaktuar gjerësinë e blloqeve.

Zonat e përdorimit. Numrat Fibonacci janë më të përshtatshmet për hartimin e blogut dhe paraqitjet e revistave.

3. Pesë elementë ose dizajn Kundli
Një shembull tjetër interesant i matematikës në dizajn është një teknikë e bazuar në rregullat për përpilimin e horoskopit Indian Kundli. Baza këtu është figura e mëposhtme. Vizatohet një katror, brenda tij vizatohen dy diagonale, duke lidhur qoshet e kundërta, pastaj vijat lidhin qendrat e anëve ngjitur të sheshit.

Brenda sheshit shohim katër diamante. Kjo është baza për vendosjen e pesë elementeve të dizajnit në faqe.

Shembulli i dizajnit të faqes në internet më poshtë bazohet në gjeometrinë e Kundli. Ky plan urbanistik mund të jetë i përshtatshëm për një faqe interneti me një kartëvizitë me elemente ndërvepruese të dizajnit të bazuara në teknologjinë jQuery.

Gjithashtu, kjo paraqitje mund të shndërrohet lehtësisht në një faqe interneti me një plan urbanistik me tre kolona me një kokë dhe fund.

Zonat e përdorimit. Ky dizajn është më i përshtatshëm për faqet e portofolit dhe faqet e fokusuara në shfaqjen e produkteve.

4. Lëkundjet sinusoidale
Nëse dëshironi shumëllojshmëri, atëherë nuk është aspak e nevojshme t'i përmbaheni rregullave themelore të raportit të artë dhe numrave Fibonacci. Ju mund të eksperimentoni me formula të tjera të njohura.

Le të shohim se si do të dalë faqosja e faqes së internetit, bazuar në lëkundjet e një sinusoidi, një funksion matematikor që përshkruan luhatjet e përsëritura. Figura më poshtë tregon një shembull të një faqe interneti të thjeshtë dhe origjinale me një faqe.

Ose një opsion tjetër. Një plan urbanistik i përbërë nga një kokë, pesë kolona dhe një fund. Një sajt i tillë mund të përmirësohet edhe me këshilla veglash JQuery për ta bërë atë më interaktiv.

Zonat e përdorimit. Ky dizajn është optimal për faqet ku është e nevojshme të pasqyrohet kronologjia e ngjarjeve. Më e përshtatshme për lundrim horizontal.

5. Rregulli i të tretave
Ky rregull thotë se imazhi duhet të ndahet në nëntë pjesë të barabarta nga dy vija horizontale dhe dy vertikale. Dhe të gjithë elementët e rëndësishëm të përbërjes duhet të vendosen përgjatë këtyre linjave ose në kryqëzimet e tyre.

Në këtë shembull, dy nga katër kryqëzimet përmbajnë informacionin më të rëndësishëm. E shënuar me katrorë rozë. Dhe blloku i lundrimit ndodhet pikërisht përgjatë vijës së dytë horizontale.

Ndonjëherë duket se bota jonë është e thjeshtë dhe e kuptueshme. Në fakt, ky është misteri i madh i Universit, i cili krijoi një planet kaq të përsosur. Apo ndoshta është krijuar nga dikush që ndoshta e di se çfarë po bën? Mendjet më të mëdha të kohës sonë po punojnë për këtë çështje.

Çdo herë ata arrijnë në përfundimin se është e pamundur të krijojmë gjithçka që kemi pa Mendjen e Lartë. Sa i jashtëzakonshëm, kompleks dhe në të njëjtën kohë i thjeshtë dhe spontan është planeti ynë Tokë! Bota rreth nesh është e mahnitshme me rregullat, format dhe ngjyrat e saj.

Ligjet e natyrës

Gjëja e parë që mund t'i kushtoni vëmendje në planetin tonë të madh dhe të mahnitshëm është se ai gjendet në të gjitha format e botës përreth, dhe është gjithashtu parimi bazë i bukurisë, idealitetit dhe proporcionalitetit. Kjo nuk është gjë tjetër veçse matematikë në natyrë.

Koncepti i "simetrisë" do të thotë harmoni, korrektësi. Kjo është një veti e realitetit përreth që sistemon fragmente dhe i kthen ato në një tërësi të vetme. Në Greqinë e lashtë, shenjat e këtij ligji filluan të viheshin re për herë të parë. Për shembull, Platoni besonte se bukuria shfaqet vetëm si rezultat i simetrisë dhe proporcionalitetit. Në fakt, nëse shikojmë objekte që janë proporcionale, korrekte dhe të plota, atëherë gjendja jonë e brendshme do të jetë e bukur.

Ligjet e matematikës në natyrën e gjallë dhe të pajetë

Le të shohim çdo krijesë, për shembull më të përsosurin - njeriun. Do të shohim një strukturë trupore që duket e njëjtë në të dyja anët. Ju gjithashtu mund të listoni shumë shembuj, si insektet, kafshët, jetën detare, zogjtë. Çdo specie ka ngjyrën e vet.

Nëse ka ndonjë model ose dizajn, dihet se ai pasqyrohet rreth vijës qendrore. Të gjithë organizmat krijohen falë rregullave të universit. Modele të tilla matematikore mund të gjurmohen edhe në natyrën e pajetë.

Nëse i kushtoni vëmendje të gjitha fenomeneve, si tornado, ylber, bimë, fjolla dëbore, mund të gjeni shumë gjëra të përbashkëta në to. Një gjethe relativisht e një peme është e ndarë në gjysmë dhe secila pjesë do të jetë një reflektim i asaj të mëparshme.

Nëse marrim si shembull një tornado, i cili ngrihet vertikalisht dhe duket si një hinkë, atëherë mund të ndahet edhe në dy gjysma absolutisht identike. Dukurinë e simetrisë mund ta gjeni në ndryshimin e ditës dhe natës, stinëve. Ligjet e botës përreth janë matematikë në natyrë, e cila ka sistemin e vet të përsosur. I gjithë koncepti i krijimit të Universit mbështetet mbi të.

Ylber

Ne nuk mendojmë shpesh për fenomenet natyrore. Binte borë ose shi, doli dielli ose goditi bubullima - gjendja e zakonshme e ndryshimit të motit. Merrni parasysh harkun shumëngjyrësh që zakonisht mund të gjendet pas reshjeve. Një ylber në qiell është një fenomen natyror i mahnitshëm, i shoqëruar nga një spektër i të gjitha ngjyrave të dukshme vetëm për syrin e njeriut. Kjo ndodh për shkak të kalimit të rrezeve të diellit nëpër renë që largohet. Çdo pikë shiu shërben si një prizëm që ka veti optike. Mund të themi se çdo pikë është një ylber i vogël.

Duke kaluar nëpër një pengesë uji, rrezet ndryshojnë ngjyrën e tyre origjinale. Çdo rrymë drite ka një gjatësi dhe hije të caktuar. Kjo është arsyeja pse sytë tanë e perceptojnë një ylber si kaq shumëngjyrësh. Le të vërejmë një fakt interesant se ky fenomen mund të shihet vetëm nga njerëzit. Sepse është thjesht një iluzion.

Llojet e ylberit

Ylberët e formuar nga dielli janë më të zakonshmet. Është më e ndritura nga të gjitha varietetet. Përbëhet nga shtatë ngjyra kryesore: e kuqe portokalli, e verdhë, jeshile, blu, vjollcë, vjollcë. Por nëse shikojmë detajet, ka shumë më tepër nuanca sesa mund të shohin sytë tanë.
Një ylber i krijuar nga hëna ndodh natën. Besohet se mund të shihet gjithmonë. Por, siç tregon praktika, ky fenomen vërehet kryesisht vetëm në zonat me shi ose pranë ujëvarave të mëdha. Ngjyrat e ylberit hënor janë shumë të zbehta. Ata janë të destinuar të ekzaminohen vetëm me ndihmën e pajisjeve speciale. Por edhe me të, syri ynë mund të dallojë vetëm një rrip të bardhë.
Ylberi që shfaqet si pasojë e mjegullës është si një hark i gjerë ndriçues drite. Ndonjëherë ky lloj ngatërrohet me atë të mëparshëm. Ngjyra mund të jetë portokalli sipër dhe një nuancë vjollce poshtë. Rrezet e diellit që kalojnë nëpër mjegull formojnë një fenomen të bukur natyror.
shfaqet jashtëzakonisht rrallë në qiell. Nuk është i ngjashëm me llojet e mëparshme në formën e tij horizontale. Fenomeni është i mundur vetëm mbi retë cirruse. Zakonisht shtrihen në një lartësi prej 8-10 kilometrash. Këndi në të cilin ylberi do të shfaqet në të gjithë lavdinë e tij duhet të jetë më shumë se 58 gradë. Ngjyrat zakonisht mbeten të njëjta si në një ylber diellor.

Raporti i artë (1.618)

Proporcionaliteti ideal më së shpeshti mund të gjendet në botën e kafshëve. Atyre u jepet një proporcion që është i barabartë me rrënjën e numrit PHI që korrespondon me një. Ky raport është fakti lidhës i të gjitha kafshëve në planet. Mendjet e mëdha të antikitetit e quajtën këtë numër proporcioni hyjnor. Mund të quhet edhe raporti i artë.

Ky rregull është plotësisht në përputhje me harmoninë e strukturës njerëzore. Për shembull, nëse përcaktoni distancën midis syve dhe vetullave, ajo do të jetë e barabartë me konstanten hyjnore.

Raporti i artë është një shembull se sa e rëndësishme është matematika në natyrë, ligji i së cilës filloi të ndiqet nga stilistë, artistë, arkitektë dhe krijues të gjërave të bukura dhe të përsosura. Ata krijojnë me ndihmën e konstantës hyjnore krijimet e tyre, të cilat kanë ekuilibër, harmoni dhe janë të këndshme për t'u parë. Mendja jonë është në gjendje të konsiderojë të bukura ato gjëra, objekte, dukuri ku ka një raport të pabarabartë pjesësh. Truri ynë e quan raportin e artë proporcionalitet.

Spirale e ADN-së

Siç vuri në dukje me të drejtë shkencëtari gjerman Hugo Weyl, rrënjët e simetrisë erdhën përmes matematikës. Shumë vunë re përsosmërinë e formave gjeometrike dhe u kushtuan vëmendje atyre. Për shembull, një huall mjalti nuk është gjë tjetër veçse një gjashtëkëndësh i krijuar nga vetë natyra. Ju gjithashtu mund t'i kushtoni vëmendje koneve të bredhit, të cilat kanë një formë cilindrike. Spiralat gjithashtu gjenden shpesh në botën përreth: brirët e bagëtive të mëdha dhe të vogla, predha molusqesh, molekula të ADN-së.

Krijuar sipas parimit të raportit të artë. Është lidhja lidhëse midis diagramit të trupit material dhe imazhit të tij real. Dhe nëse marrim parasysh trurin, ai nuk është gjë tjetër veçse një përcjellës midis trupit dhe mendjes. Inteligjenca lidh jetën dhe formën e shfaqjes së saj dhe lejon që jeta e përfshirë në formë të njohë vetveten. Me ndihmën e kësaj, është e mundur që njerëzimi të kuptojë planetin përreth, të kërkojë modele në të, të cilat më pas zbatohen për studimin e botës së brendshme.

Ndarja në natyrë

Mitoza e qelizave përbëhet nga katër faza:

Profaza. Thelbi në të rritet. Shfaqen kromozome, të cilat fillojnë të përdredhohen në një spirale dhe kthehen në formën e tyre të zakonshme. Formohet një vend për ndarjen e qelizave. Në fund të fazës, bërthama dhe guaska e saj shpërndahen dhe kromozomet derdhen në citoplazmë. Kjo është faza më e gjatë e ndarjes.
Metafaza. Këtu përfundon spiralja e kromozomeve dhe ato formojnë pllakën metafazë. Kromatidet pozicionohen përballë njëra-tjetrës në përgatitje për ndarje. Midis tyre shfaqet një vend për shkëputje - një gisht. Kjo përfundon fazën e dytë.

Anafaza. Kromatidet ndryshojnë në drejtime të kundërta. Tani qeliza ka dy grupe kromozomesh për shkak të ndarjes së tyre. Kjo fazë është shumë e shkurtër.
Telofaza. Në secilën gjysmë të qelizës, formohet një bërthamë, brenda së cilës formohet një bërthamë. Citoplazma është e disociuar në mënyrë aktive. Gishti gradualisht zhduket.

Kuptimi i mitozës

Për shkak të metodës unike të ndarjes, çdo qelizë pasuese pas riprodhimit ka të njëjtën përbërje gjenesh si nëna e saj. Të dyja qelizat marrin të njëjtën përbërje kromozomesh. Kjo nuk mund të bëhej pa një shkencë të tillë si gjeometria. Progresi në mitozë është i rëndësishëm sepse ky është parimi me të cilin riprodhohen të gjitha qelizat.

Nga vijnë mutacionet?

Ky proces siguron një furnizim të vazhdueshëm të kromozomeve dhe materialeve gjenetike në çdo qelizë. Për shkak të mitozës, trupi zhvillohet, riprodhohet dhe rigjenerohet. Në rast të një shqetësimi për shkak të veprimit të disa helmeve, kromozomet mund të mos ndahen në gjysmat e tyre ose mund të shfaqin shqetësime strukturore. Ky do të jetë një tregues i qartë i mutacioneve fillestare.

Duke përmbledhur

Çfarë kanë të përbashkët matematika dhe natyra? Përgjigjen për këtë pyetje do ta gjeni në artikullin tonë. Dhe nëse gërmoni më thellë, duhet të thoni se duke studiuar botën përreth nesh, njeriu njeh veten. Pa Atë që lindi të gjitha gjallesat, asgjë nuk mund të kishte ndodhur. Natyra është ekskluzivisht në harmoni, në sekuencën strikte të ligjeve të saj. A është e mundur e gjithë kjo pa arsye?

Le të citojmë deklaratën e shkencëtarit, filozofit, matematikanit dhe fizikanit Henri Poincaré, i cili, si askush tjetër, mund t'i përgjigjet pyetjes nëse matematika në natyrë është me të vërtetë themelore. Disa materialistë mund të mos e pëlqejnë një arsyetim të tillë, por nuk ka gjasa që ata të jenë në gjendje ta hedhin poshtë atë. Poincaré thotë se harmonia që mendja njerëzore dëshiron të zbulojë në natyrë nuk mund të ekzistojë jashtë saj. e cila është e pranishme në mendjet e të paktën disa individëve mund të jetë e aksesueshme për të gjithë njerëzimin. Lidhja që bashkon aktivitetin mendor quhet harmonia e botës. Kohët e fundit ka pasur përparime kolosale drejt një procesi të tillë, por ato janë shumë të vogla. Këto lidhje që lidhin Universin dhe individin duhet të jenë të vlefshme për çdo mendje njerëzore që është e ndjeshme ndaj këtyre proceseve.

Si përfundim, do të përpiqemi të karakterizojmë shkurtimisht modelet e përgjithshme të zhvillimit të matematikës.

1. Matematika nuk është krijimi i asnjë epoke historike, asnjë populli; është produkt i një sërë epokash, produkt i punës së shumë brezave. U ngritën konceptet dhe dispozitat e para

siç e kemi parë, në kohët e lashta dhe tashmë më shumë se dy mijë vjet më parë ato u sollën në një sistem harmonik. Pavarësisht nga të gjitha transformimet e matematikës, konceptet dhe përfundimet e saj ruhen, duke kaluar nga një epokë në tjetrën, siç janë, për shembull, rregullat e aritmetikës ose teorema e Pitagorës.

Teoritë e reja përfshijnë arritjet e mëparshme, duke i qartësuar, plotësuar dhe përgjithësuar ato.

Në të njëjtën kohë, siç është e qartë nga përshkrimi i shkurtër i historisë së matematikës të dhënë më sipër, zhvillimi i saj jo vetëm që nuk mund të reduktohet në një grumbullim të thjeshtë të teoremave të reja, por përfshin ndryshime të rëndësishme dhe cilësore. Prandaj, zhvillimi i matematikës ndahet në një numër periudhash, kalimet midis të cilave tregohen saktësisht nga ndryshime të tilla themelore në vetë lëndën ose strukturën e kësaj shkence.

Matematika përfshin në sferën e saj të gjitha fushat e reja të marrëdhënieve sasiore të realitetit. Në të njëjtën kohë, lënda më e rëndësishme e matematikës ka qenë dhe mbetet format hapësinore dhe marrëdhëniet sasiore në kuptimin e thjeshtë, më të drejtpërdrejtë të këtyre fjalëve, dhe kuptimi matematik i lidhjeve dhe marrëdhënieve të reja ndodh në mënyrë të pashmangshme në bazë dhe në lidhje me sistemi tashmë i krijuar i koncepteve shkencore sasiore dhe hapësinore.

Së fundi, akumulimi i rezultateve brenda vetë matematikës kërkon domosdoshmërisht një ngjitje në nivele të reja abstraksioni, në koncepte të reja përgjithësuese dhe një thellim në analizën e themeleve dhe koncepteve fillestare.

Ashtu si një pemë lisi në rritjen e tij të fuqishme i trash degët e vjetra me shtresa të reja, nxjerr degë të reja, shtrihet lart dhe thellohet me rrënjët e saj poshtë, ashtu edhe matematika në zhvillimin e saj grumbullon materiale të reja në zonat e saj tashmë të krijuara, formon drejtime të reja, ngjitet në lartësi të reja të abstraksionit dhe shkon më thellë në bazat e tij.

2. Matematika ka si lëndë format reale dhe marrëdhëniet e realitetit, por, siç thoshte Engelsi, për t'i studiuar këto forma dhe marrëdhënie në formën e tyre të pastër, është e nevojshme t'i veçojmë plotësisht nga përmbajtja e tyre, duke lënë mënjanë këtë të fundit si. diçka indiferente. Megjithatë, format dhe marrëdhëniet nuk ekzistojnë jashtë përmbajtjes dhe marrëdhëniet matematikore nuk mund të jenë absolutisht indiferente ndaj përmbajtjes. Prandaj, matematika, e cila në thelb përpiqet të arrijë një ndarje të tillë, përpiqet të arrijë të pamundurën. Kjo është një kontradiktë themelore në thelbin e matematikës. Është një manifestim specifik i matematikës i kontradiktës së përgjithshme të njohjes. Reflektimi me mendim i çdo dukurie, çdo anë, çdo moment të realitetit e rëndon, e thjeshton atë, duke e rrëmbyer nga lidhja e përgjithshme e natyrës. Kur njerëzit, duke studiuar vetitë e hapësirës, konstatuan se ajo ka gjeometri Euklidiane, një gjë e jashtëzakonshme

një akt i rëndësishëm njohjeje, por përmbante edhe një iluzion: vetitë reale të hapësirës [të marra në një mënyrë të thjeshtuar, skematike, në abstragim nga materia. Por pa këtë, thjesht nuk do të kishte gjeometri, dhe pikërisht në bazë të këtij abstraksioni (si nga kërkimet e tij të brendshme ashtu edhe nga krahasimi i rezultateve matematikore me të dhënat e reja nga shkencat e tjera) lindën dhe u forcuan teoritë e reja gjeometrike.

Zgjidhja dhe rivendosja e vazhdueshme e kësaj kontradikte në fazat e njohjes që janë gjithnjë e më afër realitetit përbën thelbin e zhvillimit të njohjes. Në këtë rast, faktori përcaktues është sigurisht përmbajtja pozitive e dijes, elementi i së vërtetës absolute në të. Njohuria lëviz përgjatë një linje ngjitëse dhe nuk shënon kohën, thjesht e përzier me gabim. Lëvizja e dijes është një tejkalim i vazhdueshëm i pasaktësisë dhe kufizimeve të saj.

Kjo kontradiktë kryesore sjell të tjera. Këtë e pamë në shembullin e të kundërtave të diskrete dhe të vazhdueshme. (Në natyrë nuk ka asnjë hendek absolut midis tyre, dhe ndarja e tyre në matematikë në mënyrë të pashmangshme shkaktoi nevojën për të krijuar koncepte gjithnjë e më të reja që pasqyrojnë më thellë realitetin dhe në të njëjtën kohë kapërcejnë papërsosmëritë e brendshme të teorisë ekzistuese matematikore). Pikërisht në të njëjtën mënyrë, kontradiktat e së fundmit dhe së pafundmes, abstraktes dhe konkretes, formës dhe përmbajtjes, etj., shfaqen në matematikë si shfaqje të kontradiktës së saj themelore. Por manifestimi i saj vendimtar është se, duke abstraguar nga konkretja, duke u rrotulluar në rrethin e koncepteve të saj abstrakte, matematika ndahet në këtë mënyrë nga eksperimenti dhe praktika, dhe në të njëjtën kohë ajo është vetëm një shkencë (d.m.th. ka vlerë njohëse) për aq sa mbështetet. në praktikë, pasi rezulton të jetë jo e pastër, por matematikë e aplikuar. Për ta thënë disi në gjuhën hegeliane, matematika e pastër vazhdimisht e “mohon” veten si matematikë e pastër pa këtë ajo nuk mund të ketë domethënie shkencore, nuk mund të zhvillohet, nuk mund t'i kapërcejë vështirësitë që lindin në mënyrë të pashmangshme brenda saj.

Në formën e tyre formale, teoritë matematikore i kundërvihen përmbajtjes reale si disa skema për përfundime specifike. Në këtë rast, matematika vepron si një metodë për formulimin e ligjeve sasiore të shkencës natyrore, si një aparat për zhvillimin e teorive të saj, si një mjet për zgjidhjen e problemeve në shkencën dhe teknologjinë natyrore. Rëndësia e matematikës së pastër në fazën e tanishme qëndron kryesisht në metodën matematikore. Dhe ashtu si çdo metodë ekziston dhe zhvillohet jo më vete, por vetëm në bazë të aplikimeve të saj, në lidhje me përmbajtjen në të cilën zbatohet, ashtu edhe matematika nuk mund të ekzistojë dhe të zhvillohet pa aplikime. Këtu përsëri zbulohet uniteti i të kundërtave: metoda e përgjithshme i kundërvihet një problemi specifik si mjet për zgjidhjen e tij, por ajo vetë lind nga një përgjithësim i materialit specifik dhe ekziston.

zhvillohet dhe e gjen justifikimin e saj vetëm në zgjidhjen e problemeve specifike.

3. Praktika sociale luan një rol vendimtar në zhvillimin e matematikës në tre aspekte. Ai shtron probleme të reja për matematikën, stimulon zhvillimin e saj në një drejtim ose në një tjetër dhe ofron një kriter për vërtetësinë e përfundimeve të saj.

Kjo mund të shihet jashtëzakonisht qartë në shfaqjen e analizës. Së pari, ishte zhvillimi i mekanikës dhe teknologjisë që ngriti problemin e studimit të varësive të variablave në formën e tyre të përgjithshme. Arkimedi, pasi iu afrua llogaritjes diferenciale dhe integrale, mbeti megjithatë brenda kuadrit të problemeve statike, ndërsa në kohët moderne ishte studimi i lëvizjes ai që lindi konceptet e ndryshores dhe funksionit dhe detyroi formulimin e analizës. Njutoni nuk mund të zhvillonte mekanikën pa zhvilluar një metodë matematikore përkatëse.

Së dyti, ishin pikërisht nevojat e prodhimit shoqëror që nxitën formulimin dhe zgjidhjen e të gjitha këtyre problemeve. As në shoqërinë e lashtë dhe as në atë mesjetare nuk ekzistonin këto stimuj. Së fundi, është shumë karakteristike që analiza matematikore, në fillimet e saj, gjeti justifikim për përfundimet e saj pikërisht në aplikime. Kjo është e vetmja arsye pse ai mund të zhvillohet pa ato përkufizime strikte të koncepteve të tij bazë (ndryshore, funksion, kufi) që u dhanë më vonë. E vërteta e analizës u vërtetua nga aplikimet në mekanikë, fizikë dhe teknologji.

Sa më sipër vlen për të gjitha periudhat e zhvillimit të matematikës. Që nga shekulli i 17-të. Ndikimin më të drejtpërdrejtë në zhvillimin e tij e kanë, së bashku me mekanikën, fizika teorike dhe problemet e teknologjisë së re. Mekanika e vazhdimësisë, dhe më pas teoria e fushës (përçueshmëria termike, elektriciteti, magnetizmi, fusha gravitacionale) udhëheqin zhvillimin e teorisë së ekuacioneve diferenciale të pjesshme. Zhvillimi i teorisë molekulare dhe fizikës statistikore në përgjithësi, duke filluar nga fundi i shekullit të kaluar, shërbeu si një stimul i rëndësishëm për zhvillimin e teorisë së probabilitetit, veçanërisht teorisë së proceseve të rastësishme. Teoria e relativitetit luajti një rol vendimtar në zhvillimin e gjeometrisë Riemanniane me metodat dhe përgjithësimet e saj analitike.

Aktualisht, zhvillimi i teorive të reja matematikore, si analiza funksionale, etj., nxitet nga problemet e mekanikës kuantike dhe elektrodinamikës, problemet e teknologjisë kompjuterike, çështjet statistikore të fizikës dhe teknologjisë, etj., etj. Fizika dhe teknologjia nuk paraqesin vetëm sfidat e reja të problemeve të matematikës, e shtyjnë atë drejt lëndëve të reja kërkimore, por zgjojnë edhe zhvillimin e degëve të matematikës të nevojshme për to, të cilat fillimisht u zhvilluan kryesisht brenda vetes, siç ishte rasti me gjeometrinë Riemanniane. Shkurtimisht, për zhvillimin intensiv të shkencës është e nevojshme që jo vetëm t'i qaset zgjidhjes së problemeve të reja, por të imponohet nevoja për zgjidhjen e tyre.

nevojat e zhvillimit të shoqërisë. Në matematikë, kohët e fundit janë shfaqur shumë teori, por vetëm ato prej tyre janë zhvilluar dhe janë futur fort në shkencë që kanë gjetur aplikimet e tyre në shkencën dhe teknologjinë natyrore ose kanë luajtur rolin e përgjithësimeve të rëndësishme të atyre teorive që kanë aplikime të tilla. Në të njëjtën kohë, teoritë e tjera mbeten pa lëvizje, si p.sh., disa teori të rafinuara gjeometrike (gjeometritë jo-desargeziane, jo-arkimediane), të cilat nuk kanë gjetur zbatime të rëndësishme.

E vërteta e konkluzioneve matematikore e gjen bazën e saj përfundimtare jo në përkufizime dhe aksioma të përgjithshme, jo në ashpërsinë formale të provave, por në aplikime reale, pra në fund të fundit në praktikë.

Në përgjithësi, zhvillimi i matematikës duhet kuptuar kryesisht si rezultat i ndërveprimit të logjikës së lëndës së saj, i pasqyruar në logjikën e brendshme të vetë matematikës, ndikimin e prodhimit dhe lidhjet me shkencën natyrore. Ky ndryshim ndjek rrugë komplekse të luftës midis të kundërtave, duke përfshirë ndryshime të rëndësishme në përmbajtjen dhe format bazë të matematikës. Për nga përmbajtja, zhvillimi i matematikës përcaktohet nga lënda e saj, por stimulohet kryesisht dhe në fund të fundit nga nevojat e prodhimit. Ky është modeli bazë i zhvillimit të matematikës.

Natyrisht, nuk duhet të harrojmë se po flasim vetëm për modelin bazë dhe se lidhja midis matematikës dhe prodhimit, në përgjithësi, është komplekse. Nga sa u tha më sipër, është e qartë se do të ishte naive të përpiqeshim të justifikonim shfaqjen e secilës teori të caktuar matematikore me një "urdhër prodhimi" të drejtpërdrejtë. Për më tepër, matematika, si çdo shkencë, ka pavarësi relative, logjikën e saj të brendshme, duke reflektuar, siç e kemi theksuar, logjikën objektive, d.m.th., rregullsinë e lëndës së saj.

4. Matematika ka përjetuar gjithmonë ndikimin më domethënës jo vetëm të prodhimit shoqëror, por edhe të të gjitha kushteve shoqërore në përgjithësi. Përparimi i saj i shkëlqyer në epokën e ngritjes së Greqisë së lashtë, suksesi i algjebrës në Itali gjatë Rilindjes, zhvillimi i analizës në epokën që pasoi Revolucionin Anglez, suksesi i matematikës në Francë në periudhën ngjitur me Revolucionin Francez. - e gjithë kjo tregon bindshëm lidhjen e pazgjidhshme të përparimit të matematikës me përparimin e përgjithshëm teknik, kulturor, politik të shoqërisë.

Kjo shihet qartë edhe në zhvillimin e matematikës në Rusi. Formimi i një shkolle të pavarur matematikore ruse, që vjen nga Lobachevsky, Ostrogradsky dhe Chebyshev, nuk mund të ndahet nga përparimi i shoqërisë ruse në tërësi. Koha e Lobachevsky është koha e Pushkinit,

Glinka, koha e Decembristëve dhe lulëzimi i matematikës ishte një nga elementët e ngritjes së përgjithshme.

Aq më bindës është ndikimi i zhvillimit shoqëror në periudhën pas Revolucionit të Madh Socialist të Tetorit, kur studimet me rëndësi themelore u shfaqën njëri pas tjetrit me shpejtësi të mahnitshme në shumë drejtime: në teorinë e grupeve, topologjinë, teorinë e numrave, teorinë e probabilitetit, teorinë e ekuacionet diferenciale, analiza funksionale, algjebër, gjeometri.

Së fundi, matematika ka qenë gjithmonë dhe vazhdon të ndikohet ndjeshëm nga ideologjia. Si në çdo shkencë, përmbajtja objektive e matematikës perceptohet dhe interpretohet nga matematikanët dhe filozofët brenda kornizës së një ideologjie ose një tjetër.

Shkurt, përmbajtja objektive e shkencës përshtatet gjithmonë në një formë ideologjike ose në një tjetër; uniteti dhe lufta e këtyre të kundërtave dialektike - përmbajtjes objektive dhe formave ideologjike - në matematikë, si në çdo shkencë, luajnë një rol të rëndësishëm në zhvillimin e saj.

Lufta midis materializmit, i cili korrespondon me përmbajtjen objektive të shkencës, dhe idealizmit, i cili kundërshton këtë përmbajtje dhe shtrembëron kuptimin e tij, kalon në të gjithë historinë e matematikës. Kjo luftë u tregua qartë tashmë në Greqinë e lashtë, ku idealizmi i Pitagorës, Sokratit dhe Platonit kundërshtoi materializmin e Talesit, Demokritit dhe filozofëve të tjerë që krijuan matematikën greke. Me zhvillimin e sistemit të skllevërve, elita e shoqërisë u shkëput nga pjesëmarrja në prodhim, duke e konsideruar atë si fat të shtresës së ulët, dhe kjo shkaktoi një ndarje të shkencës "të pastër" nga praktika. Vetëm gjeometria thjesht teorike u njoh si e denjë për vëmendjen e një filozofi të vërtetë. Është karakteristikë që Platoni i konsideroi studimet e shfaqura të disa kthesave mekanike, madje edhe seksioneve konike, të mbesin jashtë kufijve të gjeometrisë, pasi ato "nuk na sjellin në komunikim me ide të përjetshme dhe jotrupore" dhe "kanë nevojë për përdorimin e veglave vulgare. zeje.”

Një shembull i mrekullueshëm i luftës së materializmit kundër idealizmit në matematikë është veprimtaria e Lobachevsky, i cili parashtroi dhe mbrojti kuptimin materialist të matematikës kundër pikëpamjeve idealiste të Kantianizmit.

Shkolla matematikore ruse në përgjithësi karakterizohet nga një traditë materialiste. Kështu, Chebyshev theksoi qartë rëndësinë vendimtare të praktikës, dhe Lyapunov shprehu stilin e shkollës matematikore ruse me fjalët e mëposhtme të mrekullueshme: "Zhvillimi i detajuar i pyetjeve që janë veçanërisht të rëndësishme nga pikëpamja e aplikimit dhe në të njëjtën kohë duke paraqitur të veçanta vështirësi teorike, që kërkojnë shpikjen e metodave të reja dhe një ngjitje në parimet e shkencës, pastaj përgjithësimin e gjetjeve dhe duke krijuar kështu një teori pak a shumë të përgjithshme." Përgjithësimet dhe abstraksionet nuk janë në vetvete, por në lidhje me një material specifik

Teoremat dhe teoritë jo në vetvete, por në lidhjen e përgjithshme të shkencës, duke çuar në fund të fundit në praktikë - kjo është ajo që rezulton të jetë në të vërtetë e rëndësishme dhe premtuese.

Këto ishin gjithashtu aspiratat e shkencëtarëve të tillë të mëdhenj si Gauss dhe Riemann.

Sidoqoftë, me zhvillimin e kapitalizmit në Evropë, pikëpamjet materialiste, të cilat pasqyronin ideologjinë e përparuar të borgjezisë në rritje të shekullit të 16-të - fillimi i shekullit të 19-të, filluan të zëvendësohen nga pikëpamje idealiste. Për shembull, Cantor (1846-1918), kur krijoi teorinë e grupeve të pafundme, iu referua drejtpërdrejt Zotit, duke folur në frymën se grupet e pafundme kanë ekzistencë absolute në mendjen hyjnore. Matematikani më i madh francez i fundit të shekullit të 19-të dhe fillimit të shekullit të 20-të. Poincaré parashtroi konceptin idealist të "konvencionalizmit", sipas të cilit matematika është një skemë e marrëveshjeve konvencionale të miratuara për lehtësinë e përshkrimit të shumëllojshmërisë së përvojës. Kështu, sipas Poincare-së, aksiomat e gjeometrisë Euklidiane nuk janë gjë tjetër veçse marrëveshje të kushtëzuara dhe kuptimi i tyre përcaktohet nga komoditeti dhe thjeshtësia, por jo nga korrespondenca e tyre me realitetin. Prandaj, Poincaré tha se, për shembull, në fizikë ata më mirë do të braktisnin ligjin e përhapjes drejtvizore të dritës sesa gjeometrinë Euklidiane. Ky këndvështrim u hodh poshtë nga zhvillimi i teorisë së relativitetit, e cila, me gjithë "thjeshtësinë" dhe "komoditetin" e gjeometrisë Euklidiane, në përputhje të plotë me idetë materialiste të Lobachevsky dhe Riemann, çoi në përfundimin se real gjeometria e hapësirës është e ndryshme nga ajo euklidiane.

Për shkak të vështirësive që u shfaqën në teorinë e grupeve dhe në lidhje me nevojën për të analizuar konceptet themelore të matematikës, midis matematikanëve në fillim të shekullit të 20-të. u shfaqën rryma të ndryshme. Uniteti në kuptimin e përmbajtjes së matematikës humbi; Matematikanë të ndryshëm filluan të shohin ndryshe jo vetëm bazat e përgjithshme të shkencës, siç ishte rasti më parë, por madje filluan të vlerësojnë ndryshe kuptimin dhe rëndësinë e rezultateve dhe provave specifike individuale. Përfundimet që disave u dukeshin kuptimplotë dhe kuptimplotë u shpallën pa kuptim dhe rëndësi nga të tjerët. U ngritën lëvizje idealiste të “logjikizmit”, “intuitizmit”, “formalizmit” etj.

Logjistikët pretendojnë se e gjithë matematika është e deduktueshme nga konceptet e logjikës. Intuitivistët e shohin burimin e matematikës në intuitë dhe i japin kuptim vetëm asaj që perceptohet në mënyrë intuitive. Prandaj, në veçanti, ata mohojnë plotësisht rëndësinë e teorisë së grupeve të pafundme të Cantor-it. Për më tepër, intuitivistët mohojnë kuptimin e thjeshtë edhe të deklaratave të tilla

si teoremë që çdo ekuacion algjebrik i shkallës ka rrënjë. Për ta, kjo deklaratë është bosh derisa të specifikohet një metodë për llogaritjen e rrënjëve. Kështu, mohimi i plotë i kuptimit objektiv të matematikës i bëri intuitivistët të diskreditonin një pjesë të rëndësishme të arritjeve të matematikës si "të pa kuptim". Më ekstremi prej tyre shkoi aq larg sa të pohonte se ka po aq matematikanë sa ka matematikanë.

Një përpjekje në mënyrën e tij për të shpëtuar matematikën nga ky lloj sulmi u bë nga matematikani më i madh i fillimit të shekullit tonë - D. Hilbert. Thelbi i idesë së tij ishte të reduktonte teoritë matematikore në operacione thjesht formale mbi simbolet sipas rregullave të përcaktuara. Llogaritja ishte se me një qasje kaq formale do të hiqeshin të gjitha vështirësitë, sepse lënda e matematikës do të ishin simbolet dhe rregullat për të vepruar me to pa asnjë lidhje me kuptimin e tyre. Ky është përcaktimi i formalizmit në matematikë. Sipas intuitionistit Brouwer, për formalistin e vërteta e matematikës është në letër, ndërsa për intuicionin është në kokën e matematikanit.

Megjithatë, nuk është e vështirë të shohësh se të dyja janë të gabuara, për matematikën, dhe në të njëjtën kohë ajo që është shkruar në letër dhe ajo që mendon matematikani, pasqyron realitetin dhe e vërteta e matematikës qëndron në korrespondencën e saj me realitetin objektiv. . Duke e ndarë matematikën nga realiteti material, të gjitha këto prirje rezultojnë të jenë idealiste.

Ideja e Hilbertit u mposht nga vetë zhvillimi i saj. Matematikani austriak Gödel vërtetoi se as aritmetika nuk mund të zyrtarizohet plotësisht, siç kishte shpresuar Hilberti. Përfundimi i Gödel zbuloi qartë dialektikën e brendshme të matematikës, e cila nuk lejon që asnjë nga fushat e saj të shterret nga llogaritja formale. Edhe pafundësia më e thjeshtë e një serie natyrore numrash doli të ishte një skemë e fundme e pashtershme e simboleve dhe rregullave për të vepruar me to. Kështu, u vërtetua matematikisht ajo që Engels shprehu në terma të përgjithshëm kur shkroi:

"Pafundësia është një kontradiktë... Shkatërrimi i kësaj kontradikte do të ishte fundi i pafundësisë." Hilberti shpresonte të mbyllte pafundësinë matematikore brenda kornizës së skemave të fundme dhe në këtë mënyrë të eliminonte të gjitha kontradiktat dhe vështirësitë. Kjo doli të ishte e pamundur.

Por në kushtet e kapitalizmit, konvencionalizmi, intuitizmi, formalizmi dhe lëvizje të tjera të ngjashme jo vetëm që ruhen, por plotësohen nga variante të reja të pikëpamjeve idealiste për matematikën. Teoritë që lidhen me analizën logjike të themeleve të matematikës përdoren ndjeshëm në disa variante të reja të idealizmit subjektiv. Subjektive

idealizmi tani përdor matematikën, në veçanti logjikën matematikore, jo më pak se fizikën, dhe për këtë arsye pyetjet e të kuptuarit të themeleve të matematikës bëhen veçanërisht të mprehta.

Kështu, vështirësitë në zhvillimin e matematikës në kushtet e kapitalizmit shkaktuan një krizë ideologjike të kësaj shkence, e ngjashme në themelet e saj me krizën e fizikës, thelbin e së cilës u sqarua nga Lenini në veprën e tij të shkëlqyer "Materializmi dhe Empirio". - Kritika.” Kjo krizë nuk do të thotë aspak se matematika në vendet kapitaliste është plotësisht e vonuar në zhvillimin e saj. Një numër shkencëtarësh me pozicione qartësisht idealiste po bëjnë suksese të rëndësishme, ndonjëherë të jashtëzakonshme, në zgjidhjen e problemeve specifike matematikore dhe zhvillimin e teorive të reja. Mjafton t'i referohemi zhvillimit të shkëlqyer të logjikës matematikore.

E meta themelore e pikëpamjes së matematikës, e përhapur gjerësisht në vendet kapitaliste, qëndron në idealizmin dhe metafizikën e saj: ndarja e matematikës nga realiteti dhe neglizhenca e zhvillimit të saj real. Logjistika, intuitizmi, formalizmi dhe tendenca të tjera të ngjashme nxjerrin në pah në matematikë një nga aspektet e saj - lidhjen me logjikën, qartësinë intuitive, ashpërsinë formale, etj. - ato ekzagjerojnë në mënyrë të paarsyeshme, absolutizojnë kuptimin e saj, e ndajnë atë nga realiteti dhe, pas një analize të thellë të kësaj. Një veçori e matematikës në vetvete është e humbur nga vështrimi i matematikës në tërësi. Është pikërisht për shkak të kësaj njëanshmërie që asnjë nga këto rryma, me gjithë hollësinë dhe thellësinë e përfundimeve individuale, nuk mund të çojë në një kuptim të saktë të matematikës. Në ndryshim nga rrymat dhe nuancat e ndryshme të idealizmit dhe metafizikës, materializmi dialektik e konsideron matematikën, si gjithë shkencën në tërësi, ashtu siç është, në të gjithë pasurinë dhe kompleksitetin e lidhjeve dhe zhvillimit të saj. Dhe pikërisht sepse materializmi dialektik përpiqet të kuptojë gjithë pasurinë dhe gjithë kompleksitetin e lidhjeve midis shkencës dhe realitetit, gjithë kompleksitetin e zhvillimit të saj, duke kaluar nga një përgjithësim i thjeshtë i përvojës në abstraksione më të larta dhe prej tyre në praktikë, pikërisht sepse vazhdimisht e drejton vetë qasjen e saj ndaj shkencës në përputhje me përmbajtjen e saj objektive, me zbulimet e saj të reja, është pikërisht për këtë arsye dhe, në fund të fundit, vetëm për këtë arsye, ajo rezulton të jetë e vetmja filozofi vërtet shkencore që çon në një kuptim të saktë të shkencës. në përgjithësi dhe në veçanti matematika.