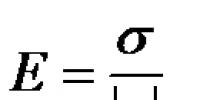Cili është kufiri i zeros? Zgjidhja e problemeve në gjetjen e mostrës së kufijve

Zgjidhje kufijtë e funksionit në internet. Gjeni vlerën kufizuese të një funksioni ose sekuence funksionale në një pikë, llogarisni përfundimtare vlera e funksionit në pafundësi. përcaktimi i konvergjencës së një serie numrash dhe shumë më tepër mund të bëhet falë shërbimit tonë në internet -. Ne ju lejojmë të gjeni kufijtë e funksioneve në internet shpejt dhe saktë. Ju vetë futni variablin e funksionit dhe kufirin në të cilin priret dhe shërbimi ynë kryen të gjitha llogaritjet për ju, duke dhënë një përgjigje të saktë dhe të thjeshtë. Dhe për gjetja e kufirit në internet mund të futni si seritë numerike ashtu edhe funksionet analitike që përmbajnë konstante në shprehjen e mirëfilltë. Në këtë rast, kufiri i gjetur i funksionit do të përmbajë këto konstante si argumente konstante në shprehje. Shërbimi ynë zgjidh çdo problem kompleks të gjetjes kufijtë online, mjafton të tregohet funksioni dhe pika në të cilën është e nevojshme të llogaritet vlera kufi e funksionit. Duke llogaritur kufijtë online, mund të përdorni metoda dhe rregulla të ndryshme për zgjidhjen e tyre, duke kontrolluar rezultatin e marrë me zgjidhja e kufijve në internet në faqen www.site, e cila do të çojë në përfundimin e suksesshëm të detyrës - ju do të shmangni gabimet tuaja dhe gabimet klerikale. Ose mund të na besoni plotësisht dhe të përdorni rezultatin tonë në punën tuaj, pa shpenzuar përpjekje dhe kohë shtesë për të llogaritur në mënyrë të pavarur kufirin e funksionit. Ne lejojmë futjen e vlerave kufitare të tilla si pafundësia. Është e nevojshme të futni një anëtar të përbashkët të një sekuence numrash dhe www.site do të llogarisë vlerën limit online në pafundësi plus ose minus.

Një nga konceptet bazë të analizës matematikore është kufiri i funksionit Dhe kufiri i sekuencës në një pikë dhe në pafundësi, është e rëndësishme të jesh në gjendje të zgjidhësh saktë kufijtë. Me shërbimin tonë kjo nuk do të jetë e vështirë. Është marrë një vendim kufijtë online brenda pak sekondash, përgjigja është e saktë dhe e plotë. Studimi i analizës matematikore fillon me kalimi në kufi, kufijtë përdoren pothuajse në të gjitha fushat e matematikës së lartë, kështu që është e dobishme të keni një server në dorë zgjidhje kufitare në internet, që është matematikam.ru.

Kur llogaritni kufijtë, duhet të keni parasysh rregullat themelore të mëposhtme:

1. Kufiri i shumës (diferencës) i funksioneve është i barabartë me shumën (diferencën) e kufijve të termave:

2. Kufiri i prodhimit të funksioneve është i barabartë me produktin e kufijve të faktorëve:

3. Kufiri i raportit të dy funksioneve është i barabartë me raportin e kufijve të këtyre funksioneve:

.

4. Faktori konstant mund të merret përtej shenjës kufitare:

.

5. Kufiri i një konstante është i barabartë me vetë konstanten:

6. Për funksionet e vazhdueshme, simbolet e kufirit dhe funksionit mund të ndërrohen:

.

Gjetja e kufirit të një funksioni duhet të fillojë duke zëvendësuar vlerën në shprehjen e funksionit. Për më tepër, nëse fitohet vlera numerike 0 ose ¥, atëherë është gjetur kufiri i dëshiruar.

Shembulli 2.1. Llogaritni kufirin.

Zgjidhje.

.

Shprehjet e formës , , , , , quhen pasiguritë.

Nëse merrni një pasiguri të formës, atëherë për të gjetur kufirin duhet të transformoni funksionin në mënyrë që të zbuloni këtë pasiguri.

Pasiguria e formës zakonisht fitohet kur jepet kufiri i raportit të dy polinomeve. Në këtë rast, për të llogaritur kufirin, rekomandohet faktorizimi i polinomeve dhe zvogëlimi i tyre me një faktor të përbashkët. Ky shumëzues është zero në vlerën kufi X .

Shembulli 2.2. Llogaritni kufirin.

Zgjidhje.

Duke zëvendësuar , marrim pasiguri:

.

Le të faktorizojmë numëruesin dhe emëruesin:

;

Le të reduktojmë me një faktor të përbashkët dhe të marrim

.

Një pasiguri e formës fitohet kur kufiri i raportit të dy polinomeve është dhënë në . Në këtë rast, për ta llogaritur atë, rekomandohet të ndahen të dy polinomet me X në gradën e lartë.

Shembulli 2.3. Llogaritni kufirin.

Zgjidhje. Kur zëvendësojmë ∞, marrim një pasiguri të formës , kështu që i ndajmë të gjitha termat e shprehjes me x 3.

.

Këtu merret parasysh se.

Kur llogaritni kufijtë e një funksioni që përmban rrënjë, rekomandohet të shumëzoni dhe ndani funksionin me konjugatin e tij.

Shembulli 2.4. Llogaritni kufirin

Zgjidhje.

Kur llogariten kufijtë për të zbuluar pasigurinë e formës ose (1) ∞, shpesh përdoren kufijtë e parë dhe të dytë të shquar:

Shumë probleme që lidhen me rritjen e vazhdueshme të një sasie çojnë në kufirin e dytë të jashtëzakonshëm.

Le të shqyrtojmë shembullin e Ya. I. Perelman, duke dhënë një interpretim të numrit e në problemin e interesit të përbërë. Në bankat e kursimeve, paratë e interesit i shtohen kapitalit fiks çdo vit. Nëse aderimi bëhet më shpesh, atëherë kapitali rritet më shpejt, pasi një sasi më e madhe përfshihet në formimin e interesit. Le të marrim një shembull thjesht teorik, shumë të thjeshtuar.

Le të depozitohen 100 deniera në bankë. njësive bazuar në 100% në vit. Nëse paratë e interesit i shtohen kapitalit fiks vetëm pas një viti, atëherë deri në këtë periudhë 100 den. njësive do të kthehet në 200 njësi monetare.

Tani le të shohim se në çfarë do të kthehen 100 denize. njësi, nëse paratë e interesit i shtohen kapitalit fiks çdo gjashtë muaj. Pas gjashtë muajsh, 100 den. njësive do të rritet me 100 × 1,5 = 150, dhe pas gjashtë muajsh të tjerë - me 150 × 1,5 = 225 (den. njësi). Nëse aderimi bëhet çdo 1/3 e vitit, atëherë pas një viti 100 den. njësive do të kthehet në 100 × (1 +1/3) 3 "237 (den. njësi).

Ne do të rrisim kushtet për shtimin e parave të interesit në 0,1 vit, në 0,01 vit, në 0,001 vit, etj. Pastaj nga 100 den. njësive pas një viti do të jetë:

100 × (1 +1/10) 10 » 259 (den. njësi),

100 × (1+1/100) 100 » 270 (den. njësi),

100 × (1+1/1000) 1000 » 271 (den. njësi).

Me një ulje të pakufizuar të kushteve për shtimin e interesit, kapitali i akumuluar nuk rritet pafundësisht, por i afrohet një kufiri të caktuar të barabartë me afërsisht 271. Kapitali i depozituar me 100% në vit nuk mund të rritet më shumë se 2,71 herë, edhe nëse interesi i përllogaritur. i shtoheshin kryeqytetit çdo sekondë sepse

Shembulli 2.5. Llogaritni kufirin e një funksioni

Zgjidhje.

Shembulli 2.6. Llogaritni kufirin e një funksioni .

Zgjidhje. Duke zëvendësuar marrim pasigurinë:

.

Duke përdorur formulën trigonometrike, ne e transformojmë numëruesin në një produkt:

Si rezultat marrim

Këtu merret parasysh kufiri i dytë i shquar.

Shembulli 2.7. Llogaritni kufirin e një funksioni

Zgjidhje.

.

Për të zbuluar pasigurinë e formës ose, mund të përdorni rregullin e L'Hopital, i cili bazohet në teoremën e mëposhtme.

Teorema. Kufiri i raportit të dy funksioneve pafundësisht të vogla ose pafundësisht të mëdha është i barabartë me kufirin e raportit të derivateve të tyre

Vini re se ky rregull mund të zbatohet disa herë radhazi.

Shembulli 2.8. Gjej

Zgjidhje. Gjatë zëvendësimit kemi një pasiguri të formës . Duke zbatuar rregullin e L'Hopital, ne marrim

Vazhdimësia e funksionit

Një veti e rëndësishme e një funksioni është vazhdimësia.

Përkufizimi. Funksioni merret parasysh të vazhdueshme, nëse një ndryshim i vogël në vlerën e argumentit sjell një ndryshim të vogël në vlerën e funksionit.

Matematikisht kjo shkruhet si më poshtë: kur

Me dhe nënkuptohet rritja e variablave, pra diferenca midis vlerave pasuese dhe atyre të mëparshme: , (Figura 2.3)

Figura 2.3 – Rritja e variablave

Nga përkufizimi i një funksioni të vazhdueshëm në pikën rrjedh se . Kjo barazi do të thotë se plotësohen tre kushte:

Zgjidhje. Për funksionin pika është e dyshimtë për një ndërprerje, le ta kontrollojmë këtë dhe të gjejmë kufij të njëanshëm

Prandaj, , Do të thotë - pikë pushimi

Derivat i një funksioni

Kufiri i funksionit- numri a do të jetë kufiri i një sasie të ndryshueshme nëse, në procesin e ndryshimit të saj, kjo sasi e ndryshueshme afrohet në mënyrë të pacaktuar a.

Ose me fjalë të tjera, numri Aështë kufiri i funksionit y = f(x) në pikën x 0, nëse për ndonjë sekuencë pikash nga fusha e përcaktimit të funksionit , jo e barabartë x 0, dhe që konvergon në pikën x 0 (lim x n = x0), sekuenca e vlerave përkatëse të funksionit konvergon me numrin A.

Grafiku i një funksioni, kufiri i të cilit, duke pasur parasysh një argument që priret në pafundësi, është i barabartë me L:

Kuptimi Aështë limit (vlera kufi) e funksionit f(x) në pikën x 0 në rast të ndonjë sekuence pikash , e cila konvergon në x 0, por që nuk përmban x 0 si një nga elementët e tij (d.m.th. në afërsi të shpuar x 0), sekuenca e vlerave të funksionit konvergon në A.

Kufiri i një funksioni Cauchy.

Kuptimi A do të jetë kufiri i funksionit f(x) në pikën x 0 nëse për ndonjë numër jo negativ të marrë paraprakisht ε do të gjendet numri përkatës jo negativ δ = δ(ε) të tilla që për çdo argument x, duke plotesuar kushtin 0 < | x - x0 | < δ , pabarazia do të plotësohet | f(x)A |< ε .

Do të jetë shumë e thjeshtë nëse e kuptoni thelbin e kufirit dhe rregullat themelore për gjetjen e tij. Cili është kufiri i funksionit f (x) në x duke u përpjekur për a barazohet A, shkruhet kështu:

Për më tepër, vlera drejt së cilës priret ndryshorja x, mund të jetë jo vetëm një numër, por edhe pafundësi (∞), ndonjëherë +∞ ose -∞, ose mund të mos ketë fare kufi.

Për të kuptuar se si gjeni kufijtë e një funksioni, është më mirë të shikoni shembuj zgjidhjesh.

Është e nevojshme të gjenden kufijtë e funksionit f (x) = 1/x në:

x→ 2, x→ 0, x→ ∞.

Le të gjejmë një zgjidhje për kufirin e parë. Për ta bërë këtë, thjesht mund të zëvendësoni x numri për të cilin priret, d.m.th. 2, marrim:

Le të gjejmë kufirin e dytë të funksionit. Këtu zëvendësoni 0 të pastër në vend xështë e pamundur, sepse Ju nuk mund të pjesëtoni me 0. Por ne mund të marrim vlera afër zeros, për shembull, 0.01; 0,001; 0.0001; 0.00001 e kështu me radhë, dhe vlera e funksionit f (x) do të rritet: 100; 1000; 10000; 100,000 e kështu me radhë. Kështu, mund të kuptohet se kur x→ 0 vlera e funksionit që është nën shenjën limit do të rritet pa limit, d.m.th. përpiqen drejt pafundësisë. Që do të thotë:

Në lidhje me kufirin e tretë. E njëjta situatë si në rastin e mëparshëm, është e pamundur të zëvendësohet ∞ në formën e tij më të pastër. Duhet të shqyrtojmë rastin e rritjes së pakufizuar x. Ne zëvendësojmë 1000 një nga një; 10000; 100000 e kështu me radhë, kemi atë vlerën e funksionit f (x) = 1/x do të ulet: 0,001; 0.0001; 0.00001; dhe kështu me radhë, duke u prirur në zero. Kjo është arsyeja pse:

Është e nevojshme të llogaritet kufiri i funksionit

Duke filluar të zgjidhim shembullin e dytë, shohim pasiguri. Nga këtu gjejmë shkallën më të lartë të numëruesit dhe emëruesit - kjo është x 3, e nxjerrim nga kllapat në numërues dhe emërues dhe më pas e zvogëlojmë me:

Përgjigju

Hapi i parë në duke gjetur këtë kufi, zëvendësoni vlerën 1 në vend të kësaj x, duke rezultuar në pasiguri. Për ta zgjidhur atë, le të faktorizojmë numëruesin dhe ta bëjmë këtë duke përdorur metodën e gjetjes së rrënjëve të një ekuacioni kuadratik x 2 + 2x - 3:

D = 2 2 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ x 1 = -3;x 2= 1.

Pra, numëruesi do të jetë:

Përgjigju

Ky është përkufizimi i vlerës së tij specifike ose një zone të caktuar ku bie funksioni, i cili kufizohet nga kufiri.

Për të zgjidhur kufijtë, ndiqni rregullat:

Duke kuptuar thelbin dhe kryesorin rregullat për zgjidhjen e limitit, do të merrni një kuptim bazë se si t'i zgjidhni ato.

Konceptet e kufijve të sekuencave dhe funksioneve. Kur është e nevojshme të gjendet kufiri i një sekuence, ai shkruhet si më poshtë: lim xn=a. Në një sekuencë të tillë sekuencash, xn priret në a dhe n priret në pafundësi. Sekuenca zakonisht përfaqësohet si një seri, për shembull:
x1, x2, x3...,xm,...,xn... .
Sekuencat ndahen në rritëse dhe zvogëluese. Për shembull:
xn=n^2 - sekuenca në rritje
yn=1/n - sekuencë
Kështu, për shembull, kufiri i sekuencës xn=1/n^:
lim 1/n^2=0

x→∞
Ky kufi është i barabartë me zero, pasi n→∞, dhe sekuenca 1/n^2 tenton në zero.

Në mënyrë tipike, një sasi e ndryshueshme x tenton në një kufi të fundëm a, dhe x vazhdimisht i afrohet a-së dhe sasia a është konstante. Kjo shkruhet si më poshtë: limx =a, ndërsa n gjithashtu mund të priret në zero ose në pafundësi. Ka funksione të pafundme, për të cilat kufiri priret në pafundësi. Në raste të tjera, kur, për shembull, funksioni po ngadalëson një tren, është e mundur që kufiri të priret në zero.
Kufijtë kanë një sërë pronash. Në mënyrë tipike, çdo funksion ka vetëm një kufi. Kjo është vetia kryesore e limitit. Pronat e tjera të tyre janë renditur më poshtë:
* Kufiri i shumës është i barabartë me shumën e limiteve:
lim(x+y)=lim x+lim y
* Kufiri i produktit është i barabartë me produktin e kufijve:
lim(xy)=lim x*lim y
* Kufiri i herësit është i barabartë me herësin e kufijve:
lim(x/y)=lim x/lim y
* Faktori konstant merret jashtë shenjës kufitare:
lim(Cx)=C lim x
Jepet një funksion 1 /x në të cilin x →∞, kufiri i tij është zero. Nëse x→0, kufiri i një funksioni të tillë është ∞.
Ekzistojnë përjashtime nga këto rregulla për funksionet trigonometrike. Meqenëse funksioni sin x tenton gjithmonë në unitet kur i afrohet zeros, identiteti qëndron për të:
lim sin x/x=1

Në një numër problemesh ka funksione, kur llogariten kufijtë e të cilave lind pasiguria - një situatë në të cilën kufiri nuk mund të llogaritet. E vetmja rrugëdalje nga kjo situatë është zbatimi i rregullit të L'Hopital. Ekzistojnë dy lloje të pasigurive:
* pasiguria e formës 0/0
* pasiguria e formës ∞/∞
Për shembull, jepet një kufi i formës së mëposhtme: lim f(x)/l(x) dhe f(x0)=l(x0)=0. Në këtë rast, lind një pasiguri e formës 0/0. Për të zgjidhur një problem të tillë, të dy funksionet diferencohen, pas së cilës gjendet kufiri i rezultatit. Për pasiguritë e tipit 0/0, kufiri është:
lim f(x)/l(x)=lim f"(x)/l"(x) (në x→0)
I njëjti rregull vlen edhe për pasiguritë e tipit ∞/∞. Por në këtë rast barazia e mëposhtme është e vërtetë: f(x)=l(x)=∞
Duke përdorur rregullin e L'Hopital, mund të gjeni vlerat e çdo kufiri në të cilin shfaqen pasiguritë. Një parakusht për

vëllimi - nuk ka gabime gjatë gjetjes së derivateve. Pra, për shembull, derivati ​​i funksionit (x^2)" është i barabartë me 2x. Nga këtu mund të konkludojmë se:
f"(x)=nx^(n-1)

Për ata që duan të mësojnë se si të gjejnë kufizime, në këtë artikull do t'ju tregojmë për këtë. Ne nuk do të thellohemi në teori; mësuesit zakonisht e japin atë në leksione. Pra, "teoria e mërzitshme" duhet të shënohet në fletoret tuaja. Nëse nuk është kështu, atëherë mund të lexoni tekste shkollore të marra nga biblioteka e institucionit arsimor ose nga burime të tjera të internetit.

Pra, koncepti i kufirit është mjaft i rëndësishëm në studimin e matematikës së lartë, veçanërisht kur hasni në llogaritjen integrale dhe kuptoni lidhjen midis kufirit dhe integralit. Materiali aktual do të shikojë shembuj të thjeshtë, si dhe mënyra për t'i zgjidhur ato.

Shembuj zgjidhjesh

Shembulli 1

Llogaritni a) $ \lim_(x \to 0) \frac(1)(x) $; b)$ \lim_(x \në \infty) \frac(1)(x) $

Zgjidhje

a) $$ \lim \limits_(x \në 0) \frac(1)(x) = \infty $$ b)$$ \lim_(x \to \infty) \frac(1)(x) = 0 $$ Njerëzit shpesh na dërgojnë këto kufizime me një kërkesë për të ndihmuar në zgjidhjen e tyre. Ne vendosëm t'i theksojmë ato si një shembull më vete dhe të shpjegojmë se këto kufij thjesht duhet të mbahen mend, si rregull. Nëse nuk mund ta zgjidhni problemin tuaj, atëherë na dërgoni atë. Ne do të ofrojmë zgjidhje të detajuar. Ju do të jeni në gjendje të shikoni ecurinë e llogaritjes dhe të merrni informacion. Kjo do t'ju ndihmojë të merrni notën tuaj nga mësuesi juaj në kohën e duhur!

Përgjigju

$$ \text(a)) \lim \limits_(x \to 0) \frac(1)(x) = \infty \text(b))\lim \limits_(x \to \infty) \frac(1 )(x) = 0 $$

Çfarë duhet bërë me pasigurinë e formës: $ \bigg [\frac(0)(0) \bigg ] $

Shembulli 3

Zgjidh $ \lim \limits_(x \në -1) \frac(x^2-1)(x+1) $

Zgjidhje

Si gjithmonë, ne fillojmë duke zëvendësuar vlerën $ x $ në shprehjen nën shenjën kufi. $$ \lim \limits_(x \ deri -1) \frac(x^2-1)(x+1) = \frac((-1)^2-1)(-1+1)=\frac( 0) (0) $$ Çfarë është më pas tani? Çfarë duhet të ndodhë në fund? Meqenëse kjo është pasiguri, kjo nuk është ende një përgjigje dhe ne vazhdojmë llogaritjen. Meqenëse kemi një polinom në numërues, do ta faktorizojmë duke përdorur formulën e njohur për të gjithë nga shkolla $$ a^2-b^2=(a-b)(a+b) $$. Të kujtohet? E madhe! Tani vazhdo dhe përdore me këngën :) Gjejmë se numëruesi $ x^2-1=(x-1)(x+1) $ Ne vazhdojmë të zgjidhim duke marrë parasysh transformimin e mësipërm: $$ \lim \limits_(x \deri -1)\frac(x^2-1)(x+1) = \lim \limits_(x \to -1)\frac((x-1)(x+ 1 ))(x+1) = $$ $$ = \lim \limits_(x \në -1)(x-1)=-1-1=-2 $$

Përgjigju

$$ \lim \limits_(x \në -1) \frac(x^2-1)(x+1) = -2 $$

Le ta shtyjmë kufirin në dy shembujt e fundit në pafundësi dhe të marrim parasysh pasigurinë: $ \bigg [\frac(\infty)(\infty) \bigg ] $

Shembulli 5

Llogarit $ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) $

Zgjidhje

$ \lim \limits_(x \në \infty) \frac(x^2-1)(x+1) = \frac(\infty)(\infty) $ Çfarë duhet bërë? Cfare duhet te bej? Mos u frikësoni, sepse e pamundura është e mundur. Është e nevojshme të hiqni x si në numërues ashtu edhe në emërues, dhe pastaj ta zvogëloni atë. Pas kësaj, përpiquni të llogarisni kufirin. Le te perpiqemi... $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) =\lim \limits_(x \to \infty) \frac(x^2(1-\frac (1)(x^2)))(x(1+\frac(1)(x))) = $$ $$ = \lim \limits_(x \në \infty) \frac(x(1-\frac(1)(x^2)))((1+\frac(1)(x))) = $$ Duke përdorur përkufizimin nga Shembulli 2 dhe duke zëvendësuar pafundësinë me x, marrim: $$ = \frac(\infty(1-\frac(1)(\infty)))((1+\frac(1)(\infty))) = \frac(\infty \cdot 1)(1+ 0) = \frac(\infty)(1) = \infty $$

Përgjigju

$$ \lim \limits_(x \në \infty) \frac(x^2-1)(x+1) = \infty $$

Algoritmi për llogaritjen e limiteve

Pra, le të përmbledhim shkurtimisht shembujt dhe të krijojmë një algoritëm për zgjidhjen e kufijve:

1. Zëvendësoni pikën x në shprehjen pas shenjës kufitare. Nëse fitohet një numër ose pafundësi e caktuar, atëherë kufiri zgjidhet plotësisht. Përndryshe, kemi pasiguri: “zero pjesëtuar me zero” ose “pafundësi pjesëtuar me pafundësi” dhe kalojmë në hapat e mëtejshëm të udhëzimeve.
2. Për të eliminuar pasigurinë e "zeros pjesëtuar me zero", duhet të faktorizoni numëruesin dhe emëruesin. Zvogëloni të ngjashmet. Zëvendësoni pikën x në shprehjen nën shenjën e kufirit.
3. Nëse pasiguria është "pafundësia e ndarë me pafundësinë", atëherë ne nxjerrim si numëruesin ashtu edhe emëruesin x në shkallën më të madhe. Ne shkurtojmë X-të. Ne zëvendësojmë vlerat e x nga poshtë kufirit në shprehjen e mbetur.

Në këtë artikull, ju mësuat bazat e zgjidhjes së kufijve, të përdorura shpesh në kursin Calculus. Sigurisht, këto nuk janë të gjitha llojet e problemeve të ofruara nga ekzaminuesit, por vetëm kufijtë më të thjeshtë. Ne do të flasim për lloje të tjera detyrash në artikujt e ardhshëm, por së pari ju duhet të mësoni këtë mësim në mënyrë që të ecni përpara. Le të diskutojmë se çfarë të bëjmë nëse ka rrënjë, gradë, të studiojmë funksione ekuivalente pafundësisht të vogla, kufij të mrekullueshëm, rregullin e L'Hopital.

Nëse nuk mund t'i kuptoni vetë kufijtë, mos u frikësoni. Ne jemi gjithmonë të lumtur të ndihmojmë!