Produkt skalar vektorët (më tej të referuar si SP). Te dashur miq! Provimi i matematikës përfshin një grup problemesh për zgjidhjen e vektorëve. Ne kemi shqyrtuar tashmë disa probleme. Mund t'i shihni në kategorinë "Vektorë". Në përgjithësi, teoria e vektorëve nuk është e ndërlikuar, gjëja kryesore është ta studiojmë atë vazhdimisht. Llogaritjet dhe operacionet me vektorë në kursi shkollor Matematika është e thjeshtë, formulat nuk janë të komplikuara. Hidhini një sy. Në këtë artikull do të analizojmë problemet mbi SP të vektorëve (të përfshirë në Provimin e Unifikuar të Shtetit). Tani "zhytja" në teori:

H Për të gjetur koordinatat e një vektori, duhet të zbrisni nga koordinatat e fundit të tijkoordinatat përkatëse të origjinës së tij

Dhe më tej:

*Gjatësia e vektorit (moduli) përcaktohet si më poshtë:

Këto formula duhen mbajtur mend!!!

Le të tregojmë këndin midis vektorëve:

Është e qartë se mund të ndryshojë nga 0 në 180 0(ose në radianë nga 0 në Pi).

Mund të nxjerrim disa përfundime për shenjën e produktit skalar. Gjatësitë e vektorëve kanë një vlerë pozitive, kjo është e qartë. Kjo do të thotë se shenja e produktit skalar varet nga vlera e kosinusit të këndit ndërmjet vektorëve.

Rastet e mundshme:

1. Nëse këndi ndërmjet vektorëve është akut (nga 0 0 në 90 0), atëherë kosinusi i këndit do të ketë vlerë pozitive.

2. Nëse këndi ndërmjet vektorëve është i mpirë (nga 90 0 në 180 0), atëherë kosinusi i këndit do të ketë vlerë negative.

*Në gradë zero, pra kur vektorët kanë të njëjtin drejtim, kosinus e barabartë me një dhe në përputhje me rrethanat rezultati do të jetë pozitiv.

Në 180 o, domethënë kur vektorët kanë drejtime të kundërta, kosinusi është i barabartë me minus një,dhe rrjedhimisht rezultati do të jetë negativ.

Tani PIKA E RËNDËSISHME!

Në 90 o, domethënë kur vektorët janë pingul me njëri-tjetrin, kosinusi e barabartë me zero, dhe për këtë arsye SP është e barabartë me zero. Ky fakt (pasojë, përfundim) përdoret në zgjidhjen e shumë problemeve ku bëhet fjalë për pozicionin relativ të vektorëve, përfshirë në problemet e përfshira në bankë e hapur detyra matematike.

Le të formulojmë pohimin: produkti skalar është i barabartë me zero nëse dhe vetëm nëse këta vektorë shtrihen në vija pingule.

Pra, formulat për vektorët SP:

Nëse dihen koordinatat e vektorëve ose koordinatat e pikave të fillimit dhe mbarimit të tyre, atëherë gjithmonë mund të gjejmë këndin midis vektorëve:

Le të shqyrtojmë detyrat:

27724 Gjeni prodhimin skalar të vektorëve a dhe b.

Ne mund ta gjejmë produktin skalar të vektorëve duke përdorur një nga dy formulat:

Këndi ndërmjet vektorëve është i panjohur, por ne mund të gjejmë lehtësisht koordinatat e vektorëve dhe më pas të përdorim formulën e parë. Meqenëse origjina e të dy vektorëve përputhet me origjinën e koordinatave, koordinatat e këtyre vektorëve janë të barabarta me koordinatat e skajeve të tyre, d.m.th.

Si të gjeni koordinatat e një vektori përshkruhet në.

Ne llogarisim:

Përgjigje: 40

Le të gjejmë koordinatat e vektorëve dhe të përdorim formulën:

Për të gjetur koordinatat e një vektori, është e nevojshme të zbriten koordinatat përkatëse të fillimit të tij nga koordinatat e fundit të vektorit, që do të thotë

Ne llogarisim produktin skalar:

Përgjigje: 40

Gjeni këndin midis vektorëve a dhe b. Jepni përgjigjen tuaj në shkallë.

Lërini koordinatat e vektorëve të kenë formën:

Për të gjetur këndin ndërmjet vektorëve, ne përdorim formulën për produktin skalar të vektorëve:

Kosinusi i këndit ndërmjet vektorëve:

Prandaj:

Koordinatat e këtyre vektorëve janë të barabarta:

Le t'i zëvendësojmë ato në formulën:

Këndi ndërmjet vektorëve është 45 gradë.

Përgjigje: 45

1. Përkufizimi dhe vetitë më të thjeshta. Le të marrim vektorët jozero a dhe b dhe t'i vizatojmë nga një pikë arbitrare O: OA = a dhe OB = b. Madhësia e këndit AOB quhet kënd ndërmjet vektorëve a dhe b dhe shënohet (a,b). Nëse të paktën njëri nga dy vektorët është zero, atëherë këndi ndërmjet tyre, sipas përkufizimit, konsiderohet i drejtë. Vini re se sipas përkufizimit këndi ndërmjet vektorëve nuk është më i vogël se 0 dhe jo më shumë se . Për më tepër, këndi ndërmjet dy vektorëve jozero është i barabartë me 0 nëse dhe vetëm nëse këta vektorë janë në bashkëdrejtim dhe të barabartë me nëse dhe vetëm nëse janë në drejtime të kundërta.

Le të kontrollojmë që këndi ndërmjet vektorëve të mos varet nga zgjedhja e pikës O. Kjo është e qartë nëse vektorët janë kolinear. Përndryshe, ne do të shtyjmë nga një pikë arbitrare O 1 vektorët O 1 A 1 = a dhe O 1 NË 1 = b dhe vini re se trekëndëshat AOB dhe A 1 RRETH 1 NË 1 e barabartë në tre anët, sepse |OA| = |O 1 A 1 | = |a|, |OB| = |O 1 NË 1 | = |b|, |AB| = |A 1 NË 1 | = |b–a|. Prandaj, këndet AOB dhe A 1 RRETH 1 NË 1 janë të barabartë.

Tani mund të japim pikën kryesore në këtë paragraf

(5.1) Përkufizim. Prodhimi skalar i dy vektorëve a dhe b (shënohet ab) është numri 6 , e barabartë me prodhimin e gjatësive të këtyre vektorëve dhe kosinusit të këndit ndërmjet vektorëve. Shkurtimisht:

ab = |a||b|ko (a,b).

Operacioni i gjetjes së një produkti skalar quhet shumëzim skalar i vektorit. Prodhimi skalar aa i një vektori me vetveten quhet katrori skalar i këtij vektori dhe shënohet një 2 .

(5.2) Katrori skalar i një vektori është i barabartë me katrorin e gjatësisë së tij.

 Nëse |a|  0, atëherë (a, a) = 0, nga ku a 2 = |a||a|cos0 = |a| 2 . Nëse a = 0, atëherë a 2 = |a| 2 = 0. 

(5.3) Pabarazia Cauchy. Moduli i prodhimit skalar të dy vektorëve nuk e kalon prodhimin e moduleve të faktorëve: |ab| |a||b|. Në këtë rast, barazia arrihet nëse dhe vetëm nëse vektorët a dhe b janë kolinear.

 Sipas përkufizimit |ab| = ||a||b|ko (a,b)| = |a||b||ko (a,b)|  |a||b. Kjo vërteton vetë pabarazinë e Cauchy. Tani le të vërejmë. se për vektorët jozero a dhe b barazia në të arrihet nëse dhe vetëm nëse |cos (a,b)| = 1, d.m.th. në (a,b) = 0 ose (a,b) =  . Kjo e fundit është ekuivalente me faktin që vektorët a dhe b janë të bashkëdrejtuar ose të drejtuar në të kundërt, d.m.th. kolineare. Nëse të paktën njëri nga vektorët a dhe b është zero, atëherë ata janë kolinear dhe |ab| = |a||b| = 0. 

2. Vetitë themelore të shumëzimit skalar. Këto përfshijnë sa vijon:

(SU1) ab = ba (komutativiteti);

(SU2) (xa)b = x(ab) (asociativiteti);

(SU3) a(b+c) = ab + ac (shpërndarja).

Komutativiteti këtu është i qartë, sepse ab =  ba. Asociativiteti në x = 0 është gjithashtu i dukshëm. Nëse x > 0, atëherë

(ha)b = |ha||b|ko (xa,b) = |x||a||b|kos (xa,b) = x|a||b|kos (a,b) = x(ab),

për (xa,b) = (a,b) (nga bashkëdrejtimi i vektorëve xa dhe a - Fig. 21). Nëse x< 0, atëherë

(xa)b = |x||a||b|kos (хa,b) = –х|а||b|(–cos (a,b)) = x|a||b|kos (a,b) = x(ab),

për (xa,b) = –  (a,b) (nga drejtimi i kundërt i vektorëve xa dhe a - Fig. 22). Kështu, dëshmohet edhe asociativiteti.

Provimi i shpërndarjes është më i vështirë. Për këtë na duhen të tilla

(5.4) Lemë. Le të jetë a një vektor jozero paralel me drejtëzën l dhe b një vektor arbitrar. Pastaj projeksioni ortogonalb" e vektorit b në drejtëzën l është e barabartë me
.



Nëse b = 0, atëherëb" = 0 dhe ab = 0, kështu që në këtë rast lema është e vërtetë. Në vijim do të supozojmë se vektori b" është jo zero. Në këtë rast, nga një pikë arbitrare O e drejtëzës l ne grafikojmë vektorët OA = a dhe OB = b, dhe gjithashtu ulim pingulin BB" nga pika B në drejtëzën l. Sipas përkufizimitOB" = b"Dhe (a,b) =  AOB. Le të shënojmë AOB nëpërmjet dhe provoni lemën veçmas për secilën nga tre rastet e mëposhtme:

1)  <  /2. Pastaj vektorët a dhe bashkëdrejtuar (Fig. 23) dhe

b" = =
=
.

2)  >  /2. Pastaj vektorët a dheb" janë të drejtuara në të kundërt (Fig. 24) dhe

b" = – = –
= .

3)  =  /2. Pastajb" = 0 dhe ab = 0, nga kub" =
= 0. 

Tani vërtetojmë shpërndarjen (SU3). Është e qartë nëse vektori a është zero. Le të a  0. Më pas vizatojmë vijën e drejtë l || a, dhe shënoni meb"Dhec"Projeksionet ortogonale të vektorëve b dhe c mbi të, dhe përmesd" – projeksion ortogonal vektorët d = b+c mbi të. Nga teorema 3.5d" = b"+ c"Duke zbatuar Lemën 5.4 në barazinë e fundit, marrim barazinë
=
. Duke e shumëzuar atë në shkallë me a, gjejmë se 2 =
, nga e cila ad = ab+ac, që është ajo që duhej vërtetuar.

Vetitë e shumëzimit skalar të vektorëve që kemi vërtetuar janë të ngjashme me vetitë përkatëse të shumëzimit të numrave. Por jo të gjitha vetitë e shumëzimit të numrave kalojnë në shumëzimin skalar të vektorëve. Këtu janë shembuj tipikë:

1

) Nëse ab = 0, atëherë kjo nuk do të thotë se a = 0 ose b = 0. Shembull: dy vektorë jo zero që formojnë një kënd të drejtë.

2) Nëse ab = ac, atëherë kjo nuk do të thotë se b = c, edhe nëse vektori a është jo zero. Shembull: b dhe c janë dy vektorë të ndryshëm me të njëjtën gjatësi, që formojnë kënde të barabarta me vektorin a (Fig. 25).

3) Nuk është e vërtetë që a(bc) = (ab)c është gjithmonë e vërtetë: nëse vetëm për shkak se vlefshmëria e një barazie të tillë për bc, ab 0 nënkupton kolinearitetin e vektorëve a dhe c.

3. Ortogonaliteti i vektorëve. Dy vektorë quhen ortogonalë nëse këndi ndërmjet tyre është i drejtë. Ortogonaliteti i vektorëve tregohet nga ikona .

Kur përcaktuam këndin midis vektorëve, ne ramë dakord që këndi midis vektorit zero dhe çdo vektori tjetër të ishte i drejtë. Prandaj, vektori zero është ortogonal me cilindo. Kjo marrëveshje na lejon ta vërtetojmë këtë

(5.5) Test për ortogonalitetin e dy vektorëve. Dy vektorë janë ortogonalë nëse dhe vetëm nëse produkti i tyre me pika është 0.

 Le të jenë a dhe b vektorë arbitrarë. Nëse të paktën njëri prej tyre është zero, atëherë ato janë ortogonale, dhe produkti i tyre skalar është i barabartë me 0. Kështu, në këtë rast teorema është e vërtetë. Le të supozojmë tani se të dy këta vektorë janë jo zero. Sipas përkufizimit ab = |a||b|cos (a,b). Meqenëse, sipas supozimit tonë, numrat |a| dhe |b| nuk janë të barabartë me 0, atëherë ab = 0 cos (a,b) = 0  (a,b) = /2, që është ajo që duhej vërtetuar.

Barazia ab = 0 merret shpesh për të përcaktuar ortogonalitetin e vektorëve.

(5.6) Përfundim. Nëse vektori a është ortogonal me secilin nga vektorët a 1 , …, A P , atëherë është ortogonal ndaj çdo kombinimi linear të tyre.

 Mjafton të theksohet se nga barazia aa 1 = ... = aa P = 0 ndjek barazinë a(x 1 A 1 + … +x P A P ) = x 1 (ahh 1 ) + … + x P (ahh P ) = 0. 

Nga përfundimi 5.6 mund të nxjerrim lehtësisht kriterin e shkollës për pingulësinë e drejtëzës dhe rrafshit. Në fakt, le të jetë një vijë MN pingul me dy drejtëza të kryqëzuara AB dhe AC. Atëherë vektori MN është ortogonal me vektorët AB dhe AC. Le të marrim çdo vijë të drejtë DE në rrafshin ABC. Vektori DE është koplanar me vektorët jokolinearë AB dhe AC, dhe për këtë arsye zgjerohet përgjatë tyre. Por atëherë ai është gjithashtu ortogonal me vektorin MN, domethënë drejtëzat MN dhe DE janë pingule. Rezulton se drejtëza MN është pingul me çdo drejtëz nga rrafshi ABC, gjë që duhej vërtetuar.

4. Bazat ortonormale. (5.7) Përkufizim. Baza e një hapësire vektoriale quhet ortonormale nëse, së pari, të gjithë vektorët e saj kanë gjatësi njësi dhe, së dyti, çdo dy nga vektorët e saj janë ortogonalë.

Vektorët e një baze ortonormale në hapësirën tredimensionale zakonisht shënohen me shkronjat i, j dhe k, dhe në rrafshin vektorial me shkronjat i dhe j. Duke marrë parasysh shenjën e ortogonalitetit të dy vektorëve dhe barazinë e katrorit skalar të një vektori me katrorin e gjatësisë së tij, kushtet për ortonormalitetin e bazës (i,j,k) të hapësirës V. 3 mund të shkruhet kështu:

(5.8) i 2 = j 2 = k 2 = 1, ij = ik = jk = 0,

dhe baza (i,j) e planit vektor - si kjo:

(5.9) i 2 = j 2 = 1, ij = 0.

Le të kenë vektorët a dhe b një bazë ortonormale (i,j,k) të hapësirës V 3 koordinatat (a 1 , A 2 , A 3 ) dhe (b 1 b 2 , b 3 ) përkatësisht. Pastajab = (A 1 i+A 2 j+A 3 k) (b 1 i+b 2 j+b 3 k) = a 1 b 1 i 2 +a 2 b 2 j 2 +a 3 b 3 k 2 +a 1 b 2 ij+a 1 b 3 ik+a 2 b 1 ji+a 2 b 3 jk+a 3 b 1 ki+a 3 b 2 kj = a 1 b 1 + a 2 b 2 + a 3 b 3 . Kështu e marrim formulën për produktin skalar të vektorëve a(a 1 ,A 2 ,A 3 ) dhe b(b 1 , b 2 , b 3 ), të dhëna nga koordinatat e tyre në bazën ortonormale të hapësirës V 3 :

(5.10) ab = a 1 b 1 + a 2 b 2 + a 3 b 3 .

Për vektorët a(a 1 ,A 2 ) dhe b(b 1 , b 2 ), e dhënë nga koordinatat e tyre në bazë ortonormale në rrafshin vektorial, ka formën

(5.11) ab = a 1 b 1 + a 2 b 2 .

Le të zëvendësojmë b = a në formulën (5.10). Rezulton se në bazë ortonormale a 2 = a 1 2 + a 2 2 + a 3 2 . Që nga një 2 = |a| 2 , marrim formulën e mëposhtme për gjetjen e gjatësisë së vektorit a(a 1 ,A 2 ,A 3 ), dhënë nga koordinatat e saj në bazën ortonormale të hapësirës V 3 :

(5.12) |a| =
.

Në rrafshin vektorial, për shkak të (5.11), merr formën

(5.13) |a| =
.

Duke zëvendësuar b = i, b = j, b = k në formulën (5.10), marrim tre barazi të tjera të dobishme:

(5.14) ai = a 1 , aj = a 2 , ak = a 3 .

Thjeshtësia e formulave të koordinatave për gjetjen e produktit skalar të vektorëve dhe gjatësisë së vektorit është përparësia kryesore e bazave ortonormale. Për bazat jo-ortonomale, këto formula janë, në përgjithësi, të pasakta dhe përdorimi i tyre në këtë rast është një gabim i madh.

5. Kosinuset e drejtimit. Le të marrim bazën ortonormale (i,j,k) të hapësirës V 3 vektori a(a 1 ,A 2 ,A 3 ). Pastajai = |a||i|kos (a,i) = |a|kos (a,i).Nga ana tjetër, ai = a 1 sipas formulës 5.14. Rezulton se

(5.15) a 1 = |a|ko (a,i).

dhe, në mënyrë të ngjashme,

A 2 = |a|ko (a,j) dhe 3 = |a|ko (a,k).

Nëse vektori a është njësi, këto tre barazi marrin një formë veçanërisht të thjeshtë:

(5.16) A 1 =cos (a,i),A 2 =cos (a,j),A 3 =cos (a,k).

Kosinuset e këndeve të formuara nga një vektor me vektorët e një baze ortonormale quhen kosinuset e drejtimit të këtij vektori në këtë bazë. Siç tregojnë formulat 5.16, koordinatat e një vektori njësi në një bazë ortonormale janë të barabarta me kosinuset e drejtimit të tij.

Nga 5.15 rrjedh se a 1 2 + a 2 2 + a 3 2 = |a| 2 (cos 2  (a,i)+cos 2  (a,j) +cos 2  (a,k)). Nga ana tjetër, a 1 2 + a 2 2 + a 3 2 = |a| 2 . Rezulton se

(5.17) shuma e katrorëve të kosinuseve të drejtimit të një vektori jozero është e barabartë me 1.

Ky fakt mund të jetë i dobishëm për zgjidhjen e disa problemeve.

(5.18) Problem. Diagonalja e një paralelipipedi drejtkëndor formon kënde 60 me dy skajet e tij që dalin nga e njëjta kulm. . Çfarë këndi formon me skajin e tretë që del nga kjo kulm?

 Konsideroni një bazë ortonormale të hapësirës V 3 , vektorët e të cilit përshkruhen nga skajet e një paralelipipedi që shtrihet nga një kulm i caktuar. Meqenëse vektori diagonal formon kënde prej 60 me dy vektorë të kësaj baze , katrorët e dy prej tre kosinuseve të drejtimit të tij janë të barabartë me cos 2 60  = 1/4. Prandaj, katrori i kosinusit të tretë është i barabartë me 1/2, dhe vetë ky kosinus është i barabartë me 1/
. Kjo do të thotë se këndi i kërkuar është 45 . 

Kështu, gjatësia e vektorit llogaritet si rrënjë katrore e shumës së katrorëve të koordinatave të tij
. Gjatësia e një vektori n-dimensionale llogaritet në mënyrë të ngjashme
. Nëse kujtojmë se çdo koordinatë e një vektori është ndryshimi midis koordinatave të fundit dhe fillimit, atëherë marrim formulën për gjatësinë e segmentit, d.m.th. Distanca Euklidiane ndërmjet pikave.

Produkt skalar dy vektorë në një rrafsh është prodhimi i gjatësisë së këtyre vektorëve dhe kosinusit të këndit ndërmjet tyre:
. Mund të vërtetohet se prodhimi skalar i dy vektorëve = (x 1, x 2) dhe = (y 1, y 2) është e barabartë me shumën e produkteve të koordinatave përkatëse të këtyre vektorëve:
= x 1 * y 1 + x 2 * y 2 .

Në hapësirën n-dimensionale, prodhimi skalar i vektorëve X= (x 1, x 2,..., x n) dhe Y= (y 1, y 2,..., y n) përcaktohet si shuma e produkteve të koordinatave të tyre përkatëse: X*Y = x 1 * y 1 + x 2 * y 2 + ... + x n * y n.

Operacioni i shumëzimit të vektorëve me njëri-tjetrin është i ngjashëm me shumëzimin e një matrice rreshti me një matricë kolone. Theksojmë se rezultati do të jetë një numër, jo një vektor.

Produkti skalar i vektorëve ka këto veti (aksioma):

1) Vetia komutative: X*Y=Y*X.

2) Vetia shpërndarëse në lidhje me mbledhjen: X(Y+Z) =X*Y+X*Z.

3) Për çdo numër real 
.

4)
, nëseX nuk është një vektor zero;
ifX është një vektor zero.

Një hapësirë ​​vektoriale lineare në të cilën është dhënë një produkt skalar i vektorëve që plotëson katër aksiomat përkatëse quhet Vektori linear Euklidianhapësirë.

Është e lehtë të shihet se kur shumëzojmë çdo vektor në vetvete, marrim katrorin e gjatësisë së tij. Pra është ndryshe gjatësia një vektor mund të përkufizohet si rrënja katrore e katrorit të tij skalar:.

Gjatësia e vektorit ka këto karakteristika:

1) |X| = 0Х = 0;

2) |X| = ||*|X|, ku është një numër real;

3) |X*Y||X|*|Y| ( Pabarazia Cauchy-Bunyakovsky);

4) |X+Y||X|+|Y| ( pabarazia e trekëndëshit).

Këndi  ndërmjet vektorëve në hapësirën n-dimensionale përcaktohet në bazë të konceptit të një produkti skalar. Në fakt, nëse
, Kjo
. Kjo thyesë nuk është më e madhe se një (sipas pabarazisë Cauchy-Bunyakovsky), kështu që nga këtu mund të gjejmë .

Të dy vektorët quhen ortogonale ose pingul, nëse produkti skalar i tyre është i barabartë me zero. Nga përkufizimi i produktit skalar rezulton se vektori zero është ortogonal me çdo vektor. Nëse të dy vektorët ortogonalë janë jo zero, atëherë cos= 0, d.m.th.=/2 = 90 o.

Le të shohim sërish figurën 7.4. Nga figura shihet se kosinusi i këndit i pjerrësisë së vektorit ndaj boshtit horizontal mund të llogaritet si
, dhe kosinusi i kënditpjerrësia e vektorit ndaj boshtit vertikal është si
. Këta numra zakonisht quhen kosinuset e drejtimit. Është e lehtë të verifikohet se shuma e katrorëve të kosinuseve të drejtimit është gjithmonë e barabartë me një: cos 2 +cos 2 = 1. Në mënyrë të ngjashme, konceptet e kosinuseve të drejtimit mund të futen për hapësirat me dimensione më të larta.

Baza e hapësirës vektoriale

Për vektorët, ne mund të përcaktojmë konceptet kombinim linear,varësia lineare Dhe pavarësinë ngjashëm me mënyrën se si u prezantuan këto koncepte për rreshtat e matricës. Është gjithashtu e vërtetë se nëse vektorët janë të varur në mënyrë lineare, atëherë të paktën njëri prej tyre mund të shprehet në mënyrë lineare në terma të të tjerëve (d.m.th., është një kombinim linear i tyre). E kundërta është gjithashtu e vërtetë: nëse njëri prej vektorëve është një kombinim linear i të tjerëve, atëherë të gjithë këta vektorë së bashku janë të varur në mënyrë lineare.

Vini re se nëse midis vektorëve a l , a 2 ,...a m ka një vektor zero, atëherë ky grup vektorësh është domosdoshmërisht i varur në mënyrë lineare. Në fakt, marrim l a l + 2 a 2 +...+ m a m = 0 nëse, për shembull, barazojmë koeficientin j në vektorin zero me një dhe të gjithë koeficientët e tjerë me zero. Në këtë rast, jo të gjithë koeficientët do të jenë të barabartë me zero ( j ≠ 0).

Përveç kësaj, nëse një pjesë e vektorëve nga një grup vektorësh janë të varur në mënyrë lineare, atëherë të gjithë këta vektorë janë të varur linearisht. Në fakt, nëse disa vektorë japin një vektor zero në kombinimin e tyre linear me koeficientë që nuk janë të dy zero, atëherë vektorët e mbetur të shumëzuar me koeficientët zero mund t'i shtohen kësaj shume produktesh, dhe do të vazhdojë të jetë një vektor zero.

Si të përcaktohet nëse vektorët janë të varur në mënyrë lineare?

Për shembull, le të marrim tre vektorë: a 1 = (1, 0, 1, 5), a 2 = (2, 1, 3, -2) dhe a 3 = (3, 1, 4, 3). Le të krijojmë një matricë prej tyre, në të cilën do të jenë kolona:

Atëherë çështja e varësisë lineare do të reduktohet në përcaktimin e rangut të kësaj matrice. Nëse rezulton të jetë e barabartë me tre, atëherë të tre kolonat janë linearisht të pavarura, dhe nëse rezulton të jetë më pak, atëherë kjo do të tregojë një varësi lineare të vektorëve.

Meqenëse renditja është 2, vektorët janë të varur në mënyrë lineare.

Vini re se zgjidhja e problemit mund të fillojë gjithashtu me arsyetimin që bazohet në përkufizimin e pavarësisë lineare. Gjegjësisht, krijoni një ekuacion vektorial  l a l + 2 a 2 + 3 a 3 = 0, i cili do të marrë formën l *(1, 0, 1, 5) + 2 *(2, 1, 3, - 2) + 3 *(3, 1, 4, 3) = (0, 0, 0, 0). Pastaj marrim një sistem ekuacionesh:

Zgjidhja e këtij sistemi duke përdorur metodën Gaussian do të reduktohet në marrjen e të njëjtës matricë hapash, vetëm se do të ketë një kolonë më shumë - terma të lirë. Të gjitha do të jenë zero, pasi transformimet lineare të zerove nuk mund të çojnë në një rezultat të ndryshëm. Sistemi i transformuar i ekuacioneve do të marrë formën:

Zgjidhja për këtë sistem do të jetë (-с;-с; с), ku c është një numër arbitrar; për shembull, (-1;-1;1). Kjo do të thotë se nëse marrim  l = -1; 2 =-1 dhe 3 = 1, atëherë l a l + 2 a 2 + 3 a 3 = 0, d.m.th. vektorët në fakt janë të varur në mënyrë lineare.

Nga shembulli i zgjidhur bëhet e qartë se nëse marrim numrin e vektorëve më të madh se dimensioni i hapësirës, ​​atëherë ata do të jenë domosdoshmërisht të varur në mënyrë lineare. Në fakt, nëse do të merrnim pesë vektorë në këtë shembull, do të merrnim një matricë 4 x 5, rangu i së cilës nuk mund të ishte më i madh se katër. ato. numri maksimal i kolonave linearisht të pavarura nuk do të ishte ende më shumë se katër. Dy, tre ose katër vektorë katërdimensionale mund të jenë linearisht të pavarur, por pesë ose më shumë jo. Rrjedhimisht, jo më shumë se dy vektorë mund të jenë linearisht të pavarur në rrafsh. Çdo tre vektor në hapësirën dydimensionale janë të varur në mënyrë lineare. Në hapësirën tre-dimensionale, çdo katër (ose më shumë) vektorë janë gjithmonë të varur në mënyrë lineare. Dhe kështu me radhë.

Kjo është arsyeja pse dimension hapësira mund të përkufizohet si numri maksimal i vektorëve linearisht të pavarur që mund të jenë në të.

Një grup prej n vektorësh të pavarur linearisht të një hapësire n-dimensionale R quhet bazë këtë hapësirë.

Teorema. Çdo vektor i hapësirës lineare mund të përfaqësohet si një kombinim linear i vektorëve bazë, dhe në një mënyrë unike.

Dëshmi. Le të formojnë vektorët e l , e 2 ,...e n një hapësirë ​​bazë-dimensionale R. Le të vërtetojmë se çdo vektor X është një kombinim linear i këtyre vektorëve. Meqenëse, së bashku me vektorin X, numri i vektorëve do të bëhet (n +1), këta (n +1) vektorë do të jenë të varur linearisht, d.m.th. ka numra l , 2 ,..., n ,, jo njëkohësisht të barabartë me zero, të tillë që

 l e l + 2 e 2 +...+ n e n +Х = 0

Në këtë rast, 0, sepse përndryshe do të merrnim l e l + 2 e 2 +...+ n e n = 0, ku jo të gjithë koeficientët l , 2 ,..., n janë të barabartë me zero. Kjo do të thotë se vektorët bazë do të vareshin në mënyrë lineare. Prandaj, ne mund t'i ndajmë të dy anët e ekuacionit të parë me:

( l /)e l + ( 2 /)e 2 +...+ ( n /)e n + X = 0

Х = -( l /)e l - ( 2 /)e 2 -...- ( n /)e n

Х = x l e l +x 2 e 2 +...+x n e n,

ku x j = -( j /),
.

Tani vërtetojmë se një paraqitje e tillë në formën e një kombinimi linear është unik. Le të supozojmë të kundërtën, d.m.th. se ka një përfaqësim tjetër:

Х = y l e l +y 2 e 2 +...+y n e n

Le të zbresim prej saj term pas termi shprehjen e marrë më parë:

0 = (y l – x 1)e l + (y 2 – x 2)e 2 +...+ (y n – x n)e n

Meqenëse vektorët bazë janë linearisht të pavarur, marrim se (y j - x j) = 0,
, pra y j = x j . Kështu që shprehja doli të ishte e njëjtë. Teorema është vërtetuar.

Shprehja X = x l e l +x 2 e 2 +...+x n e n quhet dekompozimi vektori X bazuar në e l, e 2,...e n, dhe numrat x l, x 2,...x n - koordinatat vektor x në lidhje me këtë bazë, ose në këtë bazë.

Mund të vërtetohet se nëse vektorët njozero të një hapësire Euklidiane n-dimensionale janë ortogonale në çift, atëherë ata formojnë një bazë. Në fakt, le të shumëzojmë të dyja anët e barazisë l e l + 2 e 2 +...+ n e n = 0 me çdo vektor e i. Marrim  l (e l *е i) +  2 (e 2 *е i) +...+  n (e n *е i) = 0   i (e i *е i) = 0   i = 0 për  i.

Vektorët e l , e 2 ,...e n të formës së hapësirës Euklidiane n-dimensionale bazë ortonormale, nëse këta vektorë janë dyshe ortogonalë dhe norma e secilit prej tyre është e barabartë me një, d.m.th. nëse e i *e j = 0 për i≠j и |е i | = 1 përi.

Teorema (pa prova). Në çdo hapësirë ​​Euklidiane n-dimensionale ka një bazë ortonormale.

Një shembull i një baze ortonormale është një sistem me n vektorë njësi e i, për të cilin komponenti i-të është i barabartë me një dhe komponentët e mbetur janë të barabartë me zero. Çdo vektor i tillë quhet ort. Për shembull, vektorët vektorë (1, 0, 0), (0, 1, 0) dhe (0, 0, 1) formojnë bazën e hapësirës tre-dimensionale.

Nëse në problem si gjatësitë e vektorëve ashtu edhe këndi ndërmjet tyre paraqiten "në një pjatë argjendi", atëherë gjendja e problemit dhe zgjidhja e tij duken kështu:

Shembulli 1. Janë dhënë vektorët. Gjeni produktin skalar të vektorëve nëse gjatësia e tyre dhe këndi ndërmjet tyre përfaqësohen me vlerat e mëposhtme:

Një përkufizim tjetër është gjithashtu i vlefshëm, plotësisht i barabartë me përkufizimin 1.

Përkufizimi 2. Produkti skalar i vektorëve është një numër (skalar) i barabartë me produktin e gjatësisë së njërit prej këtyre vektorëve dhe me projeksionin e një vektori tjetër në boshtin e përcaktuar nga i pari prej këtyre vektorëve. Formula sipas përkufizimit 2:

Ne do ta zgjidhim problemin duke përdorur këtë formulë pas pikës tjetër të rëndësishme teorike.

Përkufizimi i prodhimit skalar të vektorëve në terma të koordinatave

I njëjti numër mund të merret nëse vektorëve që shumëzohen u jepen koordinatat e tyre.

Përkufizimi 3. Prodhimi me pika i vektorëve është një numër i barabartë me shumën e prodhimeve në çift të koordinatave të tyre përkatëse.

Në sipërfaqe

Nëse dy vektorë dhe në rrafsh përcaktohen nga dy të tyre Koordinatat drejtkëndore karteziane

atëherë prodhimi skalar i këtyre vektorëve është i barabartë me shumën e produkteve në çift të koordinatave të tyre përkatëse:

.

Shembulli 2. Gjeni vlerën numerike të projeksionit të vektorit në boshtin paralel me vektorin.

Zgjidhje. Ne gjejmë produktin skalar të vektorëve duke shtuar prodhimet në çift të koordinatave të tyre:

Tani duhet të barazojmë produktin skalar që rezulton me produktin e gjatësisë së vektorit dhe projeksionin e vektorit në një bosht paralel me vektorin (në përputhje me formulën).

Gjeni gjatësinë e vektorit si Rrenja katrore nga shuma e katrorëve të koordinatave të saj:

.

Ne krijojmë një ekuacion dhe e zgjidhim atë:

Përgjigju. Vlera e kërkuar numerike është minus 8.

Në hapësirë

Nëse dy vektorë dhe në hapësirë ​​përcaktohen me tre koordinatat e tyre drejtkëndore karteziane

,

atëherë produkti skalar i këtyre vektorëve është gjithashtu i barabartë me shumën e produkteve në çift të koordinatave të tyre përkatëse, vetëm se tashmë ekzistojnë tre koordinata:

.

Detyra e gjetjes së produktit skalar duke përdorur metodën e konsideruar është pas analizimit të vetive të produktit skalar. Sepse në problem do t'ju duhet të përcaktoni se çfarë këndi formojnë vektorët e shumëzuar.

Vetitë e produktit skalar të vektorëve

Vetitë algjebrike

1. (veti komutative: ndryshimi i vendeve të vektorëve të shumëzuar nuk e ndryshon vlerën e prodhimit skalar të tyre).

2. (veti asociative në lidhje me një faktor numerik: prodhimi skalar i një vektori shumëzuar me një faktor të caktuar dhe një vektor tjetër është i barabartë me produktin skalar të këtyre vektorëve shumëzuar me të njëjtin faktor).

3. (veti shpërndarëse në raport me shumën e vektorëve: prodhimi skalar i shumës së dy vektorëve nga vektori i tretë është i barabartë me shumën e prodhimeve skalare të vektorit të parë nga vektori i tretë dhe i vektorit të dytë nga vektori i tretë).

4. (katrori skalar i vektorit më i madh se zero), nëse është një vektor jozero, dhe, nëse është një vektor zero.

Vetitë gjeometrike

Në përkufizimet e operacionit në studim, ne kemi prekur tashmë konceptin e një këndi midis dy vektorëve. Është koha për të sqaruar këtë koncept.

Në figurën e mësipërme mund të shihni dy vektorë që janë sjellë në një origjinë të përbashkët. Dhe gjëja e parë që duhet t'i kushtoni vëmendje është se ekzistojnë dy kënde midis këtyre vektorëve - φ 1 Dhe φ 2 . Cili nga këto kënde shfaqet në përkufizimet dhe vetitë e produktit skalar të vektorëve? Shuma e këndeve të konsideruara është 2 π dhe për këtë arsye kosinuset e këtyre këndeve janë të barabartë. Përkufizimi i produktit me pika përfshin vetëm kosinusin e këndit dhe jo vlerën e shprehjes së tij. Por vetitë marrin parasysh vetëm një kënd. Dhe ky është një nga dy këndet që nuk kalon π , pra 180 gradë. Në figurë ky kënd tregohet si φ 1 .

1. Quhen dy vektorë ortogonale Dhe këndi ndërmjet këtyre vektorëve është i drejtë (90 gradë ose π /2), nëse produkti skalar i këtyre vektorëve është zero :

.

Ortogonaliteti në algjebër vektoriale është pinguliteti i dy vektorëve.

2. Përbëhen dy vektorë jozero kënd i mprehtë (nga 0 në 90 gradë, ose, që është e njëjtë - më pak π produkti me pika është pozitiv .

3. Përbëhen dy vektorë jozero kënd i mpirë (nga 90 në 180 gradë, ose, çfarë është e njëjta - më shumë π /2) nëse dhe vetëm nëse ata produkti me pika është negativ .

Shembulli 3. Koordinatat jepen nga vektorët:

.

Llogaritni prodhimet skalare të të gjitha çifteve të vektorëve të dhënë. Çfarë këndi (akut, i drejtë, i trashë) formojnë këto çifte vektorësh?

Zgjidhje. Ne do të llogarisim duke shtuar prodhimet e koordinatave përkatëse.

Mora një numër negativ, kështu që vektorët formojnë një kënd të mpirë.

Ne morëm një numër pozitiv, kështu që vektorët formojnë një kënd të mprehtë.

Ne morëm zero, kështu që vektorët formojnë një kënd të drejtë.

Ne morëm një numër pozitiv, kështu që vektorët formojnë një kënd të mprehtë.

.

Ne morëm një numër pozitiv, kështu që vektorët formojnë një kënd të mprehtë.

Për vetë-test mund të përdorni kalkulator në internet Produkti me pika i vektorëve dhe kosinusit të këndit ndërmjet tyre .

Shembulli 4. Jepen gjatësitë e dy vektorëve dhe këndi ndërmjet tyre:

.

Përcaktoni në cilën vlerë të numrit vektorët dhe janë ortogonalë (pingulë).

Zgjidhje. Le të shumëzojmë vektorët duke përdorur rregullin për shumëzimin e polinomeve:

Tani le të llogarisim çdo term:

.

Le të krijojmë një ekuacion (produkti është i barabartë me zero), shtojmë terma të ngjashëm dhe zgjidhim ekuacionin:

Përgjigje: e morëm vlerën λ = 1.8, në të cilën vektorët janë ortogonalë.

Shembulli 5. Vërtetoni se vektori ortogonale (pingule) me vektorin

Zgjidhje. Për të kontrolluar ortogonalitetin, ne shumëzojmë vektorët dhe si polinome, duke zëvendësuar në vend të kësaj shprehjen e dhënë në deklaratën e problemit:

.

Për ta bërë këtë, duhet të shumëzoni çdo term (term) të polinomit të parë me çdo term të të dytit dhe të shtoni produktet që rezultojnë:

.

Në rezultatin që rezulton, fraksioni zvogëlohet me. Është marrë rezultati i mëposhtëm:

Përfundim: si rezultat i shumëzimit kemi marrë zero, prandaj vërtetohet ortogonaliteti (perpendikulariteti) i vektorëve.

Zgjidheni vetë problemin dhe më pas shikoni zgjidhjen

Shembulli 6. Janë dhënë gjatësitë e vektorëve dhe këndi ndërmjet këtyre vektorëve është π /4. Përcaktoni në çfarë vlere μ vektorë dhe janë reciprokisht pingul.

Për vetë-test mund të përdorni kalkulator në internet Produkti me pika i vektorëve dhe kosinusit të këndit ndërmjet tyre .

Paraqitja matricore e produktit me pika të vektorëve dhe produktit të vektorëve n-dimensionale

Ndonjëherë është e dobishme që qartësia të përfaqësojë dy vektorë të shumëzuar në formën e matricave. Pastaj vektori i parë përfaqësohet si një matricë rreshti, dhe e dyta - si një matricë kolone:

Atëherë produkti skalar i vektorëve do të jetë produkti i këtyre matricave :

Rezultati është i njëjtë me atë të marrë nga metoda që kemi shqyrtuar tashmë. Ne morëm një numër të vetëm, dhe produkti i një matrice rreshti nga një matricë kolone është gjithashtu një numër i vetëm.

Është i përshtatshëm për të paraqitur produktin e vektorëve abstraktë n-dimensionale në formë matrice. Kështu, prodhimi i dy vektorëve katërdimensionale do të jetë prodhimi i një matrice rreshti me katër elementë nga një matricë kolone gjithashtu me katër elementë, produkti i dy vektorëve pesë-dimensionale do të jetë prodhimi i një matrice rreshti me pesë elementë nga një matricë kolone gjithashtu me pesë elementë, e kështu me radhë.

Shembulli 7. Gjeni prodhimet skalare të çifteve të vektorëve

,

duke përdorur paraqitjen e matricës.

Zgjidhje. Çifti i parë i vektorëve. Ne përfaqësojmë vektorin e parë si një matricë rreshti, dhe të dytin si një matricë kolone. Ne gjejmë produktin skalar të këtyre vektorëve si produkt i një matrice rreshti dhe një matrice kolone:

Në mënyrë të ngjashme përfaqësojmë çiftin e dytë dhe gjejmë:

Siç mund ta shihni, rezultatet ishin të njëjta si për të njëjtat çifte nga shembulli 2.

Këndi ndërmjet dy vektorëve

Derivimi i formulës për kosinusin e këndit ndërmjet dy vektorëve është shumë i bukur dhe konciz.

Për të shprehur prodhimin me pika të vektorëve

(1)

në formën e koordinatave, së pari gjejmë produktin skalar të vektorëve njësi. Produkti skalar i një vektori me vetveten sipas përkufizimit:

Ajo që shkruhet në formulën e mësipërme do të thotë: produkti skalar i një vektori me vetveten është i barabartë me katrorin e gjatësisë së tij. Kosinusi i zeros është i barabartë me një, kështu që katrori i secilës njësi do të jetë i barabartë me një:

Meqenëse vektorët

janë pingul në çift, atëherë produktet në çift të vektorëve njësi do të jenë të barabarta me zero:

Tani le të kryejmë shumëzimin e polinomeve vektoriale:

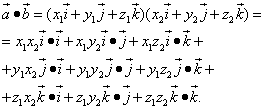
Ne zëvendësojmë vlerat e produkteve skalare përkatëse të vektorëve njësi në anën e djathtë të barazisë:

Ne marrim formulën për kosinusin e këndit midis dy vektorëve:

Shembulli 8. Janë dhënë tre pikë A(1;1;1), B(2;2;1), C(2;1;2).

Gjeni këndin.

Zgjidhje. Gjetja e koordinatave të vektorëve:

,

.

Duke përdorur formulën e këndit të kosinusit marrim:

Prandaj, .

Për vetë-test mund të përdorni kalkulator në internet Produkti me pika i vektorëve dhe kosinusit të këndit ndërmjet tyre .

Shembulli 9. Janë dhënë dy vektorë

Gjeni shumën, ndryshimin, gjatësinë, produktin e pikave dhe këndin ndërmjet tyre.

2.Diferenca

Prodhimi pikash i vektorëve

Ne vazhdojmë të merremi me vektorët. Në mësimin e parë Vektorë për dummies Ne shikuam konceptin e një vektori, veprimet me vektorë, koordinatat vektoriale dhe problemet më të thjeshta me vektorët. Nëse keni ardhur në këtë faqe për herë të parë nga një motor kërkimi, ju rekomandoj fuqimisht të lexoni artikullin hyrës të mësipërm, pasi për të zotëruar materialin duhet të njiheni me termat dhe shënimet që përdor, të keni njohuri bazë për vektorët dhe të jetë në gjendje të zgjidhë problemet themelore. Ky mësim është një vazhdim logjik i temës, dhe në të do të analizoj në detaje detyrat tipike që përdorin produktin skalar të vektorëve. Ky është një aktivitet shumë i rëndësishëm.. Mundohuni të mos i kaloni shembujt që vijnë me një bonus të dobishëm - praktika do t'ju ndihmojë të konsolidoni materialin që keni mbuluar dhe të përmirësoheni në zgjidhjen e problemeve të zakonshme në gjeometrinë analitike.

Mbledhja e vektorëve, shumëzimi i një vektori me një numër.... Do të ishte naive të mendosh se matematikanët nuk kanë dalë me diçka tjetër. Përveç veprimeve të diskutuara tashmë, ekzistojnë një sërë operacionesh të tjera me vektorë, përkatësisht: produkt pikash i vektorëve, prodhim vektorial i vektorëve Dhe produkt i përzier i vektorëve. Prodhimi skalar i vektorëve është i njohur për ne që nga shkolla, dy produktet e tjera i përkasin tradicionalisht kursit të matematikës së lartë. Temat janë të thjeshta, algoritmi për zgjidhjen e shumë problemeve është i drejtpërdrejtë dhe i kuptueshëm. E vetmja gjë. Ekziston një sasi e mirë informacioni, kështu që është e padëshirueshme të përpiqeni të zotëroni dhe zgjidhni GJITHÇKA NË NJËHERË. Kjo është veçanërisht e vërtetë për bedelet, më besoni, autori absolutisht nuk dëshiron të ndihet si Chikatilo nga matematika. Epo, jo nga matematika, natyrisht, =) Studentët më të përgatitur mund të përdorin materiale në mënyrë selektive, në një farë kuptimi, "të marrin" njohuritë që mungojnë për ju Unë do të jem një Kont Drakula i padëmshëm =)

Le të hapim më në fund derën dhe të shikojmë me entuziazëm se çfarë ndodh kur dy vektorë takohen me njëri-tjetrin...

Përkufizimi i produktit skalar të vektorëve.
Vetitë e produktit skalar. Detyra tipike

Koncepti i një produkti me pika

Së pari rreth këndi ndërmjet vektorëve. Unë mendoj se të gjithë e kuptojnë intuitivisht se cili është këndi midis vektorëve, por për çdo rast, pak më shumë detaje. Le të shqyrtojmë vektorët e lirë jozero dhe . Nëse i vizatoni këta vektorë nga një pikë arbitrare, do të merrni një pamje që shumë njerëz tashmë e kanë imagjinuar mendërisht:

E pranoj, këtu e përshkrova situatën vetëm në nivelin e të kuptuarit. Nëse keni nevojë për një përcaktim të rreptë të këndit midis vektorëve, ju lutemi referojuni tekstit shkollor për problemet praktike, në parim, ai nuk është i dobishëm për ne. Gjithashtu KETU DHE KËTU unë do të injoroj zero vektorë në vende për shkak të rëndësisë së tyre të ulët praktike. Kam bërë një rezervim posaçërisht për vizitorët e avancuar të faqes, të cilët mund të më qortojnë për paplotësinë teorike të disa deklaratave të mëvonshme.

mund të marrë vlera nga 0 në 180 gradë (0 në radian), përfshirëse. Në mënyrë analitike, ky fakt shkruhet në formën e një pabarazie të dyfishtë: ose (në radiane).

Në literaturë, simboli i këndit shpesh anashkalohet dhe shkruhet thjesht.

Përkufizimi: Prodhimi skalar i dy vektorëve është një NUMËR i barabartë me prodhimin e gjatësive të këtyre vektorëve dhe kosinusit të këndit ndërmjet tyre:

Tani ky është një përkufizim mjaft i rreptë.

Ne fokusohemi në informacionin thelbësor:

Përcaktimi: produkti skalar shënohet me ose thjesht.

Rezultati i operacionit është një NUMËR: Vektori shumëzohet me vektor, dhe rezultati është një numër. Në të vërtetë, nëse gjatësitë e vektorëve janë numra, kosinusi i një këndi është një numër, atëherë prodhimi i tyre do të jetë gjithashtu një numër.

Vetëm disa shembuj ngrohjeje:

Shembulli 1

Zgjidhja: Ne përdorim formulën . Në këtë rast:

Përgjigje:

Vlerat e kosinusit mund të gjenden në tabelë trigonometrike. Unë rekomandoj ta printoni - do të nevojitet pothuajse në të gjitha pjesët e kullës dhe do të nevojitet shumë herë.

Nga një këndvështrim thjesht matematikor, produkti skalar është pa dimension, domethënë, rezultati, në këtë rast, është vetëm një numër dhe kaq. Nga pikëpamja e problemeve të fizikës, produkti skalar ka gjithmonë një kuptim të caktuar fizik, domethënë, pas rezultatit duhet të tregoni një ose një tjetër njësi fizike. Shembull kanonik mbi llogaritjen e punës së forcës mund të gjendet në çdo tekst shkollor (formula është saktësisht një produkt skalar). Puna e një force matet në Joules, prandaj, përgjigja do të shkruhet mjaft specifike, për shembull, .

Shembulli 2

Gjeni nëse , dhe këndi ndërmjet vektorëve është i barabartë me .

Ky është një shembull për vendim i pavarur, përgjigja është në fund të mësimit.

Këndi ndërmjet vektorëve dhe vlerës së produktit me pikë

Në shembullin 1, produkti skalar doli të ishte pozitiv, dhe në shembullin 2 rezultoi negativ. Le të zbulojmë se nga varet shenja e produktit skalar. Le të shohim formulën tonë: . Gjatësitë e vektorëve jozero janë gjithmonë pozitive: , kështu që shenja mund të varet vetëm nga vlera e kosinusit.

Shënim: Për të kuptuar më mirë informacionin e mëposhtëm, është më mirë të studioni grafikun e kosinusit në manual Grafikët dhe vetitë e funksioneve. Shihni se si sillet kosinusi në segment.

Siç u përmend tashmë, këndi midis vektorëve mund të ndryshojë brenda , dhe rastet e mëposhtme janë të mundshme:

1) Nëse qoshe ndërmjet vektorëve pikante: (nga 0 në 90 gradë), atëherë , Dhe produkti me pika do të jetë pozitiv bashkëdrejtuar, atëherë këndi midis tyre konsiderohet zero, dhe produkti skalar do të jetë gjithashtu pozitiv. Meqenëse , formula thjeshton: .

2) Nëse qoshe ndërmjet vektorëve topitur: (nga 90 në 180 gradë), atëherë , dhe përkatësisht, produkti me pika është negativ: . Rast i veçantë: nëse vektorët drejtime të kundërta, atëherë merret parasysh këndi ndërmjet tyre zgjeruar: (180 gradë). Produkti skalar është gjithashtu negativ, pasi

Deklaratat e kundërta janë gjithashtu të vërteta:

1) Nëse , atëherë këndi ndërmjet këtyre vektorëve është akut. Përndryshe, vektorët janë bashkëdrejtues.

2) Nëse , atëherë këndi ndërmjet këtyre vektorëve është i mpirë. Përndryshe, vektorët janë në drejtime të kundërta.

Por rasti i tretë është me interes të veçantë:

3) Nëse qoshe ndërmjet vektorëve drejt: (90 gradë), atëherë produkti skalar është zero: . E kundërta është gjithashtu e vërtetë: nëse , atëherë . Deklarata mund të formulohet në mënyrë kompakte si më poshtë: Prodhimi skalar i dy vektorëve është zero nëse dhe vetëm nëse vektorët janë ortogonalë. I shkurtër shënimi matematik:

! shënim : Le të përsërisim bazat e logjikës matematikore: Një ikonë e pasojave logjike të dyanshme zakonisht lexohet "nëse dhe vetëm nëse", "nëse dhe vetëm nëse". Siç mund ta shihni, shigjetat drejtohen në të dy drejtimet - "nga kjo vijon kjo, dhe anasjelltas - nga kjo vijon". Nga rruga, cili është ndryshimi nga ikona e ndjekjes me një drejtim? Ikona thotë vetëm se, se “nga kjo rrjedh kjo”, dhe nuk është fakt që e kundërta është e vërtetë. Për shembull: , por jo çdo kafshë është panterë, kështu që në këtë rast nuk mund të përdorni ikonën. Në të njëjtën kohë, në vend të ikonës Mund përdorni ikonën e njëanshme. Për shembull, gjatë zgjidhjes së problemit, zbuluam se arritëm në përfundimin se vektorët janë ortogonal: - një hyrje e tillë do të jetë e saktë, dhe madje edhe më e përshtatshme se .

Rasti i tretë ka një rëndësi të madhe praktike, pasi ju lejon të kontrolloni nëse vektorët janë ortogonalë apo jo. Këtë problem do ta zgjidhim në pjesën e dytë të mësimit.

Vetitë e produktit me pika

Le të kthehemi në situatën kur dy vektorë bashkëdrejtuar. Në këtë rast, këndi ndërmjet tyre është zero, dhe formula e produktit skalar merr formën: .

Çfarë ndodh nëse një vektor shumëzohet me vetveten? Është e qartë se vektori është në linjë me vetveten, kështu që ne përdorim formulën e thjeshtuar të mësipërm:

Numri thirret katror skalar vektor, dhe shënohen si .

Kështu, katrori skalar i një vektori është i barabartë me katrorin e gjatësisë së vektorit të dhënë:

Nga kjo barazi mund të marrim një formulë për llogaritjen e gjatësisë së vektorit:

Deri më tani duket e paqartë, por objektivat e mësimit do të vendosin gjithçka në vendin e vet. Për të zgjidhur problemet na duhen gjithashtu vetitë e produktit me pika.

Për vektorët arbitrarë dhe çdo numër, vetitë e mëposhtme janë të vërteta:

1) – komutativ ose komutative ligji skalar i produktit.

2) – shpërndarja ose shpërndarës ligji skalar i produktit. Thjesht, ju mund të hapni kllapat.

3) – asociative ose asociative ligji skalar i produktit. Konstanta mund të nxirret nga produkti skalar.

Shpesh, të gjitha llojet e pronave (të cilat gjithashtu duhen provuar!) perceptohen nga studentët si mbeturina të panevojshme, të cilat vetëm duhet të mësohen përmendësh dhe të harrohen në mënyrë të sigurt menjëherë pas provimit. Duket se ajo që është e rëndësishme këtu, të gjithë e dinë që nga klasa e parë se riorganizimi i faktorëve nuk e ndryshon produktin: . Më duhet t'ju paralajmëroj se në matematikën e lartë është e lehtë të ngatërroni gjërat me një qasje të tillë. Kështu, për shembull, vetia komutative nuk është e vërtetë për matricat algjebrike. Gjithashtu nuk është e vërtetë për prodhim vektorial i vektorëve. Prandaj, së paku, është më mirë të gërmoni në çdo veçori që hasni në një kurs të lartë të matematikës, në mënyrë që të kuptoni se çfarë mund të bëni dhe çfarë nuk mund të bëni.

Shembulli 3

.

Zgjidhja: Së pari, le të sqarojmë situatën me vektorin. Çfarë është kjo gjithsesi? Shuma e vektorëve është një vektor i përcaktuar mirë, i cili shënohet me . Një interpretim gjeometrik i veprimeve me vektorë mund të gjendet në artikull Vektorë për dummies. I njëjti majdanoz me vektor është shuma e vektorëve dhe .

Pra, sipas kushtit kërkohet gjetja e produktit skalar. Në teori, ju duhet të aplikoni formulën e punës , por problemi është se nuk i dimë gjatësitë e vektorëve dhe këndin ndërmjet tyre. Por kushti jep parametra të ngjashëm për vektorët, kështu që ne do të marrim një rrugë tjetër:

(1) Zëvendësoni shprehjet e vektorëve.

(2) Ne i hapim kllapat sipas rregullit për shumëzimin e polinomeve mund të gjeni në artikull një kthesës vulgare të gjuhës Numrat kompleks ose Integrimi i një funksioni thyesor-racional. Nuk do ta përsëris veten =) Nga rruga, vetia shpërndarëse e produktit skalar na lejon të hapim kllapat. Ne kemi të drejtë.

(3) Në termat e parë dhe të fundit ne shkruajmë në mënyrë kompakte katrorët skalorë të vektorëve: . Në termin e dytë përdorim ndërrueshmërinë e produktit skalar: .

(4) Paraqesim terma të ngjashëm: .

(5) Në termin e parë përdorim formulën katrore skalar, e cila u përmend jo shumë kohë më parë. Në mandatin e fundit, në përputhje me rrethanat, e njëjta gjë funksionon: . Ne zgjerojmë termin e dytë sipas formulës standarde .

(6) Zëvendësoni këto kushte , dhe kryeni me kujdes llogaritjet përfundimtare.

Përgjigje:

Një vlerë negative e produktit skalar tregon faktin se këndi ndërmjet vektorëve është i mpirë.

Problemi është tipik, këtu është një shembull për ta zgjidhur vetë:

Shembulli 4

Gjeni produktin skalar të vektorëve dhe nëse dihet se .

Tani një detyrë tjetër e zakonshme, vetëm për formulën e re për gjatësinë e një vektori. Shënimi këtu do të jetë pak i mbivendosur, kështu që për qartësi do ta rishkruaj me një shkronjë tjetër:

Shembulli 5

Gjeni gjatësinë e vektorit nëse .

Zgjidhje do të jetë si më poshtë:

(1) Ne japim shprehjen për vektorin .

(2) Ne përdorim formulën e gjatësisë: , dhe e gjithë shprehja ve vepron si vektor "ve".

(3) Përdorimi formula e shkollës katrori i shumës. Vini re se si funksionon këtu në një mënyrë kureshtare: - në fakt, është katrori i ndryshimit dhe, në fakt, kështu është. Ata që dëshirojnë mund t'i rirregullojnë vektorët: - ndodh e njëjta gjë, deri në rirregullimin e termave.

(4) Ajo që vijon është tashmë e njohur nga dy problemet e mëparshme.

Përgjigje:

Meqenëse po flasim për gjatësinë, mos harroni të tregoni dimensionin - "njësitë".

Shembulli 6

Gjeni gjatësinë e vektorit nëse .

Ky është një shembull që ju duhet ta zgjidhni vetë. Zgjidhje e plotë dhe përgjigje në fund të mësimit.

Ne vazhdojmë të shtrydhim gjëra të dobishme nga produkti me pika. Le të shohim përsëri formulën tonë . Duke përdorur rregullin e proporcionit, ne rivendosim gjatësitë e vektorëve në emëruesin e anës së majtë:

Le të shkëmbejmë pjesët:

Cili është kuptimi i kësaj formule? Nëse dihen gjatësitë e dy vektorëve dhe produkti skalar i tyre, atëherë mund të llogaritet kosinusi i këndit midis këtyre vektorëve dhe, rrjedhimisht, vetë këndi.

A është një produkt me pika një numër? Numri. A janë gjatësitë vektoriale numra? Numrat. Kjo do të thotë se një thyesë është gjithashtu një numër. Dhe nëse dihet kosinusi i këndit: , pastaj duke përdorur funksioni i anasjelltëËshtë e lehtë të gjesh vetë këndin: .

Shembulli 7

Gjeni këndin ndërmjet vektorëve dhe nëse dihet se .

Zgjidhja: Ne përdorim formulën:

Në fazën përfundimtare të llogaritjeve, u përdor një teknikë teknike - duke eliminuar irracionalitetin në emërues. Për të eliminuar irracionalitetin, kam shumëzuar numëruesin dhe emëruesin me .

Keshtu nese , Se:

Vlerat e anasjellta funksionet trigonometrike mund të gjendet nga tabelë trigonometrike. Edhe pse kjo ndodh rrallë. Në problemet e gjeometrisë analitike, shumë më shpesh ndonjë ari i ngathët si , dhe vlera e këndit duhet të gjendet afërsisht duke përdorur një kalkulator. Në fakt, një foto të tillë do ta shohim më shumë se një herë.

Përgjigje:

Përsëri, mos harroni të tregoni dimensionet - radianët dhe shkallët. Personalisht, për të "zgjidhur qartë të gjitha pyetjet", unë preferoj të tregoj të dyja (përveç nëse kushti, natyrisht, kërkon paraqitjen e përgjigjes vetëm në radianë ose vetëm në shkallë).

Tani mund të përballeni në mënyrë të pavarur me një detyrë më komplekse:

Shembulli 7*

Janë dhënë gjatësitë e vektorëve dhe këndi ndërmjet tyre. Gjeni këndin ndërmjet vektorëve , .

Detyra nuk është aq e vështirë sa është me shumë hapa.
Le të shohim algoritmin e zgjidhjes:

1) Sipas kushtit, ju duhet të gjeni këndin midis vektorëve dhe , kështu që ju duhet të përdorni formulën .

2) Gjeni produktin skalar (shih Shembujt nr. 3, 4).

3) Gjeni gjatësinë e vektorit dhe gjatësinë e vektorit (shih Shembujt nr. 5, 6).

4) Përfundimi i zgjidhjes përkon me shembullin nr. 7 - ne e dimë numrin , që do të thotë se është e lehtë të gjesh vetë këndin:

Një zgjidhje dhe përgjigje e shkurtër në fund të mësimit.

Seksioni i dytë i mësimit i kushtohet të njëjtit produkt skalar. Koordinatat. Do të jetë edhe më e lehtë se në pjesën e parë.

Prodhimi me pika i vektorëve,
të dhëna me koordinata në bazë ortonormale

Përgjigje:

Eshtë e panevojshme të thuhet se të merresh me koordinatat është shumë më e këndshme.

Shembulli 14

Gjeni produktin skalar të vektorëve dhe nëse

Ky është një shembull që ju duhet ta zgjidhni vetë. Këtu mund të përdorni asociativitetin e operacionit, d.m.th., mos numëroni, por menjëherë merrni trefishin jashtë produktit skalar dhe shumëzojeni me të fundit. Zgjidhja dhe përgjigja janë në fund të mësimit.

Në fund të seksionit, një shembull provokues për llogaritjen e gjatësisë së një vektori:

Shembulli 15

Gjeni gjatësitë e vektorëve , Nëse

Zgjidhja: Metoda e seksionit të mëparshëm sugjeron përsëri veten: por ka një mënyrë tjetër:

Le të gjejmë vektorin:

Dhe gjatësia e saj sipas formulës së parëndësishme :

Produkti me pika nuk është fare i rëndësishëm këtu!

Gjithashtu nuk është i dobishëm kur llogaritet gjatësia e një vektori:
Ndalo. A nuk duhet të përfitojmë nga vetia e dukshme e gjatësisë së vektorit? Çfarë mund të thoni për gjatësinë e vektorit? Ky vektor 5 herë më i gjatë se vektori. Drejtimi është i kundërt, por kjo nuk ka rëndësi, sepse flasim për gjatësinë. Natyrisht, gjatësia e vektorit është e barabartë me produktin modul numrat për gjatësi vektori:
– shenja e modulit “ha” minusin e mundshëm të numrit.

Kështu:

Përgjigje:

Formula për kosinusin e këndit ndërmjet vektorëve që përcaktohen me koordinata

Tani kemi informacion të plotë për të përdorur formulën e nxjerrë më parë për kosinusin e këndit ndërmjet vektorëve shprehni përmes koordinatave vektoriale:

Kosinusi i këndit ndërmjet vektorëve të rrafshët dhe , të specifikuara në një bazë ortonormale, shprehur me formulë:
.

Kosinusi i këndit ndërmjet vektorëve hapësinorë, të specifikuara në një bazë ortonormale, shprehur me formulë:

Shembulli 16

Jepen tre kulme të një trekëndëshi. Gjeni (këndi i kulmit).

Zgjidhja: Sipas kushteve, vizatimi nuk kërkohet, por megjithatë:

Këndi i kërkuar shënohet me një hark të gjelbër. Le të kujtojmë menjëherë përcaktimin shkollor të një këndi: – vëmendje e veçantë ndaj mesatare shkronja - kjo është kulmi i këndit që na nevojitet. Për shkurtësi, ju gjithashtu mund të shkruani thjesht.

Nga vizatimi është mjaft e qartë se këndi i trekëndëshit përkon me këndin midis vektorëve dhe, me fjalë të tjera: .

Këshillohet që të mësoni se si të kryeni analizën mendërisht.

Le të gjejmë vektorët:

Le të llogarisim produktin skalar:

Dhe gjatësitë e vektorëve:

Kosinusi i këndit:

Kjo është pikërisht rendi i përfundimit të detyrës që unë rekomandoj për dummies. Lexuesit më të avancuar mund të shkruajnë llogaritjet "në një rresht":

Këtu është një shembull i një vlere "të keqe" kosinus. Vlera që rezulton nuk është përfundimtare, kështu që ka pak kuptim të heqësh qafe irracionalitetin në emërues.

Le të gjejmë vetë këndin:

Nëse shikoni vizatimin, rezultati është mjaft i besueshëm. Për të kontrolluar, këndi mund të matet edhe me një raportor. Mos e dëmtoni kapakun e monitorit =)

Përgjigje:

Në përgjigje nuk e harrojmë këtë pyeti për këndin e një trekëndëshi(dhe jo për këndin midis vektorëve), mos harroni të tregoni përgjigjen e saktë: dhe vlerën e përafërt të këndit: , gjetur duke përdorur një kalkulator.

Ata që e kanë shijuar procesin mund të llogarisin këndet dhe të verifikojnë vlefshmërinë e barazisë kanonike

Shembulli 17

Një trekëndësh përcaktohet në hapësirë ​​nga koordinatat e kulmeve të tij. Gjeni këndin midis brinjëve dhe

Ky është një shembull që ju duhet ta zgjidhni vetë. Zgjidhje e plotë dhe përgjigje në fund të mësimit

Një seksion i shkurtër përfundimtar do t'i kushtohet projeksioneve, të cilat përfshijnë gjithashtu një produkt skalar:

Projeksioni i një vektori në një vektor. Projektimi i një vektori në boshtet koordinative.
Kosinuset e drejtimit të një vektori

Merrni parasysh vektorët dhe:

Le të projektojmë vektorin në vektor për ta bërë këtë, nga fillimi dhe fundi i vektorit që ne e lëmë; pingulet te vektori (vijat e gjelbra me pika). Imagjinoni që rrezet e dritës bien pingul mbi vektor. Atëherë segmenti (vija e kuqe) do të jetë "hija" e vektorit. Në këtë rast, projeksioni i vektorit mbi vektor është GJATËSIA e segmentit. Kjo do të thotë, PROJEKCIONI ËSHTË NJË NUMËR.

Ky NUMËR shënohet si më poshtë: , “vektori i madh” tregon vektorin CILI projekti, "vektori i nënshkrimit të vogël" tregon vektorin AKTIV e cila është projektuar.

Vetë hyrja lexohet kështu: "projeksioni i vektorit "a" në vektorin "be".

Çfarë ndodh nëse vektori "be" është "shumë i shkurtër"? Ne tërheqim një vijë të drejtë që përmban vektorin "be". Dhe vektori "a" do të projektohet tashmë në drejtim të vektorit "be", thjesht - në vijën e drejtë që përmban vektorin "be". E njëjta gjë do të ndodhë nëse vektori "a" shtyhet në mbretërinë e tridhjetë - ai ende do të projektohet lehtësisht në vijën e drejtë që përmban vektorin "be".

Nëse këndi ndërmjet vektorëve pikante(si në foto), atëherë

Nëse vektorët ortogonale, atëherë (projeksioni është një pikë dimensionet e së cilës konsiderohen zero).

Nëse këndi ndërmjet vektorëve topitur(në figurë, rirregulloni mendërisht shigjetën vektoriale), më pas (e njëjta gjatësi, por e marrë me shenjën minus).

Le t'i vizatojmë këta vektorë nga një pikë:

Natyrisht, kur një vektor lëviz, projeksioni i tij nuk ndryshon