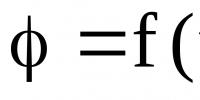Tipične dinamičke veze sistema automatskog upravljanja. Tipične ACS jedinice Elementarne dinamičke jedinice
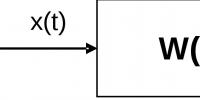
Šta je dinamička veza? U prethodnim lekcijama razmatrali smo pojedine dijelove sistema automatskog upravljanja i nazivali ih elementi sistemi automatskog upravljanja. Elementi mogu imati različit fizički izgled i dizajn. Glavna stvar je da neki unos x( t ) , a kao odgovor na ovaj ulazni signal, element upravljačkog sistema formira neke izlazni signal y( t ) . Zatim smo otkrili da je odnos između izlaznog i ulaznog signala određen dinamička svojstva kontrola, koja se može predstaviti kao prijenosna funkcija W(s). Dakle, evo ga dinamička veza je svaki element sistema automatskog upravljanja koji ima određeni matematički opis, tj. za koje je poznata prijenosna funkcija.

Rice. 3.4. Element (a) i dinamička veza (b) ACS.
Tipične dinamičke veze je minimalni potreban skup veza za opisivanje proizvoljnog tipa kontrolnog sistema. Tipične veze uključuju:
proporcionalna veza;
aperiodična veza 1. reda;
aperiodična veza drugog reda;
oscilatorna veza;
integrirajuća veza;
idealna diferencirajuća karika;
forsirajuća karika 1. reda;
forsirajuća karika drugog reda;
veza sa čistim kašnjenjem.
proporcionalna veza
Proporcionalna veza se također naziva bez inercije .
1. Transfer funkcija.
Prijenosna funkcija proporcionalne veze ima oblik:
W(s) = K gdje je K faktor pojačanja.
Proporcionalna veza je opisana algebarskom jednadžbom:
y(t) = K· X(t)
Primjeri takvih proporcionalnih karika su polužni mehanizam, kruti mehanički prijenos, mjenjač, elektronski pojačivač signala na niskim frekvencijama, razdjelnik napona itd.



4. Prijelazna funkcija .
Prijelazna funkcija proporcionalne karike ima oblik:
h(t) = L -1 = L -1 = K· 1(t)
5. Funkcija težine.
Funkcija težine proporcionalne karike je:
w(t) = L -1 = Kδ(t)




Rice. 3.5. Prijelazna funkcija, funkcija težine, fazni odziv i proporcionalni odziv .
6. Frekventne karakteristike .
Nađimo AFC, AFC, PFC i LAH proporcionalne veze:
W(jω ) = K = K +0j
A(ω
)
=
 = K
= K
φ(ω) = arctg(0/K) = 0
L(ω) = 20 log = 20 log(K)
Kao što slijedi iz prikazanih rezultata, amplituda izlaznog signala ne ovisi o frekvenciji. U stvarnosti, nijedna veza ne može jednoliko da prođe sve frekvencije od 0 do ¥, po pravilu, na visokim frekvencijama, pojačanje postaje manje i teži nuli pri ω → ∞. Na ovaj način, matematički model proporcionalne veze je neka idealizacija stvarnih veza .
Aperiodična veza I th order
Aperiodične veze se također nazivaju inercijalni .
1. Transfer funkcija.
Prijenosna funkcija aperiodične veze 1. reda ima oblik:
W(s) = K/(T· s + 1)
gdje je K faktor pojačanja; T je vremenska konstanta koja karakteriše inerciju sistema, tj. trajanje procesa tranzicije u njemu. Zbog vremenska konstanta karakteriše neki vremenski interval , tada njegova vrijednost mora uvijek biti pozitivna, tj. (T > 0).
2. Matematički opis veze.
Aperiodična veza 1. reda opisuje se diferencijalnom jednačinom prvog reda:
T· dy(t)/ dt+ y(t) = K·X(t)
3. Fizička implementacija veze.
Primjeri aperiodične veze 1. reda su: električni RC filter; termoelektrični pretvarač; rezervoar za komprimovani gas itd.



4. Prijelazna funkcija .
Prijelazna funkcija aperiodične veze 1. reda ima oblik:
h(t) = L -1 = L -1 = K – K e -t/T = K (1 – e -t/T )


Rice. 3.6. Prolazni odziv aperiodične veze 1. reda.
Prolazni proces aperiodične veze prvog reda ima eksponencijalni oblik. Stabilna vrijednost je: h set = K. Tangenta u tački t = 0 prelazi liniju stabilne vrijednosti u tački t = T. U trenutku t = T, funkcija prijelaza uzima vrijednost: h(T) ≈ 0,632 K, tokom vremena T, prelazni odziv dobija samo oko 63% vrednosti stabilnog stanja.
Hajde da definišemo vreme regulisanja T at za aperiodičnu vezu 1. reda. Kao što je poznato iz prethodnog predavanja, regulaciono vrijeme je vrijeme nakon kojeg razlika između trenutnih i stabilnih vrijednosti neće preći neku zadatu malu vrijednost Δ. (Uobičajeno, ∆ se daje kao 5% stabilnog stanja).
h(T y) \u003d (1 - Δ) h set = (1 - Δ) K = K (1 - e - T y / T), dakle e - T y / T = Δ, zatim T y / T \u003d -ln (Δ), kao rezultat, dobijamo T y \u003d [-ln (Δ)] T.
Kod Δ = 0,05 T y = - ln(0,05) T ≈ 3 T.
Drugim riječima, vrijeme prolaznog procesa aperiodične veze prvog reda je približno 3 puta veće od vremenske konstante.
Tipične dinamičke veze i njihove karakteristike
dinamička veza naziva se element sistema koji ima određena dinamička svojstva.
Svaki sistem se može predstaviti kao ograničen skup tipičnih elementarnih veza, koje mogu biti bilo koje prirode, dizajna i svrhe. Prijenosna funkcija bilo kojeg sistema može se predstaviti kao frakciona racionalna funkcija:
(1)Dakle, prijenosna funkcija bilo kojeg sistema može se predstaviti kao proizvod prostih faktora i prostih razlomaka. Veze, čije su prijenosne funkcije u obliku jednostavnih faktora ili prostih razlomaka, nazivaju se tipičnim ili elementarnim vezama. Tipične veze se razlikuju po obliku svoje funkcije prijenosa, što određuje njihova statička i dinamička svojstva.
Kao što se može vidjeti iz dekompozicije, mogu se razlikovati sljedeće veze:
1. Pojačavanje (bez inercije).
2. Diferenciranje.
3. Prisilna veza 1. reda.
4. Prisilna veza 2. reda.
5. Integracija.
6. Aperiodični (inercijalni).
7. Vibracioni.
8. Odgođeno.
Kada se proučavaju sistemi automatskog upravljanja, on se predstavlja kao skup elemenata ne prema njihovoj funkcionalnoj namjeni ili fizičkoj prirodi, već prema njihovim dinamičkim svojstvima. Za izgradnju upravljačkih sistema potrebno je poznavati karakteristike tipičnih veza. Glavne karakteristike veza su diferencijalna jednadžba i prijenosna funkcija.
Razmotrite glavne veze i njihove karakteristike.
Pojačavajuća veza(bez inercije, proporcionalno). Poziva se pojačavajuća veza, koja je opisana jednadžbom:
ili prijenosna funkcija:
(3)U ovom slučaju, prelazna funkcija pojačalačke veze (slika 1a) i njena težinska funkcija (slika 1b), respektivno, imaju oblik:
Frekventne karakteristike veze (slika 2) mogu se dobiti iz njene funkcije prijenosa, dok su AFC, AFC i PFC određeni sljedećim odnosima:
.
Logaritamski frekventni odziv pojačalačke veze (slika 3) određen je relacijom
.Primjeri veza:
1. Pojačala, na primjer, jednosmjerne struje (slika 4a).
2. Potenciometar (slika 4b).
3. Reduktor (slika 5).
Logaritamske frekvencijske karakteristike veze (slika 8) određene su formulom
To su asimptotske logaritamske karakteristike, prava karakteristika se poklapa s njom u području visokih i niskih frekvencija, a maksimalna greška će biti u tački koja odgovara pridruženoj frekvenciji, i iznosi oko 3 dB. U praksi se obično koriste asimptotske karakteristike. Njihova glavna prednost je u tome što prilikom promjene parametara sistema ( k i T) karakteristike se kreću paralelno sa sobom.
Primjeri veza:
1. Aperiodična veza može biti implementirana na operacionim pojačavačima (slika 9).
ÆÆ
OTP BISN (KSN)
Svrha rada– sticanje od strane studenata praktičnih vještina u korišćenju metoda za projektovanje integrisanih (složenih) sistema nadzora na brodu.
Laboratorijski rad se izvodi u računarskoj nastavi.
Programsko okruženje: MATLAB.
Integrisani (kompleksni) sistemi za nadzor u vazduhu su dizajnirani da rešavaju probleme traženja, detekcije, prepoznavanja, određivanja koordinata objekata pretrage itd.
Jedan od glavnih pravaca za povećanje efikasnosti rješavanja postavljenih ciljeva je racionalno upravljanje resursima pretraživanja.
Konkretno, ako su nosači IOS-a bespilotne letjelice (UAV), tada se upravljanje resursima pretraživanja sastoji u planiranju putanja i kontroli leta UAV-a, kao i kontroli linije vidljivosti IOS-a itd.
Rješenje ovih problema zasniva se na teoriji automatskog upravljanja.
Laboratorija 1
Tipične veze automatskog upravljačkog sistema (ACS)
Funkcija prijenosa
U teoriji automatskog upravljanja (TAU) često se koristi operatorski oblik pisanja diferencijalnih jednačina. U ovom slučaju se uvodi koncept diferencijalnog operatora p = d/dt tako, dy/dt = py , a p n = d n /dt n . Ovo je samo još jedna notacija za operaciju diferencijacije.
Operacija integracije inverzna diferencijaciji se zapisuje kao 1/p . U obliku operatora, originalna diferencijalna jednadžba je napisana kao algebarska:
a o p (n) y + a 1 p (n-1) y + ... + a n y = (a o p (n) + a 1 p (n-1) + ... + a n)y = (b o p (m) + b 1 p (m-1) + ... + bm)u
Ovaj oblik notacije ne treba brkati s operativnim računom, makar samo zato što se vremenske funkcije ovdje direktno koriste y(t), u(t) (originali), ne njihov Slike Y(p), U(p) , dobivenih iz originala korištenjem formule Laplaceove transformacije. Istovremeno, pod nultim početnim uslovima, do notacije, unosi su zaista veoma slični. Ova sličnost leži u prirodi diferencijalnih jednadžbi. Stoga su neka pravila operativnog računa primjenjiva na operatorski oblik jednadžbe dinamike. Dakle operater str može se smatrati faktorom bez prava na permutaciju, tj py yp. Može se izvaditi iz zagrada itd.
Stoga se jednadžba dinamike može napisati i u obliku:
Diferencijalni operator W(p) pozvao prijenosna funkcija. Određuje omjer izlazne vrijednosti veze i ulaza u svakom trenutku: W(p) = y(t)/u(t) , zato se i zove dinamički dobitak.
u stabilnom stanju d/dt = 0, to je p = 0, pa se funkcija prijenosa pretvara u koeficijent prijenosa veze K = b m / a n .
Nazivnik prijenosne funkcije D(p) = a o p n + a 1 p n - 1 + a 2 p n - 2 + ... + a n pozvao karakteristični polinom. Njegovi korijeni, tj. vrijednosti p za koje je nazivnik D(p) ide na nulu i W(p) teži beskonačnosti se zove stupovi prijenosne funkcije.
Brojač K(p) = b o p m + b 1 p m - 1 + ... + b m pozvao dobit operatera. Njegovi korijeni, koji K(p) = 0 i W(p) = 0, pozvao nule prijenosne funkcije.
Poziva se ACS veza s poznatom funkcijom prijenosa dinamička veza. Predstavljen je pravougaonikom, unutar kojeg je upisan izraz funkcije prijenosa. To jest, ovo je obična funkcionalna veza, čija je funkcija data matematičkom ovisnošću izlazne vrijednosti o ulaznoj vrijednosti u dinamičkom modu. Za vezu s dva ulaza i jednim izlazom, za svaki od ulaza moraju biti zapisane dvije funkcije prijenosa. Prijenosna funkcija je glavna karakteristika veze u dinamičkom načinu rada, iz koje se mogu dobiti sve ostale karakteristike. Određuje se samo sistemskim parametrima i ne ovisi o ulaznim i izlaznim vrijednostima. Na primjer, jedna od dinamičkih veza je integrator. Njegova prijenosna funkcija W i (p) = 1/p. ACS šema, sastavljena od dinamičkih veza, se zove strukturalni.
Veza za razlikovanje
Postoje idealne i stvarne veze koje razlikuju. Dinamička jednačina idealne veze:
y(t) = k(du/dt), ili y=kpu .
Ovdje je izlazna količina proporcionalna brzini promjene ulazne količine. Funkcija prijenosa: W(p) = kp . At k = 1 veza vrši čistu diferencijaciju W(p) = p . Privremeni odgovor: h(t) = k 1’(t) = d(t) .
Idealna diferencirajuća veza se ne može realizovati, budući da je veličina skoka izlazne vrijednosti kada se jednokratna akcija primjenjuje na ulaz uvijek ograničena. U praksi se koriste stvarne diferencirajuće veze koje izvode aproksimativno diferenciranje ulaznog signala.
Njegova jednadžba: Tpy + y = kTpu .
Funkcija prijenosa: W(p) = k(Tp/Tp + 1).
Kada se akcija u jednom koraku primeni na ulaz, izlazna vrednost je ograničena po veličini i rastegnuta u vremenu (slika 5).

Prema prolaznom odzivu, koji ima oblik eksponencijala, moguće je odrediti koeficijent prijenosa k i vremenska konstanta T. Primjeri takvih veza mogu biti mreža s četiri terminala otpora i kapacitivnosti ili otpora i induktivnosti, prigušivač, itd. Diferencijalne veze su glavni alat koji se koristi za poboljšanje dinamičkih svojstava ACS-a.
Pored razmatranih, postoji niz veza na kojima se nećemo detaljno zadržavati. To uključuje idealnu forsirajuću vezu ( W(p) = Tp + 1 , praktično neostvarivo), prava forsirajuća karika (W(p) = (T 1 p + 1)/(T 2 p + 1) , at T1 >> T2 ), retardirani link ( W(p) = e - pT ), reprodukcija ulazne akcije s vremenskim kašnjenjem i drugo.
Veza bez inercije
Funkcija prijenosa:
AFC: W(j) = k.
Realni frekventni odziv (VCH): P() = k.
Imaginarni frekvencijski odziv (MFH): Q() = 0.
Amplitudno-frekvencijska karakteristika (AFC): A() = k.
Fazni frekvencijski odziv (PFC): () = 0.
Logaritamski frekventni odziv (LAFC): L() = 20lgk.
Neki frekventni odgovori su prikazani na Sl.7.

Veza prolazi sve frekvencije podjednako sa povećanjem amplitude za k puta i bez faznog pomaka.
Integrirajuća veza
Funkcija prijenosa:
Razmotrimo poseban slučaj kada je k = 1, tj.
AFC: W(j) =  .
.
VCH: P() = 0.
MCH: Q() = - 1/ .
Frekvencijski odziv: A() = 1/ .
PFC: () = - /2.
LAF: L() = 20lg(1/ ) = - 20lg().
Frekvencijski odziv je prikazan na slici 8.

Veza propušta sve frekvencije sa faznim kašnjenjem od 90 stepeni. Amplituda izlaznog signala raste sa smanjenjem frekvencije, a smanjuje se na nulu sa povećanjem frekvencije (link "puni" visoke frekvencije). LAFC je prava linija koja prolazi kroz tačku L() = 0 na = 1. Sa povećanjem frekvencije po dekadi, ordinata se smanjuje za 20lg10 = 20 dB, odnosno nagib LAFC-a je - 20 dB/dec ( decibela po deceniji).
Aperiodična veza
Za k = 1 dobijamo sljedeće FH izraze:
W(p) = 1/(Tp + 1);
 ;
;
 ;
;
 ;
;
() = 1 - 2 = - arctg( T);
 ;
;
L() = 20lg(A()) = - 10lg(1 + (T)2).
Ovdje su A1 i A2 amplitude brojnika i nazivnika LPFC-a; 1 i 2 su argumenti brojnika i nazivnika. LPCH:
Frekvencijski odziv je prikazan na Sl.9.

AFC je polukrug poluprečnika 1/2 sa centrom u tački P = 1/2. Kada se konstruiše asimptotski LAFC, smatra se da kada< 1 = 1/T можно пренебречь ( T) 2 выражении для L(), то есть L() - 10lg1 = 0.. При >1 zanemarimo jedinicu u izrazu u zagradama, odnosno L(ω) - 20lg(ω T). Stoga LAFC prolazi duž apscise do frekvencije ugla, a zatim - pod kutom - 20 dB / dec. Frekvencija ω 1 naziva se ugaona frekvencija. Maksimalna razlika između realnog LAFC i asimptotičkog ne prelazi 3 dB pri = 1.
LPCH asimptotski teži nuli kako ω opada na nulu (što je niža frekvencija, to je manje fazno izobličenje signala) i do - /2 kako se povećava do beskonačnosti. Prevojna tačka = 1 na () = - /4. LPFC svih aperiodičnih veza imaju isti oblik i može se konstruirati iz tipične krive s paralelnim pomakom duž ose frekvencije.
Obrazac za prijavu
Elektronski izvještaj mora sadržavati:
1. Grupa, puno ime student
2. Naziv laboratorijskog rada, tema, opcija zadatka;
3. Šeme tipičnih veza;
4. Rezultati proračuna: tranzijenti, LAFC, za različite parametre linkova, grafike;
5. Zaključci na osnovu rezultata proračuna.
Laboratorijski rad 2.
Princip kompenzacije
Ako uznemirujući faktor izobliči izlaznu vrijednost do neprihvatljivih granica, primijenite princip kompenzacije(Sl. 6, KU - korektivni uređaj).
Neka y about- vrijednost izlazne količine koju je potrebno obezbijediti prema programu. U stvari, zbog perturbacije f, izlaz registruje vrijednost y. Vrijednost e \u003d y o - y pozvao odstupanje od zadate vrednosti. Ako je nekako moguće izmjeriti vrijednost f, tada se kontrolna akcija može ispraviti u na ulazu op-pojačala, sumiranjem CU signala s korektivnom akcijom proporcionalnom smetnji f i nadoknadi njegov efekat.
Primeri kompenzacionih sistema: bimetalno klatno u satu, kompenzacioni namotaj DC mašine itd. Na slici 4, postoji toplotni otpor u krugu grejnog elementa (NE). R t , čija vrijednost varira u zavisnosti od fluktuacija temperature okoline, ispravljajući napon na NO.

Vrlina principa kompenzacije: brza reakcija na smetnje. To je preciznije od principa otvorene petlje. Mana: nemogućnost uzimanja u obzir svih mogućih perturbacija na ovaj način.
Princip povratne sprege
Najviše se koristi u tehnologiji princip povratne sprege(Sl.5).

Ovdje se kontrolna varijabla korigira ovisno o izlaznoj vrijednosti y(t). I nije važno kakve perturbacije djeluju na OS. Ako vrijednost y(t) odstupa od potrebnog, tada se signal koriguje u(t) da se ovo odstupanje smanji. Veza između izlaza op-pojačala i njegovog ulaza se zove glavna povratna informacija (OS).
U posebnom slučaju (slika 6), memorija generiše traženu vrijednost izlazne vrijednosti y o (t), koji se upoređuje sa stvarnom vrijednošću na izlazu ACS-a y(t).

Devijacija e = y o -y sa izlaza uređaja za upoređivanje se dovodi na ulaz regulator R, koji kombinuje UU, UO, CHE.
Ako a e 0, tada kontroler generiše kontrolnu akciju u(t), djelujući dok se ne osigura ravnopravnost e = 0, ili y = y o. Budući da se razlika signala primjenjuje na regulator, takva povratna sprega se naziva negativan, Za razliku od pozitivne povratne informacije kada se dodaju signali.
Takva kontrola u funkciji odstupanja naziva se regulacija, a takav ACS se zove automatski sistem upravljanja(SAR).
Nedostatak inverznog principa veza je inercija sistema. Stoga se često koristi kombinacija ovog principa sa principom kompenzacije, što vam omogućava da kombinujete prednosti oba principa: brzinu reagovanja na poremećaj principa kompenzacije i tačnost regulacije, bez obzira na prirodu poremećaja principa povratne sprege.
Glavne vrste ACS-a
Ovisno o principu i zakonu funkcioniranja memorije koja postavlja program za promjenu izlazne vrijednosti, razlikuju se glavne vrste ACS-a: stabilizacijski sistemi, softver, praćenje i samopodešavanje sistema, među kojima su ekstremno, optimalno i adaptivni sistemi.
AT stabilizacijski sistemi osigurava se konstantna vrijednost kontrolirane varijable za sve vrste smetnji, tj. y(t) = konst. Memorija generiše referentni signal s kojim se upoređuje izlazna vrijednost. Memorija, po pravilu, omogućava postavljanje referentnog signala, koji vam omogućava da promijenite vrijednost izlazne količine po želji.
AT softverski sistemi promjena kontrolirane vrijednosti je osigurana u skladu s programom koji generiše memorija. Kao memorija se može koristiti mehanizam za brušenje, bušena traka ili čitač magnetne trake itd. Ovoj vrsti samohodnih pušaka mogu se pripisati igračke sa satom, kasetofoni, plejeri itd. Razlikovati sistemi sa vremenskim programom pružanje y = f(t), i sistemi sa prostornim programom, u kojem y = f(x), koji se koristi tamo gde je važno dobiti potrebnu putanju u prostoru na izlazu ACS-a, na primer, u kopirnoj mašini (slika 7), zakon kretanja u vremenu ovde ne igra ulogu.

sistemi za praćenje razlikuju se od softverskih programa samo po tome što program y = f(t) ili y = f(x) nepoznato unapred. Uređaj koji prati promjenu nekog vanjskog parametra djeluje kao memorija. Ove promjene će odrediti promjene u izlaznoj vrijednosti ACS-a. Na primjer, ruka robota koja oponaša pokrete ljudske ruke.
Sva tri razmatrana tipa ACS-a mogu se izgraditi u skladu sa bilo kojim od tri osnovna principa upravljanja. Odlikuju se zahtjevom da se izlazna vrijednost poklapa sa nekom propisanom vrijednošću na ulazu ACS-a, koja se sama može mijenjati. To jest, u svakom trenutku, tražena vrijednost izlazne količine je jednoznačno određena.
AT sistemi za samopodešavanje Memorija traži takvu vrijednost kontrolirane varijable, koja je u nekom smislu optimalna.
Dakle unutra ekstremni sistemi(Sl. 8) potrebno je da izlazna vrijednost uvijek uzima ekstremnu vrijednost od svih mogućih, koja nije unaprijed određena i može se nepredvidivo promijeniti.

Da bi ga pronašao, sistem izvodi male probne pomake i analizira odgovor izlazne vrijednosti na ove pokušaje. Nakon toga, generira se kontrolna akcija koja dovodi izlaznu vrijednost bliže ekstremnoj vrijednosti. Proces se neprekidno ponavlja. Pošto ACS podaci kontinuirano vrednuju izlazni parametar, oni se izvode samo u skladu sa trećim principom upravljanja: principom povratne sprege.
Optimalni sistemi su složenija verzija ekstremnih sistema. Ovdje se u pravilu javlja složena obrada informacija o prirodi promjene izlaznih vrijednosti i smetnji, o prirodi utjecaja upravljačkih radnji na izlazne vrijednosti, teorijske informacije, informacije heurističke prirode itd. može biti uključen. Stoga je glavna razlika između ekstremnih sistema prisustvo kompjutera. Ovi sistemi mogu raditi u skladu sa bilo kojim od tri osnovna principa kontrole.
AT adaptivni sistemi obezbeđena je mogućnost automatske rekonfiguracije parametara ili promene u šemi ACS-a radi prilagođavanja promenljivim spoljašnjim uslovima. Shodno tome, postoje samopodešavanje i samoorganizirajući se adaptivni sistemi.
Svi tipovi ACS-a osiguravaju da izlazna vrijednost odgovara traženoj vrijednosti. Jedina razlika je u programu za promjenu tražene vrijednosti. Stoga su temelji TAU-a izgrađeni na analizi najjednostavnijih sistema: stabilizacijskih sistema. Pošto smo naučili da analiziramo dinamička svojstva ACS-a, uzet ćemo u obzir sve karakteristike složenijih tipova ACS-a.
Statičke karakteristike
Poziva se način rada ACS-a, u kojem se kontrolirana varijabla i sve međuvrijednosti ne mijenjaju u vremenu uspostavljena, ili statički način rada. Opisani su svi linkovi i ACS kao cjelina u ovom načinu rada jednačine statike vrsta y = F(u,f) u kojoj nema vremena t. Pozivaju se odgovarajući grafovi statičke karakteristike. Statička karakteristika veze sa jednim ulazom u može se predstaviti krivom y = F(u)(Sl. 9). Ako veza ima drugi ulaz perturbacije f, tada je statička karakteristika data familijom krivulja y = F(u) na različitim vrijednostima f, ili y = F(f) na raznim u.



Dakle, primjer jedne od funkcionalnih karika kontrolnog sistema je konvencionalna poluga (slika 10). Jednačina statike za to ima oblik y = Ku. Može se predstaviti kao veza čija je funkcija da pojača (ili priguši) ulazni signal K jednom. Koeficijent K = y/u, jednak omjeru izlazne vrijednosti i ulazne se poziva dobitak veza. Kada su ulazne i izlazne veličine različite prirode, to se zove prenosni odnos.
Statička karakteristika ove veze ima oblik pravolinijskog segmenta sa nagibom a = arctg(L 2 /L 1) = arctg(K)(Sl. 11). Veze sa linearnim statičkim karakteristikama se nazivaju linearno. Statičke karakteristike stvarnih veza su, po pravilu, nelinearne. Takve veze se nazivaju nelinearne. Karakterizira ih ovisnost koeficijenta prijenosa od veličine ulaznog signala: K = y/ u konst.
Na primjer, statička karakteristika zasićenog DC generatora prikazana je na slici 12. Obično se nelinearna karakteristika ne može izraziti nikakvom matematičkom zavisnošću i mora se specificirati u tabeli ili grafikonu.



Poznavajući statičke karakteristike pojedinih veza, moguće je konstruisati statičku karakteristiku ACS-a (sl. 13, 14). Ako su sve veze ACS-a linearne, tada ACS ima linearnu statičku karakteristiku i poziva se linearno. Ako je barem jedna veza nelinearna, onda je ACS nelinearni.
Veze za koje možete postaviti statičku karakteristiku u obliku krute funkcionalne zavisnosti izlazne vrijednosti od ulaza nazivaju se statički. Ako ne postoji takva veza i svaka vrijednost ulazne veličine odgovara skupu vrijednosti izlazne veličine, tada se takva veza naziva astatic. Opisivanje njegovih statičkih karakteristika je besmisleno. Primjer astatičke veze je motor čija je ulazna vrijednost
voltaža U, a izlaz - ugao rotacije osovine, čija je vrijednost na U = konst može poprimiti bilo koju vrijednost.
Izlazna vrijednost astatičke veze, čak iu stabilnom stanju, je funkcija vremena.
Laboratorija 3
Dinamički način rada ACS-a
Jednačina dinamike
Stabilno stanje nije tipično za ACS. Obično na kontrolirani proces utječu različite perturbacije koje odstupaju kontrolirani parametar od zadane vrijednosti. Poziva se proces uspostavljanja željene vrijednosti kontrolirane varijable regulacija. Zbog inercije karika, regulacija se ne može izvršiti trenutno.
Razmotrimo automatski sistem upravljanja, koji je u stabilnom stanju, karakteriziran vrijednošću izlazne veličine y=yo. Neka trenutno t = 0 bilo koji uznemirujući faktor je delovao na objekat, odstupajući od vrednosti kontrolisane varijable. Nakon nekog vremena, regulator će vratiti ACS u prvobitno stanje (uzimajući u obzir statičku tačnost) (slika 1).

Ako se regulirana vrijednost mijenja u vremenu prema aperiodičnom zakonu, tada se naziva proces regulacije aperiodično.

Uz oštre smetnje moguće je oscilatorno prigušeno proces (slika 2a). Postoji i takva mogućnost da nakon nekog vremena T str u sistemu će se uspostaviti neprigušene oscilacije regulisane vrednosti - neprigušeni oscilatorni proces (slika 2b). Poslednji pogled - divergentno oscilatorno proces (slika 2c).
Dakle, razmatra se glavni način rada ACS-a dinamički način rada, karakteriziran protokom u njemu tranzijenti. Zbog toga drugi glavni zadatak u razvoju ACS-a je analiza dinamičkih načina rada ACS-a.
Opisano je ponašanje ACS-a ili bilo koje njegove veze u dinamičkim modovima jednačina dinamike y(t) = F(u,f,t), koji opisuje promjenu vrijednosti tokom vremena. Po pravilu, ovo je diferencijalna jednačina ili sistem diferencijalnih jednačina. Zbog toga glavna metoda za proučavanje ACS-a u dinamičkim režimima je metoda rješavanja diferencijalnih jednačina. Redoslijed diferencijalnih jednadžbi može biti prilično visok, odnosno, i ulazna i izlazna veličina zavise od ovisnosti u(t), f(t), y(t), te stope njihove promjene, ubrzanja itd. Stoga se jednadžba dinamike u opštem obliku može napisati na sljedeći način:
F(y, y', y”,..., y (n) , u, u', u”,..., u (m) , f, f ', f “..., f ( k)) = 0.
Na linearizirani ACS, možete primijeniti princip superpozicije: reakcija sistema na nekoliko istovremeno delujućih ulaznih akcija jednaka je zbiru reakcija na svaku akciju posebno. Ovo omogućava vezu sa dva ulaza u i f razložiti na dvije veze, od kojih svaka ima jedan ulaz i jedan izlaz (slika 3).

Stoga ćemo se u budućnosti ograničiti na proučavanje ponašanja sistema i veza sa jednim ulazom, čija jednačina dinamike ima oblik:
a o y (n) + a 1 y (n-1) + ... + a n - 1 y' + a n y = b o u (m) + ... + b m - 1u' + b m u.
Ova jednadžba opisuje ACS u dinamičkom režimu samo približno sa tačnošću datom linearizacijom. Međutim, treba imati na umu da je linearizacija moguća samo uz dovoljno mala odstupanja vrijednosti i u nedostatku diskontinuiteta u funkciji F u blizini nas interesantne tačke koju mogu kreirati razni prekidači, releji itd.
Obično nm, jer at n< m ACS je tehnički neizvodljiv.
Strukturni dijagrami ACS-a
Ekvivalentne transformacije blok dijagrama
Blok dijagram ACS-a u najjednostavnijem slučaju izgrađen je od elementarnih dinamičkih veza. Ali nekoliko elementarnih veza može se zamijeniti jednom vezom sa složenom funkcijom prijenosa. Za to postoje pravila za ekvivalentnu transformaciju blok dijagrama. Razmotrimo moguće načine transformacije.
1. serijska veza(Sl. 4) - izlazna vrijednost prethodne veze se dovodi na ulaz sljedeće. U ovom slučaju možete napisati:
y 1 = W 1 y o ; y 2 \u003d W 2 y 1; ...; y n = W n y n - 1 =>
y n \u003d W 1 W 2 ..... W n .y o \u003d W eq y o,
gdje  .
.
To jest, lanac serijski povezanih karika pretvara se u ekvivalentnu kariku s prijenosnom funkcijom jednakom proizvodu prijenosnih funkcija pojedinih karika.
2. Paralelno - suglasnički spoj(Sl. 5) - isti signal se primjenjuje na ulaz svake veze, a izlazni signali se dodaju. onda:
y \u003d y 1 + y 2 + ... + y n \u003d (W 1 + W 2 + ... + W3) y o = W eq y o,
gdje  .
.

Odnosno, lanac veza povezanih paralelno - prema, pretvara se u vezu s prijenosnom funkcijom jednakom zbiru prijenosnih funkcija pojedinih karika.
3. Paralelno - brojač priključak(Sl. 6a) - veza je pokrivena pozitivnim ili negativnim povratnim informacijama. Dio kola duž kojeg signal ide u suprotnom smjeru u odnosu na sistem u cjelini (odnosno od izlaza do ulaza) naziva se povratna sprega sa prijenosnom funkcijom W os. U ovom slučaju, za negativan OS:
y = W p u; y 1 = W os y; u = y o - y 1 ,
Shodno tome
y = W p y o - W p y 1 = W p y o - W p W oc y = >
y(1 + W p W oc) = W p y o = > y = W eq y o ,
gdje  .
.
Slično:  - za pozitivan OS.
- za pozitivan OS.

Ako a Woc = 1, tada se povratna sprega naziva jedinica (slika 6b), tada W equiv \u003d W p / (1 ± W p).
Zatvoreni sistem se naziva jednostruka ako se, kada se otvori u bilo kojoj tački, dobije lanac serijski povezanih elemenata (slika 7a).

Dio kola, koji se sastoji od serijski povezanih karika, povezuje tačku primjene ulaznog signala sa tačkom uklanjanja izlaznog signala naziva se ravno kolo (slika 7b, prijenosna funkcija direktnog kola W p \u003d Wo W 1 W 2). Lanac serijski povezanih karika uključenih u zatvoreno kolo naziva se otvoreni krug(Sl. 7c, funkcija prijenosa otvorenog kruga W p = W 1 W 2 W 3 W 4). Na osnovu gornjih metoda ekvivalentne transformacije blok dijagrama, sistem sa jednom petljom može se predstaviti jednom vezom sa funkcijom prijenosa: W equiv \u003d W p / (1 ± W p)- prijenosna funkcija jednostrukog zatvorenog sistema s negativnom povratnom spregom jednaka je prijenosnoj funkciji prednjeg kola podijeljenoj s jedan plus prijenosnoj funkciji otvorenog kola. Za pozitivan OS, nazivnik ima predznak minus. Ako promijenite točku uklanjanja izlaznog signala, tada se mijenja oblik direktnog kola. Dakle, ako uzmemo u obzir izlazni signal y 1 na izlazu veze W 1, onda W p = Wo W 1. Izraz za funkciju prijenosa otvorenog kruga je nezavisan od točke u kojoj se uzima izlazni signal.

Zatvoreni sistemi su jednostruka i multiloop(Slika 8) Da biste pronašli ekvivalentnu prijenosnu funkciju za dano kolo, prvo morate transformirati pojedinačne sekcije.

Ako sistem sa više petlji ima unakrsne veze(Slika 9), tada su potrebna dodatna pravila za izračunavanje ekvivalentne funkcije prijenosa:
4. Prilikom prenosa sabirača preko veze duž signalne putanje potrebno je dodati vezu sa prijenosnom funkcijom veze preko koje se sabirač prenosi. Ako se sabirač prenosi na putanju signala, tada se dodaje veza sa prijenosnom funkcijom, inverzna prijenosna funkcija veze preko koje prenosimo sabirač (slika 10).

Dakle, signal se uzima sa izlaza sistema na slici 10a
y 2 = (f + y o W 1)W 2 .
Isti signal treba uzeti sa izlaza sistema na slici 10b:
y 2 \u003d fW 2 + y o W 1 W 2 = (f + y o W 1)W 2,
i na sl.10c:
y 2 = (f(1/W 1) + y o)W 1 W 2 = (f + y o W 1)W 2 .
S takvim transformacijama mogu se pojaviti neekvivalentni dijelovi komunikacijske linije (oni su zasjenjeni na slikama).

5. Prilikom prijenosa čvora preko veze duž putanje signala, dodaje se veza sa prijenosnom funkcijom, inverznom prijenosnom funkcijom veze preko koje prenosimo čvor. Ako se čvor prenosi prema putanji signala, tada se dodaje veza sa funkcijom prijenosa veze preko koje se čvor prenosi (slika 11). Dakle, signal se uzima sa izlaza sistema na slici 11a
y 1 = y o W 1 .
Isti signal se uzima sa izlaza na slici 11b:
y 1 = y o W 1 W 2 / W 2 = y o W 1
y 1 = y o W 1 .
6. Moguće su međusobne permutacije čvorova i sabirača: čvorovi se mogu zamijeniti (slika 12a); sabirci se takođe mogu zameniti (slika 12b); pri prenosu čvora kroz sabirač potrebno je dodati element za upoređivanje (slika 12c: y \u003d y 1 + f 1 \u003d\u003e y 1 \u003d y - f 1) ili zbrajalica (slika 12d: y = y1 + f1).

U svim slučajevima prenosa elemenata blok dijagrama postoje neekvivalentne regije komunikacionih linija, tako da morate biti oprezni na mjestima gdje se prima izlazni signal.
Uz ekvivalentne transformacije istog blok dijagrama, mogu se dobiti različite funkcije prijenosa sistema za različite ulaze i izlaze.
Laboratorija 4
Zakoni regulative
Neka je zadan neki ACS (slika 3).

Zakon regulacije je matematička zavisnost, prema kojoj bi kontrolno djelovanje na objekt proizvelo neinercijalni regulator.
Najjednostavniji od njih je proporcionalni zakon regulacije, pri čemu
u(t) = Ke(t)(sl. 4a),
gdje u(t) je kontrolna akcija koju generiše regulator, e(t)- odstupanje kontrolisane vrednosti od tražene vrednosti, K- koeficijent proporcionalnosti regulatora R.

Odnosno, da bi se stvorila kontrolna radnja, potrebno je imati kontrolnu grešku i da vrijednost ove greške bude proporcionalna remetećem efektu f(t). Drugim rečima, ACS kao celina treba da bude statičan.
Ovi regulatori se nazivaju P-regulatori.
Pošto kada smetnja utiče na objekat upravljanja, kontrolisana varijabla odstupa od tražene vrednosti konačnom brzinom (slika 4b), u početnom trenutku se na ulaz regulatora primenjuje veoma mala vrednost e, što izaziva slaba dejstva upravljanja u. Da bi se povećala brzina sistema, poželjno je forsirati proces upravljanja.
Da bi se to postiglo, u kontroler se uvode veze koje na izlazu formiraju signal proporcionalan derivatu ulazne vrijednosti, odnosno diferencirajuće ili forsirajuće veze.
Takav propis se zove o
KONSTRUKTIVNE SHEME LINIJA ACS
Tipične veze linearnog ACS-a
Svaki složeni ACS može se predstaviti kao skup više jednostavnih elemenata(zapamti funkcionalan i blok dijagrami). Stoga, da bi se pojednostavilo proučavanje procesa u stvarni sistemi predstavljeni su kao set idealizovane šeme, koji su tačno opisani matematički i približno okarakterisati stvarne veze sistema u određenom opsegu signalnih frekvencija.
Prilikom kompajliranja blok dijagrami neki tipične elementarne veze(jednostavna, dalje nedjeljiva), koju karakteriziraju samo njihove prijenosne funkcije, bez obzira na njihov dizajn, namjenu i princip rada. Razvrstajte ih prema vrsti jednačine opisujući njihov rad. U slučaju linearnog ACS-a razlikuju se sljedeće vrste veza:
1. Opisano linearnim algebarskim jednadžbama u odnosu na izlazni signal:
a) proporcionalan(statične, bez inercije);
b) odloženo.
2. Opisano diferencijalnim jednadžbama prvog reda sa konstantnim koeficijentima:
a) razlikovanje;
b) inercijalno-diferencirajući(stvarno razlikovanje);
u) inercijalni(aperiodično);
G) integrišući(astatična);
e) integro-diferencirajući(elastična).
3. Opisano diferencijalnim jednadžbama drugog reda s konstantnim koeficijentima:
a) inercijalna karika drugog reda(aperiodična veza drugog reda, oscilatorna).
Uzmite u obzir gore opisani matematički aparat prijenosne funkcije, prelazni i pulsni prolazni(po težini) karakteristike, kao i frekvencijske karakteristike ove veze.
Evo formula koje će se koristiti u tu svrhu.
1. Funkcija prijenosa: .
2. Odgovor na korak: ![]() .
.
3. : ili ![]() .
.
4. KCHH: .
5. Amplitudni frekvencijski odziv: ,
gdje ![]() ,
, ![]() .
.
6. Fazni frekventni odziv:  .
.
Prema ovoj šemi proučavamo tipične veze.
Imajte na umu da iako za neke tipične veze n(red izvedenice izlazni parametar na lijevoj strani jednačine) jednako m(red izvedenice ulazni parametar na desnoj strani jednačine), ne više m, kao što je ranije pomenuto, međutim, kada se konstruiše pravi ACS iz ovih veza, uslov m
proporcionalan(statički , bez inercije ) veza . Ovo je najjednostavnije veza, izlazni signalšto je direktno proporcionalno ulazni signal:
gdje k- koeficijent proporcionalnosti ili prijenos veze.
Primjeri takve veze su: a) ventili sa linearizovano karakteristike (kada se promijeni protok fluida proporcionalno stepenu promene položaj stabljike) u gornjim primjerima upravljačkih sistema; b) razdjelnik napona; c) poluga, itd.
Prelazeći u (3.1) na slike, imamo:
1. Funkcija prijenosa: .
2. Odgovor na korak: , Shodno tome .
3. impulsni odgovor: ![]() .
.
4. KCHH: .
6. PFC: ![]() .
.
Prihvaćen opis odnosa između ulaz i izlaz važi samo za savršena veza i odgovara stvarne veze samo kada niske frekvencije, . Kada su u stvarnim vezama, koeficijent prijenosa k počinje ovisiti o frekvenciji i visoke frekvencije pada na nulu.
zaostala veza. Ova veza je opisana jednadžbom
gdje je vrijeme kašnjenja.
Primjer zaostala veza opslužuju: a) duge električne vodove bez gubitaka; b) dugačak cjevovod, itd.
Funkcija prijenosa, prelazni i pulsni prolazni karakteristika, CFC, kao i frekvencijski odziv i fazni odziv ovog linka:
2. znači: .
Slika 3.1 prikazuje: a) KCHH hodograf zaostala veza; b) AFC i PFC retardirane veze. Imajte na umu da kada se povećava, kraj vektora opisuje ugao koji se stalno povećava u smjeru kazaljke na satu.

Sl.3.1. Hodograf (a) i AFC, PFC (b) retardirane veze.
Integrirajuća veza. Ova veza je opisana jednadžbom

gdje je koeficijent prijenosa veze.
Primjeri realnih elemenata čija su ekvivalentna kola svedena na integrator, su: a) električni kondenzator, ako uzmemo u obzir ulazni signal struja, i vikend- napon na kondenzatoru:  ; b) rotirajuća osovina, ako računate ulazni signal ugaona brzina rotacije, a izlaz - ugao rotacije osovine:
; b) rotirajuća osovina, ako računate ulazni signal ugaona brzina rotacije, a izlaz - ugao rotacije osovine:  ; itd.
; itd.
Hajde da definišemo karakteristike ovog linka:
2. ![]() .
.
Koristimo tablicu Laplaceove transformacije 3.1, dobijamo:
![]() .
.
Množimo s obzirom da je funkcija na .
3. ![]() .
.
4.  .
.
Slika 3.2 prikazuje: a) hodograf CFC integrirajuće veze; b) frekvencijski odziv i fazni odziv veze; c) prolazni odgovor veze.

Sl.3.2. Hodograf (a), frekvencijski odziv i fazni odziv (b), prolazni odziv (c) integrirajuće veze.
Veza za razlikovanje. Ova veza je opisana jednadžbom
gdje je koeficijent prijenosa veze.
Pronađimo karakteristike linka:
2. ![]() , s obzirom na to , nalazimo: .
, s obzirom na to , nalazimo: .
3. ![]() .
.
4. ![]() .
.
Slika 3.3 prikazuje: a) hodograf veze; b) frekvencijski odziv i fazni odziv veze.

a) b)
Rice. 3.3. Hodograf (a), frekvencijski odziv i fazni odziv (b) diferencirajuće veze.
Primjer diferencirajuća veza su idealan kondenzator i induktivnost. Ovo proizilazi iz činjenice da je napon u i struja i vezano za kondenzator OD i induktivnost L prema sljedećim odnosima:
Zapiši to stvarni kapacitet ima mali kapacitivna induktivnost, stvarna induktivnost Ima interturn kapacitivnost(koje su posebno izražene na visokim frekvencijama), što gornje formule dovodi do sljedećeg oblika:
![]() ,
, ![]() .
.
Na ovaj način, diferencijator ne može biti tehnički implementiran, jer red desna strana njegove jednačine (3.4) veća je od reda lijeve strane. A znamo da uslov mora biti zadovoljen n>m ili, u najmanju ruku, n=m.
Međutim, može se pristupiti ovoj jednačini veza, koristeći inercijalno-diferencirajući(stvarno razlikovanje)veza.
Inercijalno-diferencirajući(stvarno razlikovanje ) veza je opisana jednadžbom:
gdje k- koeficijent prijenosa linka, T- vremenska konstanta.
Funkcija prijenosa, prelazni i impulsni odgovor, CFC, AFC i PFC ove veze određene su formulama:
Koristimo svojstvo Laplaceove transformacije - pomeranje slike(3.20), prema kojem: ako , onda .
Odavde: ![]() .
.
3. ![]() .
.
5.  .
.
6. ![]() .
.
Slika 3.4 prikazuje: a) CFC grafikon; b) frekvencijski odziv i fazni odziv veze.

a) b)
Sl.3.4. Hodograf (a), frekvencijski odziv i fazni odziv stvarne diferencirajuće veze.
Kako bi za nekretnine pravi diferencijator u blizini imanja idealan, potrebno je istovremeno povećati koeficijent prijenosa k i smanjiti vremensku konstantu T tako da njihov proizvod ostane konstantan:
kT= k d,
gdje k e je koeficijent prijenosa diferencirajuće veze.
To pokazuje da u dimenziji koeficijenta prijenosa k d diferencirajuća veza uključeno vrijeme.
Inercijalna karika prvog reda(aperiodična veza ) je jedan od najčešćih linkovi ACS. Opisuje se jednačinom:
gdje k– koeficijent prijenosa linka, T je vremenska konstanta.
Karakteristike ove veze određene su formulama:
2. ![]() .
.
Korištenje svojstava integracija originala i pomeranje slike imamo:
 .
.
3.  , jer
, jer  na , tada je na cijeloj vremenskoj osi ova funkcija jednaka 0 (at ).
na , tada je na cijeloj vremenskoj osi ova funkcija jednaka 0 (at ).
5.  .
.
6. ![]() .
.
Slika 3.5 prikazuje: a) CFC grafikon; b) frekvencijski odziv i fazni odziv veze.

Sl.3.5. Hodograf (a), frekvencijski odziv i fazni odziv inercijalne karike prvog reda.
Integro-diferencirajuća veza. Ova veza je opisana diferencijalnom jednadžbom prvog reda u najopćenitijem obliku:
gdje k- koeficijent prijenosa linka, T 1 i T 2- vremenske konstante.
Hajde da uvedemo notaciju:
Ovisno o vrijednosti t veza će imati drugačija svojstva. Ako onda veza njegova svojstva će se približiti integrišući i inercijalni linkovi. Ako , onda dato veza nekretnine će biti bliže razlikovanje i inercijalno-diferencirajući.
Hajde da definišemo karakteristike integro-diferencirajuća veza:
1. ![]() .
.
2. ![]() , ovo implicira:
, ovo implicira:
Jer ![]() at t® 0, tada:
at t® 0, tada:
![]() .
.
6. ![]() .
.
Na sl.3.6. dato: a) CFC grafikon; b) frekvencijski odziv; c) PFC; d) prolazni odgovor veze.

a) b)

in) G)
Sl.3.6. Hodograf (a), frekvencijski odziv (b), fazni odziv (c), prolazni odziv (d) integrodiferencirajuće veze.
Inercijalna karika drugog reda. Ova veza je opisana diferencijalnom jednadžbom drugog reda:
gdje je (kapa) konstanta prigušenja; T- vremenska konstanta, k- koeficijent prijenosa veze.
Reakcija sistema opisanog jednačinom (3.8) na jednostepeno djelovanje na je prigušene harmonijske oscilacije, u ovom slučaju link se također poziva oscilatorno . Kada se vibracije ne pojave, i veza opisana jednačinom (3.8) se zove aperiodična veza drugog reda . Ako je , tada će oscilacije biti neprigušeni sa frekvencijom.
Primjer konstruktivne implementacije ovoga veza može poslužiti kao: a) električno oscilatorno kolo koje sadrži kapacitet, induktivnost i ohmic otpor; b) težina suspendovan na proljeće i imati uređaj za prigušivanje, itd.
Hajde da definišemo karakteristike inercijalna karika drugog reda:
1. ![]() .
.
2. ![]() .
.
Korijeni karakteristične jednadžbe u nazivniku određeni su:
![]() .
.
Očigledno, ovdje postoje tri moguća slučaja:
1) za korijene karakteristične jednačine negativan pravi razno i , tada je prolazni odgovor određen:
 ;
;
2) za korijene karakteristične jednačine negativne realne vrijednosti su iste ![]() :
:
3) na , korijeni karakteristične jednadžbe veze su kompleks-konjugirani ![]() , i
, i
prelazni odziv je određen formulom:
 ,
,
tj., kao što je gore navedeno, stiče oscilatornog karaktera.
3. Imamo i tri slučaja:
1) ![]() ,
,
jer  at ;
at ;
2) , jer at ;
3) ![]() , jer
, jer  u .
u .
5.  .
.
1.3.1 Karakteristike klasifikacije ACS veza Glavni zadatak teorije automatskog upravljanja TAU je da razvije metode pomoću kojih bi bilo moguće pronaći ili proceniti indikatore kvaliteta dinamičkih procesa u ACS. Drugim riječima, ne razmatraju se sva fizička svojstva elemenata sistema, već samo ona koja utiču, povezana su sa vrstom dinamičkog procesa. Ne uzimaju se u obzir konstruktivni dizajn elementa, njegove ukupne dimenzije, način sažimanja.
energija, karakteristike dizajna, raspon korištenih materijala itd. Međutim, bitni će parametri kao što su masa, moment inercije, toplinski kapacitet, kombinacije RC, LC itd., koji direktno određuju vrstu dinamičkog procesa. Osobine fizičkih performansi elementa važne su samo u onoj mjeri u kojoj će utjecati na njegovu dinamičku izvedbu. Dakle, razmatra se samo jedno odabrano svojstvo elementa - priroda njegovog dinamičkog procesa. Ovo nam omogućava da svedemo razmatranje fizičkog elementa na njegov dinamički model u obliku matematičkog modela. Modelsko rješenje, tj. Diferencijalna jednačina koja opisuje ponašanje elementa daje dinamički proces koji podliježe kvalitativnoj ocjeni.
Klasifikacija elemenata ACS-a nije zasnovana na karakteristikama dizajna ili karakteristikama njihove funkcionalne namene (upravljački objekat, uporedni element, regulatorno telo, itd.), već na vrsti matematičkog modela, tj. matematičke jednačine veze između izlaznih i ulaznih varijabli elementa. Štaviše, ova veza se može specificirati i u obliku diferencijalne jednadžbe i u drugom transformiranom obliku, na primjer, korištenjem prijenosnih funkcija (PF). Diferencijalna jednačina pruža sveobuhvatne informacije o svojstvima veze. Nakon što ga riješimo, s ovim ili onim datim zakonom ulazne vrijednosti, dobijamo reakciju po čijem obliku procjenjujemo svojstva elementa.
Uvođenje koncepta prijenosne funkcije omogućava dobivanje veze između izlaznih i ulaznih veličina u obliku operatora i istovremeno korištenje nekih svojstava prijenosne funkcije, što omogućava značajno pojednostavljenje matematičkog prikaza. sistema i koriste neka njihova svojstva. Da biste objasnili koncept PF, razmotrite neka svojstva Laplaceove transformacije.
1.3.2 Neka svojstva Laplasove transformacije Rešenje modela dinamičkih veza ACS-a daje promenu varijabli u vremenskoj ravni. Bavimo se funkcijama. X(t). Međutim, koristeći Laplaceovu transformaciju, mogu se transformirati u funkcije [X(p)] sa drugačijim argumentom p i novim svojstvima.
Laplaceova transformacija je poseban slučaj podudaranja tipa: jedna funkcija je povezana s drugom funkcijom. Obje funkcije su međusobno povezane određenom zavisnošću. Prepiska liči na ogledalo, na drugačiji način, u zavisnosti od forme, odražava predmet ispred sebe. Vrsta prikaza (korespondencija) može se birati proizvoljno, u zavisnosti od problema koji se rešava. Možete, na primjer, tražiti korespondenciju između skupa brojeva, čije se značenje svodi na to kako, prema odabranom broju at iz regiona Y pronađi broj X iz regiona x. Takav odnos se može specificirati analitički, u obliku tabele, grafikona, pravila itd.
Slično, može se uspostaviti korespondencija između grupa funkcija (slika 3.1 a), na primjer, u obliku:
Kao korespondencija između funkcija x(t) i x(p) (slika 3.1 b), može se koristiti Laplaceov integral:
pod uslovima: x(t)= 0 na i na t.
U ACS-u se ne istražuju apsolutne promjene varijabli, već njihova odstupanja od vrijednosti stabilnog stanja. shodno tome, x(t) - klasa funkcija koje opisuju odstupanja varijabli u sistemu automatskog upravljanja i za njih su zadovoljena oba uslova Laplaceove transformacije: prvi - budući da nema promjene varijabli prije primjene perturbacije, drugi - budući da tokom vremena svako odstupanje u operativnom sistemu teži nuli.
Ovo su uslovi za postojanje Laplaceovog integrala. Uzmimo, kao primjer, slike najjednostavnijih funkcija ali do Laplacea.
Rice. 3.1. Tipovi prikaza funkcija
Dakle, ako je data jedinična funkcija x(t) = 1, onda
Za eksponencijalnu funkciju x(t) = e -α t, slika by
Laplace će izgledati ovako:
konačno:
Rezultirajuće funkcije nisu ništa kompliciranije od originalnih. Funkcija x(t) se zove original, i x(p)- njen imidž. Uslovno direktna i inverzna Laplaceova transformacija može se predstaviti kao:
L=x(p),L -1<=x(t).
U ovom slučaju postoji nedvosmislen odnos između originala i slike, i obrnuto, jedina slika funkcije odgovara originalu. Razmotrite neka svojstva Laplaceove transformacije.
Slika diferencijala funkcija. Neka funkcija x(t) odgovara slici x(p): x(t)-> x(p)- Potrebno je pronaći sliku njegovog derivata x(t):
Na ovaj način
Pod nultim početnim uslovima
Za sliku derivacije n-tog reda:
Dakle, slika derivacije funkcije je slika same funkcije, pomnožena sa operatorom str u meri u kojoj n, gdje P je red diferencijacije.
Elementarna dinamička veza (EDZ) naziva se matematički model elementa u obliku diferencijalne jednadžbe koja ne podliježe daljem pojednostavljenju.
1.3.3 Inercijalna aperiodična veza prvog reda
Takva veza je opisana diferencijalnom jednadžbom prvog reda koja povezuje ulazne i izlazne veličine:
Primjer takve karike, pored termoelementa, DC motora, RL lanca, može biti i pasivni RC- lanac (slika 3.2 d).
Koristeći osnovne zakone za opisivanje električnih kola, dobijamo matematički model aperiodične veze u diferencijalnom obliku:
Dobijmo odnos između ulaznih i izlaznih vrijednosti veze u obliku Laplaceove transformacije:
Rice. 3.2. Primjeri aperiodičnih veza
Omjer izlazne vrijednosti i ulazne vrijednosti daje operator oblika.