Penyelesaian pertidaksamaan trigonometri. Pertidaksamaan trigonometri dan solusinya Contoh pertidaksamaan trigonometri kompleks

Kementerian Pendidikan Republik Belarus

lembaga pendidikan

"Universitas Negeri Gomel

dinamai Francysk Skaryna"

Fakultas Matematika

Jurusan Aljabar dan Geometri

Layak untuk pertahanan

Kepala Departemen Shemetkov L.A.

Persamaan dan pertidaksamaan trigonometri

Tugas kursus

Pelaksana:

kelompok siswa M-51

CM. Gorsky

Penasihat ilmiah

Dosen senior

V.G. Safonov

Gomel 2008

PENGANTAR

METODE DASAR UNTUK MENYELESAIKAN PERSAMAAN TRIGONOMETRI

Faktorisasi

Menyelesaikan persamaan dengan mengubah produk fungsi trigonometri menjadi jumlah

Menyelesaikan Persamaan Menggunakan Rumus Argumen Tiga

Perkalian dengan beberapa fungsi trigonometri

PERSAMAAN TRIGONOMETRI NON-STANDAR

PERTIMBANGAN TRIGONOMETRI

PILIHAN AKAR

TUGAS UNTUK SOLUSI INDEPENDEN

KESIMPULAN

DAFTAR SUMBER YANG DIGUNAKAN

Pada zaman kuno, trigonometri muncul sehubungan dengan kebutuhan astronomi, survei dan konstruksi, yaitu, itu murni geometris dan diwakili terutama<<исчисление хорд>>. Seiring waktu, beberapa titik analitis mulai menyelingi ke dalamnya. Pada paruh pertama abad ke-18 ada belokan tajam, setelah itu trigonometri mengambil arah baru dan bergeser ke arah analisis matematis. Pada saat inilah ketergantungan trigonometri mulai dianggap sebagai fungsi.

Persamaan trigonometri adalah salah satu topik yang paling sulit dalam kursus matematika sekolah. Persamaan trigonometri muncul ketika memecahkan masalah dalam planimetri, geometri padat, astronomi, fisika, dan bidang lainnya. Persamaan trigonometri dan ketidaksetaraan dari tahun ke tahun ditemukan di antara tugas-tugas pengujian terpusat.

Perbedaan paling penting antara persamaan trigonometri dan aljabar adalah bahwa persamaan aljabar memiliki jumlah akar yang terbatas, sedangkan persamaan trigonometri memiliki jumlah tak terbatas, yang sangat memperumit pemilihan akar. Kekhususan lain dari persamaan trigonometri adalah bentuk penulisan jawaban yang tidak unik.

Tesis ini dikhususkan untuk metode penyelesaian persamaan dan pertidaksamaan trigonometri.

Pekerjaan diploma terdiri dari 6 bagian.

Bagian pertama berisi informasi teoritis dasar: definisi dan sifat-sifat trigonometri dan fungsi trigonometri terbalik; tabel nilai fungsi trigonometri untuk beberapa argumen; ekspresi fungsi trigonometri dalam hal fungsi trigonometri lainnya, yang sangat penting untuk mengubah ekspresi trigonometri, terutama yang mengandung invers fungsi trigonometri; selain yang utama rumus trigonometri, yang terkenal dari kursus sekolah, adalah rumus yang menyederhanakan ekspresi yang mengandung fungsi trigonometri terbalik.

Bagian kedua menguraikan metode utama untuk memecahkan persamaan trigonometri. Solusi persamaan trigonometri dasar, metode pemfaktoran, metode pengurangan persamaan trigonometri menjadi persamaan aljabar dipertimbangkan. Mengingat fakta bahwa solusi persamaan trigonometri dapat ditulis dalam beberapa cara, dan bentuk solusi ini tidak memungkinkan seseorang untuk segera menentukan apakah solusi ini sama atau berbeda, yang dapat<<сбить с толку>> saat menyelesaikan tes, skema umum untuk menyelesaikan persamaan trigonometri dipertimbangkan dan transformasi grup solusi umum persamaan trigonometri dipertimbangkan secara rinci.

Bagian ketiga membahas persamaan trigonometri non-standar, yang penyelesaiannya didasarkan pada pendekatan fungsional.

Bagian keempat membahas pertidaksamaan trigonometri. Metode untuk memecahkan ketidaksetaraan trigonometri dasar dipertimbangkan secara rinci, seperti dalam lingkaran satuan serta metode grafis. Proses penyelesaian pertidaksamaan trigonometri non-dasar melalui pertidaksamaan dasar dan metode interval yang sudah dikenal oleh anak sekolah dijelaskan.

Bagian kelima menyajikan tugas yang paling sulit: ketika diperlukan tidak hanya untuk menyelesaikan persamaan trigonometri, tetapi juga untuk memilih akar dari akar yang ditemukan yang memenuhi beberapa kondisi. Bagian ini memberikan solusi untuk tugas-tugas khas untuk pemilihan akar. Informasi teoretis yang diperlukan untuk pemilihan akar diberikan: partisi himpunan bilangan bulat menjadi himpunan bagian yang tidak berpotongan, solusi persamaan dalam bilangan bulat (diophantine).

Bagian keenam menyajikan tugas untuk solusi mandiri dalam bentuk tes. 20 tugas tes mencantumkan tugas paling sulit yang dapat ditemui dalam pengujian terpusat.

Persamaan trigonometri dasar

Persamaan trigonometri dasar adalah persamaan yang berbentuk , dimana salah satu fungsi trigonometrinya adalah : , , , .

Persamaan trigonometri dasar memiliki banyak akar tak terhingga. Misalnya, nilai-nilai berikut memenuhi persamaan: , , , dll. Rumus umum yang digunakan untuk menemukan semua akar persamaan, di mana , adalah:

Di sini ia dapat mengambil nilai bilangan bulat apa pun, masing-masing sesuai dengan akar persamaan tertentu; dalam rumus ini (juga dalam rumus lain yang dengannya persamaan trigonometri dasar diselesaikan) disebut parameter. Mereka biasanya menuliskan, dengan demikian menekankan bahwa parameter dapat mengambil nilai integer apa pun.

Solusi dari persamaan , Dimana , ditemukan dengan rumus

Persamaan diselesaikan dengan menerapkan rumus

dan persamaan --- menurut rumus

Mari kita perhatikan secara khusus beberapa kasus khusus persamaan trigonometri dasar, ketika solusinya dapat ditulis tanpa menggunakan rumus umum:

Ketika memecahkan persamaan trigonometri, periode fungsi trigonometri memainkan peran penting. Oleh karena itu, kami menyajikan dua teorema yang berguna:

Dalil Jika --- periode utama dari fungsi tersebut, maka bilangan tersebut adalah periode utama dari fungsi tersebut.

Periode fungsi dan disebut sebanding jika ada bilangan asli dan , itu .

Dalil Jika fungsi periodik dan , memiliki persamaan dan , maka memiliki periode yang sama , yaitu periode dari fungsi , , .

Teorema mengatakan apa periode fungsi , , , dan belum tentu periode utama. Misalnya, periode utama dari fungsi dan adalah --- , dan periode utama produknya adalah --- .

Memperkenalkan Argumen Bantu

Cara standar untuk mengubah ekspresi bentuk adalah trik berikut: biarkan --- sudut yang diberikan oleh persamaan , . Untuk setiap dan sudut seperti itu ada. Lewat sini . Jika , atau , , , sebaliknya .

Skema untuk menyelesaikan persamaan trigonometri

Skema utama yang akan kita pandu saat menyelesaikan persamaan trigonometri adalah sebagai berikut:

larutan persamaan yang diberikan mengurangi untuk memecahkan persamaan dasar. Alat solusi --- transformasi, faktorisasi, perubahan yang tidak diketahui. Prinsip panduannya adalah jangan sampai kehilangan akar. Ini berarti bahwa ketika pindah ke persamaan (persamaan) berikutnya, kami tidak takut dengan munculnya akar tambahan (asing), tetapi kami hanya peduli bahwa setiap persamaan berikutnya dari "rantai" kami (atau satu set persamaan dalam kasus percabangan) adalah konsekuensi dari yang sebelumnya. Salah satu metode yang mungkin untuk memilih akar adalah untuk memeriksa. Kami segera mencatat bahwa dalam kasus persamaan trigonometri, kesulitan yang terkait dengan pemilihan akar, dengan verifikasi, sebagai suatu peraturan, meningkat tajam dibandingkan dengan persamaan aljabar. Lagi pula, Anda harus memeriksa seri, yang terdiri dari jumlah anggota yang tidak terbatas.

Perhatian khusus harus dibuat dari perubahan yang tidak diketahui dalam memecahkan persamaan trigonometri. Dalam kebanyakan kasus, setelah penggantian yang diperlukan, persamaan aljabar diperoleh. Selain itu, persamaan tidak begitu langka yang, meskipun dalam penampilan trigonometri, pada dasarnya tidak demikian, karena sudah setelah langkah pertama --- perubahan variabel --- berubah menjadi aljabar, dan kembali ke trigonometri hanya terjadi di atas panggung menyelesaikan persamaan trigonometri dasar.

Mari kita ingatkan sekali lagi: penggantian yang tidak diketahui harus dilakukan sesegera mungkin, persamaan yang diperoleh setelah penggantian harus diselesaikan sampai akhir, termasuk tahap pemilihan akar, dan baru kemudian akan kembali ke aslinya tidak dikenal.

Salah satu fitur persamaan trigonometri adalah bahwa jawabannya dalam banyak kasus dapat ditulis dalam berbagai cara. Bahkan untuk menyelesaikan persamaan jawabannya dapat ditulis seperti ini:

1) dalam bentuk dua seri: , , ;

2) dalam bentuk baku, yang merupakan gabungan dari deret di atas: , ;

3) sejak , maka jawabannya dapat ditulis sebagai , . (Selanjutnya, kehadiran parameter , , atau dalam catatan respons secara otomatis berarti bahwa parameter ini mengambil semua kemungkinan nilai integer. Pengecualian akan ditetapkan.)

Jelas, tiga kasus yang terdaftar tidak menghabiskan semua kemungkinan untuk menulis jawaban persamaan yang sedang dipertimbangkan (ada banyak dari mereka).

Misalnya untuk . Oleh karena itu, dalam dua kasus pertama, jika , kita dapat mengganti dengan .

Biasanya, jawabannya ditulis berdasarkan paragraf 2. Berguna untuk mengingat rekomendasi berikut: jika pekerjaan tidak berakhir dengan solusi persamaan, masih perlu melakukan studi, pemilihan akar, kemudian bentuk pencatatan yang paling nyaman ditunjukkan dalam paragraf 1. (Rekomendasi serupa harus diberikan untuk persamaan.)

Mari kita perhatikan sebuah contoh yang mengilustrasikan apa yang telah dikatakan.

Contoh Memecahkan persamaan.

Larutan. Yang paling jelas adalah cara berikut. Persamaan ini terbagi menjadi dua: dan . Memecahkan masing-masing dan menggabungkan jawaban yang diperoleh, kami menemukan .

Cara lain. Sejak , maka, menggantikan dan dengan rumus reduksi. Setelah transformasi kecil, kita mendapatkan , dari mana .

Sepintas, formula kedua tidak memiliki keunggulan khusus dibandingkan yang pertama. Namun, jika kita ambil, misalnya, , maka ternyata , yaitu. persamaan memiliki solusi, sedangkan cara pertama membawa kita ke jawabannya . "Lihat" dan buktikan kesetaraan tidak begitu mudah.

Menjawab. .

Transformasi dan penyatuan kelompok solusi umum persamaan trigonometri

Kami akan mempertimbangkan perkembangan aritmatika yang meluas tanpa batas di kedua arah. Suku-suku barisan ini dapat dibagi menjadi dua kelompok suku yang terletak di sebelah kanan dan di sebelah kiri suku tertentu, yang disebut suku tengah atau suku nol dari barisan tersebut.

Memperbaiki salah satu istilah dari perkembangan tak terbatas dengan angka nol, kita harus melakukan penomoran ganda untuk semua istilah yang tersisa: positif untuk istilah yang terletak di sebelah kanan, dan negatif untuk istilah yang terletak di sebelah kiri nol.

Dalam kasus umum, jika perbedaan dari barisan adalah suku nol, rumus untuk setiap suku (th) dari barisan aritmatika tak terbatas adalah:

Transformasi rumus untuk setiap anggota dari perkembangan aritmatika tak terbatas

1. Jika kita menambah atau mengurangi selisih dari perkembangan ke suku nol, maka perkembangan tidak akan berubah dari ini, tetapi hanya suku nol yang akan bergerak, mis. jumlah anggota akan berubah.

2. Jika koefisien suatu variabel dikalikan dengan , maka ini hanya akan menghasilkan permutasi dari anggota grup kanan dan kiri.

3. Jika anggota berturut-turut dari perkembangan tak terbatas

misalnya , , , ..., , untuk membuat suku-suku pusat dari barisan dengan selisih yang sama menjadi :

maka deret dan deret menunjukkan angka yang sama.

Contoh Baris dapat diganti dengan tiga baris berikut: , , .

4. Jika barisan tak hingga dengan selisih yang sama memiliki bilangan sebagai anggota pusat yang membentuk barisan aritmatika dengan selisih , maka barisan tersebut dapat diganti dengan satu barisan dengan selisih , dan dengan anggota pusat sama dengan salah satu anggota pusatnya progresi, yaitu jika

kemudian progresi ini digabungkan menjadi satu:

Contoh , , , keduanya digabungkan menjadi satu kelompok, karena .

Untuk mengubah grup yang memiliki solusi umum menjadi grup yang tidak memiliki solusi umum, grup ini didekomposisi menjadi grup dengan periode yang sama, dan kemudian kami mencoba menggabungkan grup yang dihasilkan, tidak termasuk grup berulang.

Faktorisasi

Metode faktorisasinya adalah sebagai berikut: jika

maka setiap solusi persamaan

adalah solusi dari himpunan persamaan

Pernyataan kebalikannya, secara umum, salah: tidak setiap solusi himpunan adalah solusi persamaan. Hal ini disebabkan fakta bahwa solusi persamaan individu mungkin tidak termasuk dalam domain definisi fungsi .

Contoh Memecahkan persamaan.

Larutan. Menggunakan identitas trigonometri dasar, kami mewakili persamaan dalam bentuk

Menjawab. ; .

Mengubah jumlah fungsi trigonometri menjadi produk

Contoh selesaikan persamaannya .

Larutan. Kami menerapkan rumus, kami memperoleh persamaan yang setara

Menjawab. .

Contoh Memecahkan persamaan.

Larutan. Dalam hal ini, sebelum menerapkan rumus untuk jumlah fungsi trigonometri, Anda harus menggunakan rumus pengurangan . Sebagai hasilnya, kami memperoleh persamaan yang setara

Menjawab. , .

Menyelesaikan persamaan dengan mengubah produk fungsi trigonometri menjadi jumlah

Saat memecahkan sejumlah persamaan, rumus digunakan.

Contoh selesaikan persamaannya

Larutan.

Menjawab. , .

Contoh Memecahkan persamaan.

Larutan. Menerapkan rumus, kami memperoleh persamaan yang setara:

Menjawab. .

Menyelesaikan Persamaan Menggunakan Rumus Pengurangan

Saat memecahkan berbagai persamaan trigonometri, rumus memainkan peran kunci.

Contoh Memecahkan persamaan.

Larutan. Menerapkan rumus, kami memperoleh persamaan yang setara.

Menjawab. ; .

Menyelesaikan Persamaan Menggunakan Rumus Argumen Tiga

Contoh Memecahkan persamaan.

Larutan. Kami menerapkan rumus, kami mendapatkan persamaan

Menjawab. ; .

Contoh selesaikan persamaannya .

Larutan. Menerapkan rumus untuk menurunkan derajat, kita mendapatkan: . Menerapkan kita mendapatkan:

Menjawab. ; .

Persamaan fungsi trigonometri dengan nama yang sama

Contoh Memecahkan persamaan.

Larutan.

Menjawab. , .

Contoh selesaikan persamaannya .

Larutan. Mari kita ubah persamaannya.

Menjawab. .

Contoh Diketahui bahwa dan memenuhi persamaan

Temukan jumlahnya.

Larutan. Ini mengikuti dari persamaan bahwa

Menjawab. .

Pertimbangkan jumlah formulir

Jumlah ini dapat dikonversi menjadi produk dengan mengalikan dan membaginya dengan , maka kita dapatkan

Teknik ini dapat digunakan untuk menyelesaikan beberapa persamaan trigonometri, tetapi harus diingat bahwa sebagai hasilnya, akar asing mungkin muncul. Berikut adalah generalisasi dari rumus-rumus tersebut:

Contoh Memecahkan persamaan.

Larutan. Dapat dilihat bahwa himpunan tersebut merupakan solusi dari persamaan semula. Oleh karena itu, mengalikan ruas kiri dan kanan persamaan dengan tidak akan menghasilkan akar tambahan.

Kita punya .

Menjawab. ; .

Contoh Memecahkan persamaan.

Larutan. Kami mengalikan sisi kiri dan kanan persamaan dengan dan menerapkan rumus untuk mengubah produk fungsi trigonometri menjadi jumlah, kami memperoleh

Persamaan ini setara dengan himpunan dua persamaan dan , dari mana dan .

Karena akar persamaan bukan akar persamaan, maka dari himpunan solusi yang dihasilkan harus dikeluarkan. Jadi di set Anda perlu mengecualikan .

Menjawab. dan , .

Contoh selesaikan persamaannya .

Larutan. Mari kita ubah ekspresinya:

Persamaan tersebut akan ditulis dalam bentuk:

Menjawab. .

Pengurangan persamaan trigonometri menjadi persamaan aljabar

Mengurangi menjadi persegi

Jika persamaan terlihat seperti

maka penggantinya membuatnya menjadi persegi, karena () dan.

Jika bukan istilahnya ada , maka penggantian yang dibutuhkan adalah .

persamaan

dikurangi menjadi persamaan kuadrat

presentasi sebagai . Sangat mudah untuk memeriksa yang , bukan akar persamaan, dan dengan membuat perubahan , persamaan direduksi menjadi kuadrat.

Contoh Memecahkan persamaan.

Larutan. Mari kita pindahkan ke sisi kiri, ganti dengan , dan ekspresikan melalui dan .

Setelah disederhanakan, kita mendapatkan: . Bagilah suku demi suku dengan , buat substitusinya :

Kembali ke , kita menemukan .

Persamaan homogen terhadap ,

Pertimbangkan persamaan bentuk

di mana , , , ..., , --- sah angka. Dalam setiap suku di ruas kiri persamaan, derajat monomialnya sama, yaitu, jumlah derajat sinus dan cosinusnya sama dan sama dengan. Persamaan seperti ini disebut homogen relatif terhadap dan , dan bilangan tersebut disebut indikator homogenitas .

Jelas bahwa jika , maka persamaan akan berbentuk:

yang solusinya adalah nilai-nilai yang , yaitu, angka , . Persamaan kedua, yang ditulis dalam tanda kurung, juga homogen, tetapi derajatnya 1 lebih rendah.

Jika , maka bilangan-bilangan ini bukan akar-akar persamaan.

Ketika kita mendapatkan: , dan ruas kiri persamaan (1) mengambil nilai .

Jadi, untuk , Dan , Oleh karena itu, kedua ruas persamaan dapat dibagi . Akibatnya, kita mendapatkan persamaan:

yang, dengan substitusi, mudah direduksi menjadi aljabar:

Persamaan homogen dengan indeks homogenitas 1. Pada , kita memiliki persamaan .

Jika , maka persamaan ini ekuivalen dengan persamaan , , dari mana , .

Contoh Memecahkan persamaan.

Larutan. Persamaan ini homogen derajat pertama. Membagi kedua bagiannya dengan kita mendapatkan: , , , .

Menjawab. .

Contoh Di , kita memperoleh persamaan homogen dalam bentuk

Larutan.

Jika , maka kita membagi kedua sisi persamaan dengan , kita mendapatkan persamaan , yang dapat dengan mudah direduksi menjadi persegi dengan substitusi: . Jika sebuah , maka persamaan tersebut memiliki akar real , . Persamaan asli akan memiliki dua kelompok solusi: , , .

Jika sebuah , maka persamaan tersebut tidak memiliki solusi.

Contoh Memecahkan persamaan.

Larutan. Persamaan ini homogen derajat kedua. Membagi kedua sisi persamaan dengan , kita mendapatkan: . Biarkan , maka , , . , , ; , , .

Menjawab. .

Persamaan direduksi menjadi persamaan bentuk

Untuk melakukan ini, cukup menggunakan identitas

Secara khusus, persamaan direduksi menjadi persamaan homogen jika diganti dengan , maka kita mendapatkan persamaan ekivalen:

Contoh Memecahkan persamaan.

Larutan. Mari kita ubah persamaan menjadi persamaan homogen:

Bagilah kedua ruas persamaan dengan , kita mendapatkan persamaan:

Membiarkan , maka kita sampai pada persamaan kuadrat: , , , , .

Menjawab. .

Contoh Memecahkan persamaan.

Larutan. Mari kita kuadratkan kedua sisi persamaan, mengingat keduanya memiliki nilai positif: , ,

Biarkan , maka kita dapatkan , , .

Menjawab. .

Persamaan Dipecahkan Menggunakan Identitas

Hal ini berguna untuk mengetahui rumus berikut:

Contoh Memecahkan persamaan.

Larutan. Menggunakan, kita mendapatkan

Menjawab.

Kami tidak menawarkan formula itu sendiri, tetapi cara untuk memperolehnya:

Akibatnya,

Juga, .

Contoh selesaikan persamaannya .

Larutan. Mari kita ubah ekspresinya:

Persamaan tersebut akan ditulis dalam bentuk:

Mengambil , kita mendapatkan . , . Akibatnya

Menjawab. .

Substitusi trigonometri universal

Persamaan trigonometri bentuk

di mana --- rasional fungsi dengan bantuan rumus -- , serta dengan bantuan rumus -- dapat direduksi menjadi persamaan rasional sehubungan dengan argumen , , , setelah itu persamaan tersebut dapat direduksi menjadi persamaan rasional aljabar sehubungan untuk menggunakan rumus substitusi trigonometri universal

Perlu dicatat bahwa penggunaan rumus dapat menyebabkan penyempitan ODZ dari persamaan asli, karena tidak ditentukan pada titik , jadi dalam kasus seperti itu perlu untuk memeriksa apakah sudut adalah akar dari persamaan asli .

Contoh Memecahkan persamaan.

Larutan. Sesuai dengan tugas. Menerapkan rumus dan membuat substitusi , kita dapatkan

dari mana dan, oleh karena itu, .

persamaan bentuk

Persamaan bentuk , dimana --- polinomial, diselesaikan dengan mengubah yang tidak diketahui

Contoh Memecahkan persamaan.

Larutan. Dengan melakukan substitusi dan dengan mempertimbangkan , kita peroleh

di mana , . --- akar asing, karena . akar persamaan adalah .

Penggunaan Fungsi Terbatas

Dalam praktek pengujian terpusat, tidak jarang dijumpai persamaan yang penyelesaiannya didasarkan pada keterbatasan fungsi dan . Sebagai contoh:

Contoh Memecahkan persamaan.

Larutan. Karena , , maka ruas kiri tidak melebihi dan sama dengan , jika

Untuk menemukan nilai yang memenuhi kedua persamaan, kami melanjutkan sebagai berikut. Kami memecahkan salah satunya, lalu di antara nilai-nilai yang ditemukan kami memilih yang memenuhi yang lain.

Mari kita mulai dengan yang kedua: , . Kemudian , .

Jelas bahwa hanya untuk bilangan genap akan .

Menjawab. .

Ide lain diwujudkan dengan memecahkan persamaan berikut:

Contoh selesaikan persamaannya .

Larutan. Mari kita gunakan properti dari fungsi eksponensial: , .

Menambahkan ketidaksetaraan ini istilah demi istilah, kami memiliki:

Oleh karena itu, ruas kiri persamaan ini sama jika dan hanya jika kedua persamaan berlaku:

yaitu dapat mengambil nilai , , , atau dapat mengambil nilai , .

Menjawab. , .

Contoh selesaikan persamaannya .

Larutan., . Akibatnya, .

Menjawab. .

Contoh selesaikan persamaannya

Larutan. Nyatakan , maka dari definisi fungsi trigonometri terbalik kita memiliki dan .

Karena , pertidaksamaan mengikuti dari persamaan, yaitu. . Sejak dan , maka dan . Namun, dan karena itu.

Jika dan , maka . Karena sebelumnya telah ditetapkan bahwa , maka .

Menjawab. , .

Contoh selesaikan persamaannya

Larutan. Rentang nilai persamaan yang valid adalah .

Mari kita tunjukkan terlebih dahulu bahwa fungsi

Untuk apa pun, itu hanya dapat mengambil nilai positif.

Mari kita nyatakan fungsinya sebagai berikut: .

Sejak , maka , yaitu, .

Oleh karena itu, untuk membuktikan pertidaksamaan , perlu ditunjukkan bahwa . Untuk tujuan ini, kita kubus kedua bagian dari ketidaksetaraan ini, maka

Pertidaksamaan numerik yang dihasilkan menunjukkan bahwa . Jika kita juga memperhitungkan bahwa , maka ruas kiri persamaan adalah non-negatif.

Pertimbangkan sekarang sisi kanan persamaan.

Karena , kemudian

Namun, diketahui bahwa . Ini mengikuti dari sini bahwa , yaitu. sisi kanan persamaan tidak melebihi . Sebelumnya, telah dibuktikan bahwa ruas kiri persamaan adalah non-negatif, oleh karena itu, persamaan dalam hanya dapat terjadi jika kedua bagiannya sama, dan ini hanya mungkin untuk .

Menjawab. .

Contoh selesaikan persamaannya

Larutan. Tunjukkan dan . Menerapkan ketidaksetaraan Cauchy-Bunyakovsky, kami memperoleh . Oleh karena itu berikut ini . Di sisi lain, ada . Oleh karena itu, persamaan tidak memiliki akar.

Menjawab. .

Contoh Selesaikan persamaan:

Larutan. Mari kita tulis ulang persamaan dalam bentuk:

Menjawab. .

Metode fungsional untuk menyelesaikan persamaan trigonometri dan gabungan

Tidak setiap persamaan sebagai hasil transformasi dapat direduksi menjadi persamaan satu atau lain bentuk standar, yang memiliki metode penyelesaian tertentu. Dalam kasus seperti itu, ternyata berguna untuk menggunakan sifat-sifat fungsi seperti itu dan sebagai monotonisitas, keterbatasan, kemerataan, periodisitas, dll. Jadi, jika salah satu fungsi berkurang, dan yang kedua meningkat pada interval, maka jika persamaan memiliki akar pada interval ini, akar ini unik, dan kemudian, misalnya, dapat ditemukan dengan seleksi. Jika fungsi dibatasi dari atas, dan , dan fungsi dibatasi dari bawah, dan , maka persamaan tersebut ekuivalen dengan sistem persamaan

Contoh selesaikan persamaannya

Larutan. Kami mengubah persamaan asli ke bentuk

dan menyelesaikannya sebagai persegi sehubungan dengan . Kemudian kita mendapatkan

Mari selesaikan persamaan himpunan pertama. Dengan mempertimbangkan keterbatasan fungsi , kita sampai pada kesimpulan bahwa persamaan hanya dapat memiliki akar pada interval . Pada interval ini, fungsi meningkat, dan fungsi menurun. Oleh karena itu, jika persamaan ini memiliki akar, maka persamaan tersebut unik. Kami menemukan melalui seleksi.

Menjawab. .

Contoh selesaikan persamaannya

Larutan. Biarkan , dan , maka persamaan aslinya dapat ditulis sebagai persamaan fungsional . Karena fungsinya ganjil, maka . Dalam hal ini, kita mendapatkan persamaan

Karena , Dan monoton pada , persamaan tersebut setara dengan persamaan , yaitu. , yang memiliki akar tunggal .

Menjawab. .

Contoh selesaikan persamaannya .

Larutan. Berdasarkan teorema turunan dari suatu fungsi kompleks, jelas bahwa fungsi menurun (fungsi menurun, meningkat, menurun). Dari sini jelas bahwa fungsi didefinisikan pada , menurun. Itu sebabnya persamaan yang diberikan memiliki paling banyak satu akar. Karena , kemudian

Menjawab. .

Contoh Memecahkan persamaan.

Larutan. Perhatikan persamaan pada tiga interval.

a) Biarkan . Kemudian pada himpunan ini persamaan awal ekuivalen dengan persamaan . Yang tidak memiliki solusi pada interval, karena , , sebuah . Pada interval, persamaan asli juga tidak memiliki akar, karena , sebuah .

b) Biarkan . Maka pada himpunan ini persamaan awal ekuivalen dengan persamaan

yang akar-akarnya pada interval adalah bilangan , , , .

c) Biarkan . Maka pada himpunan ini persamaan awal ekuivalen dengan persamaan

Yang tidak memiliki solusi pada interval, karena , tetapi . Persamaan juga tidak memiliki solusi pada interval, karena , , sebuah .

Menjawab. , , , .

Metode simetri

Lebih mudah menggunakan metode simetri ketika pernyataan tugas berisi persyaratan bahwa solusi persamaan, pertidaksamaan, sistem, dll. harus unik. atau indikasi yang tepat dari jumlah solusi. Dalam hal ini, simetri apa pun dari ekspresi yang diberikan harus dideteksi.

Penting juga untuk mempertimbangkan berbagai kemungkinan jenis simetri yang berbeda.

Sama pentingnya adalah ketaatan yang ketat dari tahapan logis dalam penalaran dengan simetri.

Biasanya, simetri memungkinkan kita untuk menetapkan hanya kondisi yang diperlukan, dan kemudian kita perlu memeriksa kecukupannya.

Contoh Temukan semua nilai parameter yang persamaannya memiliki solusi unik.

Larutan. Perhatikan bahwa dan --- bahkan fungsi, sehingga ruas kiri persamaan adalah fungsi genap.

Jadi jika --- solusi persamaan, yang juga merupakan solusi dari persamaan. Jika adalah satu-satunya solusi untuk persamaan, maka diperlukan , .

Ayo pilih mungkin nilai , yang mengharuskannya menjadi akar persamaan.

Kami segera mencatat bahwa nilai-nilai lain tidak dapat memenuhi kondisi masalah.

Namun belum diketahui apakah semua yang dipilih benar-benar memenuhi kondisi masalah.

Kecukupan.

1) , persamaan akan berbentuk .

2) , persamaan akan berbentuk:

Jelas, untuk semua dan . Oleh karena itu, persamaan terakhir setara dengan sistem:

Jadi, kami telah membuktikan bahwa untuk , persamaan memiliki solusi unik.

Menjawab. .

Solusi dengan eksplorasi fungsi

Contoh Buktikan bahwa semua solusi persamaan

bilangan bulat.

Larutan. Periode utama dari persamaan awal adalah . Oleh karena itu, pertama-tama kita mempelajari persamaan ini pada segmen .

Mari kita ubah persamaan menjadi bentuk:

Dengan bantuan kalkulator kita mendapatkan:

Jika , maka dari persamaan sebelumnya kita peroleh:

Memecahkan persamaan yang dihasilkan, kita mendapatkan: .

Perhitungan yang dilakukan memberikan kesempatan untuk mengasumsikan bahwa akar-akar persamaan yang termasuk dalam interval adalah , dan .

Verifikasi langsung mengkonfirmasi hipotesis ini. Dengan demikian, terbukti bahwa akar-akar persamaan hanya bilangan bulat , .

Contoh Selesaikan Persamaan .

Larutan. Temukan periode utama persamaan. Periode utama dari fungsi tersebut adalah . Periode utama dari fungsi tersebut adalah . Kelipatan persekutuan terkecil dari bilangan tersebut dan sama dengan . Oleh karena itu, periode utama persamaan tersebut adalah . Membiarkan .

Jelas, adalah solusi untuk persamaan. Pada interval. Fungsinya negatif. Oleh karena itu, akar persamaan lainnya harus dicari hanya pada interval x dan .

Dengan bantuan mikrokalkulator, pertama-tama kita menemukan nilai perkiraan akar persamaan. Untuk melakukan ini, kami mengkompilasi tabel nilai fungsi pada interval dan ; yaitu, pada interval dan .

0	0	202,5	0,85355342
3	-0,00080306	207	0,6893642
6	-0,00119426	210	0,57635189
9	-0,00261932	213	0,4614465
12	-0,00448897	216	0,34549155
15	-0,00667995	219	0,22934931
18	-0,00903692	222	0,1138931
21	-0,01137519	225	0,00000002
24	-0,01312438	228	-0,11145712
27	-0,01512438	231	-0,21961736
30	-0,01604446	234	-0,32363903
33	-0,01597149	237	-0,42270819
36	-0,01462203	240	-0,5160445
39	-0,01170562	243	-0,60290965
42	-0,00692866	246	-0,65261345
45	0,00000002	249	-0,75452006
48	0,00936458	252	-0,81805397
51	0,02143757	255	-0,87270535
54	0,03647455	258	-0,91803444
57	0,0547098	261	-0,95367586
60	0,07635185	264	-0,97934187
63	0,10157893	267	-0,99482505
66	0,1305352	270	-1
67,5	0,14644661

Hipotesis berikut mudah dilihat dari tabel: akar persamaan milik segmen adalah angka: ; ; . Verifikasi langsung mengkonfirmasi hipotesis ini.

Menjawab. ; ; .

Menyelesaikan pertidaksamaan trigonometri menggunakan lingkaran satuan

Saat memecahkan pertidaksamaan trigonometri bentuk , di mana merupakan salah satu fungsi trigonometri, akan lebih mudah untuk menggunakan lingkaran trigonometri untuk menyajikan solusi pertidaksamaan dengan paling jelas dan menuliskan jawabannya. Metode utama untuk menyelesaikan pertidaksamaan trigonometri adalah dengan mereduksinya menjadi pertidaksamaan jenis yang paling sederhana . Mari kita lihat contoh bagaimana memecahkan ketidaksetaraan tersebut.

Contoh Memecahkan ketidaksetaraan.

Larutan. Mari kita menggambar lingkaran trigonometri dan menandai di atasnya titik-titik yang ordinatnya lebih besar dari .

Untuk solusi pertidaksamaan ini adalah . Juga jelas bahwa jika beberapa nomor berbeda dari beberapa nomor dari interval yang ditunjukkan oleh , maka itu juga tidak kurang dari . Oleh karena itu, ke ujung segmen solusi yang ditemukan, Anda hanya perlu menambahkan . Akhirnya, kami mendapatkan bahwa solusi dari ketidaksetaraan asli adalah semua .

Menjawab. .

Untuk menyelesaikan pertidaksamaan dengan tangen dan kotangen, konsep garis singgung dan kotangen berguna. Ini adalah garis dan, masing-masing (pada gambar (1) dan (2)), menyentuh lingkaran trigonometri.

Sangat mudah untuk melihat bahwa jika Anda membangun sebuah sinar dengan asal di titik asal, membuat sudut dengan arah positif dari sumbu absis, maka panjang segmen dari titik ke titik perpotongan sinar ini dengan garis garis singgung tepat sama dengan garis singgung sudut yang dibuat sinar ini dengan sumbu absis. Pengamatan serupa berlaku untuk kotangen.

Contoh Memecahkan ketidaksetaraan.

Larutan. Dinotasikan , maka pertidaksamaan akan berbentuk yang paling sederhana: . Pertimbangkan interval dengan panjang yang sama dengan periode positif terkecil (LPP) dari garis singgung. Pada segmen ini, dengan menggunakan garis singgung, kami menetapkan bahwa . Kami sekarang mengingat apa yang perlu ditambahkan, karena RPE fungsi . Jadi, . Kembali ke variabel , kita mendapatkan itu .

Menjawab. .

Lebih mudah untuk menyelesaikan pertidaksamaan dengan fungsi trigonometri terbalik menggunakan grafik fungsi trigonometri terbalik. Mari kita tunjukkan bagaimana ini dilakukan dengan sebuah contoh.

Memecahkan pertidaksamaan trigonometri dengan metode grafis

Perhatikan bahwa jika --- fungsi periodik, maka untuk menyelesaikan pertidaksamaan tersebut, perlu dicari penyelesaiannya pada ruas yang panjangnya sama dengan periode fungsi . Semua solusi dari pertidaksamaan asli akan terdiri dari nilai-nilai yang ditemukan, serta semua yang berbeda dari yang ditemukan oleh sejumlah bilangan bulat periode fungsi.

Perhatikan solusi pertidaksamaan ().

Karena , maka pertidaksamaan tidak memiliki solusi untuk . Jika , maka himpunan penyelesaian pertidaksamaan --- banyak semua bilangan real.

Membiarkan . Fungsi sinus memiliki periode positif terkecil, sehingga pertidaksamaan dapat diselesaikan terlebih dahulu pada segmen yang panjangnya , misalnya pada segmen. Kami membangun grafik fungsi dan (). diberikan oleh ketidaksetaraan bentuk: dan, dari mana,

Dalam makalah ini, metode untuk memecahkan persamaan dan pertidaksamaan trigonometri, baik yang paling sederhana maupun tingkat Olimpiade, dipertimbangkan. Metode utama untuk memecahkan persamaan dan pertidaksamaan trigonometri dipertimbangkan, baik spesifik --- karakteristik hanya untuk persamaan dan pertidaksamaan trigonometri --- dan metode fungsional umum untuk menyelesaikan persamaan dan pertidaksamaan, seperti yang diterapkan pada persamaan trigonometri.

Tesis ini memberikan informasi teoritis dasar: definisi dan sifat-sifat trigonometri dan fungsi trigonometri terbalik; ekspresi fungsi trigonometri dalam hal fungsi trigonometri lainnya, yang sangat penting untuk mengubah ekspresi trigonometri, terutama yang mengandung fungsi trigonometri terbalik; selain rumus trigonometri dasar, yang sudah dikenal dari kursus sekolah, diberikan rumus yang menyederhanakan ekspresi yang mengandung fungsi trigonometri terbalik. Solusi persamaan trigonometri dasar, metode pemfaktoran, metode pengurangan persamaan trigonometri menjadi persamaan aljabar dipertimbangkan. Mengingat fakta bahwa solusi persamaan trigonometri dapat ditulis dalam beberapa cara, dan bentuk solusi ini tidak memungkinkan seseorang untuk segera menentukan apakah solusi ini sama atau berbeda, skema umum untuk menyelesaikan persamaan trigonometri dipertimbangkan dan transformasi kelompok solusi umum persamaan trigonometri dipertimbangkan secara rinci. Metode untuk memecahkan pertidaksamaan trigonometri dasar, baik pada lingkaran satuan dan dengan metode grafis, dipertimbangkan secara rinci. Proses penyelesaian pertidaksamaan trigonometri non-dasar melalui pertidaksamaan dasar dan metode interval yang sudah dikenal oleh anak sekolah dijelaskan. Solusi dari tugas-tugas khas untuk pemilihan akar diberikan. Informasi teoretis yang diperlukan untuk pemilihan akar diberikan: partisi himpunan bilangan bulat menjadi himpunan bagian yang tidak berpotongan, solusi persamaan dalam bilangan bulat (diophantine).

Hasil karya skripsi ini dapat digunakan sebagai bahan pendidikan dalam penyusunan makalah dan skripsi, dalam penyusunan pilihan untuk anak sekolah, dan karya tersebut juga dapat digunakan dalam mempersiapkan siswa untuk ujian masuk dan ujian terpusat.

Vygodsky Ya.Ya., Buku Pegangan matematika dasar. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.

Igudisman O., Matematika pada ujian lisan / Igudisman O. --- M.: Iris press, Rolf, 2001.

Azarov A.I., persamaan / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994.

Litvinenko V.N., Lokakarya matematika dasar / Litvinenko V.N. --- M .: Pendidikan, 1991.

Sharygin I.F., Kursus opsional dalam matematika: pemecahan masalah / Sharygin I.F., Golubev V.I. --- M.: Pencerahan, 1991.

Bardushkin V., Persamaan trigonometri. Pemilihan akar / V. Bardushkin, A. Prokofiev.// Matematika, No. 12, 2005 hal. 23--27.

Vasilevsky A.B., Tugas untuk pekerjaan ekstrakurikuler dalam matematika / Vasilevsky A.B. --- Mn.: Asveta Rakyat. 1988. --- 176s.

Sapunov P. I., Transformasi dan penyatuan kelompok solusi umum persamaan trigonometri / Sapunov P. I. // Pendidikan matematika, edisi No. 3, 1935.

Borodin P., Trigonometri. Materi ujian masuk di Universitas Negeri Moskow [teks] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Matematika No. 1, 2005 hal. 36--48.

Samusenko A.V., Matematika: Kesalahan khas pelamar: Manual referensi / Samusenko A.V., Kazachenok V.V. --- Minsk: Higher School, 1991.

Azarov A.I., Metode fungsional dan grafis untuk memecahkan masalah pemeriksaan / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.

DEFINISI

Pertidaksamaan trigonometri adalah pertidaksamaan yang memuat variabel di bawah tanda fungsi trigonometri.

Menyelesaikan pertidaksamaan trigonometri

Penyelesaian pertidaksamaan trigonometri sering kali diturunkan ke penyelesaian pertidaksamaan trigonometri paling sederhana dalam bentuk: \(\ \sin x a \), \(\ \cos x > a \), \(\ \namaoperator(tg) x > a \ ), \(\ \ nama operator(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \namaoperator(tg) x \ leq a \), \ (\ \nama operator(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \namaoperator(tg ) x \geq a \ ), \(\ \namaoperator(tg) x \geq a \)

Pertidaksamaan trigonometri paling sederhana diselesaikan secara grafis atau menggunakan lingkaran trigonometri satuan.

Menurut definisi, sinus sudut \(\ \alpha \) adalah ordinat titik \(\ P_(\alpha)(x, y) \) dari lingkaran satuan (Gbr. 1), dan kosinusnya adalah absis titik ini. Fakta ini digunakan dalam menyelesaikan pertidaksamaan trigonometri paling sederhana dengan cosinus dan sinus menggunakan lingkaran satuan.

Contoh penyelesaian pertidaksamaan trigonometri

Latihan

Selesaikan pertidaksamaan \(\ \sin x \leq \frac(\sqrt(3))(2) \)

Solusi

Karena \(\ \left|\frac(\sqrt(3))(2)\right| , pertidaksamaan ini memiliki solusi dan dapat diselesaikan dengan dua cara

Cara pertama. Mari selesaikan pertidaksamaan ini secara grafis. Untuk melakukan ini, kita membangun dalam sistem koordinat yang sama grafik sinus \(\ y=\sin x \) (Gbr. 2) dan garis lurus \(\ y=\frac(\sqrt(3))( 2) \)

Mari kita pilih interval di mana sinusoid berada di bawah grafik garis lurus \(\ y=\frac(\sqrt(3))(2) \) . Cari absis \(\ x_(1) \) dan \(\ x_(2) \) dari titik potong grafik berikut: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3 ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Kami mendapatkan interval \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) tetapi karena fungsi \(\ y=\sin x \) periodik dan memiliki periode \(\ 2 \pi \) , maka jawabannya adalah gabungan interval: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\kanan] \), \(\ k \di Z \)

Cara kedua. Bangun lingkaran satuan dan garis \(\ y=\frac(\sqrt(3))(2) \) , tunjukkan titik potongnya \(\ P_(x_(1)) \) dan \(\ P_(x_ (2)) \) (Gbr. 3). Solusi dari pertidaksamaan awal adalah himpunan titik-titik ordinat yang lebih kecil dari \(\ \frac(\sqrt(3))(2) \) . Cari nilai \(\ \boldsymbol(I)_(1) \) dan \(\ \boldsymbol(I)_(2) \) dengan berlawanan arah jarum jam, \(\ x_(1) Gbr. 3

\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Dengan mempertimbangkan periodisitas fungsi sinus, akhirnya diperoleh interval \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\kanan] \), \(\k\di Z\)

Jawab\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\kanan] \), \(\ k \di Z\)

Latihan

Selesaikan pertidaksamaan \(\ \sin x>2 \)

Larutan

Sinus adalah fungsi terbatas: \(\ |\sin x| \leq 1 \) , dan ruas kanan pertidaksamaan ini lebih besar dari satu, jadi tidak ada solusi.

Jawaban: Tidak ada solusi.

Latihan

Selesaikan pertidaksamaan \(\ \cos x>\frac(1)(2) \)

Larutan

Pertidaksamaan ini dapat diselesaikan dengan dua cara: secara grafik dan menggunakan lingkaran satuan. Mari kita pertimbangkan masing-masing metode.

Cara pertama. Mari kita gambarkan dalam satu sistem koordinat fungsi yang menggambarkan bagian kiri dan kanan pertidaksamaan, yaitu \(\ y=\cos x \) dan \(\ y=\frac(1)(2) \) . Mari kita pilih interval di mana grafik fungsi kosinus \(\ y=\cos x \) terletak di atas grafik garis lurus \(\ y=\frac(1)(2) \) (Gbr. 4 ).

Cari absis dari titik \(\ \boldsymbol(x)_(1) \) dan \(\ x_(2) \) - titik potong grafik fungsi \(\ y=\cos x \ ) dan \(\ y=\frac (1)(2) \) , yang merupakan ujung dari salah satu interval di mana ketidaksamaan yang ditunjukkan berlaku. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

Mengingat kosinus adalah fungsi periodik, dengan periode \(\ 2 \pi \) , jawabannya adalah nilai \(\ x \) dari interval \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\kanan) \), \(\ k \in Z \)

Cara kedua. Mari kita buat lingkaran satuan dan garis lurus \(\ x=\frac(1)(2) \) (karena sumbu x berhubungan dengan kosinus pada lingkaran satuan). Misalkan \(\ P_(x_(1)) \) dan \(\ P_(x_(2)) \) (Gbr. 5) adalah titik potong garis dan lingkaran satuan. Solusi persamaan awal adalah himpunan titik-titik absis yang lebih kecil dari \(\ \frac(1)(2) \) . Cari nilai \(\ x_(1) \) dan \(\ 2 \) , membuat tur berlawanan arah jarum jam sehingga \(\ x_(1) Dengan mempertimbangkan periodisitas kosinus, kami akhirnya mendapatkan interval \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)

Jawaban: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \di Z \)

Latihan

Selesaikan pertidaksamaan \(\ \namaoperator(ctg) x \leq-\frac(\sqrt(3))(3) \)

Larutan

Mari kita plot grafik fungsi \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) dalam satu sistem koordinat

Mari kita pilih interval di mana grafik fungsi \(\ y=\namaoperator(ctg) x \) tidak lebih tinggi dari grafik garis lurus \(\ y=-\frac(\sqrt(3))(3 ) \) (Gbr. 6) .

Cari absis titik \(\ x_(0) \) , yang merupakan akhir dari salah satu interval di mana pertidaksamaan \(\ x_(0)=\namaoperator(arcctg)\left(-\frac(\ kuadrat(3))( 3)\kanan)=\pi-\namaoperator(arcctg)\kiri(\frac(\sqrt(3))(3)\kanan)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)

Ujung lain dari celah ini adalah titik \(\ \pi \) , dan fungsi \(\ y=\operatorname(ctg) x \) tidak terdefinisi pada titik ini. Jadi, salah satu solusi dari pertidaksamaan ini adalah interval \(\ \frac(2 \pi)(3) \leq x

Jawaban: \(\ x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\kanan) \), \(\ k \in Z \)

Pertidaksamaan trigonometri dengan argumen kompleks

Pertidaksamaan trigonometri dengan argumen kompleks dapat direduksi menjadi pertidaksamaan trigonometri paling sederhana menggunakan substitusi. Setelah menyelesaikannya, substitusi terbalik dibuat dan yang tidak diketahui asli diekspresikan.

Latihan

Selesaikan pertidaksamaan \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

Larutan

Nyatakan kosinus pada ruas kanan pertidaksamaan ini: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

Kami melakukan penggantian \(\ t=2 x+100^(\circ) \) , setelah itu pertidaksamaan ini ditransformasikan ke pertidaksamaan paling sederhana \(\ \cos t \leq-\frac(1)(2) \ )

Mari kita selesaikan dengan menggunakan lingkaran satuan. Mari kita buat lingkaran satuan dan garis \(\ x=-\frac(1)(2) \) . Mari kita nyatakan \(\ P_(1) \) dan \(\ P_(2) \) sebagai titik potong garis dan lingkaran satuan (Gbr. 7).

Solusi dari pertidaksamaan awal adalah himpunan titik-titik absis, yang paling banyak \(\ -\frac(1)(2) \). Titik \(\ P_(1) \) sesuai dengan sudut \(\ 120^(\circ) \) , dan titik \(\ P_(2) \) . Jadi, dengan periode cosinus, kita mendapatkan \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ), \(\ n \di Z \)

Kami membuat substitusi terbalik \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)

Kami menyatakan \(\ \mathbf(x) \), untuk melakukan ini, pertama kurangi \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\di Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)

lalu, bagi dengan 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)

Jawab\(\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \), \ (\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \)

Pertidaksamaan trigonometri ganda

Latihan

Memecahkan pertidaksamaan trigonometri ganda \(\ \frac(1)(2)

Larutan

Mari kita perkenalkan penggantian \(\ t=\frac(x)(2) \) , maka pertidaksamaan asli akan berbentuk \(\ \frac(1)(2)

Mari kita selesaikan dengan menggunakan lingkaran satuan. Karena sumbu ordinat sesuai dengan sinus pada lingkaran satuan, kami memilih di atasnya himpunan ordinat yang lebih besar dari \(\ x=\frac(1)(2) \) dan kurang dari atau sama dengan \(\ \frac(\sqrt(2))(2 ) \) . Pada Gambar 8, titik-titik ini akan ditempatkan pada busur \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) dan \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Mari kita cari nilainya \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , membuat tur berlawanan arah jarum jam, dan \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)

Dengan demikian, kita memperoleh dua interval, yang, dengan mempertimbangkan periodisitas fungsi sinus, dapat ditulis sebagai berikut \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), untuk ini kita kalikan semua sisi dari kedua pertidaksamaan dengan 2, kita mendapatkan \(\ \frac (\pi)(3)+4 \pi k \leq x

Jawab\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\right] \cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\kanan) \), \(\ k \in Z \)

Dalam pelajaran praktis, kami akan mengulangi jenis tugas utama dari topik "Trigonometri", kami juga akan menganalisis masalah dengan peningkatan kompleksitas dan mempertimbangkan contoh penyelesaian berbagai ketidaksetaraan trigonometri dan sistemnya.

Pelajaran ini akan membantu Anda mempersiapkan salah satu jenis tugas B5, B7, C1 dan C3.

Mari kita mulai dengan mengulangi jenis tugas utama yang telah kita ulas dalam topik Trigonometri dan menyelesaikan beberapa tugas non-standar.

Tugas 1. Ubah sudut menjadi radian dan derajat: a) ; b) .

a) Gunakan rumus untuk mengubah derajat ke radian

Substitusikan nilai yang diberikan ke dalamnya.

b) Terapkan rumus untuk mengubah radian ke derajat

Ayo lakukan substitusi .

Menjawab. sebuah) ; b) .

Tugas #2. Hitung: a) ; b) .

a) Karena sudut jauh di luar meja, kami menguranginya dengan mengurangi periode sinus. Karena sudut diberikan dalam radian, maka periode akan dianggap sebagai .

b) Dalam hal ini, situasinya serupa. Karena sudut ditentukan dalam derajat, maka kita akan mempertimbangkan periode garis singgung sebagai .

Sudut yang dihasilkan, meskipun lebih kecil dari periode, lebih besar, yang berarti tidak lagi merujuk ke utama, tetapi ke bagian tabel yang diperpanjang. Agar tidak melatih memori kita sekali lagi dengan menghafal tabel nilai trigofungsi yang diperluas, kita kurangi lagi periode tangen:

Kami mengambil keuntungan dari keanehan fungsi tangen.

Menjawab. a) 1; b) .

Tugas #3. Menghitung , jika .

Kami membawa seluruh ekspresi ke garis singgung dengan membagi pembilang dan penyebut pecahan dengan . Pada saat yang sama, kita tidak boleh takut akan hal itu, karena dalam hal ini, nilai tangen tidak akan ada.

Tugas #4. Sederhanakan ekspresi.

Ekspresi yang ditentukan dikonversi menggunakan formula cast. Hanya saja mereka tidak biasa ditulis menggunakan derajat. Ekspresi pertama umumnya berupa angka. Sederhanakan semua fungsi trigo secara bergantian:

Karena , maka fungsi berubah menjadi kofungsi, yaitu. ke kotangen, dan sudut jatuh ke kuartal kedua, di mana tanda garis singgung awal adalah negatif.

Untuk alasan yang sama seperti pada ekspresi sebelumnya, fungsi berubah menjadi kofungsi, mis. ke kotangen, dan sudut jatuh ke kuartal pertama, di mana garis singgung awal memiliki tanda positif.

Mengganti semuanya menjadi ekspresi yang disederhanakan:

Tugas #5. Sederhanakan ekspresi.

Mari kita tulis garis singgung sudut ganda sesuai dengan rumus yang sesuai dan sederhanakan ekspresinya:

Identitas terakhir adalah salah satu formula pengganti universal untuk kosinus.

Tugas #6. Hitung.

Hal utama adalah tidak membuat kesalahan standar dan tidak memberikan jawaban yang ekspresinya sama dengan . Tidak mungkin untuk menggunakan properti utama dari garis singgung busur sementara ada faktor dalam bentuk dua di dekatnya. Untuk menghilangkannya, kami menulis ekspresi sesuai dengan rumus untuk garis singgung sudut ganda, sementara kami memperlakukannya sebagai argumen biasa.

Sekarang sudah dimungkinkan untuk menerapkan properti utama dari tangen busur, ingat bahwa tidak ada batasan pada hasil numeriknya.

Tugas #7. Memecahkan persamaan.

Ketika memecahkan persamaan pecahan yang sama dengan nol, selalu ditunjukkan bahwa pembilangnya adalah nol dan penyebutnya tidak, karena Anda tidak dapat membagi dengan nol.

Persamaan pertama adalah kasus khusus dari persamaan paling sederhana, yang diselesaikan menggunakan lingkaran trigonometri. Pikirkan tentang solusi ini sendiri. Pertidaksamaan kedua diselesaikan sebagai persamaan paling sederhana menggunakan rumus umum untuk akar-akar garis singgung, tetapi hanya dengan tanda tidak sama.

Seperti yang dapat kita lihat, satu keluarga akar mengecualikan keluarga akar lain yang persis sama yang tidak memenuhi persamaan. Itu. tidak ada akar.

Menjawab. Tidak ada akar.

Tugas #8. Memecahkan persamaan.

Segera perhatikan bahwa Anda dapat mengambil faktor umum dan melakukannya:

Persamaan telah direduksi menjadi salah satu bentuk standar, ketika produk dari beberapa faktor sama dengan nol. Kita sudah tahu bahwa dalam hal ini salah satunya sama dengan nol, atau yang lain, atau yang ketiga. Kami menulis ini sebagai satu set persamaan:

Dua persamaan pertama adalah kasus khusus dari yang paling sederhana, kami telah bertemu dengan persamaan serupa berkali-kali, jadi kami akan segera menunjukkan solusinya. Kami mengurangi persamaan ketiga menjadi satu fungsi menggunakan rumus sinus sudut ganda.

Mari selesaikan persamaan terakhir secara terpisah:

Persamaan ini tidak memiliki akar, karena nilai sinus tidak bisa melampaui .

Jadi, hanya dua keluarga akar pertama yang solusinya, mereka dapat digabungkan menjadi satu, yang mudah ditunjukkan pada lingkaran trigonometri:

Ini adalah keluarga dari semua bagian, yaitu.

Mari kita beralih ke penyelesaian pertidaksamaan trigonometri. Pertama, mari kita menganalisis pendekatan untuk memecahkan contoh tanpa menggunakan rumus solusi umum, tetapi dengan bantuan lingkaran trigonometri.

Tugas #9. Memecahkan ketidaksetaraan.

Gambarlah garis bantu pada lingkaran trigonometri yang sesuai dengan nilai sinus yang sama dengan , dan tunjukkan interval sudut yang memenuhi pertidaksamaan.

Sangat penting untuk memahami dengan tepat bagaimana menentukan interval sudut yang dihasilkan, mis. apa awalnya dan apa akhirnya. Awal celah akan menjadi sudut yang sesuai dengan titik yang akan kita masuki di awal celah jika kita bergerak berlawanan arah jarum jam. Dalam kasus kami, ini adalah titik yang ada di sebelah kiri, karena bergerak berlawanan arah jarum jam dan melewati titik yang tepat, sebaliknya, kami keluar dari interval sudut yang diperlukan. Oleh karena itu, titik yang tepat akan sesuai dengan ujung celah.

Sekarang kita perlu memahami nilai sudut awal dan akhir dari celah solusi kita untuk pertidaksamaan. Kesalahan tipikal adalah dengan segera menunjukkan bahwa titik kanan sesuai dengan sudut , kiri dan memberikan jawabannya. Ini tidak benar! Harap dicatat bahwa kami baru saja menunjukkan interval yang sesuai dengan bagian atas lingkaran, meskipun kami tertarik pada yang lebih rendah, dengan kata lain, kami telah mencampur awal dan akhir interval solusi yang kami butuhkan.

Agar interval dimulai di sudut titik kanan dan berakhir di sudut titik kiri, sudut yang ditentukan pertama harus kurang dari yang kedua. Untuk melakukan ini, kita harus mengukur sudut titik yang tepat dalam arah referensi negatif, yaitu. searah jarum jam dan itu akan sama dengan . Kemudian, mulai dari arah positif searah jarum jam, kita akan sampai ke titik kanan setelah titik kiri dan mendapatkan nilai sudutnya. Sekarang awal interval sudut kurang dari akhir , dan kita dapat menulis interval solusi tanpa memperhitungkan periode:

Mempertimbangkan bahwa interval seperti itu akan berulang dalam jumlah tak terbatas setelah sejumlah rotasi bilangan bulat, kami mendapatkan solusi umum, dengan mempertimbangkan periode sinus:

Kami menempatkan tanda kurung bulat karena ketidaksetaraan ketat, dan kami menusuk titik-titik pada lingkaran yang sesuai dengan ujung interval.

Bandingkan jawaban Anda dengan rumus untuk solusi umum yang kami berikan dalam kuliah.

Menjawab. .

Metode ini bagus untuk memahami dari mana rumus untuk solusi umum dari pertidaksamaan trigonal paling sederhana berasal. Selain itu, berguna bagi mereka yang terlalu malas untuk mempelajari semua rumus rumit ini. Namun, metodenya sendiri juga tidak mudah, pilih pendekatan solusi mana yang paling nyaman bagi Anda.

Untuk menyelesaikan pertidaksamaan trigonometri, Anda juga dapat menggunakan grafik fungsi di mana garis bantu dibangun, mirip dengan metode yang ditunjukkan menggunakan lingkaran satuan. Jika Anda tertarik, cobalah untuk memahami pendekatan solusi ini sendiri. Berikut ini, kita akan menggunakan rumus umum untuk menyelesaikan pertidaksamaan trigonometri paling sederhana.

Tugas #10. Memecahkan ketidaksetaraan.

Kami menggunakan rumus solusi umum, dengan mempertimbangkan bahwa ketidaksetaraan tidak ketat:

Kami mendapatkan dalam kasus kami:

Menjawab.

Tugas #11. Memecahkan ketidaksetaraan.

Kami menggunakan rumus solusi umum untuk ketidaksetaraan ketat yang sesuai:

Menjawab. .

Tugas # 12. Memecahkan ketidaksetaraan: a) ; b) .

Dalam ketidaksetaraan ini, seseorang tidak boleh terburu-buru menggunakan rumus untuk solusi umum atau lingkaran trigonometri, cukup dengan mengingat kisaran nilai sinus dan kosinus.

a) Karena , maka pertidaksamaan tersebut tidak berarti. Oleh karena itu, tidak ada solusi.

b) Karena sama, sinus dari setiap argumen selalu memenuhi ketidaksetaraan yang ditentukan dalam kondisi. Oleh karena itu, ketidaksetaraan dipenuhi oleh semua nilai nyata dari argumen .

Menjawab. a) tidak ada solusi; b) .

Tugas 13. Selesaikan pertidaksamaan .

Solusi persamaan trigonometri paling sederhana

Pertama, mari kita ingat rumus untuk menyelesaikan yang paling sederhana persamaan trigonometri.

1. $sinx=a$

1. $cosx=a$

1. $tgx=a$

1. $ctgx=a$

Penyelesaian pertidaksamaan trigonometri paling sederhana.

Untuk menyelesaikan pertidaksamaan trigonometri yang paling sederhana, pertama-tama kita harus menyelesaikan persamaan yang sesuai, dan kemudian, menggunakan persamaan trigonometri lingkaran, Temukan solusi pertidaksamaan. Pertimbangkan solusi dari pertidaksamaan trigonometri paling sederhana dengan contoh.

Contoh 1

$sinx\ge \frac(1)(2)$

Temukan solusi dari pertidaksamaan trigonometri $sinx=\frac(1)(2)$

\ \

Gambar 1. Solusi pertidaksamaan $sinx\ge \frac(1)(2)$.

Karena pertidaksamaan memiliki tanda “lebih besar dari atau sama dengan”, penyelesaiannya terletak pada busur atas lingkaran (terhadap penyelesaian persamaan).

Jawaban: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.

Contoh 2

Temukan solusi dari pertidaksamaan trigonometri $cosx=\frac(\sqrt(3))(2)$

\ \

Perhatikan penyelesaian pada lingkaran trigonometri

Karena pertidaksamaan memiliki tanda "kurang dari", solusinya terletak pada busur lingkaran yang terletak di sebelah kiri (terhadap solusi persamaan).

Jawaban: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.

Contoh 3

$tgx\le \frac(\sqrt(3))(3)$

Temukan solusi dari pertidaksamaan trigonometri $tgx=\frac(\sqrt(3))(3)$

\ \

Di sini kita juga membutuhkan domain definisi. Seperti yang kita ingat fungsi tangen $x\ne \frac(\pi )(2)+\pi n,n\in Z$

Perhatikan penyelesaian pada lingkaran trigonometri

Gambar 3. Solusi pertidaksamaan $tgx\le \frac(\sqrt(3))(3)$.

Karena pertidaksamaan memiliki tanda “kurang dari atau sama dengan”, penyelesaiannya terletak pada busur lingkaran yang ditandai dengan warna biru pada Gambar 3.

Jawaban: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\kanan.\kiri.\frac(7\pi )(6)+2\pi n\kanan]$

Contoh 4

Temukan solusi dari pertidaksamaan trigonometri $ctgx=\sqrt(3)$

\ \

Di sini kita juga membutuhkan domain definisi. Seperti yang kita ingat, fungsi tangen $x\ne \pi n,n\in Z$

Perhatikan penyelesaian pada lingkaran trigonometri

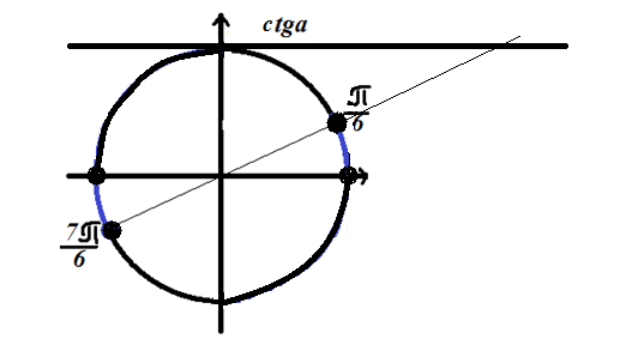
Gambar 4. Solusi pertidaksamaan $ctgx\le \sqrt(3)$.

Karena pertidaksamaan memiliki tanda “lebih besar dari”, penyelesaiannya terletak pada busur lingkaran yang ditandai dengan warna biru pada Gambar 4.

Jawaban: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\kanan)$