Contoh asimtot horizontal. Temukan asimtot grafik fungsi
- Konsep asimtot
Salah satu langkah penting dalam menyusun grafik fungsi adalah pencarian asimtot. Kami bertemu dengan asimtot lebih dari sekali: saat memplot fungsi , y=tgx, y=ctgx. Kami telah mendefinisikannya sebagai garis yang "cenderung" untuk grafik suatu fungsi tetapi tidak pernah berpotongan. Saatnya untuk memberikan definisi asimtot yang tepat.
Ada tiga jenis asimtot: vertikal, horizontal, dan miring. Dalam gambar, asimtot biasanya dilambangkan dengan garis putus-putus.
Pertimbangkan grafik fungsi yang diplot secara artifisial berikut (Gbr. 16.1), pada contoh di mana semua jenis asimtot terlihat jelas:
Kami memberikan definisi untuk setiap jenis asimtot:
1. Langsung x=a ditelepon asimtot vertikal berfungsi jika .
2. Langsung y=s ditelepon asimtot horisontal berfungsi jika .
3. Langsung y=kx+b ditelepon asimtot miring berfungsi jika .
Secara geometris, definisi asimtot miring berarti bahwa →∞ grafik suatu fungsi mendekati garis lurus yang menutup sembarang y=kx+b, yaitu mereka praktis sama. Perbedaan ekspresi yang hampir identik cenderung nol.
Perhatikan bahwa asimtot horizontal dan miring dianggap hanya dalam kondisi →∞. Kadang-kadang mereka dibedakan menjadi asimtot horizontal dan miring sebagai →+∞ dan →-∞.
- Algoritma Pencarian Asimtot
Algoritma berikut dapat digunakan untuk menemukan asimtot:
Mungkin ada satu asimtot vertikal, beberapa atau tidak sama sekali.
- Jika c adalah bilangan, maka y=s adalah asimtot horizontal;
- Jika c tak terhingga, maka tidak ada asimtot horizontal.
Jika suatu fungsi adalah rasio dari dua polinomial, maka jika fungsi tersebut memiliki asimtot horizontal, kami tidak akan mencari asimtot miring - asimtot tersebut tidak ada.
Pertimbangkan contoh menemukan asimtot suatu fungsi:
Contoh 16.1. Temukan asimtot kurva.
Larutan X-1≠0; X≠1.
Mari kita periksa apakah garisnya x= 1 asimtot vertikal. Untuk melakukan ini, kami menghitung batas fungsi pada titik tersebut x= 1: .
x= 1 - asimtot vertikal.
Dengan= .
Dengan= = . Karena Dengan=2 (bilangan), maka y=2 adalah asimtot horizontal.
Karena fungsinya adalah rasio polinomial, dengan adanya asimtot horizontal, kami menyatakan bahwa tidak ada asimtot miring.
x= 1 dan asimtot horizontal y=2. Untuk lebih jelasnya, grafik fungsi ini ditunjukkan pada Gambar. 16.2.
Contoh 16.2. Temukan asimtot kurva.
Larutan. 1. Temukan domain dari fungsi: X-2≠0; X≠2.
Mari kita periksa apakah garisnya x= 2 asimtot vertikal. Untuk melakukan ini, kami menghitung batas fungsi pada titik tersebut x= 2: .
Kami mendapatkannya, oleh karena itu, x= 2 - asimtot vertikal.
2. Untuk mencari asimtot horizontal, kita cari: Dengan= .
Karena ada ketidakpastian dalam batas, kami menggunakan aturan L'Hopital: Dengan= = . Karena Dengan tak terhingga, maka tidak ada asimtot horizontal.
3. Untuk mencari asimtot miring, kami menemukan:
Kami mendapat ketidakpastian bentuk , kami menggunakan aturan L'Hopital: = =1. B sesuai dengan rumus: .
b= = =
Mengerti b= 2. Lalu y=kx+b – asimtot miring. Dalam kasus kami, ini terlihat seperti: y=x+2.
|
pertanyaan kontrol:
Kuliah 17
Dalam kuliah ini, kami akan merangkum semua materi yang dipelajari sebelumnya. Tujuan akhir dari perjalanan panjang kami adalah untuk dapat menyelidiki fungsi yang diberikan secara analitis dan membangun grafiknya. Bagian penting dari penelitian kami adalah studi tentang fungsi untuk ekstrem, penentuan interval kemonotonan, kecembungan dan kecekungan grafik, pencarian titik belok, asimtot grafik fungsi.
Dengan mempertimbangkan semua aspek di atas, kami sajikan skema untuk mempelajari fungsi dan plotting .
1. Temukan domain dari fungsi tersebut.
2. Menyelidiki fungsi genap-ganjil:
jika , maka fungsinya genap (grafik bahkan fungsi simetris terhadap sumbu OU);
jika , maka fungsinya ganjil (grafik fungsi ganjil simetris terhadap asal);
Jika tidak, fungsinya bukan genap atau ganjil.
3. Selidiki fungsi periodisitas (di antara fungsi-fungsi yang kita pelajari, hanya fungsi trigonometri yang bisa periodik).
4. Temukan titik potong grafik fungsi dengan sumbu koordinat:
· Oh: pada=0 (kami menyelesaikan persamaan hanya jika kami dapat menggunakan metode yang kami ketahui);
· OU: X=0.
5. Temukan turunan pertama dari fungsi dan titik kritis dari jenis pertama.
6. Temukan interval monoton dan ekstrem dari fungsi tersebut.
7. Temukan turunan kedua dari fungsi dan titik kritis dari jenis kedua.
8. Temukan interval cembung-cekung dari grafik fungsi dan titik belok.
9. Temukan asimtot dari grafik fungsi tersebut.
10. Grafik fungsinya. Saat membangun, pertimbangkan kasus kemungkinan lokasi grafis dekat asimtot :
11. Jika perlu, pilih titik kontrol untuk konstruksi yang lebih akurat.
Pertimbangkan skema untuk mempelajari suatu fungsi dan memplot grafiknya menggunakan contoh spesifik:
Contoh 17.1. Plot fungsinya.
Larutan. 1. Fungsi ini didefinisikan pada seluruh garis bilangan kecuali untuk X=3, karena pada titik ini penyebutnya menjadi nol.
2. Untuk menentukan kegenapan dan keganjilan fungsi, kita menemukan:
Kita lihat bahwa dan , oleh karena itu, fungsinya bukan genap atau ganjil.
3. Fungsinya non-periodik.
4. Temukan titik potong dengan sumbu koordinat. Untuk mencari titik potong dengan sumbu Oh menerima pada=0. Kami mendapatkan persamaan: . Jadi, titik (0; 0) merupakan titik potong dengan sumbu koordinat.
5. Temukan turunan dari fungsi sesuai dengan aturan pembagian pecahan: = = = = .
Untuk mencari titik kritis, kita mencari titik di mana turunan fungsinya sama dengan 0 atau tidak ada.
Jika =0, maka, . Produknya kemudian 0 ketika setidaknya salah satu faktornya adalah 0: atau .
X-3) 2 sama dengan 0, mis. tidak ada di X=3.
Jadi, fungsi tersebut memiliki tiga titik kritis jenis pertama: ; ; .
6. Aktif sumbu numerik kami menandai titik kritis dari jenis pertama, dan menandai titik tersebut dengan titik tertusuk, karena itu tidak mendefinisikan fungsi.
Susunlah tanda turunan = pada setiap interval:
|
|
Pada interval dimana , fungsi aslinya meningkat (at (-∞;0] ), dimana - menurun (at ).
Dot X=0 adalah titik maksimum dari fungsi. Untuk menemukan fungsi maksimum, mari kita cari nilai fungsi di titik 0: .
Dot X=6 adalah titik minimum dari fungsi. Untuk mencari minimum fungsi, mari kita cari nilai fungsi di poin 6: .
Hasil penelitian dapat dimasukkan dalam tabel. Jumlah baris dalam tabel adalah tetap dan sama dengan empat, dan jumlah kolom tergantung pada fungsi yang dipelajari. Dalam sel baris pertama, interval tempat titik kritis membagi domain definisi fungsi dimasukkan secara berurutan, termasuk titik kritis itu sendiri. Untuk menghindari kesalahan saat membuat titik yang tidak termasuk dalam area definisi, dimungkinkan untuk tidak memasukkannya ke dalam tabel.
Baris kedua tabel berisi tanda turunan pada setiap interval yang ditinjau dan nilai turunan pada titik kritis. Sesuai dengan tanda turunan fungsi, interval naik, turun, dan ekstrem fungsi ditandai pada baris ketiga.
Baris terakhir digunakan untuk menunjukkan fungsi maksimum dan minimum.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| kesimpulan | maks | min |
7. Temukan turunan kedua dari fungsi sebagai turunan dari turunan pertama: = =
Keluarkan di pembilang X-3 di luar tanda kurung dan lakukan pengurangan:
Kami hadir dalam pembilang seperti istilah: .
Mari kita cari titik kritis jenis kedua: titik di mana turunan kedua dari fungsi sama dengan nol atau tidak ada.
0 jika =0. Pecahan ini tidak boleh sama dengan nol, oleh karena itu, tidak ada titik di mana turunan kedua dari fungsi tersebut sama dengan nol.
Tidak ada jika penyebut ( X-3) 3 adalah 0, mis. tidak ada di X=3. :Oh , OU, asal, satuan ukuran untuk setiap sumbu.
Sebelum memplot fungsi, Anda perlu:
gambar asimtot dengan garis putus-putus;
tandai titik-titik perpotongan dengan sumbu koordinat;
|
· Dengan menggunakan data yang diperoleh pada interval naik, turun, cembung dan cekung, buatlah grafik fungsi tersebut. Cabang grafik harus "cenderung" ke asimtot, tetapi tidak melewatinya.
Periksa apakah grafik fungsi sesuai dengan penelitian: jika fungsinya genap atau ganjil, maka apakah kesimetriannya diamati; apakah secara teoritis ditemukan interval kenaikan dan penurunan, konveksitas dan cekungan, titik belok.
11. Untuk konstruksi yang lebih presisi, Anda dapat memilih beberapa titik kontrol. Sebagai contoh, mari kita cari nilai fungsi pada titik -2 dan 7:
Kami menyesuaikan grafik dengan mempertimbangkan titik kontrol.
pertanyaan kontrol:
- Apa algoritma untuk memplot grafik fungsi?
- Bisakah suatu fungsi memiliki ekstrem pada titik-titik yang tidak termasuk dalam domain definisi?
BAB 3. 3. KALKULU INTEGRAL FUNGSI
Asimtot grafik fungsi y \u003d f (x) disebut garis yang memiliki sifat jarak dari titik (x, f (x)) ke garis ini cenderung nol dengan penghapusan titik grafik yang tidak terbatas dari titik asal.
Gambar 3.10. contoh grafis diberikan vertikal, horisontal Dan miring asimtot.
Menemukan asimtot grafik didasarkan pada tiga teorema berikut.
Teorema asimtot vertikal. Biarkan fungsi y \u003d f (x) didefinisikan di beberapa lingkungan titik x 0 (mungkin mengecualikan titik ini sendiri) dan setidaknya salah satu dari batas satu sisi fungsi sama dengan tak terhingga, mis. Maka garis x \u003d x 0 adalah asimtot vertikal dari grafik fungsi y \u003d f (x).
Jelas, garis x \u003d x 0 tidak dapat menjadi asimtot vertikal jika fungsinya kontinu di titik x 0, karena dalam kasus ini 
. Oleh karena itu, asimtot vertikal harus dicari di titik diskontinuitas suatu fungsi atau di ujung domainnya.
Teorema asimtot horizontal. Biarkan fungsi y \u003d f (x) didefinisikan untuk x yang cukup besar dan ada batas fungsi yang terbatas . Maka garis y = b adalah asimtot horizontal dari grafik fungsi tersebut.
Komentar. Jika hanya salah satu limit yang berhingga, maka fungsi tersebut masing-masing memiliki, sisi kiri atau sisi kanan asimtot horisontal.
Jika , fungsi dapat memiliki asimtot miring.
Teorema asimtot miring. Biarkan fungsi y = f(x) didefinisikan untuk x yang cukup besar dan ada batas hingga 
. Maka garis y = kx + b adalah asimtot miring dari grafik fungsi tersebut.
Tanpa bukti.
Asimtot miring, serta asimtot horizontal, dapat berupa tangan kanan atau tangan kiri jika dasar dari batas yang sesuai adalah tak terhingga dari tanda tertentu.
Studi tentang fungsi dan konstruksi grafiknya biasanya mencakup langkah-langkah berikut:
1. Temukan domain dari fungsi tersebut.
2. Menyelidiki fungsi genap-ganjil.
3. Temukan asimtot vertikal dengan memeriksa titik-titik diskontinuitas dan perilaku fungsi pada batas-batas domain definisi, jika berhingga.
4. Temukan asimtot horizontal atau miring dengan memeriksa perilaku fungsi di tak terhingga.
5. Temukan ekstrem dan interval kemonotonan fungsi.
6. Temukan interval konveksitas dari fungsi dan titik belok.
7. Temukan titik perpotongan dengan sumbu koordinat dan, mungkin, beberapa titik tambahan yang menyempurnakan grafik.
Diferensial fungsi
Dapat dibuktikan bahwa jika suatu fungsi memiliki limit yang sama dengan bilangan hingga untuk basis tertentu, maka fungsi tersebut dapat direpresentasikan sebagai jumlah dari bilangan tersebut dan nilai sangat kecil untuk basis yang sama (dan sebaliknya): .
Mari terapkan teorema ini ke fungsi yang dapat dibedakan: .
Jadi, kenaikan fungsi Dy terdiri dari dua suku: 1) linier terhadap Dx, yaitu f`(x)Dx; 2) non-linear terhadap Dx, yaitu a(Dx)Dx. Pada saat yang sama, sejak 
, suku kedua ini sangat kecil dari orde yang lebih tinggi dari Dx (karena Dx cenderung nol, ia cenderung nol bahkan lebih cepat).
Diferensial fungsi disebut bagian utama dari peningkatan fungsi, linier terhadap Dx, sama dengan produk turunan dan peningkatan variabel independen dy = f `(x)Dx.
Temukan diferensial dari fungsi y = x.
Karena dy = f `(x)Dx = x`Dx = Dx, maka dx = Dx, yaitu diferensial variabel independen sama dengan kenaikan variabel ini.
Oleh karena itu, rumus diferensial suatu fungsi dapat ditulis sebagai dy = f `(x)dх. Oleh karena itu, salah satu simbol turunannya adalah pecahan dy/dх.
pengertian geometris diferensial diilustrasikan
gambar 3.11. Ambil sembarang titik M(x, y) pada grafik fungsi y = f(x). Mari beri argumen x kenaikan Dx. Maka fungsi y = f(x) akan menerima kenaikan Dy = f(x + Dх) - f(x). Mari menggambar garis singgung grafik fungsi di titik M, yang membentuk sudut a dengan arah positif sumbu x, mis. f `(x) = tg a. Dari segitiga siku-siku MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.
Jadi, diferensial suatu fungsi adalah pertambahan ordinat garis singgung yang ditarik ke grafik fungsi tersebut pada titik tertentu ketika x ditambah dengan Dx.
Sifat-sifat diferensial pada dasarnya sama dengan sifat turunan:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2 .
Namun, ada sifat penting dari diferensial suatu fungsi yang tidak dimiliki turunannya - yaitu invarian bentuk diferensial.
Dari definisi diferensial untuk fungsi y = f(x), diferensialnya adalah dy = f`(x)dх. Jika fungsi y ini kompleks, mis. y = f(u), di mana u = j(x), lalu y = f dan f `(x) = f `(u)*u`. Maka dy = f`(u)*u`dx. Tapi untuk fungsinya
u = j(x) diferensial du = u`dx. Oleh karena itu dy = f `(u)*du.
Membandingkan persamaan dy = f `(x)dх dan dy = f `(u)*du, kami memastikan bahwa rumus diferensial tidak berubah jika alih-alih fungsi variabel independen x kami menganggap fungsi variabel dependen u. Properti diferensial ini disebut invarian (yaitu, invarian) dari bentuk (atau rumus) diferensial.
Namun, masih ada perbedaan dalam kedua rumus ini: pada rumus pertama, diferensial variabel independen sama dengan kenaikan variabel ini, yaitu. dx = Dx, dan yang kedua, diferensial dari fungsi du hanyalah bagian linier dari kenaikan fungsi ini Du, dan hanya untuk Dх du » Du kecil.
Juga akan ada tugas untuk solusi mandiri yang dapat Anda lihat jawabannya.
Konsep asimtot
Jika Anda pertama kali membuat asimtot kurva, maka dalam banyak kasus konstruksi grafik fungsi difasilitasi.
Nasib asimtot penuh dengan tragedi. Bayangkan bagaimana rasanya bergerak dalam garis lurus ke tujuan yang disayangi sepanjang hidup Anda, sedekat mungkin dengannya, tetapi tidak pernah mencapainya. Misalnya, berusaha menghubungkan jalan hidup Anda dengan jalan orang yang diinginkan, pada titik tertentu mendekatinya hampir secara dekat, tetapi bahkan tidak menyentuhnya. Atau berusaha untuk menghasilkan satu miliar, tetapi sebelum mencapai tujuan ini dan masuk ke Guinness Book of Records untuk kasusnya, dia kekurangan seperseratus sen. Dll. Begitu pula dengan asimtot: ia terus-menerus berusaha mencapai kurva grafik fungsi, mendekatinya pada jarak seminimal mungkin, tetapi tidak menyentuhnya.
Definisi 1. Asimtot disebut garis yang mendekati grafik fungsi sedekat yang diinginkan ketika variabel cenderung plus tak terhingga atau minus tak terhingga.
Definisi 2. Suatu garis lurus disebut asimtot dari grafik suatu fungsi jika jaraknya dari titik variabel M grafik fungsi hingga garis ini cenderung nol saat titik bergerak menjauh tanpa batas M dari asal koordinat sepanjang setiap cabang dari grafik fungsi.
Ada tiga jenis asimtot: vertikal, horizontal dan miring.
Asimtot vertikal
Hal pertama yang harus diketahui tentang asimtot vertikal: mereka sejajar dengan sumbu Oy .
Definisi. Lurus X = A adalah asimtot vertikal dari grafik fungsi jika titik X = A adalah titik puncak dari jenis kedua untuk fitur ini.
Ini mengikuti dari definisi bahwa garis X = A adalah asimtot vertikal dari grafik fungsi F(X) jika setidaknya salah satu kondisi berikut terpenuhi:
Pada saat yang sama, fungsinya F(X) mungkin tidak didefinisikan sama sekali, masing-masing, untuk X ≥ A Dan X ≤ A .
Komentar:
Contoh 1 Grafik Fungsi y= dalam X memiliki asimtot vertikal X= 0 (yaitu bertepatan dengan sumbu Oy) pada batas domain definisi, karena limit fungsi sebagai x cenderung nol di sebelah kanan sama dengan minus tak terhingga:
(gbr. di atas).
sendiri dan kemudian lihat solusinya
Contoh 2 Temukan asimtot dari grafik fungsi .
Contoh 3 Temukan asimtot grafik fungsi
asimtot horisontal
Hal pertama yang harus diketahui tentang asimtot horizontal: mereka sejajar dengan sumbu Sapi .
Jika (batas fungsi ketika argumen cenderung plus atau minus tak terhingga sama dengan beberapa nilai B), Itu y = B – asimtot horisontal bengkok y = F(X ) (kanan saat x cenderung plus tak hingga, kiri saat x cenderung minus tak terhingga, dan bersisi dua jika limit saat x cenderung plus atau minus tak hingga sama).
Contoh 5 Grafik Fungsi
pada A> 1 memiliki asimtot horizontal kiri y= 0 (yaitu bertepatan dengan sumbu Sapi), karena limit fungsi ketika "x" cenderung minus tak terhingga sama dengan nol:
Kurva tidak memiliki asimtot horizontal tegak lurus, karena limit fungsi sebagai x cenderung ditambah tak terhingga sama dengan tak terhingga:
Asimtot miring
Asimtot vertikal dan horizontal yang kami pertimbangkan di atas sejajar dengan sumbu koordinat, oleh karena itu, untuk membangunnya, kami hanya membutuhkan angka tertentu - titik pada sumbu absis atau ordinat yang dilalui asimtot. Lebih banyak dibutuhkan untuk asimtot miring - kemiringan k, yang menunjukkan sudut kemiringan garis lurus, dan titik potong B, yang menunjukkan berapa banyak garis di atas atau di bawah titik asal. Mereka yang tidak punya waktu untuk melupakan geometri analitik, dan darinya - persamaan garis lurus, akan melihat bahwa untuk asimtot miring yang mereka temukan persamaan kemiringan. Keberadaan asimtot miring ditentukan oleh teorema berikut, yang menjadi dasar ditemukannya koefisien yang baru saja disebutkan.
Dalil. Untuk membuat kurva y = F(X) memiliki asimtot y = kx + B , perlu dan cukup bahwa ada batas-batas yang terbatas k Dan B dari fungsi yang dipertimbangkan sebagai variabel cenderung X ke plus tak terhingga dan minus tak terhingga:
(1)
(2)
Angka-angka demikian ditemukan k Dan B dan adalah koefisien asimtot miring.
Dalam kasus pertama (ketika x cenderung ditambah tak terhingga), diperoleh asimtot miring kanan, dalam kasus kedua (ketika x cenderung minus tak terhingga), kiri. Asimtot miring kanan ditunjukkan pada Gambar. dari bawah.
Saat menemukan persamaan asimtot miring, perlu diperhitungkan kecenderungan x ke plus tak terhingga dan minus tak terhingga. Untuk beberapa fungsi, misalnya, untuk pecahan rasional, batas ini sama, tetapi untuk banyak fungsi batas ini berbeda, dan hanya satu yang dapat ada.
Ketika batas bertepatan dengan x cenderung plus tak terhingga dan minus tak terhingga, garis lurus y = kx + B adalah asimtot dua sisi dari kurva.
Jika setidaknya salah satu batas mendefinisikan asimtot y = kx + B , tidak ada, maka grafik fungsi tersebut tidak memiliki asimtot miring (tetapi mungkin memiliki asimtot vertikal).
Sangat mudah untuk melihat asimtot horizontal y = B adalah kasus khusus miring y = kx + B pada k = 0 .
Oleh karena itu, jika suatu kurva memiliki asimtot horizontal ke segala arah, maka tidak ada asimtot miring ke arah tersebut, dan sebaliknya.
Contoh 6 Temukan asimtot grafik fungsi
Larutan. Fungsi didefinisikan pada seluruh garis bilangan kecuali X= 0 , mis.
Oleh karena itu, pada titik puncaknya X= 0 kurva mungkin memiliki asimtot vertikal. Memang, batas fungsi sebagai x cenderung nol dari kiri ditambah tak terhingga:
Karena itu, X= 0 adalah asimtot vertikal dari grafik fungsi ini.
Grafik fungsi ini tidak memiliki asimtot horizontal, karena limit fungsi ketika x cenderung ditambah tak terhingga sama dengan ditambah tak terhingga:
Mari kita cari tahu keberadaan asimtot miring:
Mendapat batas yang terbatas k= 2 dan B= 0 . Lurus y = 2X adalah asimtot miring dua sisi dari grafik fungsi ini (gbr. di dalam contoh).
Contoh 7 Temukan asimtot grafik fungsi
Larutan. Fungsi memiliki satu break point X= −1 . Mari kita hitung limit satu sisi dan tentukan jenis diskontinuitas:
Kesimpulan: X= −1 adalah titik diskontinuitas jenis kedua, jadi garisnya X= −1 adalah asimtot vertikal dari grafik fungsi ini.
Mencari asimtot miring. Karena fungsi ini rasional pecahan, batas untuk dan untuk akan sama. Jadi, kami menemukan koefisien untuk mengganti garis lurus - asimtot miring ke dalam persamaan:
Mengganti koefisien yang ditemukan ke dalam persamaan garis lurus dengan kemiringan, kita mendapatkan persamaan asimtot miring:
y = −3X + 5 .
Pada gambar, grafik fungsi ditandai dengan warna merah anggur, dan asimtotnya berwarna hitam.
Contoh 8 Temukan asimtot grafik fungsi
Larutan. Karena fungsi ini kontinu, grafiknya tidak memiliki asimtot vertikal. Kami mencari asimtot miring:
.
Jadi, grafik fungsi ini memiliki asimtot y= 0 di dan tidak memiliki asimtot di .
Contoh 9 Temukan asimtot grafik fungsi
Larutan. Pertama, kami mencari asimtot vertikal. Untuk melakukan ini, kami menemukan domain dari fungsi tersebut. Fungsi ini didefinisikan ketika pertidaksamaan berlaku dan . tanda variabel X cocok dengan tandanya. Oleh karena itu, pertimbangkan ketidaksetaraan setara . Dari sini kita mendapatkan ruang lingkup fungsi: 
. Asimtot vertikal hanya dapat berada di batas domain fungsi. Tetapi X= 0 tidak dapat berupa asimtot vertikal, karena fungsinya didefinisikan untuk X = 0
.
Pertimbangkan batas kanan di (batas kiri tidak ada):
.
Dot X= 2 adalah titik diskontinuitas jenis kedua, jadi garisnya X= 2 - asimtot vertikal dari grafik fungsi ini.
Kami mencari asimtot miring:
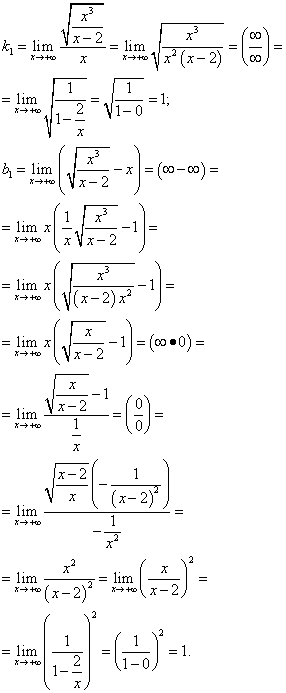
Jadi, y = X+ 1 - asimtot miring dari grafik fungsi ini di . Kami mencari asimtot miring untuk:
Jadi, y = −X − 1 - asimtot miring di .
Contoh 10 Temukan asimtot grafik fungsi
Larutan. Fungsi memiliki ruang lingkup 
. Karena asimtot vertikal dari grafik fungsi ini hanya dapat berada di batas daerah definisi, kita akan menemukan batas satu sisi dari fungsi di .
Solusinya dapat dengan mudah dipecah menjadi dua bagian:
1) Pertama kita periksa apakah ada asimtot vertikal. Penyebutnya hilang di, dan segera jelas bahwa pada titik ini fungsi mengalami diskontinuitas tak terhingga, dan garis lurus, diberikan oleh persamaan, adalah asimtot vertikal dari grafik fungsi. Tetapi sebelum menarik kesimpulan seperti itu, perlu untuk menemukan batasan satu sisi:
Saya mengingatkan Anda tentang teknik perhitungan, yang juga saya bahas di artikel Kontinuitas suatu fungsi. Titik istirahat. Dalam ekspresi di bawah tanda batas, alih-alih "x", kami menggantinya. Tidak ada yang menarik di pembilang:
Tetapi dalam penyebut, diperoleh bilangan negatif yang sangat kecil:
Ini menentukan nasib batas.
Batas kiri tidak terbatas, dan, pada prinsipnya, sudah mungkin untuk memberikan putusan tentang adanya asimtot vertikal. Tetapi batas satu sisi diperlukan tidak hanya untuk ini - mereka MEMBANTU ANDA MEMAHAMI BAGAIMANA grafik fungsi berada dan membangunnya dengan BENAR. Oleh karena itu, kita juga harus menghitung limit kanan:
Kesimpulan: limit satu sisi tak hingga, artinya garis lurus tersebut merupakan asimtot vertikal dari grafik fungsi di.
Batas pertama terbatas, artinya perlu "melanjutkan percakapan" dan menemukan batas kedua:
Batas kedua juga terbatas.
Jadi asimtot kita adalah:
Kesimpulan: garis lurus yang diberikan oleh persamaan adalah asimtot horizontal dari grafik fungsi di.
Untuk menemukan asimtot horizontal, Anda dapat menggunakan rumus yang disederhanakan:
Jika terdapat limit hingga, maka garis tersebut merupakan asimtot horizontal dari grafik fungsi di.
Sangat mudah untuk melihat bahwa pembilang dan penyebut fungsi memiliki urutan pertumbuhan yang sama, yang berarti batas yang diinginkan akan terbatas:
Sesuai dengan kondisinya, tidak perlu menyelesaikan gambarnya, tetapi jika kajian fungsinya berjalan lancar, maka kita langsung membuat sketsa pada drafnya:
Berdasarkan tiga batasan yang ditemukan, cobalah mencari tahu sendiri bagaimana grafik fungsi dapat ditemukan. Cukup sulit? Temukan 5-6-7-8 poin dan tandai pada gambar. Namun, grafik fungsi ini dibangun menggunakan transformasi grafik fungsi dasar, dan pembaca yang telah mempelajari Contoh 21 artikel ini dengan cermat akan dengan mudah menebak kurva seperti apa itu.
Ini adalah contoh do-it-yourself. Prosesnya, saya ingatkan, dengan mudah dibagi menjadi dua titik - asimtot vertikal dan asimtot miring. Dalam larutan sampel, asimtot horizontal ditemukan menggunakan skema yang disederhanakan.
Dalam praktiknya, fungsi pecahan-rasional paling sering ditemui, dan setelah pelatihan tentang hiperbola, kami akan memperumit tugas:
Temukan asimtot grafik fungsi
Solusi: Satu, dua dan selesai:
1) Asimtot vertikal berada pada titik diskontinuitas tak terhingga, jadi kita perlu memeriksa apakah penyebutnya hilang. Mari kita selesaikan persamaan kuadrat:
Diskriminan adalah positif, sehingga persamaan tersebut memiliki dua akar real dan ada banyak usaha yang ditambahkan
Untuk lebih lanjut menemukan batas satu sisi trinomial persegi Lebih mudah untuk memfaktorkan:
(untuk notasi ringkas, "minus" diperkenalkan di braket pertama). Untuk jaring pengaman, kami akan melakukan pemeriksaan, secara mental atau draf, membuka tanda kurung.
Mari tulis ulang fungsi dalam formulir
Temukan batas satu sisi pada suatu titik:
batas fungsi grafik asimtot
Dan pada intinya:
Jadi, garis lurus adalah asimtot vertikal dari grafik fungsi yang ditinjau.
2) Jika Anda melihat fungsinya, cukup jelas bahwa limitnya akan berhingga dan kita memiliki asimtot horizontal. Mari kita tunjukkan secara singkat:
Jadi, garis lurus (absis) adalah asimtot horizontal dari grafik fungsi ini.
Batas dan asimtot yang ditemukan memberikan banyak informasi tentang grafik fungsi. Coba bayangkan gambar itu secara mental, dengan mempertimbangkan fakta-fakta berikut:
Buat sketsa versi grafik Anda pada draf.
Tentu saja, batas yang ditemukan tidak secara jelas menentukan jenis grafik, dan Anda mungkin membuat kesalahan, tetapi latihan itu sendiri akan sangat membantu dalam mempelajari fungsi secara lengkap. Gambar yang benar ada di akhir pelajaran.
Temukan asimtot grafik fungsi
Temukan asimtot grafik fungsi
Ini adalah tugas untuk keputusan independen. Kedua grafik lagi memiliki asimtot horizontal, yang segera dideteksi oleh fitur-fitur berikut: dalam Contoh 4, penyebut bertambah dalam urutan besarnya lebih besar dari pembilang, dan dalam Contoh 5, pembilang dan penyebut memiliki urutan pertumbuhan yang sama. Dalam larutan sampel, fungsi pertama diselidiki untuk keberadaan asimtot miring secara penuh, dan yang kedua - melalui batas.
Asimtot horizontal, menurut kesan subjektif saya, terlihat lebih umum daripada asimtot yang "benar-benar miring". Kasus umum yang telah lama ditunggu:
Temukan asimtot grafik fungsi
Solusi: genre klasik:
- 1) Karena penyebutnya positif, fungsinya kontinu di seluruh garis bilangan, dan tidak ada asimtot vertikal. … Apakah itu baik? Bukan kata yang tepat - luar biasa! Item #1 ditutup.
- 2) Periksa keberadaan asimtot miring:
Batas kedua juga terbatas, oleh karena itu, grafik fungsi yang ditinjau memiliki asimtot miring:
Jadi, di , grafik fungsi tersebut sangat dekat dengan garis lurus.
Perhatikan bahwa ia memotong asimtot miringnya pada titik asal, dan titik persimpangan semacam itu cukup dapat diterima - penting bahwa "semuanya normal" pada tak terhingga (sebenarnya, diskusi tentang asimtot muncul di sana).
Temukan asimtot grafik fungsi
Solusi: tidak banyak yang perlu dikomentari, jadi saya akan membuat contoh perkiraan solusi akhir:
1) Asimtot vertikal. Mari jelajahi intinya.
Garis lurus adalah asimtot tegak bagi plot di.
2) Asimtot miring:
Garis lurus adalah asimtot miring untuk plot di.
Batas dan asimtot satu sisi yang ditemukan memungkinkan kita untuk berasumsi dengan pasti seperti apa grafik fungsi ini.
Temukan asimtot grafik fungsi
Ini adalah contoh untuk solusi independen, untuk kenyamanan menghitung beberapa batasan, Anda dapat membagi pembilang dengan suku penyebut dengan suku. Dan sekali lagi, setelah menganalisis hasilnya, coba gambar grafik fungsi ini.
Jelas, pemilik asimtot miring "nyata" adalah grafik dari fungsi fraksional-rasional yang tingkat pembilang tertingginya satu lebih besar dari tingkat tertinggi penyebutnya. Jika lebih - tidak akan ada asimtot miring (misalnya,).
Tetapi keajaiban lain juga terjadi dalam hidup.
