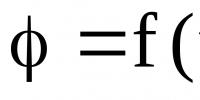Cos sin ღირებულება მეოთხედებში. როგორ დავიმახსოვროთ რიცხვითი წრის ძირითადი წერტილების კოსინუსების და სინუსების მნიშვნელობები

Გაკვეთილი 1

ნებისმიერი არგუმენტის ტრიგონომეტრიული ფუნქციები.

სინუსის, კოსინუსის, ტანგენსის და კოტანგენსის განმარტება და თვისებები.

კუთხის რადიანის ზომა.

ჩვენ აღვნიშნავთ A წერტილს Ox ღერძზე კოორდინატების საწყისიდან და ვხაზავთ წრეს ცენტრით O წერტილში. რადიუსი OA იქნება ე.წ. საწყისი რადიუსი.

კუთხე P (OM; OE) შეიძლება შეფასდეს, როგორც სხივის საწყისის გარშემო ბრუნვის შედეგი, საწყისი წერტილით O წერტილიდან OM - საწყისი პოზიციიდან OE - საბოლოო. ეს როტაცია შეიძლება იყოს საათის ისრის საწინააღმდეგოდ ან საათის ისრის მიმართულებით

ა) ან ნაწილობრივი შემობრუნებისთვის,

ბ) ან სრული რევოლუციების მთელი რიცხვით;

გ) ან სრული ბრუნვის მთელი რიცხვი და ნაწილობრივი ბრუნი.

საათის ისრის საწინააღმდეგოდ ორიენტირებული კუთხეების ზომები ითვლება დადებითად, ხოლო საათის ისრის მიმართულებით _ უარყოფითი

ჩვენ განვიხილავთ თანაბარ კუთხეებს ისეთ კუთხეებს, რომლებისთვისაც, როდესაც მათი საწყისი სხივები რაიმე ფორმით არის შერწყმული, საბოლოო სხივებიც გაერთიანებულია და მოძრაობა საწყისი სხივიდან ბოლოზე ერთი და იგივე მიმართულებით ხორციელდება იმავე რაოდენობისთვის. სრული და არასრული ბრუნვები O წერტილის გარშემო.

ნულოვანი კუთხეები ითვლება ტოლად.

კუთხის ზომების თვისებები:

არის კუთხე, რომლის ზომაა 1 - კუთხეების საზომი ერთეული. თანაბარი კუთხეებიაქვს თანაბარი ზომები. ორი კუთხის ჯამის ზომა უდრის კუთხეების ზომების ჯამს. ნულოვანი კუთხის ზომა არის ნული.

კუთხეების ყველაზე გავრცელებული ზომებია გრადუსები და რადიანები.

კუთხეების საზომი ერთეული გრადუსით არის ერთი გრადუსის სიდიდის კუთხე - გაფართოებული კუთხის 1/180. გეომეტრიის კურსიდან ცნობილია, რომ კუთხის ზომა გრადუსებში გამოიხატება რიცხვით 01.01.01. რაც შეეხება ბრუნვის კუთხეს, ის ნებისმიერნაირად შეიძლება იყოს გამოხატული გრადუსით ნამდვილი რიცხვი-∞-დან +∞-მდე.

როგორც საწყისზე ორიენტირებული წრე, ჩვენ ავიღებთ ერთეული რადიუსის წრეს, რომელიც აღვნიშნავთ მისი გადაკვეთის წერტილებს კოორდინატთა ღერძებთან. A (1;0), B (0;1), C (-1;0), D (0;-1). სხივი OA იქნება მიღებული, როგორც საწყისი კუთხე განხილული კუთხისთვის.

აბსცისა და ორდინატის კოორდინატთა ღერძი ერთმანეთის პერპენდიკულარულია და სიბრტყეს ყოფს ოთხ კოორდინატულ მეოთხედად: I, II, III, IV (იხ. სურათი).

იმის მიხედვით, თუ რომელ კოორდინატ კვარტალში იქნება OM რადიუსი, კუთხეα იქნება ამ მეოთხედის იგივე კუთხე.

ასე რომ, თუ 00< α <900 , то угол α - პირველი მეოთხედის კუთხე;

თუ 900< α <1800 , то угол α - მეორე მეოთხედის კუთხე;

თუ 1800 წ< α <2700 , то угол α - მესამე მეოთხედის კუთხე;

თუ 2700< α <3600 , то угол α - მეოთხე მეოთხედის კუთხე.

აშკარაა, რომ ბრუნთა მთელი რიცხვის დამატებისას კუთხეს მიიღება იმავე მეოთხედის კუთხე.

მაგალითად, კუთხე 4300 არის კუთხემე - ოჰ კვარტალი, 4300 \u003d 3600 + 700 \u003d 700 წლიდან;

კუთხე 9200 არის კუთხე III -მე კვარტალში, 9200 წლიდან = 3600 2 + 2000 = 2000 წ.

(ანუ მთელი რევოლუციების რაოდენობა შეიძლება იგნორირებული იყოს!)

კუთხეები 00, ± 900, ± 1800, ± 2700, ± 3600 - არ ეხება არცერთ მეოთხედს .

განვსაზღვროთ რომელი მეოთხედის კუთხეა კუთხეα თუ:

α \u003d 2830 (IV) α \u003d 1900 (III) α \u003d 1000 (II) α \u003d -200 (IV თ - უარყოფითი მიმართულება)

ახლა კი თავად:

α = 1790 α = 3250 α = 8000 α = -1200

გეომეტრიის დროს განისაზღვრა α კუთხის სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი

00 ≤ α ≤ 1800 . ჩვენ ახლა განვიხილავთ ამ განმარტებებს თვითნებური α კუთხისთვის.

font-size:12.0pt;line-height:115%">დაუშვით კუთხეα საწყისი რადიუსი OA გადადის OM რადიუსში.

კუთხის სინუსიα არის M წერტილის ორდინატის შეფარდება რადიუსის სიგრძესთან, ე.ი.

კუთხის კოსინუსიα არის M წერტილის აბსცისის შეფარდება რადიუსის სიგრძესთან, ე.ი.

კუთხის ტანგენტიα არის M წერტილის ორდინატის შეფარდება მის აბსცისასთან, ე.ი.

კუთხის კოტანგენსი α არის M წერტილის აბსცისის შეფარდება მის ორდინატთან, ე.ი.

განვიხილოთ ტრიგონომეტრიული ფუნქციების გამოთვლის მაგალითები ზოგიერთი კუთხის მნიშვნელობების ცხრილების გამოყენებით. ტირეები კეთდება მაშინ, როდესაც გამოხატვას აზრი არ აქვს.

α (გრადუსები)	00	300	450	600	900	1800	2700	3600
(მოხარული)	0					π		2π
sina
cosα
tgα
ctgα

მაგალითი №1. იპოვე sin300; cos450; tg600.

ამოხსნა: ა) იპოვეთ ცხრილის სვეტში sina და სტრიქონში 300, სვეტისა და ხაზის გადაკვეთაზე, ჩვენ ვპოულობთ მნიშვნელობასცოდვა 300 არის რიცხვი. ისინი ასე წერენ:ცოდვა 300 =

ბ) იპოვეთ ცხრილის სვეტში cosα და სტრიქონში 450, სვეტისა და ხაზის გადაკვეთაზე, ვპოულობთ მნიშვნელობას cos 450 არის რიცხვი. ისინი ასე წერენ: cos 450 =

გ) იპოვეთ ცხრილის სვეტშიტგა და სტრიქონში 600, სვეტისა და ხაზის გადაკვეთაზე, ვპოულობთ მნიშვნელობასტგ 600 არის რიცხვი EN-US style="font-size:12.0pt;line-height:115%"">tg600 =font-size:12.0pt;line-height:115%">მაგალითი #2

გამოთვალეთა) 2s os 600 + EN-US" style="font-size: 12.0pt;line-height:115%">cos300 = 2 შრიფტის ზომა:12.0pt;ხაზის სიმაღლე:115%"> ბ)3 tg 450 tg 600 = 3 1 https://pandia.ru/text/79/454/images/image017_6.gif" width="24" height="24 src=">

თავად გამოთვალეთ : ა) 5 sin 300 - ctg 450 ბ) 2 sin 300 + 6 cos 600 - 4 tg 450

გ ) 4ტგ 600 სინ 600 გ ) 2კოსინი 900 + 5 ტგ 1800

განვიხილოთ ტრიგონომეტრიული ფუნქციების ზოგიერთი თვისება.

მოდით გავარკვიოთ, რა ნიშნები აქვს სინუსს, კოსინუსს, ტანგენტს და კოტანგენტს თითოეულ კოორდინატთა მეოთხედში.

მოდით, OA რადიუსის შემობრუნებისას ტოლი იყოს R, α კუთხით , A წერტილი გადავიდა M წერტილში x და y კოორდინატებით. იმიტომ რომ(R = 1), შემდეგ ნიშანი დამოკიდებულია y-ის ნიშანზე.

I და II-ში მეოთხედი y>0 და in II და IV მეოთხედი - ზე<0.

Ნიშანი დამოკიდებულია x-ზე, რადგან, შემდეგ I და IV კუთხებისთვის - x > 0 და in

II და III კვარტალი x<0.

იმიტომ რომ ; , შემდეგ I და III კვარტალებში და აქვს "+" ნიშანი და II და IV მეოთხედებს აქვთ მინუს ნიშანი.

ბოლო გაკვეთილზე ჩვენ წარმატებით ავითვისეთ (ან გავიმეორეთ - როგორც ყველას მოსწონს) ყველა ტრიგონომეტრიის ძირითადი ცნებები. ის ტრიგონომეტრიული წრე , კუთხე წრეზე , ამ კუთხის სინუსი და კოსინუსი და ასევე აითვისა ტრიგონომეტრიული ფუნქციების ნიშნები მეოთხედებში . დეტალურად ისწავლა. თითებზე, შეიძლება ითქვას.

მაგრამ ეს ჯერ კიდევ არ არის საკმარისი. იმისათვის, რომ წარმატებით გამოვიყენოთ ყველა ეს მარტივი კონცეფცია პრაქტიკაში, ჩვენ გვჭირდება კიდევ ერთი სასარგებლო უნარი. კერძოდ, სწორი კუთხეებთან მუშაობა ტრიგონომეტრიაში. ტრიგონომეტრიაში ამ უნარის გარეშე - არაფერი. ყველაზე პრიმიტიულ მაგალითებშიც კი. რატომ? დიახ, რადგან კუთხე არის მთავარი მოქმედი ფიგურა ყველა ტრიგონომეტრიაში! არა არა ტრიგონომეტრიული ფუნქციები, არა სინუსი კოსინუსით, არა ტანგენსი კოტანგენსთან, კერძოდ თავად კუთხე. კუთხის გარეშე - ტრიგონომეტრიული ფუნქციების გარეშე, დიახ ...

როგორ ვიმუშაოთ კუთხეებით წრეზე? ამისათვის ირონიულად უნდა ვისწავლოთ ორი პუნქტი.

1) Როგორდათვლილია თუ არა წრეზე კუთხეები?

2) Რადათვლილია (იზომება)?

პირველ კითხვაზე პასუხი დღევანდელი გაკვეთილის თემაა. პირველ კითხვას დეტალურად განვიხილავთ აქ და ახლა. მეორე კითხვაზე პასუხი აქ არ იქნება. იმიტომ რომ საკმაოდ განვითარებულია. როგორც თავად მეორე კითხვა, ძალიან სრიალა, კი.) ჯერ დეტალებს არ შევეხები. ეს არის შემდეგი ცალკე გაკვეთილის თემა.

დავიწყოთ?

როგორ გამოითვლება კუთხეები წრეზე? დადებითი და უარყოფითი კუთხეები.

მათ, ვინც აბზაცის სათაურს წაიკითხავს, ​​შეიძლება უკვე თმა აიჩეჩა. Როგორ თუ?! უარყოფითი კუთხეები? შესაძლებელია კი ეს?

უარყოფითისკენ ნომრებიჩვენ უკვე შევეჩვიეთ. ჩვენ შეგვიძლია გამოვსახოთ ისინი რიცხვით ღერძზე: დადებითი ნულის მარჯვნივ, უარყოფითი ნულის მარცხნივ. დიახ, და ჩვენ პერიოდულად ვუყურებთ თერმომეტრს ფანჯრის გარეთ. მითუმეტეს ზამთარში, ყინვაში.) ტელეფონში ფული კი „მინუსშია“ (ე.ი. მოვალეობა) ხანდახან მიდიან. ეს ყველაფერი ნაცნობია.

მაგრამ რაც შეეხება კუთხეებს? გამოდის, რომ უარყოფითი კუთხეები მათემატიკაში ასევე მოხდეს!ეს ყველაფერი დამოკიდებულია იმაზე, თუ როგორ უნდა დაითვალოს ეს კუთხე ... არა, არა რიცხვით წრფეზე, არამედ რიცხვით წრეზე! ვგულისხმობ წრეში. წრე - აი, ეს არის რიცხვითი წრფის ანალოგი ტრიგონომეტრიაში!

Ისე, როგორ გამოითვლება კუთხეები წრეზე?გასაკეთებელი არაფერია, ჯერ სწორედ ეს წრე მოგვიწევს.

მე დავხატავ ამ ლამაზ სურათს:

ძალიან ჰგავს წინა გაკვეთილის სურათებს. არის ცულები, არის წრე, არის კუთხე. მაგრამ არის ახალი ინფორმაციაც.

მე ასევე დავამატე რიცხვები 0°, 90°, 180°, 270° და 360° ღერძებზე. ახლა ეს უფრო საინტერესოა.) რა არის ეს რიცხვები? სწორად! ეს არის ჩვენი ფიქსირებული მხრიდან გაზომილი კუთხეების მნიშვნელობები, რომლებიც ეცემა კოორდინატთა ღერძებზე.შეგახსენებთ, რომ კუთხის ფიქსირებული მხარე ყოველთვის მყარად არის მიმაგრებული დადებით ნახევარღერძზე OX. და ტრიგონომეტრიაში ნებისმიერი კუთხე იზომება ამ ნახევრადღერძიდან. ირონიულად უნდა გვახსოვდეს კუთხეების ეს ძირითადი წარმოშობა. ცულები კი - სწორი კუთხით იკვეთება, არა? ასე რომ, ჩვენ ვამატებთ 90 ° თითოეულ კვარტალში.

და კიდევ დაემატა წითელი ისარი. პლუსით. წითელი მიზანმიმართულად მიიპყრო თვალი. და კარგად ჩამრჩა მეხსიერებაში. ამისთვის საიმედოდ უნდა დაიმახსოვროთ.) რას ნიშნავს ეს ისარი?

ასე გამოდის, თუ ჩვენს კუთხეს მოვუხვევთ პლუს ისარი(საათის ისრის საწინააღმდეგო მიმართულებით, მეოთხედების ნუმერაციის დროს), შემდეგ კუთხე დადებითად ჩაითვლება!ფიგურაში ნაჩვენებია კუთხე +45°, როგორც მაგალითი. სხვათა შორის, გთხოვთ გაითვალისწინოთ, რომ ღერძული კუთხეები 0°, 90°, 180°, 270° და 360° ასევე გადახვევა ზუსტად პლუსშია! წითელი ისრით.

ახლა გადავხედოთ სხვა სურათს:

აქ თითქმის ყველაფერი იგივეა. ღერძებზე მხოლოდ კუთხეებია დანომრილი შებრუნებული.საათის ისრის მიმართულებით. და მათ აქვთ მინუს ნიშანი.) ლურჯი ისარი. ასევე მინუსით. ეს ისარი არის წრეზე კუთხეების უარყოფითი წაკითხვის მიმართულება. ის გვაჩვენებს, რომ თუ გადავდებთ ჩვენს კუთხეს საათის ისრის მიმართულებით, მაშინ კუთხე ჩაითვლება უარყოფითად.მაგალითად, მე ვაჩვენე კუთხე -45°.

სხვათა შორის, გთხოვთ გაითვალისწინოთ, რომ კვარტლების ნუმერაცია არასოდეს იცვლება! არ აქვს მნიშვნელობა კუთხეებს პლიუსში მოვახვევთ თუ მინუსს. ყოველთვის მკაცრად საათის ისრის საწინააღმდეგოდ.)

გახსოვდეთ:

1. კუთხეების დათვლის დასაწყისი არის ОХ დადებითი ნახევარღერძიდან. საათის მიხედვით - "მინუს", საათის საწინააღმდეგოდ - "პლუს".

2. კვარტლების ნუმერაცია ყოველთვის არის საათის ისრის საწინააღმდეგოდ, მიუხედავად კუთხეების გამოთვლის მიმართულებისა.

სხვათა შორის, 0°, 90°, 180°, 270°, 360° ღერძებზე კუთხეების ხელმოწერა, ყოველ ჯერზე წრის დახატვაზე, საერთოდ არ არის მოთხოვნა. ეს არის მხოლოდ არსის გასაგებად. მაგრამ ეს რიცხვები უნდა იყოს წარმოდგენილი შენს თავშიტრიგონომეტრიაში რაიმე პრობლემის გადაჭრისას. რატომ? დიახ, რადგან ეს ელემენტარული ცოდნა იძლევა პასუხს ბევრ სხვა კითხვაზე ყველა ტრიგონომეტრიაში! ყველაზე მნიშვნელოვანი კითხვაა რომელ კვარტალში ეცემა ის კუთხე, რომელიც ჩვენ გვაინტერესებს? დაიჯერეთ თუ არა, ამ კითხვაზე სწორი პასუხი ხსნის ტრიგონომეტრიის ყველა სხვა პრობლემის ლომის წილს. ამ მნიშვნელოვან გაკვეთილზე (კუთხეების განაწილება მეოთხედებში) შევეხებით იმავე გაკვეთილზე, ოღონდ ცოტა მოგვიანებით.

კოორდინატთა ღერძებზე მდებარე კუთხეების მნიშვნელობები (0°, 90°, 180°, 270° და 360°) უნდა დაიმახსოვროთ! დაიმახსოვრე მტკიცედ, ავტომატიზმამდე. და პლუსშიც და მინუსშიც.

მაგრამ ამ მომენტიდან იწყება პირველი სიურპრიზები. და მათთან ერთად ჩემთან მიმართული რთული კითხვები, დიახ ...) და რა მოხდება, თუ წრეზე უარყოფითი კუთხე ემთხვევა დადებითს?თურმე იგივე წერტილიწრეზე შეიძლება აღინიშნოს დადებითი კუთხე, ხოლო უარყოფითი ???

საკმაოდ სწორია! ასეც არის.) მაგალითად, წრეზე +270° დადებითი კუთხე იკავებს იგივე პოზიცია , რომელიც არის უარყოფითი კუთხე -90°. ან, მაგალითად, წრეზე +45° დადებითი კუთხე მიიღებს იგივე პოზიცია , რომელიც არის უარყოფითი კუთხე -315°.

ჩვენ ვუყურებთ შემდეგ სურათს და ვხედავთ ყველაფერს:

ანალოგიურად, +150° დადებითი კუთხე წავა იქ, სადაც უარყოფითი კუთხე -210°, დადებითი კუთხე +230° - იმავე ადგილას, სადაც უარყოფითი კუთხე -130°. Და ასე შემდეგ…

და ახლა რა შემიძლია გავაკეთო? ზუსტად როგორ დავთვალოთ კუთხეები, თუ შესაძლებელია ასე და ისე? რამდენად სწორად?

პასუხი: მაინც სწორია!მათემატიკა არ კრძალავს კუთხეების დათვლის ორი მიმართულებიდან არცერთს. და კონკრეტული მიმართულების არჩევანი დამოკიდებულია მხოლოდ დავალებაზე. თუ დავალება უბრალო ტექსტში არაფერს ამბობს კუთხის ნიშნის შესახებ (როგორიცაა „განსაზღვრე ყველაზე დიდი უარყოფითიკუთხე"და ა.შ.), შემდეგ ჩვენ ვმუშაობთ ჩვენთვის ყველაზე მოსახერხებელ კუთხეებით.

რა თქმა უნდა, მაგალითად, ისეთ მაგარ თემებში, როგორიცაა ტრიგონომეტრიული განტოლებები და უტოლობა, კუთხეების გამოთვლის მიმართულებამ შეიძლება დიდი გავლენა იქონიოს პასუხზე. და შესაბამის თემებში განვიხილავთ ამ ხარვეზებს.

გახსოვდეთ:

წრის ნებისმიერი წერტილი შეიძლება აღინიშნოს როგორც დადებითი, ასევე უარყოფითი კუთხით. ნებისმიერს! რაც გვინდა.

ახლა მოდით ვიფიქროთ ამაზე. ჩვენ გავარკვიეთ, რომ 45° კუთხე ზუსტად იგივეა, რაც -315°? როგორ გავიგე იგივე 315-ის შესახებ° ? ვერ გამოიცანით? დიახ! სრული შემობრუნების გზით.) 360 °-ში. გვაქვს 45° კუთხე. რამდენი აკლია სრულ შემობრუნებამდე? გამოვაკლოთ 45° 360-დან° - აქ მივიღებთ 315° . ჩვენ ვახვევთ უარყოფითი მიმართულებით - და ვიღებთ კუთხეს -315 °. ჯერ კიდევ გაუგებარია? შემდეგ კვლავ შეხედეთ სურათს ზემოთ.

და ეს ყოველთვის უნდა გაკეთდეს დადებითი კუთხეების უარყოფითად თარგმნისას (და პირიქით) - დახაზეთ წრე, შენიშნეთ შესახებმოცემული კუთხით, ჩვენ განვიხილავთ რამდენი გრადუსი აკლია სრულ შემობრუნებამდე და მივახვევთ მიღებულ განსხვავებას საპირისპირო მიმართულებით. და ეს არის ის.)

კიდევ რა არის საინტერესო იმ კუთხეებში, რომლებიც ერთსა და იმავე პოზიციას იკავებენ წრეზე, როგორ ფიქრობთ? და ის ფაქტი, რომ ასეთი კუთხეები ზუსტად იგივე სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი! Ყოველთვის არის!

Მაგალითად:

Sin45° = sin (-315°)

Cos120° = cos(-240°)

Tg249° = tg (-111°)

Ctg333° = ctg (-27°)

და ახლა ეს ძალიან მნიშვნელოვანია! Რისთვის? დიახ, ყველა ერთი და იგივე!) გამონათქვამების გასამარტივებლად. გამონათქვამების გამარტივებისთვის არის წარმატებული გადაწყვეტის მთავარი პროცედურა ნებისმიერიდავალებები მათემატიკაში. და ასევე ტრიგონომეტრია.

ასე რომ, ჩვენ გავარკვიეთ წრეზე კუთხეების დათვლის ზოგადი წესი. კარგად, თუ ჩვენ აქ მივანიშნებდით სრულ მოხვევებზე, დაახლოებით მეოთხედებზე, მაშინ დრო იქნებოდა ამ კუთხეების გადახვევა და დახატვა. დავხატოთ?)

დავიწყოთ იმით დადებითიკუთხეები. მათი დახატვა უფრო ადვილი იქნება.

დახაზეთ კუთხეები ერთი ბრუნვის ფარგლებში (0°-დან 360°-მდე).

დავხატოთ, მაგალითად, კუთხე 60°. აქ ყველაფერი მარტივია, არაფრის გარეშე. ვხატავთ კოორდინატთა ღერძებს, წრეს. შეგიძლიათ პირდაპირ ხელით, ყოველგვარი კომპასისა და სახაზავის გარეშე. ჩვენ ვხატავთ სქემატურად _ თქვენთან შედგენა არ გვაქვს. არ არის საჭირო GOST-ების დაცვა, ისინი არ დაისჯებიან.)

თქვენ შეგიძლიათ (თვითონ) მონიშნოთ კუთხეების მნიშვნელობები ღერძებზე და მიუთითოთ ისარი მიმართულებით საათის საწინააღმდეგოდ.ბოლოს და ბოლოს, ჩვენ ვაპირებთ ფულის დაზოგვას, როგორც პლუსს?) თქვენ არ შეგიძლიათ ამის გაკეთება, მაგრამ თქვენ უნდა შეინახოთ ყველაფერი თქვენს თავში.

ახლა კი კუთხის მეორე (მოძრავი) მხარეს ვხატავთ. რომელი მეოთხედი? პირველში, რა თქმა უნდა! 60 გრადუსისთვის მკაცრად არის 0°-დან 90°-მდე. ასე რომ, ჩვენ ვხატავთ პირველ მეოთხედში. კუთხით შესახებ 60 გრადუსით ფიქსირებულ მხარეს. როგორ დავთვალოთ შესახებ 60 გრადუსი პროტრატორის გარეშე? მარტივად! 60° არის მართი კუთხის ორი მესამედი!წრის პირველ მეოთხედს ძალაუნებურად ვყოფთ სამ ნაწილად, ჩვენთვის ორ მესამედს ვიღებთ. და ჩვენ ვხატავთ ... რეალურად რამდენს მივიღებთ იქ (თუ პროტრაქტორს მივამაგრებთ და გავზომავთ) - 55 გრადუსი თუ 64 - არ აქვს მნიშვნელობა! მნიშვნელოვანია, რომ ჯერ კიდევ სადღაც დაახლოებით 60 °.

ჩვენ ვიღებთ სურათს:

Სულ ეს არის. და არც იარაღები იყო საჭირო. ჩვენ ვავითარებთ თვალს! ის გამოგადგებათ გეომეტრიის ამოცანებში.) ეს არაკეთილსინდისიერი ნახატი შეიძლება იყოს შეუცვლელი, როდესაც თქვენ გჭირდებათ ნაჩქარევად დახაზოთ წრე და კუთხე, სილამაზეზე ფიქრის გარეშე. ოღონდ ამავდროულად ნაწერი უფლება, უშეცდომოდ, ყველა საჭირო ინფორმაციით. მაგალითად, როგორც დამხმარე საშუალება ტრიგონომეტრიული განტოლებებისა და უტოლობების ამოხსნაში.

ახლა დავხატოთ კუთხე, მაგალითად, 265°. გამოიცანით სად შეიძლება იყოს? ისე, გასაგებია, რომ არც პირველ კვარტალში და არც მეორეში: ისინი მთავრდება 90 და 180 გრადუსზე. შეგიძლიათ იფიქროთ, რომ 265° არის 180° პლუს კიდევ 85°. ანუ, უარყოფით ნახევარღერძს უნდა დაემატოს OX (სადაც 180 °). შესახებ 85°. ან, კიდევ უფრო ადვილია იმის გამოცნობა, რომ 265 ° არ აღწევს ნეგატიურ ნახევრად ღერძს OY (სადაც 270 °) ზოგიერთი სამწუხარო 5 °. ერთი სიტყვით, მესამე მეოთხედში იქნება ეს კუთხე. OY უარყოფით ღერძთან ძალიან ახლოს, 270 გრადუსამდე, მაგრამ მაინც მესამეში!

დახატვა:

ისევ და ისევ, აქ აბსოლუტური სიზუსტე არ არის საჭირო. მოდით, სინამდვილეში ეს კუთხე აღმოჩნდა, ვთქვათ, 263 გრადუსი. მაგრამ ყველაზე მნიშვნელოვანი კითხვა (რა მეოთხედი?)ჩვენ სწორად ვუპასუხეთ. რატომ არის ეს ყველაზე მნიშვნელოვანი კითხვა? დიახ, რადგან ნებისმიერი ნამუშევარი კუთხით ტრიგონომეტრიაში (მივხაზავთ თუ არა ამ კუთხეს) სწორედ ამ კითხვის პასუხით იწყება! Ყოველთვის არის. თუ თქვენ უგულებელყოფთ ამ კითხვას ან ცდილობთ მას გონებრივად უპასუხოთ, მაშინ შეცდომები თითქმის გარდაუვალია, დიახ... გჭირდებათ ეს?

გახსოვდეთ:

ნებისმიერი სამუშაო კუთხით (მათ შორის სწორედ ამ კუთხის დახატვა წრეზე) ყოველთვის იწყება მეოთხედის განსაზღვრით, რომელშიც ეს კუთხე ეცემა.

ახლა, ვიმედოვნებ, რომ სწორად დახაზავთ კუთხეებს, მაგალითად, 182°, 88°, 280°. AT სწორიმეოთხედი. მესამეში, პირველში და მეოთხეში, თუ რამე ...)

მეოთხე მეოთხედი მთავრდება 360° კუთხით. ეს არის ერთი სრული შემობრუნება. წიწაკა ნათელია, რომ ეს კუთხე იკავებს იმავე პოზიციას წრეზე, როგორც 0 ° (ანუ საცნობარო წერტილი). მაგრამ კუთხეები ამით არ მთავრდება, ჰო...

რა ვუყოთ 360°-ზე მეტ კუთხეებს?

"არსებობს ასეთი რამ?"- გეკითხებით. არსებობენ, როგორ! ეს ხდება, მაგალითად, კუთხე 444 °. და ზოგჯერ, ვთქვათ, კუთხე 1000 °. არსებობს ყველანაირი კუთხე.) მხოლოდ ვიზუალურად, ასეთი ეგზოტიკური კუთხეები აღიქმება ოდნავ უფრო რთულად, ვიდრე ჩვეულებრივი კუთხეები ერთ შემობრუნებაში. მაგრამ თქვენ ასევე უნდა შეძლოთ ასეთი კუთხეების დახატვა და გამოთვლა, დიახ.

წრეზე ასეთი კუთხეების სწორად დახატვისთვის, თქვენ უნდა გააკეთოთ იგივე - გაარკვიეთ რომელ კვარტალში ეცემა ინტერესის კუთხე. აქ კვარტალის ზუსტად განსაზღვრის შესაძლებლობა ბევრად უფრო მნიშვნელოვანია, ვიდრე კუთხეებისთვის 0 °-დან 360 °-მდე! კვარტალის დადგენის პროცესი მხოლოდ ერთი ნაბიჯით რთულდება. რომელს, მალე ნახავთ.

ასე, მაგალითად, უნდა გავარკვიოთ რომელ მეოთხედში ეცემა კუთხე 444°. ვიწყებთ ტრიალს. სად? როგორც პლუსი, რა თქმა უნდა! მათ დადებითი კუთხე მოგვცეს! +444°. ვტრიალებთ, ვტრიალებთ... ერთი შემობრუნება გადავუხვიეთ - მივაღწიეთ 360 °-ს.

რამდენი დარჩა 444°-მდე?ჩვენ ვითვლით დარჩენილ კუდს:

444°-360° = 84°.

ასე რომ, 444° არის ერთი სრული შემობრუნება (360°) პლუს კიდევ 84°. ცხადია, ეს პირველი კვარტალია. ასე რომ, კუთხე 444° ეცემა პირველ კვარტალში.ნახევრად გაკეთებული.

ახლა რჩება ამ კუთხის გამოსახვა. Როგორ? Ძალიან მარტივი! ჩვენ ვაკეთებთ ერთ სრულ შემობრუნებას წითელი (პლუს) ისრის გასწვრივ და ვამატებთ კიდევ 84 °.

Ამგვარად:

აქ ნახატი არ დავაბინძურე - მოაწერეთ კვარტლები, დახაზეთ კუთხეები ცულებზე. მთელი ეს სიკეთე დიდი ხანი უნდა ყოფილიყო ჩემს თავში.)

მაგრამ მე "ლოკოკინით" ან სპირალით ვაჩვენე, თუ როგორ იქმნება ზუსტად 444 ° კუთხე 360 ° და 84 ° კუთხიდან. წერტილოვანი წითელი ხაზი არის ერთი სრული შემობრუნება. რომელზედაც დამატებით ხრახნიან 84° (მყარი ხაზი). სხვათა შორის, გთხოვთ გაითვალისწინოთ, რომ თუ ეს ძალიან სრული შემობრუნება განადგურდება, მაშინ ეს არანაირად არ იმოქმედებს ჩვენი კუთხის პოზიციაზე!

მაგრამ ეს მნიშვნელოვანია! კუთხის პოზიცია 444° სრულიად ემთხვევაკუთხის პოზიციით 84°. სასწაულები არ არის, ეს უბრალოდ ხდება.)

შესაძლებელია არა ერთი სრული მობრუნების, არამედ ორი ან მეტის გაუქმება?

Რატომაც არა? თუ კუთხე მძიმეა, მაშინ ეს არ არის მხოლოდ შესაძლებელი, არამედ აუცილებელიც კი! კუთხე არ შეიცვლება! უფრო ზუსტად, თავად კუთხე, რა თქმა უნდა, შეიცვლება სიდიდით. მაგრამ მისი პოზიცია წრეზე – არავითარ შემთხვევაში!) ამიტომ ისინი სავსეიმპულსი, რომ რამდენი ასლიც არ უნდა დაამატო, რამდენიც არ უნდა გამოაკლო, მაინც იმავე წერტილს მიაღწევ. სასიამოვნოა, არა?

გახსოვდეთ:

თუ რომელიმე კუთხეს დავუმატებთ (გამოვაკლებთ). მთლიანისრული რევოლუციების რაოდენობა, თავდაპირველი კუთხის პოზიცია წრეზე არ შეიცვლება!

Მაგალითად:

რომელ მეოთხედში ეცემა კუთხე 1000°?

Არაა პრობლემა! ჩვენ განვიხილავთ რამდენი სრული რევოლუცია ზის ათას გრადუსში. ერთი რევოლუცია არის 360°, მეორე უკვე 720°, მესამე არის 1080°... გაჩერდი! ბიუსტი! ასე რომ, 1000 ° კუთხით ზის ორისრული ბრუნვა. გადააგდეთ ისინი 1000°-დან და გამოთვალეთ დარჩენილი ნაწილი:

1000° - 2 360° = 280°

ასე რომ, კუთხის პოზიცია წრეზე 1000° იგივე, რომელიც იგივეა, რაც კუთხე 280°. ვისთანაც უკვე ბევრად სასიამოვნოა მუშაობა.) და სად ვარდება ეს კუთხე? ის ხვდება მეოთხე კვარტალში: 270° (უარყოფითი ნახევრად ღერძი OY) პლუს კიდევ ათი.

დახატვა:

აქ აღარ დავხატე ორი სრული შემობრუნება წერტილოვანი სპირალით: მტკივნეულად გრძელი გამოდის. უბრალოდ დახატე დანარჩენი კუდი ნულიდან, გადაყრა ყველადამატებითი მოხვევები. თითქოს არც არსებობდნენ.)

Კიდევ ერთხელ. კარგი თვალსაზრისით, კუთხეები 444° და 84°, ასევე 1000° და 280° განსხვავებულია. მაგრამ სინუსისთვის, კოსინუსისთვის, ტანგენსისთვის და კოტანგენსისთვის, ეს კუთხეებია იგივე!

როგორც ხედავთ, 360°-ზე დიდ კუთხეებთან მუშაობისთვის საჭიროა განსაზღვროთ რამდენი სრული ბრუნი ზის მოცემულ დიდ კუთხეში. ეს არის ძალიან დამატებითი ნაბიჯი, რომელიც წინასწარ უნდა გაკეთდეს ასეთ კუთხეებთან მუშაობისას. არაფერი რთული, არა?

სრული მოხვევის ჩამოგდება, რა თქმა უნდა, სასიამოვნო გამოცდილებაა.) მაგრამ პრაქტიკაში, აბსოლუტურად კოშმარული კუთხით მუშაობისას, სირთულეებიც წარმოიქმნება.

Მაგალითად:

რომელ მეოთხედში ეცემა კუთხე 31240°?

და რა, ბევრჯერ დავამატებთ 360 გრადუსს? შესაძლებელია, თუ განსაკუთრებით არ დაიწვა. მაგრამ ჩვენ არ შეგვიძლია მხოლოდ დავამატოთ.) ასევე შეგვიძლია გავყოთ!

მოდით გავყოთ ჩვენი უზარმაზარი კუთხე 360 გრადუსად!

ამ მოქმედებით ჩვენ უბრალოდ გავარკვევთ რამდენი სრული რევოლუცია იმალება ჩვენს 31240 გრადუსში. შეგიძლიათ გააზიაროთ კუთხე, შეგიძლიათ (ყურში ჩასჩურჩულოთ :)) კალკულატორზე.)

ჩვენ ვიღებთ 31240:360 = 86.777777….

ის, რომ რიცხვი წილადი აღმოჩნდა, არ არის საშინელი. ჩვენ ვართ მხოლოდ მთლიანიმე მაინტერესებს ბრუნვები! ამიტომ, არ არის საჭირო ბოლომდე გაყოფა.)

ასე რომ, ჩვენს შიგნეულ კუთხეში არის 86 სრული რევოლუცია. საშინელება…

გრადუსებში იქნება86 360° = 30960°

Ამგვარად. ეს არის რამდენი გრადუსი შეიძლება უმტკივნეულოდ გადმოაგდოთ მოცემული 31240 ° კუთხიდან. რჩება:

31240° - 30960° = 280°

ყველაფერი! კუთხის პოზიცია 31240° სრულად იდენტიფიცირებულია! იმავე ადგილას, როგორც 280 °. იმათ. მეოთხე მეოთხედი.) როგორც ჩანს, ეს კუთხე ადრე უკვე გამოვხატეთ? როდის იყო დახატული 1000° კუთხე?) იქ ჩვენც 280 გრადუსით წავედით. დამთხვევა.)

ასე რომ, ამბის მორალი ასეთია:

თუ ჩვენ გვეძლევა საშინელი, მძიმე კუთხე, მაშინ:

1. დაადგინეთ რამდენი სრული რევოლუცია ზის ამ კუთხეში. ამისათვის გაყავით საწყისი კუთხე 360-ით და გადააგდეთ წილადი ნაწილი.

2. განვიხილავთ რამდენი გრადუსია მიღებულ ბრუნთა რაოდენობაში. ამისათვის გაამრავლეთ რევოლუციების რაოდენობა 360-ზე.

3. გამოაკლეთ ეს ბრუნვები თავდაპირველი კუთხიდან და იმუშავეთ ჩვეულებრივი კუთხით 0°-დან 360°-მდე დიაპაზონში.

როგორ ვიმუშაოთ უარყოფით კუთხეებთან?

Არაა პრობლემა! ისევე, როგორც პოზიტიურებთან, მხოლოდ ერთი განსხვავება. Რა? დიახ! თქვენ უნდა მოაბრუნოთ კუთხეები საპირისპირო მხარეს, მინუს! საათის ისრის მიმართულებით.)

დავხატოთ, მაგალითად, კუთხე -200°. თავიდან ყველაფერი ჩვეულია დადებითი კუთხისთვის - ცულები, წრე. მინუსით დავხატოთ ლურჯი ისარი და ღერძებზე კუთხეები სხვანაირად მოვაწეროთ. მათი დათვლა, რა თქმა უნდა, უარყოფითი მიმართულებითაც მოუწევს. ეს იქნება ყველა ერთი და იგივე კუთხე, გადადგმული 90°-ით, მაგრამ დათვლილი საპირისპირო მიმართულებით, მინუს: 0°, -90°, -180°, -270°, -360°.

სურათი ასე გამოიყურება:

ნეგატიურ კუთხებთან მუშაობისას ხშირად ჩნდება უმნიშვნელო დაბნეულობა. Როგორ თუ?! გამოდის, რომ ერთი და იგივე ღერძი ორივეა, ვთქვათ, +90° და -270°? არა, აქ რაღაც არასწორია...

დიახ, ყველაფერი სუფთა და გამჭვირვალეა! ყოველივე ამის შემდეგ, ჩვენ უკვე ვიცით, რომ წრის ნებისმიერ წერტილს შეიძლება ეწოდოს როგორც დადებითი, ასევე უარყოფითი კუთხე! აბსოლუტურად ნებისმიერი. მათ შორის ზოგიერთ კოორდინატულ ღერძზე. ჩვენს შემთხვევაში გვჭირდება უარყოფითიკუთხეების გაანგარიშება. ასე რომ, ჩვენ ყველა კუთხეს მინუსამდე ვხსნით.)

ახლა -200°-ის სწორი კუთხის დახატვა არ არის პრობლემა. ეს არის -180 ° და მინუსკიდევ 20 °. ჩვენ ვიწყებთ გრაგნილს ნულიდან მინუსამდე: ვფრინავთ მეოთხე კვარტალში, მესამეც წარსულია, მივაღწევთ -180 °. სად დავამარცხოთ დარჩენილი ოცი? დიახ, ყველაფერი რიგზეა! საათის მიხედვით.) მთლიანი კუთხე -200° ეცემა მეორემეოთხედი.

ახლა გესმით, რამდენად მნიშვნელოვანია კოორდინატთა ღერძებზე კუთხეების დამახსოვრება?

კუთხეები კოორდინატთა ღერძებზე (0°, 90°, 180°, 270°, 360°) ზუსტად უნდა დაიმახსოვროთ, რათა ზუსტად განისაზღვროს მეოთხედი, სადაც ეცემა კუთხე!

და თუ კუთხე დიდია, რამდენიმე სრული შემობრუნებით? Ყველაფერი კარგადაა! რა განსხვავებაა, სად არის შემობრუნებული ეს სრული სიჩქარე - პლუსში თუ მინუსში? წრეზე წერტილი არ ცვლის მის პოზიციას!

Მაგალითად:

რომელ კვადრატში ეცემა კუთხე -2000°?

Ერთი და იგივე! დასაწყისისთვის, ჩვენ განვიხილავთ რამდენი სრული რევოლუცია ზის ამ ბოროტ კუთხეში. ნიშნებში რომ არ ავურიოთ, ჯერ მინუსს თავი დავანებოთ და 2000 გავყოთ 360-ზე. ვიღებთ 5-ს კუდით. კუდი ჯერ არ გვაწუხებს, კუთხის დახატვისას ცოტა მოგვიანებით ჩავთვლით. Ჩვენ გვჯერა ხუთისრული რევოლუციები გრადუსებში:

5 360° = 1800°

ვოტ. ეს არის რამდენი დამატებითი გრადუსი შეგიძლიათ უსაფრთხოდ გადააგდოთ ჩვენი კუთხიდან ჯანმრთელობისთვის ზიანის მიყენების გარეშე.

ჩვენ ვითვლით დარჩენილ კუდს:

2000° – 1800° = 200°

და ახლა თქვენ ასევე შეგიძლიათ გახსოვდეთ მინუსის შესახებ.) სად დავაკრავთ კუდს 200 °? მინუსი, რა თქმა უნდა! ჩვენ გვეძლევა უარყოფითი კუთხე.)

2000° = -1800° - 200°

ასე რომ, ჩვენ ვხატავთ კუთხეს -200 °, მხოლოდ დამატებითი შემობრუნების გარეშე. ახლახან დავხატე, მაგრამ, ასე იყოს, კიდევ ერთხელ დავხატავ. Ხელით.

წიწაკა ნათელია, რომ მოცემული კუთხე -2000 °, ისევე როგორც -200 °, მოდის მეორე მეოთხედი.

ასე რომ, ჩვენ წრეზე ვტრიალებთ ... ბოდიში ... ულვაშებზე:

თუ ძალიან დიდი უარყოფითი კუთხეა მოცემული, მაშინ მასთან მუშაობის პირველი ნაწილი (სრული ბრუნების რაოდენობის პოვნა და მათი გაუქმება) იგივეა, რაც დადებითი კუთხით მუშაობისას. მინუს ნიშანი გადაწყვეტის ამ ეტაპზე არანაირ როლს არ თამაშობს. ნიშანი მხედველობაში მიიღება მხოლოდ ბოლოს, სრული მობრუნების მოხსნის შემდეგ დარჩენილ კუთხესთან მუშაობისას.

როგორც ხედავთ, წრეზე უარყოფითი კუთხეების დახატვა არ არის უფრო რთული, ვიდრე დადებითი.

ყველაფერი იგივეა, მხოლოდ სხვა მიმართულებით! საათობრივად!

ახლა კი - ყველაზე საინტერესო! ჩვენ დავფარეთ დადებითი კუთხეები, უარყოფითი კუთხეები, დიდი კუთხეები, პატარა კუთხეები - სრული დიაპაზონი. ჩვენ ასევე გავარკვიეთ, რომ წრის ნებისმიერ წერტილს შეიძლება ეწოდოს დადებითი და უარყოფითი კუთხე, ჩვენ გადავაგდეთ სრული მოხვევები ... არ ფიქრობთ? უნდა გადაიდოს...

დიახ! წრის რომელ წერტილსაც აიღებთ, ის შეესაბამება გაუთავებელი კუთხეები! დიდი და არც ისე, დადებითი და უარყოფითი - ყველას! და განსხვავება ამ კუთხეებს შორის იქნება მთლიანი სრული შემობრუნების რაოდენობა. Ყოველთვის არის! ასე რომ, ტრიგონომეტრიული წრე მოწყობილია, დიახ ...) ამიტომ საპირისპიროამოცანაა ვიპოვოთ კუთხე ცნობილი სინუსის / კოსინუსის / ტანგენტის / კოტანგენსით - ამოხსნილია ორაზროვანი. და ბევრად უფრო რთული. პირდაპირი პრობლემისგან განსხვავებით - იპოვონ მისი ტრიგონომეტრიული ფუნქციების მთელი სიმრავლე მოცემული კუთხისთვის. და ტრიგონომეტრიის უფრო სერიოზულ თემებში ( თაღები, ტრიგონომეტრიული განტოლებებიდა უთანასწორობები ) ამ ჩიპს მუდმივად ვაწყდებით. შეჩვევა.)

1. რომელ მეოთხედში ეცემა კუთხე -345°?

2. რომელ მეოთხედში ეცემა კუთხე 666°?

3. რომელ მეოთხედში ეცემა კუთხე 5555°?

4. რომელ მეოთხედში ეცემა -3700° კუთხე?

5. რა არის ნიშანიcos999°?

6. რა არის ნიშანიctg999°?

და მუშაობდა? მშვენიერია! Პრობლემაა? Შემდეგ შენ.

პასუხები:

1. 1

2. 4

3. 2

4. 3

5. "+"

6. "-"

ამჯერად პასუხები თანმიმდევრობით, ტრადიციის დარღვევით არის გაცემული. რადგან მხოლოდ ოთხი მეოთხედია და მხოლოდ ორი ნიშანია. არ გაიქცევი...)

შემდეგ გაკვეთილზე ვისაუბრებთ რადიანებზე, იდუმალ რიცხვზე „პი“-ზე, ვისწავლით თუ როგორ გადავიტანოთ რადიანები მარტივად და მარტივად ხარისხებად და პირიქით. და გაგვიკვირდება, თუ აღმოვაჩენთ, რომ ეს მარტივი ცოდნა და უნარებიც კი უკვე სრულიად საკმარისი იქნება იმისათვის, რომ წარმატებით გადავჭრათ ტრიგონომეტრიაში მრავალი არატრივიალური პრობლემა!

მაგალითი 1

იპოვეთ კუთხის რადიანის ზომა, რომელიც ტოლია ა) 40°, ბ) 120°, გ) 105°

ა) 40° = 40 π / 180 = 2π/9

ბ) 120° = 120 π/180 = 2π/3

გ) 105° = 105 π/180 = 7π/12

მაგალითი 2

იპოვეთ რადიანებით გამოხატული კუთხის გრადუსის ზომა ა) π/6, ბ) π/9, გ) 2 π/3

ა) π/6 = 180°/6 = 30°

ბ) π/9 = 180°/9 = 20°

გ) 2π/3 = 2 180°/6 = 120°

სინუსის, კოსინუსის, ტანგენსის და კოტანგენტის განმარტება

მართკუთხა სამკუთხედის t მწვავე კუთხის სინუსი უდრის მოპირდაპირე ფეხის შეფარდებას ჰიპოტენუზასთან (ნახ. 1):

მართკუთხა სამკუთხედის t მწვავე კუთხის კოსინუსი უდრის მიმდებარე ფეხის შეფარდებას ჰიპოტენუზასთან (ნახ. 1):

ეს განმარტებები ეხება მართკუთხა სამკუთხედს და არის ამ ნაწილში წარმოდგენილი განმარტებების განსაკუთრებული შემთხვევები.

იგივე მართკუთხა სამკუთხედი მოვათავსოთ რიცხვით წრეში (სურ. 2).

ჩვენ ვხედავთ, რომ ფეხი ბუდრის გარკვეულ მნიშვნელობას წ Y-ღერძზე (y-ღერძი), ფეხი აუდრის გარკვეულ მნიშვნელობას x x-ღერძზე (აბსცისა). ჰიპოტენუზა თანწრის რადიუსის ტოლი (R).

ამრიგად, ჩვენი ფორმულები სხვა ფორმას იღებს.

ვინაიდან b = წ, a = x, c = R, შემდეგ:

y x
sin t = -- , cos t = --.
რ რ

სხვათა შორის, მაშინ, ბუნებრივია, ტანგენსის და კოტანგენტის ფორმულებიც განსხვავებულ ფორმას იღებს.

ვინაიდან tg t \u003d b / a, ctg t \u003d a / b, მაშინ სხვა განტოლებები ასევე მართალია:

tg t = წ/x,

ctg= x/წ.

მაგრამ ისევ სინუსსა და კოსინუსს. საქმე გვაქვს ციფრულ წრესთან, რომელშიც რადიუსი არის 1. ასე რომ, გამოდის:

წ
sin t = -- = წ,
1

x
cos t = -- = x.
1

ასე რომ, მივედით ტრიგონომეტრიული ფორმულების მესამე, უფრო მარტივ ფორმამდე.

ეს ფორმულები გამოიყენება არა მხოლოდ მწვავე კუთხისთვის, არამედ ნებისმიერი სხვა კუთხისთვის (ბუნდოვანი ან განვითარებული).

განმარტებები და ფორმულები cos t, sin t, tg t, ctg t.

კიდევ ერთი ფორმულა გამომდინარეობს ტანგენტისა და კოტანგენტის ფორმულებიდან:

რიცხვითი წრის განტოლებები.

სინუსის, კოსინუსის, ტანგენსის და კოტანგენტის ნიშნები წრის მეოთხედებში:

	1 მეოთხედი	მე-2 მეოთხედი	მე-3 მეოთხედი	მე-4 მეოთხედი
cos ტ	+	–	–	+
ცოდვა თ	+	+	–	–
tg t, ctg t	+	–	+	–

რიცხვითი წრის ძირითადი წერტილების კოსინუსი და სინუსი:

როგორ დავიმახსოვროთ რიცხვითი წრის ძირითადი წერტილების კოსინუსების და სინუსების მნიშვნელობები.

უპირველეს ყოვლისა, თქვენ უნდა იცოდეთ, რომ რიცხვების თითოეულ წყვილში კოსინუსის მნიშვნელობები პირველია, სინუსური მნიშვნელობები“ მეორე.

1) ყურადღება მიაქციეთ: რიცხვითი წრის წერტილების მთელი ნაკრებისთვის საქმე გვაქვს მხოლოდ ხუთ რიცხვთან (მოდულში):

1 √2 √3
0; -; --; --; 1.
2 2 2

გააკეთეთ ეს "აღმოჩენა" თქვენთვის - და თქვენ მოგიხსნით რიცხვების სიმრავლის ფსიქოლოგიურ შიშს: სინამდვილეში მხოლოდ ხუთი მათგანია.

2) დავიწყოთ მთელი რიცხვებით 0 და 1. ისინი მხოლოდ კოორდინატთა ღერძებზეა.

არ არის საჭირო ზეპირად სწავლა, მაგალითად, სად აქვს მოდულში კოსინუსს ერთეული და სად 0.

ღერძის ბოლოებზე კოსინუსები(ცულები X), რა თქმა უნდა, კოსინუსები არის მოდულო 1და სინუსები არის 0.

ღერძის ბოლოებზე სინუსები(ცულები ზე) სინუსები არის მოდულო 1და კოსინუსები არის 0.

ახლა ნიშნების შესახებ. ნულს არ აქვს ნიშანი. რაც შეეხება 1-ს - აქ თქვენ უბრალოდ უნდა გახსოვდეთ უმარტივესი რამ: მე-7 კლასის კურსიდან იცით, რომ ღერძზე Xკოორდინატთა სიბრტყის ცენტრის მარჯვნივ - დადებითი რიცხვები, მარცხნივ - უარყოფითი; ღერძზე ზედადებითი რიცხვები ცენტრიდან ადის, უარყოფითი ქვევით. და მაშინ არ შეიძლება შეცდეთ 1 ნიშნით.

3) ახლა მოდით გადავიდეთ წილადის მნიშვნელობებზე.

წილადების ყველა მნიშვნელში - ერთი და იგივე რიცხვი 2. არ შევცდებით რა დავწეროთ მნიშვნელში.

მეოთხედის შუაში კოსინუსსა და სინუსს აქვთ ზუსტად იგივე მოდულის მნიშვნელობა: √2/2. რა შემთხვევაში ისინი პლიუს ან მინუს ნიშნით არიან - იხილეთ ცხრილი ზემოთ. მაგრამ თქვენ არ გჭირდებათ ასეთი ცხრილი: თქვენ ეს იცით იმავე მე-7 კლასის კურსიდან.

ყველა ყველაზე ახლოს ღერძთან Xწერტილებს აქვთ კოსინუსისა და სინუსის ზუსტად იგივე მოდულის მნიშვნელობები: (√3/2; 1/2).

ღერძთან ყველაზე ახლოს მყოფი მნიშვნელობები ზექულები ასევე აბსოლუტურად იდენტურია აბსოლუტური მნიშვნელობით - და მათ აქვთ იგივე რიცხვები, მხოლოდ მათ "გაცვალეს" ადგილები: (1/2; √3/2).

ახლა რაც შეეხება ნიშნებს - აქ არის საინტერესო მონაცვლეობა (თუმცა, მიგვაჩნია, რომ ნიშნები მაინც მარტივად უნდა გაიგოთ).

თუ პირველ კვარტალში როგორც კოსინუსის, ასევე სინუსის მნიშვნელობები არის პლუსის ნიშანი, მაშინ დიამეტრულად საპირისპირო (მესამე) ისინი მინუს ნიშნით არიან.

თუ მეორე მეოთხედში მინუს ნიშნით არის მხოლოდ კოსინუსები, მაშინ დიამეტრულად საპირისპირო (მეოთხეში) - მხოლოდ სინუსები.

რჩება მხოლოდ გავიხსენოთ, რომ კოსინუსის და სინუსების მნიშვნელობების თითოეულ კომბინაციაში პირველი რიცხვი არის კოსინუს მნიშვნელობა, მეორე რიცხვი არის სინუს მნიშვნელობა.

ყურადღება მიაქციეთ კიდევ ერთ კანონზომიერებას: წრის ყველა დიამეტრალურად საპირისპირო წერტილის სინუსი და კოსინუსი აბსოლუტური მნიშვნელობით აბსოლუტურად ტოლია. ავიღოთ, მაგალითად, საპირისპირო წერტილები π/3 და 4π/3:

cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2

ორი საპირისპირო წერტილის კოსინუსებისა და სინუსების მნიშვნელობები განსხვავდება მხოლოდ ნიშნით. მაგრამ აქაც არის ნიმუში: დიამეტრულად საპირისპირო წერტილების სინუსებსა და კოსინუსებს ყოველთვის აქვთ საპირისპირო ნიშნები.

მნიშვნელოვანია იცოდეთ:

რიცხვითი წრის წერტილების კოსინუსების და სინუსების მნიშვნელობები იზრდება ან მცირდება თანმიმდევრობით მკაცრად განსაზღვრული თანმიმდევრობით: უმცირესი მნიშვნელობიდან უდიდესამდე და პირიქით (იხ. განყოფილება "ტრიგონომეტრიული ფუნქციების გაზრდა და შემცირება" - თუმცა , ამის გადამოწმება მარტივია მხოლოდ ზემოთ მოცემული რიცხვების წრის დათვალიერებით).

კლებადობით, მიიღება მნიშვნელობების შემდეგი მონაცვლეობა:

√3 √2 1 1 √2 √3
1; --; --; -; 0; – -; – --; – --; –1
2 2 2 2 2 2

ისინი იზრდებიან ზუსტად საპირისპირო თანმიმდევრობით.

ამ მარტივი ნიმუშის გაგების შემდეგ, თქვენ შეისწავლით თუ როგორ უნდა განსაზღვროთ სინუსის და კოსინუსის მნიშვნელობები საკმაოდ მარტივად.

მარტივად რომ ვთქვათ, ეს არის წყალში მოხარშული ბოსტნეული სპეციალური რეცეპტის მიხედვით. განვიხილავ ორ საწყის კომპონენტს (ბოსტნეულის სალათს და წყალს) და დასრულებულ შედეგს - ბორშს. გეომეტრიულად, ეს შეიძლება იყოს წარმოდგენილი მართკუთხედის სახით, რომელშიც ერთი მხარე აღნიშნავს სალათის ფოთოლს, მეორე მხარე აღნიშნავს წყალს. ამ ორი მხარის ჯამი აღნიშნავს ბორშს. ასეთი "ბორშის" მართკუთხედის დიაგონალი და ფართობი არის წმინდა მათემატიკური ცნებები და არასოდეს გამოიყენება ბორშის რეცეპტებში.

როგორ იქცევა სალათის ფოთოლი და წყალი მათემატიკურად ბორშად? როგორ შეიძლება ორი სეგმენტის ჯამი გადაიქცეს ტრიგონომეტრიად? ამის გასაგებად, ჩვენ გვჭირდება წრფივი კუთხის ფუნქციები.

მათემატიკის სახელმძღვანელოებში წრფივი კუთხის ფუნქციების შესახებ ვერაფერს იპოვით. მაგრამ მათ გარეშე არ შეიძლება მათემატიკა. მათემატიკის კანონები, ისევე როგორც ბუნების კანონები, მუშაობს იმისდა მიუხედავად, ვიცით თუ არა მათი არსებობა.

წრფივი კუთხოვანი ფუნქციები არის მიმატების კანონები.ნახეთ, როგორ იქცევა ალგებრა გეომეტრიად და გეომეტრია ტრიგონომეტრიად.

შესაძლებელია თუ არა ხაზოვანი კუთხოვანი ფუნქციების გარეშე? შეგიძლია, რადგან მათემატიკოსები მაინც ახერხებენ მათ გარეშე. მათემატიკოსების ხრიკი მდგომარეობს იმაში, რომ ისინი ყოველთვის გვეუბნებიან მხოლოდ იმ ამოცანების შესახებ, რომელთა გადაჭრაც თავად შეუძლიათ და არასოდეს გვეუბნებიან იმ ამოცანების შესახებ, რომელთა გადაჭრაც მათ არ შეუძლიათ. იხ. თუ ვიცით შეკრების შედეგი და ერთი წევრი, გამოკლებას ვიყენებთ მეორე წევრის საპოვნელად. ყველაფერი. სხვა პრობლემები არ ვიცით და ვერც გადავჭრით. რა უნდა გავაკეთოთ, თუ ვიცით მხოლოდ მიმატების შედეგი და არ ვიცით ორივე ტერმინი? ამ შემთხვევაში, მიმატების შედეგი უნდა დაიშალოს ორ ტერმინად წრფივი კუთხოვანი ფუნქციების გამოყენებით. გარდა ამისა, ჩვენ თვითონ ვირჩევთ რა შეიძლება იყოს ერთი ტერმინი და წრფივი კუთხური ფუნქციები გვიჩვენებს რა უნდა იყოს მეორე წევრი, რათა მიმატების შედეგი იყოს ზუსტად ის, რაც გვჭირდება. ასეთი წყვილი ტერმინების უსასრულო რაოდენობა შეიძლება იყოს. ყოველდღიურ ცხოვრებაში ჩვენ ძალიან კარგად ვაკეთებთ ჯამის დაშლის გარეშე, გამოკლება საკმარისია ჩვენთვის. მაგრამ ბუნების კანონების მეცნიერულ კვლევებში ჯამის ტერმინებად გაფართოება შეიძლება ძალიან სასარგებლო იყოს.

დამატების კიდევ ერთი კანონი, რომელზედაც მათემატიკოსებს არ უყვართ ლაპარაკი (კიდევ ერთი მათი ხრიკი) მოითხოვს, რომ ტერმინებს ჰქონდეს იგივე საზომი ერთეული. სალათის ფურცლისთვის, წყლისა და ბორშისთვის ეს შეიძლება იყოს წონის, მოცულობის, ღირებულების ან გაზომვის ერთეული.

ნახაზი გვიჩვენებს მათემატიკის განსხვავების ორ დონეს. პირველი დონე არის განსხვავებები რიცხვების ველში, რომლებიც მითითებულია ა, ბ, გ. ამას აკეთებენ მათემატიკოსები. მეორე დონე არის განსხვავებები საზომი ერთეულების ფართობში, რომლებიც ნაჩვენებია კვადრატულ ფრჩხილებში და მითითებულია ასოებით. U. ამას აკეთებენ ფიზიკოსები. ჩვენ შეგვიძლია გავიგოთ მესამე დონე - განსხვავებები აღწერილი ობიექტების ფარგლებს შორის. სხვადასხვა ობიექტს შეიძლება ჰქონდეს ერთი და იგივე ზომის ერთეულების ერთი და იგივე რაოდენობა. რამდენად მნიშვნელოვანია ეს, შეგვიძლია დავინახოთ ბორშის ტრიგონომეტრიის მაგალითზე. თუ ერთსა და იმავე აღნიშვნას დავამატებთ სხვადასხვა ობიექტის გაზომვის ერთეულებს, შეგვიძლია ზუსტად ვთქვათ, რა მათემატიკური სიდიდე აღწერს კონკრეტულ ობიექტს და როგორ იცვლება ის დროთა განმავლობაში ან ჩვენს მოქმედებებთან დაკავშირებით. წერილი ვწყალს ასოთი მოვნიშნავ სსალათს ასოთი მოვნიშნავ ბ- ბორში. აი, როგორი იქნება ბორშჩის წრფივი კუთხის ფუნქციები.

წყლის ნაწილს და სალათის ნაწილს თუ ავიღებთ, ისინი ერთად გადაიქცევიან ბორშის ერთ პორციაში. აქვე გირჩევთ, ცოტათი დაისვენოთ ბორშჩისგან და გაიხსენოთ თქვენი შორეული ბავშვობა. გახსოვთ, როგორ გვასწავლეს კურდღლებისა და იხვების შეკრება? საჭირო იყო იმის დადგენა, რამდენი ცხოველი გამოვა. მერე რა გვასწავლეს? გვასწავლეს რიცხვებისგან ერთეულების გამოყოფა და რიცხვების შეკრება. დიახ, ნებისმიერი რიცხვი შეიძლება დაემატოს ნებისმიერ სხვა ნომერს. ეს არის პირდაპირი გზა თანამედროვე მათემატიკის აუტიზმისკენ - ჩვენ არ გვესმის რა, გაუგებარია რატომ და ძალიან ცუდად გვესმის, როგორ უკავშირდება ეს რეალობას, რადგან სამი დონის განსხვავების გამო, მათემატიკოსები მუშაობენ მხოლოდ ერთზე. უფრო სწორი იქნება ვისწავლოთ როგორ გადავიდეთ ერთი საზომი ერთეულიდან მეორეზე.

და კურდღლები, იხვები და პატარა ცხოველები შეიძლება დაითვალოს ნაჭრებად. ერთი საერთო საზომი ერთეული სხვადასხვა ობიექტებისთვის საშუალებას გვაძლევს დავამატოთ ისინი. ეს არის პრობლემის საბავშვო ვერსია. მოდით შევხედოთ მსგავს პრობლემას მოზრდილებში. რას იღებთ, როდესაც კურდღლებს და ფულს დაამატებთ? აქ ორი შესაძლო გამოსავალია.

პირველი ვარიანტი. ჩვენ განვსაზღვრავთ კურდღლების საბაზრო ღირებულებას და ვამატებთ მას ხელმისაწვდომ ნაღდ ფულს. ჩვენ მივიღეთ ჩვენი სიმდიდრის მთლიანი ღირებულება ფულის თვალსაზრისით.

მეორე ვარიანტი. თქვენ შეგიძლიათ დაამატოთ კურდღლების რაოდენობა ბანკნოტების რაოდენობას, რაც გვაქვს. მოძრავი ქონების რაოდენობას ნაწილებად მივიღებთ.

როგორც ხედავთ, იგივე დამატების კანონი საშუალებას გაძლევთ მიიღოთ განსხვავებული შედეგები. ეს ყველაფერი დამოკიდებულია იმაზე, თუ რა გვინდა ვიცოდეთ.

მაგრამ დავუბრუნდეთ ჩვენს ბორშს. ახლა ჩვენ ვხედავთ რა მოხდება ხაზოვანი კუთხის ფუნქციების კუთხის სხვადასხვა მნიშვნელობებისთვის.

კუთხე არის ნული. სალათი გვაქვს, მაგრამ წყალი არა. ბორშს ვერ ვამზადებთ. ბორშის რაოდენობაც ნულის ტოლია. ეს საერთოდ არ ნიშნავს იმას, რომ ნულოვანი ბორში უდრის ნულ წყალს. ნულოვანი ბორში ასევე შეიძლება იყოს ნულოვანი სალათი (მარჯვენა კუთხე).

პირადად ჩემთვის ეს არის მთავარი მათემატიკური დასტური იმისა, რომ . ნული არ ცვლის რიცხვს დამატებისას. ეს იმიტომ ხდება, რომ თავად დამატება შეუძლებელია, თუ არის მხოლოდ ერთი ტერმინი და აკლია მეორე წევრი. თქვენ შეგიძლიათ დაუკავშირდეთ ამას, როგორც გინდათ, მაგრამ გახსოვდეთ - ყველა მათემატიკური ოპერაცია ნულთან ერთად მათემატიკოსებმა გამოიგონეს, ასე რომ, გააუქმეთ თქვენი ლოგიკა და სულელურად შეავსეთ მათემატიკოსების მიერ გამოგონილი განმარტებები: "ნულზე გაყოფა შეუძლებელია", "ნებისმიერი რიცხვი გამრავლებული ნულზე". უდრის ნულს", "ნულ წერტილს მიღმა" და სხვა სისულელეებს. საკმარისია ერთხელ დაიმახსოვროთ, რომ ნული რიცხვი არ არის და არასოდეს გაგიჩნდებათ კითხვა, ნული ნატურალური რიცხვია თუ არა, რადგან ასეთი კითხვა საერთოდ კარგავს ყოველგვარ მნიშვნელობას: როგორ შეიძლება ჩაითვალოს რიცხვი, რომელიც არ არის რიცხვი. . ეს ჰგავს კითხვას, რა ფერს მივაკუთვნოთ უხილავი ფერი. რიცხვისთვის ნულის დამატება არარსებული საღებავით ხატვას ჰგავს. მშრალ ფუნჯს აფრიალებენ და ყველას ეუბნებიან, რომ „მოვხატეთ“. მაგრამ ცოტას ვშორდები.

კუთხე არის ნულზე მეტი, მაგრამ ორმოცდახუთი გრადუსზე ნაკლები. სალათის ფოთოლი ბევრი გვაქვს, წყალი კი ცოტა. შედეგად ვიღებთ სქელ ბორშს.

კუთხე ორმოცდახუთი გრადუსია. თანაბარი რაოდენობით გვაქვს წყალი და სალათის ფოთოლი. ეს შესანიშნავი ბორშია (მაპატიონ მზარეულებმა, ეს უბრალოდ მათემატიკაა).

კუთხე ორმოცდახუთი გრადუსზე მეტია, მაგრამ ოთხმოცდაათ გრადუსზე ნაკლები. ბევრი წყალი გვაქვს და ცოტა სალათი. მიიღეთ თხევადი ბორში.

მართი კუთხე. წყალი გვაქვს. სალათის ფოთოლზე მხოლოდ მოგონებები რჩება, რადგან ჩვენ ვაგრძელებთ კუთხის გაზომვას იმ ხაზიდან, რომელიც ოდესღაც სალათის ფოთლებს აღნიშნავდა. ბორშს ვერ ვამზადებთ. ბორშის რაოდენობა ნულის ტოლია. ამ შემთხვევაში დაიჭირეთ და დალიეთ წყალი სანამ ის ხელმისაწვდომია)))

Აქ. Რაღაც მსგავსი. აქ შემიძლია სხვა ისტორიების მოყოლა, რაც აქ უფრო შესაფერისი იქნება.

ორ მეგობარს საერთო საქმეში წილი ჰქონდათ. ერთი მათგანის მკვლელობის შემდეგ ყველაფერი მეორეზე გადავიდა.

მათემატიკის გაჩენა ჩვენს პლანეტაზე.

ყველა ეს ამბავი მოთხრობილია მათემატიკის ენაზე წრფივი კუთხოვანი ფუნქციების გამოყენებით. სხვა დროს მე გაჩვენებთ ამ ფუნქციების რეალურ ადგილს მათემატიკის სტრუქტურაში. ამასობაში, დავუბრუნდეთ ბორშის ტრიგონომეტრიას და განვიხილოთ პროგნოზები.

შაბათი, 2019 წლის 26 ოქტომბერი

მე ვუყურე საინტერესო ვიდეოს შესახებ გრანდის რიგი ერთს მინუს ერთი პლუს ერთი მინუს ერთი - Numberphile. მათემატიკოსები იტყუებიან. მათ არ ჩაატარეს თანასწორობის ტესტი მსჯელობაში.

ეს ეხმიანება ჩემს მსჯელობას.

მოდით უფრო დეტალურად განვიხილოთ ნიშნები, რომ მათემატიკოსები გვატყუებენ. მსჯელობის დასაწყისშივე მათემატიკოსები ამბობენ, რომ მიმდევრობის ჯამი დამოკიდებულია მასში ელემენტების რაოდენობა ლუწი თუ არა. ეს არის ობიექტურად დადასტურებული ფაქტი. Შემდეგ რა მოხდება?

შემდეგ მათემატიკოსები აკლებენ თანმიმდევრობას ერთიანობას. რას იწვევს ეს? ეს იწვევს თანმიმდევრობის ელემენტების რაოდენობის ცვლილებას - ლუწი რიცხვი იცვლება კენტ რიცხვში, კენტი რიცხვი იცვლება ლუწ რიცხვში. ბოლოს და ბოლოს, ჩვენ დავამატეთ ერთი ელემენტის ტოლი თანმიმდევრობით. მიუხედავად ყველა გარეგანი მსგავსებისა, ტრანსფორმაციის წინ თანმიმდევრობა არ არის გარდაქმნის შემდგომ მიმდევრობის ტოლი. მაშინაც კი, თუ ჩვენ ვსაუბრობთ უსასრულო მიმდევრობაზე, უნდა გვახსოვდეს, რომ უსასრულო მიმდევრობა კენტი რაოდენობის ელემენტებით არ არის უსასრულო მიმდევრობის ტოლი ელემენტების ლუწი რაოდენობით.

ელემენტების რაოდენობის მიხედვით განსხვავებულ ორ მიმდევრობას შორის ტოლობის ნიშნის დაყენებით, მათემატიკოსები ამტკიცებენ, რომ თანმიმდევრობის ჯამი არ არის დამოკიდებული მიმდევრობის ელემენტების რაოდენობაზე, რაც ეწინააღმდეგება ობიექტურად დადგენილ ფაქტს. შემდგომი მსჯელობა უსასრულო მიმდევრობის ჯამის შესახებ მცდარია, რადგან ის დაფუძნებულია ცრუ თანასწორობაზე.

თუ ხედავთ, რომ მათემატიკოსები მტკიცებულებების მსვლელობისას ათავსებენ ფრჩხილებს, გადააწყობენ მათემატიკური გამოთქმის ელემენტებს, დაამატებენ ან ამოიღებენ რაღაცას, იყავით ძალიან ფრთხილად, დიდი ალბათობით ისინი თქვენს მოტყუებას ცდილობენ. ბარათების შემთხვევის მსგავსად, მათემატიკოსები თქვენს ყურადღებას აქცევენ გამოხატვის სხვადასხვა მანიპულაციებით, რათა საბოლოოდ მოგცეთ ცრუ შედეგი. თუ თქვენ არ შეგიძლიათ გაიმეოროთ ბარათის ხრიკი მოტყუების საიდუმლოების ცოდნის გარეშე, მაშინ მათემატიკაში ყველაფერი ბევრად უფრო მარტივია: თქვენ არც კი გეპარებათ ეჭვი მოტყუებაზე, მაგრამ ყველა მანიპულაციის გამეორება მათემატიკური გამოთქმით საშუალებას გაძლევთ დაარწმუნოთ სხვები. შედეგის სისწორე, ისევე როგორც მაშინ, როცა დაგარწმუნეთ.

კითხვა აუდიტორიისგან: და უსასრულობა (როგორც ელემენტების რაოდენობა S მიმდევრობაში), არის ის ლუწი თუ კენტი? როგორ შეგიძლიათ შეცვალოთ პარიტეტი იმის, რასაც არ აქვს პარიტეტი?

მათემატიკოსებისთვის უსასრულობა მღვდლებისთვის ზეცის სამეფოს ჰგავს - იქ არავინ ყოფილა, მაგრამ ყველამ ზუსტად იცის, როგორ მუშაობს იქ ყველაფერი))) გეთანხმები, სიკვდილის შემდეგ აბსოლუტურად გულგრილი იქნები, იცხოვრე ლუწი თუ კენტი დღეები. , მაგრამ ... თქვენი ცხოვრების დასაწყისში მხოლოდ ერთ დღეს დავამატებთ, მივიღებთ სრულიად განსხვავებულ ადამიანს: მისი გვარი, სახელი და პატრონიმი ზუსტად იგივეა, მხოლოდ დაბადების თარიღი არის სრულიად განსხვავებული - ის დაიბადა ერთი. შენს წინ დღით.

ახლა კი საქმეზე))) დავუშვათ, სასრული მიმდევრობა, რომელსაც აქვს პარიტეტი, კარგავს ამ პარიტეტს უსასრულობამდე გადასვლისას. მაშინ უსასრულო მიმდევრობის ნებისმიერმა სასრულმა სეგმენტმა ასევე უნდა დაკარგოს პარიტეტი. ჩვენ ამას არ ვაკვირდებით. ის ფაქტი, რომ დანამდვილებით ვერ ვიტყვით, ელემენტების რაოდენობა უსასრულო მიმდევრობაში ლუწია თუ კენტი, საერთოდ არ ნიშნავს, რომ პარიტეტი გაქრა. პარიტეტი, თუ ის არსებობს, უკვალოდ ვერ გაქრება უსასრულობაში, როგორც კარტის ბასრი ყდის. ამ საქმის ძალიან კარგი ანალოგია.

ოდესმე გკითხავთ საათში მჯდომ გუგულს, რომელი მიმართულებით ბრუნავს საათის ისარი? მისთვის ისარი ბრუნავს საპირისპირო მიმართულებით, რასაც ჩვენ ვუწოდებთ "საათის ისრის". შეიძლება პარადოქსულად ჟღერდეს, მაგრამ ბრუნის მიმართულება დამოკიდებულია მხოლოდ იმაზე, თუ რომელი მხრიდან ვაკვირდებით ბრუნვას. ასე რომ, ჩვენ გვაქვს ერთი ბორბალი, რომელიც ბრუნავს. ვერ ვიტყვით, რა მიმართულებით ხდება ბრუნვა, რადგან შეგვიძლია დავაკვირდეთ მას როგორც ბრუნის სიბრტყის ერთი მხრიდან, ასევე მეორე მხრიდან. ჩვენ მხოლოდ იმის მოწმობა შეგვიძლია, რომ არსებობს როტაცია. სრული ანალოგია უსასრულო მიმდევრობის პარიტეტთან ს.

ახლა დავამატოთ მეორე მბრუნავი ბორბალი, რომლის ბრუნვის სიბრტყე პარალელურია პირველი მბრუნავი ბორბლის ბრუნვის სიბრტყის. ჩვენ ჯერ კიდევ არ შეგვიძლია ზუსტად გეტყვით, რომელი მიმართულებით ტრიალებს ეს ბორბლები, მაგრამ ჩვენ შეგვიძლია აბსოლუტური დარწმუნებით ვთქვათ, ორივე ბორბალი ტრიალებს იმავე მიმართულებით თუ საპირისპირო მიმართულებით. ორი უსასრულო მიმდევრობის შედარება სდა 1-ს, მათემატიკის დახმარებით ვაჩვენე, რომ ამ მიმდევრობებს განსხვავებული პარიტეტი აქვთ და მათ შორის ტოლობის ნიშნის დადება შეცდომაა. პირადად მე მჯერა მათემატიკის, არ ვენდობი მათემატიკოსებს))) სხვათა შორის, იმისთვის, რომ სრულად გავიგოთ უსასრულო მიმდევრობების გარდაქმნების გეომეტრია, აუცილებელია კონცეფციის შემოღება. "ერთდროულობა". ამის დახატვა დასჭირდება.

ოთხშაბათი, 7 აგვისტო, 2019 წ

საუბრის დასრულებისას ჩვენ უნდა განვიხილოთ უსასრულო ნაკრები. იმის გათვალისწინებით, რომ "უსასრულობის" კონცეფცია მოქმედებს მათემატიკოსებზე, როგორც ბოა კონსტრიქტორი კურდღელზე. უსასრულობის მომაჯადოებელი საშინელება მათემატიკოსებს ართმევს საღ აზრს. აი მაგალითი:

ორიგინალური წყარო მდებარეობს. ალფა აღნიშნავს ნამდვილ რიცხვს. ზემოთ მოცემულ გამონათქვამებში ტოლობის ნიშანი მიუთითებს იმაზე, რომ თუ უსასრულობას დაუმატებთ რიცხვს ან უსასრულობას, არაფერი შეიცვლება, შედეგი იქნება იგივე უსასრულობა. თუ მაგალითისთვის ავიღებთ ნატურალური რიცხვების უსასრულო სიმრავლეს, მაშინ განხილული მაგალითები შეიძლება წარმოვიდგინოთ შემდეგნაირად:

მათი საქმის ვიზუალურად დასამტკიცებლად მათემატიკოსებმა მრავალი განსხვავებული მეთოდი მოიგონეს. მე პირადად ყველა ამ მეთოდს ვუყურებ, როგორც შამანების ცეკვას ტამბურთან. არსებითად, ისინი ყველა ჩამოდიან იმ ფაქტზე, რომ ან ზოგიერთი ოთახი დაკავებული არ არის და მათში ახალი სტუმრები სახლდებიან, ან ზოგიერთ სტუმარს დერეფანში აგდებენ სტუმრებისთვის ადგილის გასათავისუფლებლად (ძალიან ადამიანურად). მე წარმოვადგინე ჩემი შეხედულება ასეთ გადაწყვეტილებებზე ფანტასტიკური ისტორიის სახით ქერაზე. რას ეფუძნება ჩემი მსჯელობა? უსასრულო რაოდენობის ვიზიტორთა გადაადგილებას უსასრულო დრო სჭირდება. მას შემდეგ, რაც ჩვენ გავათავისუფლებთ პირველ სასტუმრო ოთახს, ერთ-ერთი სტუმარი ყოველთვის გადის დერეფნის გასწვრივ თავისი ოთახიდან მეორე ოთახში დროის ბოლომდე. რა თქმა უნდა, დროის ფაქტორის უგულებელყოფა შეიძლება სულელურად, მაგრამ ეს უკვე კატეგორიიდან იქნება „კანონი სულელებისთვის არ წერია“. ეს ყველაფერი დამოკიდებულია იმაზე, თუ რას ვაკეთებთ: რეალობის მორგება მათემატიკურ თეორიებზე ან პირიქით.

რა არის "უსასრულო სასტუმრო"? Infinity Inn არის სასტუმრო, რომელსაც ყოველთვის აქვს ნებისმიერი რაოდენობის ვაკანსია, რამდენი ოთახიც არ უნდა იყოს დაკავებული. თუ გაუთავებელ დერეფანში „ვიზიტორებისთვის“ ყველა ოთახი დაკავებულია, არის კიდევ ერთი გაუთავებელი დერეფანი „სტუმრებისთვის“ ოთახებით. ასეთი დერეფნების უსასრულო რაოდენობა იქნება. ამავდროულად, „უსასრულო სასტუმროს“ აქვს უსასრულო რაოდენობის სართულები უსასრულო რაოდენობის შენობებში უსასრულო რაოდენობის პლანეტებზე უსასრულო რაოდენობის ღმერთების მიერ შექმნილ სამყაროებში. მათემატიკოსები კი ბანალურ ყოველდღიურ პრობლემებს ვერ შორდებიან: ღმერთი-ალაჰ-ბუდა ყოველთვის ერთია, სასტუმრო ერთია, დერეფანი მხოლოდ ერთი. ასე რომ, მათემატიკოსები ცდილობენ სასტუმროს ნომრების სერიული ნომრების ჟონგლირებას, დაგვარწმუნონ იმაში, რომ შესაძლებელია „გაუძარცველის გადაყრა“.

მე გაჩვენებთ ჩემი მსჯელობის ლოგიკას ნატურალური რიცხვების უსასრულო სიმრავლის მაგალითის გამოყენებით. ჯერ უნდა უპასუხოთ ძალიან მარტივ კითხვას: ნატურალური რიცხვების რამდენი სიმრავლე არსებობს - ერთი თუ ბევრი? ამ კითხვაზე სწორი პასუხი არ არსებობს, რადგან ჩვენ თვითონ გამოვიგონეთ რიცხვები, ბუნებაში რიცხვები არ არსებობს. დიახ, ბუნებამ მშვენივრად იცის დათვლა, მაგრამ ამისთვის იყენებს სხვა მათემატიკურ საშუალებებს, რომლებიც ჩვენთვის არ არის ნაცნობი. როგორც ბუნება ფიქრობს, სხვა დროს გეტყვით. ვინაიდან ჩვენ გამოვიგონეთ რიცხვები, ჩვენ თვითონ გადავწყვეტთ ნატურალური რიცხვების რამდენი კომპლექტი არსებობს. განიხილეთ ორივე ვარიანტი, როგორც ეს შეეფერება ნამდვილ მეცნიერს.

ვარიანტი ერთი. „მოდით მოგვცეს“ ნატურალური რიცხვების ერთი ნაკრები, რომელიც მშვიდად დევს თაროზე. ამ კომპლექტს თაროდან ვიღებთ. ესე იგი, თაროზე სხვა ნატურალური რიცხვები აღარ დარჩა და წასაღებიც არსად არის. ჩვენ ვერ დავამატებთ ამ კომპლექტს, რადგან უკვე გვაქვს. რა მოხდება, თუ მართლა გინდა? Არაა პრობლემა. ჩვენ შეგვიძლია ავიღოთ ერთეული უკვე აღებული ნაკრებიდან და დავაბრუნოთ თაროზე. ამის შემდეგ შეგვიძლია თაროდან ავიღოთ ერთეული და დავამატოთ ის რაც დაგვრჩა. შედეგად, ჩვენ კვლავ ვიღებთ ნატურალური რიცხვების უსასრულო სიმრავლეს. თქვენ შეგიძლიათ დაწეროთ ყველა ჩვენი მანიპულაცია ასე:

ჩავწერე მოქმედებები ალგებრული აღნიშვნით და სიმრავლეების თეორიის აღნიშვნით, სიმრავლის ელემენტები დეტალურად ჩამოვთვალე. სუბსკრიპტი მიუთითებს, რომ ჩვენ გვაქვს ნატურალური რიცხვების ერთი და ერთადერთი ნაკრები. გამოდის, რომ ნატურალური რიცხვების სიმრავლე უცვლელი დარჩება მხოლოდ იმ შემთხვევაში, თუ მას ერთი გამოაკლდება და იგივე დაემატება.

ვარიანტი ორი. თაროზე გვაქვს ბუნებრივი რიცხვების მრავალი განსხვავებული უსასრულო ნაკრები. ხაზს ვუსვამ - განსხვავებულს, მიუხედავად იმისა, რომ ისინი პრაქტიკულად არ განსხვავდებიან. ჩვენ ვიღებთ ერთ-ერთ ამ კომპლექტს. შემდეგ ვიღებთ ერთს ნატურალური რიცხვების მეორე სიმრავლიდან და ვამატებთ უკვე აღებულ სიმრავლეს. შეგვიძლია ნატურალური რიცხვების ორი კომპლექტიც კი დავამატოთ. აი რას მივიღებთ:

ხელმოწერები "ერთი" და "ორი" მიუთითებს იმაზე, რომ ეს ელემენტები განსხვავებულ კომპლექტს ეკუთვნოდა. დიახ, თუ ერთს დაუმატებთ უსასრულო კომპლექტს, შედეგი ასევე იქნება უსასრულო ნაკრები, მაგრამ ის არ იქნება იგივე, რაც ორიგინალური ნაკრები. თუ ერთ უსასრულო სიმრავლეს დაემატება კიდევ ერთი უსასრულო სიმრავლე, შედეგი არის ახალი უსასრულო სიმრავლე, რომელიც შედგება პირველი ორი სიმრავლის ელემენტებისაგან.

ნატურალური რიცხვების სიმრავლე გამოიყენება დასათვლელად ისევე, როგორც საზომი სახაზავი. ახლა წარმოიდგინეთ, რომ სახაზავს ერთი სანტიმეტრი დაუმატეთ. ეს უკვე განსხვავებული ხაზი იქნება, ორიგინალის ტოლი არ არის.

შეგიძლიათ მიიღოთ ან არ მიიღოთ ჩემი მსჯელობა - ეს თქვენი საქმეა. მაგრამ თუ ოდესმე მათემატიკურ პრობლემებს წააწყდებით, დაფიქრდით, დგახართ თუ არა ცრუ მსჯელობის გზაზე, რომელსაც მათემატიკოსთა თაობა არღვევს. მათემატიკის გაკვეთილები ხომ, უპირველეს ყოვლისა, აყალიბებს ჩვენში აზროვნების სტაბილურ სტერეოტიპს და მხოლოდ ამის შემდეგ გვმატებენ გონებრივ შესაძლებლობებს (ან პირიქით, გვართმევენ თავისუფალ აზროვნებას).

pozg.ru

კვირა, 4 აგვისტო, 2019 წ

მე ვწერდი პოსტსკრიპტს სტატიის შესახებ და ვნახე ეს შესანიშნავი ტექსტი ვიკიპედიაში:

ჩვენ ვკითხულობთ: „...ბაბილონური მათემატიკის მდიდარ თეორიულ საფუძველს არ გააჩნდა ჰოლისტიკური ხასიათი და დაყვანილი იყო განსხვავებული ტექნიკის ერთობლიობამდე, მოკლებული საერთო სისტემისა და მტკიცებულების ბაზას“.

Ვაუ! რამდენად ჭკვიანები ვართ და რამდენად კარგად ვხედავთ სხვის ნაკლოვანებებს. ჩვენთვის სუსტია თანამედროვე მათემატიკის იმავე კონტექსტში შეხედვა? ზემოაღნიშნული ტექსტის ოდნავ პერიფრაზირებით, პირადად მე მივიღე შემდეგი:

თანამედროვე მათემატიკის მდიდარ თეორიულ საფუძველს არ აქვს ჰოლისტიკური ხასიათი და დაყვანილია განსხვავებული სექციების ერთობლიობამდე, მოკლებულია საერთო სისტემისა და მტკიცებულების ბაზას.

შორს არ წავალ ჩემი სიტყვების დასადასტურებლად – მას აქვს ენა და კონვენციები, რომლებიც განსხვავდება მათემატიკის მრავალი სხვა დარგის ენისა და კონვენციებისგან. მათემატიკის სხვადასხვა ფილიალში ერთსა და იმავე სახელს შეიძლება ჰქონდეს განსხვავებული მნიშვნელობა. მსურს პუბლიკაციების მთელი ციკლი მივუძღვნა თანამედროვე მათემატიკის ყველაზე აშკარა შეცდომებს. Მალე გნახავ.

შაბათი, 3 აგვისტო, 2019 წ

როგორ დავყოთ ნაკრები ქვეჯგუფებად? ამისათვის თქვენ უნდა შეიყვანოთ ახალი საზომი ერთეული, რომელიც წარმოდგენილია შერჩეული ნაკრების ზოგიერთ ელემენტში. განვიხილოთ მაგალითი.

შეიძლება ბევრი გვქონდეს მაგრამშედგება ოთხი ადამიანისგან. ეს ნაკრები იქმნება „ხალხის“ საფუძველზე. მოდით, ასოების მეშვეობით განვსაზღვროთ ამ ნაკრების ელემენტები ა, ნომრის მქონე ხელმოწერა მიუთითებს ამ ნაკრების თითოეული ადამიანის რიგით ნომერს. შემოვიტანოთ ახალი საზომი ერთეული „სექსუალური მახასიათებელი“ და აღვნიშნოთ ასოებით ბ. ვინაიდან სექსუალური მახასიათებლები ყველა ადამიანშია თანდაყოლილი, ჩვენ ვამრავლებთ ნაკრების თითოეულ ელემენტს მაგრამსქესზე ბ. გაითვალისწინეთ, რომ ჩვენი "ხალხის" ნაკრები ახლა გახდა "ხალხის სქესის" ნაკრები. ამის შემდეგ შეგვიძლია სექსუალური მახასიათებლები მამრობითად დავყოთ ბმდა ქალთა bwგენდერული მახასიათებლები. ახლა ჩვენ შეგვიძლია გამოვიყენოთ მათემატიკური ფილტრი: ჩვენ ვირჩევთ ერთ-ერთ ამ სექსუალურ მახასიათებელს, არ აქვს მნიშვნელობა რომელია მამაკაცი თუ ქალი. თუ ის ადამიანშია, მაშინ ვამრავლებთ ერთზე, თუ ასეთი ნიშანი არ არის, ვამრავლებთ ნულზე. შემდეგ ჩვენ ვიყენებთ ჩვეულებრივ სასკოლო მათემატიკას. ნახეთ რა მოხდა.

გამრავლების, შემცირებისა და გადაწყობის შემდეგ მივიღეთ ორი ქვესიმრავლე: მამრობითი ქვესიმრავლე ბმდა ქალების ქვეჯგუფი bw. დაახლოებით ისევე მსჯელობენ მათემატიკოსები, როდესაც ისინი იყენებენ სიმრავლეების თეორიას პრაქტიკაში. მაგრამ ისინი არ გვიშვებენ დეტალებში, არამედ გვაძლევენ დასრულებულ შედეგს – „ბევრი ადამიანი შედგება კაცების და ქალების ქვეჯგუფისაგან“. ბუნებრივია, შეიძლება გაგიჩნდეთ კითხვა, რამდენად სწორად გამოიყენება მათემატიკა ზემოთ ჩამოთვლილ გარდაქმნებში? გარწმუნებთ, რომ რეალურად გარდაქმნები ხდება სწორად, საკმარისია ვიცოდეთ არითმეტიკის, ლოგის ალგებრის და მათემატიკის სხვა მონაკვეთების მათემატიკური დასაბუთება. რა არის ეს? სხვა დროს გეტყვით ამის შესახებ.

რაც შეეხება სუპერკომპლექტებს, შესაძლებელია ორი კომპლექტის გაერთიანება ერთ სუპერკომპლექტში საზომი ერთეულის არჩევით, რომელიც იმყოფება ამ ორი ნაკრების ელემენტებში.

როგორც ხედავთ, საზომი ერთეულები და საერთო მათემატიკა სიმრავლეების თეორიას წარსულს აქცევს. იმის ნიშანი, რომ სიმრავლეების თეორიაში ყველაფერი კარგად არ არის, არის ის, რომ მათემატიკოსებმა გამოიგონეს საკუთარი ენა და ჩანაწერები სიმრავლეების თეორიისთვის. მათემატიკოსებმა გააკეთეს ის, რაც ერთხელ გააკეთეს შამანებმა. მხოლოდ შამანებმა იციან როგორ გამოიყენონ თავიანთი „ცოდნა“ „სწორად“. ამ "ცოდნას" ისინი გვასწავლიან.

დასასრულს, მინდა გაჩვენოთ, როგორ მანიპულირებენ მათემატიკოსები
ვთქვათ აქილევსი კუზე ათჯერ უფრო სწრაფად დარბის და ათასი ნაბიჯით ჩამორჩება. იმ დროში, რაც აქილევსს სჭირდება ამ მანძილის გასაშვებად, კუ ასი ნაბიჯით გაივლის იმავე მიმართულებით. როცა აქილევსი ას საფეხურს გაივლის, კუს კიდევ ათი ნაბიჯი დაცოცავს და ა.შ. პროცესი უსასრულოდ გაგრძელდება, აქილევსი კუს ვერასოდეს მიაღწევს.

ეს მსჯელობა ლოგიკური შოკი გახდა ყველა შემდგომი თაობისთვის. არისტოტელე, დიოგენე, კანტი, ჰეგელი, გილბერტი... ყველა მათგანი ასე თუ ისე ზენონის აპორიებს თვლიდა. შოკი იმდენად ძლიერი იყო, რომ " ... მსჯელობა ამჟამად გრძელდება, სამეცნიერო საზოგადოებას ჯერ არ მიუღწევია პარადოქსების არსის შესახებ საერთო მოსაზრებამდე... საკითხის შესწავლაში ჩართული იყო მათემატიკური ანალიზი, სიმრავლეების თეორია, ახალი ფიზიკური და ფილოსოფიური მიდგომები. ; არცერთი მათგანი არ გახდა პრობლემის საყოველთაოდ მიღებული გადაწყვეტა ..."[ვიკიპედია," ზენონის აპორია "]. ყველას ესმის, რომ ატყუებენ, მაგრამ არავის ესმის რა არის მოტყუება.

მათემატიკის თვალსაზრისით, ზენონმა თავის აპორიაში ნათლად აჩვენა გადასვლა მნიშვნელობიდან. ეს გადასვლა გულისხმობს გამოყენებას მუდმივების ნაცვლად. რამდენადაც მე მესმის, საზომი ცვლადი ერთეულების გამოყენების მათემატიკური აპარატი ან ჯერ არ არის შემუშავებული, ან არ არის გამოყენებული ზენონის აპორიაზე. ჩვენი ჩვეული ლოგიკის გამოყენება მახეში მიგვიყვანს. ჩვენ, აზროვნების ინერციით, ვიყენებთ დროის მუდმივ ერთეულებს ურთიერთსაწინააღმდეგოზე. ფიზიკური თვალსაზრისით, როგორც ჩანს, დრო ნელდება სრულ გაჩერებამდე იმ მომენტში, როდესაც აქილევსი კუს დაეწია. თუ დრო გაჩერდება, აქილევსი ვეღარ გაუსწრებს კუს.

თუ შევეჩვიეთ ლოგიკას, ყველაფერი თავის ადგილზე დგება. აქილევსი მუდმივი სიჩქარით დარბის. მისი გზის ყოველი მომდევნო სეგმენტი წინაზე ათჯერ მოკლეა. შესაბამისად, მის დაძლევაზე დახარჯული დრო წინაზე ათჯერ ნაკლებია. თუ ამ სიტუაციაში „უსასრულობის“ ცნებას გამოვიყენებთ, მაშინ სწორი იქნება ვთქვათ „აქილევსი უსაზღვროდ სწრაფად გაუსწრებს კუს“.

როგორ ავიცილოთ თავიდან ეს ლოგიკური ხაფანგი? დარჩით დროის მუდმივ ერთეულებში და არ გადახვიდეთ საპასუხო მნიშვნელობებზე. ზენონის ენაზე ასე გამოიყურება:

იმ დროს, რაც აქილევსს სჭირდება ათასი ნაბიჯის გასაშვებად, კუს ასი ნაბიჯის გადადგმა იმავე მიმართულებით. შემდეგი დროის ინტერვალის განმავლობაში, პირველის ტოლფასი, აქილევსი კიდევ ათას ნაბიჯს გაივლის, კუს კი ასი ნაბიჯით გაივლის. ახლა აქილევსი რვაასი ნაბიჯით უსწრებს კუს.

ეს მიდგომა ადეკვატურად აღწერს რეალობას ყოველგვარი ლოგიკური პარადოქსების გარეშე. მაგრამ ეს არ არის პრობლემის სრული გადაწყვეტა. აინშტაინის განცხადება სინათლის სიჩქარის დაუძლეველობის შესახებ ძალიან ჰგავს ზენონის აპორიას „აქილევსი და კუს“. ჩვენ ჯერ კიდევ უნდა შევისწავლოთ, გადავხედოთ და გადავჭრათ ეს პრობლემა. და გამოსავალი უნდა ვეძიოთ არა უსასრულოდ დიდი რაოდენობით, არამედ გაზომვის ერთეულებში.

ზენონის კიდევ ერთი საინტერესო აპორია მოგვითხრობს მფრინავი ისრის შესახებ:

მფრინავი ისარი უმოძრაოა, რადგან დროის ყოველ მომენტში ის ისვენებს, და რადგან ის ისვენებს დროის ყოველ მომენტში, ის ყოველთვის ისვენებს.

ამ აპორიაში ლოგიკური პარადოქსი დაძლეულია ძალიან მარტივად - საკმარისია იმის გარკვევა, რომ დროის ყოველ მომენტში მფრინავი ისარი ისვენებს სივრცის სხვადასხვა წერტილში, რაც, ფაქტობრივად, მოძრაობაა. აქ უნდა აღინიშნოს კიდევ ერთი წერტილი. გზაზე მანქანის ერთი ფოტოსურათიდან შეუძლებელია მისი გადაადგილების ფაქტის და მასამდე მანძილის დადგენა. მანქანის მოძრაობის ფაქტის დასადგენად საჭიროა ერთი და იმავე წერტილიდან დროის სხვადასხვა მომენტში გადაღებული ორი ფოტო, მაგრამ მათი გამოყენება მანძილის დასადგენად არ შეიძლება. მანქანამდე მანძილის დასადგენად, საჭიროა ერთდროულად ორი ფოტო გადაღებული სივრცეში სხვადასხვა წერტილიდან, მაგრამ მათგან მოძრაობის ფაქტს ვერ განსაზღვრავთ (ბუნებრივია, გამოთვლებისთვის მაინც გჭირდებათ დამატებითი მონაცემები, ტრიგონომეტრია დაგეხმარებათ). კონკრეტულად მინდა აღვნიშნო, რომ ორი წერტილი დროისა და ორი წერტილი სივრცეში არის ორი განსხვავებული რამ, რაც არ უნდა აგვერიოს, რადგან ისინი აძლევენ სხვადასხვა შესაძლებლობებს კვლევისთვის.
მე გაჩვენებთ პროცესს მაგალითით. ჩვენ ვირჩევთ "წითელ სოლიდს მუწუკში" - ეს არის ჩვენი "მთელი". ამავდროულად, ჩვენ ვხედავთ, რომ ეს ნივთები არის მშვილდით და არის მშვილდის გარეშე. ამის შემდეგ ვირჩევთ „მთლიანის“ ნაწილს და ვქმნით კომპლექტს „მშვილდით“. ასე იკვებებიან შამანები თავიანთი სიმრავლის თეორიის რეალობასთან მიბმის გზით.

ახლა მოდით გავაკეთოთ პატარა ხრიკი. ავიღოთ "მყარი მუწუკში მშვილდით" და გავაერთიანოთ ეს "მთლიანები" ფერის მიხედვით, შევარჩიოთ წითელი ელემენტები. ბევრი "წითელი" მივიღეთ. ახლა რთული კითხვა: მიღებული კომპლექტები "მშვილდით" და "წითელი" ერთი და იგივე ნაკრებია თუ ორი განსხვავებული კომპლექტი? პასუხი მხოლოდ შამანებმა იციან. უფრო ზუსტად, თვითონაც არაფერი იციან, მაგრამ როგორც ამბობენ, ასეც იყოს.

ეს მარტივი მაგალითი გვიჩვენებს, რომ სიმრავლეების თეორია სრულიად უსარგებლოა, როცა საქმე რეალობას ეხება. რა არის საიდუმლო? ჩვენ ჩამოვაყალიბეთ კომპლექტი "წითელი მყარი pimply ერთად მშვილდი". ფორმირება მოხდა ოთხი განსხვავებული საზომი ერთეულის მიხედვით: ფერი (წითელი), სიმტკიცე (მყარი), უხეშობა (მუწუკში), დეკორაციები (მშვილდით). მხოლოდ საზომი ერთეულების ნაკრები იძლევა რეალური ობიექტების ადეკვატურად აღწერას მათემატიკის ენაზე. აი, როგორ გამოიყურება.

ასო „ა“ სხვადასხვა ინდექსით აღნიშნავს სხვადასხვა საზომ ერთეულს. ფრჩხილებში ხაზგასმულია საზომი ერთეულები, რომლის მიხედვითაც წინასწარ ეტაპზე ნაწილდება „მთელი“. საზომი ერთეული, რომლის მიხედვითაც ყალიბდება ნაკრები, ამოღებულია ფრჩხილებიდან. ბოლო ხაზი აჩვენებს საბოლოო შედეგს - ნაკრების ელემენტს. როგორც ხედავთ, თუ ჩვენ ვიყენებთ ერთეულებს ნაკრების შესაქმნელად, მაშინ შედეგი არ არის დამოკიდებული ჩვენი მოქმედებების თანმიმდევრობაზე. და ეს მათემატიკაა და არა შამანების ცეკვები ტამბურით. შამანებს შეუძლიათ „ინტუიტიურად“ მივიდნენ იმავე შედეგამდე, ამტკიცებენ მას „აშკარად“, რადგან საზომი ერთეულები არ შედის მათ „მეცნიერულ“ არსენალში.

საზომი ერთეულების დახმარებით ძალიან ადვილია ერთის დაშლა ან რამდენიმე ნაკრების ერთ სუპერსეტში გაერთიანება. მოდით უფრო ახლოს მივხედოთ ამ პროცესის ალგებრას.

ტრიგონომეტრიული ფუნქციის ნიშანი დამოკიდებულია მხოლოდ კოორდინატთა მეოთხედზე, რომელშიც მდებარეობს რიცხვითი არგუმენტი. ბოლო დროს ვისწავლეთ, როგორ გადავთარგმნოთ არგუმენტები რადიანის საზომიდან ხარისხობრივ საზომად (იხილეთ გაკვეთილი „კუთხის რადიანი და გრადუსიანი საზომი“) და შემდეგ განვსაზღვროთ იგივე კოორდინატთა მეოთხედი. ახლა, ფაქტობრივად, შევეხოთ სინუსის, კოსინუსის და ტანგენტის ნიშნის განსაზღვრას.

α კუთხის სინუსი არის ტრიგონომეტრიული წრის წერტილის ორდინატი (კოორდინატი y), რომელიც ჩნდება, როდესაც რადიუსი ბრუნავს α კუთხით.

α კუთხის კოსინუსი არის ტრიგონომეტრიული წრის წერტილის აბსცისა (x კოორდინატი), რომელიც ჩნდება, როდესაც რადიუსი ბრუნავს α კუთხეში.

α კუთხის ტანგენსი არის სინუსის შეფარდება კოსინუსთან. ან, ექვივალენტურად, y-კოორდინატის შეფარდება x-კოორდინატთან.

აღნიშვნა: sin α = y ; cosα = x; tgα = y: x.

ყველა ეს განმარტება თქვენთვის ცნობილია უმაღლესი სკოლის ალგებრის კურსიდან. თუმცა, ჩვენ არ გვაინტერესებს თავად განსაზღვრებები, არამედ შედეგები, რომლებიც წარმოიქმნება ტრიგონომეტრიულ წრეზე. Შეხედე:

ლურჯი მიუთითებს OY ღერძის დადებით მიმართულებაზე (y-ღერძი), წითელი მიუთითებს OX ღერძის დადებით მიმართულებაზე (აბსციზა). ამ "რადარზე" აშკარა ხდება ტრიგონომეტრიული ფუნქციების ნიშნები. Კერძოდ:

1. sin α > 0 თუ კუთხე α დევს I ან II კოორდინატთა მეოთხედში. ეს იმიტომ ხდება, რომ, განსაზღვრებით, სინუსი არის ორდინატი (y კოორდინატი). ხოლო y კოორდინატი დადებითი იქნება ზუსტად I და II კოორდინატთა კვარტალებში;
2. cos α > 0 თუ კუთხე α დევს I ან IV კოორდინატთა მეოთხედში. რადგან მხოლოდ იქ x კოორდინატი (ის ასევე არის აბსციზა) იქნება ნულზე მეტი;
3. tg α > 0, თუ კუთხე α დევს I ან III კოორდინატულ კვადრატში. ეს გამომდინარეობს განმარტებიდან: ბოლოს და ბოლოს, tg α = y : x , ამიტომ დადებითია მხოლოდ იქ, სადაც x და y ნიშნები ემთხვევა ერთმანეთს. ეს ხდება 1 კოორდინატთა კვარტალში (აქ x > 0, y > 0) და მე-3 კოორდინატულ კვარტალში (x< 0, y < 0).

სიცხადისთვის ჩვენ აღვნიშნავთ თითოეული ტრიგონომეტრიული ფუნქციის ნიშნებს - სინუსს, კოსინუსს და ტანგენტს - ცალკეულ "რადაროზე". ჩვენ ვიღებთ შემდეგ სურათს:

შენიშვნა: ჩემს მსჯელობაში არასდროს მითქვამს მეოთხე ტრიგონომეტრიულ ფუნქციაზე - კოტანგენტს. ფაქტია, რომ კოტანგენსის ნიშნები ემთხვევა ტანგენსის ნიშნებს - იქ განსაკუთრებული წესები არ არსებობს.

ახლა მე ვთავაზობ B11 პრობლემების მსგავსი მაგალითების განხილვას საცდელი გამოცდამათემატიკაში, რომელიც შედგა 2011 წლის 27 სექტემბერს. ბოლოს და ბოლოს Საუკეთესო გზათეორიის გაგება პრაქტიკაა. სასურველია ბევრი პრაქტიკა. რა თქმა უნდა, დავალებების პირობები ოდნავ შეიცვალა.

Დავალება. განსაზღვრეთ ტრიგონომეტრიული ფუნქციების და გამონათქვამების ნიშნები (თვით ფუნქციების მნიშვნელობების გათვალისწინება არ არის საჭირო):

1. sin (3π/4);
2. cos(7π/6);
3. რუჯი (5π/3);
4. sin(3π/4) cos(5π/6);
5. cos (2π/3) tg (π/4);
6. sin(5π/6) cos(7π/4);
7. რუჯი (3π/4) cos (5π/3);
8. ctg (4π/3) tg (π/6).

სამოქმედო გეგმა ასეთია: ჯერ ყველა კუთხეს რადიანის საზომიდან გადავიყვანთ გრადუსულ ზომაზე (π → 180°), შემდეგ კი ვნახოთ, რომელ კოორდინატთა მეოთხედში დევს მიღებული რიცხვი. კვარტლების ცოდნით, ჩვენ მარტივად შეგვიძლია ვიპოვოთ ნიშნები - ახლახან აღწერილი წესების მიხედვით. Ჩვენ გვაქვს:

1. ცოდვა (3π/4) = ცოდვა (3 180°/4) = ცოდვა 135°. ვინაიდან 135° ∈ , ეს არის კუთხე II კოორდინატთა კვადრატიდან. მაგრამ მეორე მეოთხედში სინუსი დადებითია, ამიტომ sin (3π/4) > 0;
2. cos (7π/6) = cos (7 180°/6) = cos 210°. იმიტომ რომ 210° ∈, ეს არის კუთხე III კოორდინატთა კვადრატიდან, რომელშიც ყველა კოსინუსი უარყოფითია. ამიტომ, cos (7π/6)< 0;
3. tg (5π/3) = tg (5 180°/3) = tg 300°. 300° ∈ , ჩვენ ვართ IV კვადრატში, სადაც ტანგენსი უარყოფით მნიშვნელობებს იღებს. ამიტომ tg (5π/3)< 0;
4. sin (3π/4) cos (5π/6) = sin (3 180°/4) cos (5 180°/6) = sin 135° cos 150°. გავუმკლავდეთ სინუსს: იმიტომ 135° ∈ , ეს არის მეორე მეოთხედი, რომელშიც სინუსები დადებითია, ე.ი. sin (3π/4) > 0. ახლა ვმუშაობთ კოსინუსთან: 150° ∈ - ისევ მეორე მეოთხედი, იქ კოსინუსები უარყოფითია. ამიტომ cos (5π/6)< 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
5. cos (2π/3) tg (π/4) = cos (2 180°/3) tg (180°/4) = cos 120° tg 45°. ჩვენ ვუყურებთ კოსინუსს: 120° ∈ არის II კოორდინატთა მეოთხედი, ამიტომ cos (2π/3)< 0. Смотрим на тангенс: 45° ∈ — это I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) >0. ისევ მივიღეთ პროდუქტი, რომელშიც სხვადასხვა ნიშნის ფაქტორებია. ვინაიდან „მინუს გამრავლებული პლუსი იძლევა მინუსს“, გვაქვს: cos (2π/3) tg (π/4)< 0;
6. sin (5π/6) cos (7π/4) = sin (5 180°/6) cos (7 180°/4) = sin 150° cos 315°. ჩვენ ვმუშაობთ სინუსზე: 150° ∈ დან ვსაუბრობთ II კოორდინატთა კვარტალზე, სადაც სინუსები დადებითია. ამიტომ, sin (5π/6) > 0. ანალოგიურად, 315° ∈ არის IV კოორდინატთა მეოთხედი, იქ კოსინუსები დადებითია. მაშასადამე, cos (7π/4) > 0. მივიღეთ ორის ნამრავლი დადებითი რიცხვებიეს გამოთქმა ყოველთვის დადებითია. ჩვენ ვასკვნით: sin (5π/6) cos (7π/4) > 0;
7. tg (3π/4) cos (5π/3) = tg (3 180°/4) cos (5 180°/3) = tg 135° cos 300°. მაგრამ კუთხე 135° ∈ არის მეორე მეოთხედი, ე.ი. რუჯი (3π/4)< 0. Аналогично, угол 300° ∈ — это IV четверть, т.е. cos (5π/3) >0. ვინაიდან „მინუს პლუსი იძლევა მინუს ნიშანს“, გვაქვს: tg (3π/4) cos (5π/3)< 0;
8. ctg (4π/3) tg (π/6) = ctg (4 180°/3) tg (180°/6) = ctg 240° tg 30°. ჩვენ ვუყურებთ კოტანგენტის არგუმენტს: 240° ∈ არის III კოორდინატთა მეოთხედი, შესაბამისად ctg (4π/3) > 0. ანალოგიურად, ტანგენსისთვის გვაქვს: 30° ∈ არის I კოორდინატთა მეოთხედი, ე.ი. უმარტივესი კუთხე. მაშასადამე, tg (π/6) > 0. ჩვენ კვლავ მივიღეთ ორი დადებითი გამოხატულება - მათი ნამრავლიც დადებითი იქნება. ამიტომ ctg (4π/3) tg (π/6) > 0.

და ბოლოს, მოდით შევხედოთ რამდენიმე უფრო რთულ პრობლემას. გარდა იმისა, რომ გაიგოთ ტრიგონომეტრიული ფუნქციის ნიშანი, აქ თქვენ უნდა გააკეთოთ პატარა გამოთვლა - ისევე, როგორც ეს კეთდება რეალურ ამოცანებში B11. პრინციპში, ეს არის თითქმის რეალური ამოცანები, რომლებიც ნამდვილად გვხვდება მათემატიკაში გამოცდაზე.

Დავალება. იპოვეთ sin α, თუ sin 2 α = 0,64 და α ∈ [π/2; π].

ვინაიდან sin 2 α = 0,64 გვაქვს: sin α = ±0,8. რჩება გადასაწყვეტი: პლუს თუ მინუსი? ვარაუდით, კუთხე α ∈ [π/2; π] არის II კოორდინატთა მეოთხედი, სადაც ყველა სინუსი დადებითია. მაშასადამე, sin α = 0.8 - ნიშნებით გაურკვევლობა აღმოფხვრილია.

Დავალება. იპოვეთ cos α, თუ cos 2 α = 0,04 და α ∈ [π; 3π/2].

ჩვენც ანალოგიურად ვიქცევით, ე.ი. ვიღებთ კვადრატულ ფესვს: cos 2 α = 0,04 ⇒ cos α = ±0,2. ვარაუდით, კუთხე α ∈ [π; 3π/2], ე.ი. საუბარია III კოორდინატულ კვარტალზე. იქ ყველა კოსინუსი უარყოფითია, ამიტომ cos α = -0,2.

Დავალება. იპოვეთ sin α, თუ sin 2 α = 0,25 და α ∈ .

გვაქვს: sin 2 α = 0,25 ⇒ sin α = ±0,5. ისევ ვუყურებთ კუთხეს: α ∈ არის IV კოორდინატთა მეოთხედი, რომელშიც, როგორც მოგეხსენებათ, სინუსი უარყოფითი იქნება. ამრიგად, დავასკვნათ: sin α = −0,5.

Დავალება. იპოვეთ tg α, თუ tg 2 α = 9 და α ∈.

ყველაფერი იგივეა, მხოლოდ ტანგენტისთვის. ვიღებთ კვადრატულ ფესვს: tg 2 α = 9 ⇒ tg α = ±3. მაგრამ პირობით, α ∈ კუთხე არის I კოორდინატის კვადრატი. ყველა ტრიგონომეტრიული ფუნქცია, მათ შორის. ტანგენსი, არის დადებითი, ამიტომ tg α = 3. ეს არის ის!