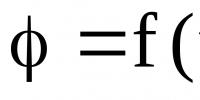Pamje e përgjithshme e matricave trekëndore:

Vini re se ndër elementet diagonale mund të ketë zero elementë. Matricë quhet trapez i sipërm nëse plotësohen tre kushtet e mëposhtme:

1. për i>j;

2. Ekziston një numër natyror r që plotëson pabarazitë , çfarë .

3. Nëse ndonjë element diagonal , atëherë të gjithë elementet i-të rreshti dhe të gjitha rreshtat pasardhës janë zero.

Pamje e përgjithshme e matricave trapezoidale të sipërme:

në .

në .

për r=n

në r=m=n.

Vini re se për r=m=n, matrica e sipërme trapezoidale është një matricë trekëndore me hyrje diagonale jo zero.

27) Veprimet me matrica

Shtimi i matricës

Mund të shtohen matrica me të njëjtën madhësi.

Shuma e dy matricave të tilla A dhe B është matrica C, elementet e së cilës janë të barabartë me shumën e elementeve përkatëse të matricave A dhe B. Në mënyrë simbolike do të shkruajmë si më poshtë: A+B=C.

Është e lehtë të shihet se mbledhja e matricës u bindet ligjeve komutative dhe shoqëruese:

(A+B)+C=A+(B+C).

Matrica zero gjatë mbledhjes së matricave kryen rolin e zeros së zakonshme gjatë mbledhjes së numrave: A+0=A.

Zbritja e matricës.

Dallimi i dy matricave A dhe B me të njëjtën madhësi është një matricë C e tillë që

Nga ky përkufizim del se elementet e matricës C janë të barabarta me diferencën e elementeve përkatëse të matricës A dhe B.

Dallimi i matricave A dhe B shënohet si më poshtë: C \u003d A - B.

3. Shumëzimi i matricës

Merrni parasysh rregullin për shumëzimin e dy matricave katrore të rendit të dytë.

Prodhimi i matricës A dhe matricës B është matrica C=AB.

Rregullat për shumëzimin e matricave drejtkëndore:

Shumëzimi i matricës A me matricën B ka kuptim nëse numri i kolonave në matricën A është i njëjtë me numrin e rreshtave në matricën B.

Si rezultat i shumëzimit të dy matricave drejtkëndëshe, fitohet një matricë që përmban po aq rreshta sa kishte rreshta në matricën e parë dhe aq kolona sa kishte kolona në matricën e dytë.

4. Shumëzimi i një matrice me një numër

Kur shumëzojmë matricën A me numrin , të gjithë numrat që përbëjnë matricën A shumëzohen me numrin . Për shembull, le të shumëzojmë matricën me numrin 2. Marrim, d.m.th. kur një matricë shumëzohet me një numër, faktori "futet" nën shenjën e matricës.

Transpozimi i matricës

Matrica e transpozuar është matrica AT e marrë nga matrica origjinale A duke zëvendësuar rreshtat me kolona.

Formalisht, matrica e transpozuar për një matricë m*n A është një matricë n*m AT, e përcaktuar si AT = A .

Për shembull,

Vetitë e matricave të transpozuara

2. (A + B)T = AT + BT

28) Koncepti i përcaktorit të rendit të n-të

Le të ketë një tabelë katrore të përbërë nga numra të renditur në n rreshta horizontale dhe n vertikale. Duke përdorur këta numra, sipas rregullave të caktuara, llogaritet një numër i caktuar, i cili quhet përcaktor i rendit të n-të dhe shënohet si më poshtë:

(1)

Rreshtat horizontale në përcaktorin (1) quhen rreshta, rreshtat vertikalë quhen kolona, ​​dhe numrat quhen elementë të përcaktorit (indeksi i parë nënkupton numrin e rreshtit, indeksi i dytë është numri i kolonës, në kryqëzimin e së cilës ndodhet një element; i = 1, 2, ..., n; j = 1, 2, ..., n). Rendi i një përcaktori është numri i rreshtave dhe kolonave të tij.

Një vijë e drejtë imagjinare që lidh elementet e përcaktorit për të cilin të dy indekset janë të njëjtë, d.m.th. elementet

quhet diagonalja kryesore, diagonalja tjetër quhet diagonale anësore.

Përcaktori i rendit të n-të është një numër që është shuma algjebrike e n-së! termat, secila prej të cilave është prodhimi i n prej elementeve të tij, i marrë vetëm një nga secili n rresht dhe nga secila n kolona e një tabele katrore me numra, me gjysmën e termave (të caktuara) të marra me shenjat e tyre, dhe pjesa tjetër me shenja të kundërta.

Le të tregojmë se si llogariten përcaktorët e tre renditjeve të para.

Përcaktori i rendit të parë është vetë elementi d.m.th.

Përcaktori i rendit të dytë është numri i marrë si më poshtë:

(2)

Formula (3) tregon se me shenjat e tyre merren terma që janë prodhim i elementeve të diagonales kryesore, si dhe elementë që ndodhen në kulmet e dy trekëndëshave, bazat e të cilëve janë paralele me të; me të kundërta - terma që janë produkte të elementeve të diagonales dytësore, si dhe elementë të vendosur në kulmet e dy trekëndëshave që janë paralel me të.

Shembulli 2. Llogaritni përcaktorin e rendit të tretë:

Zgjidhje. Duke përdorur rregullin e trekëndëshave, marrim

Llogaritja e përcaktorëve të rendit të katërt dhe të mëpasshëm mund të reduktohet në llogaritjen e përcaktorëve të rendit të dytë dhe të tretë. Kjo mund të bëhet duke përdorur vetitë e përcaktorëve. Tani i drejtohemi shqyrtimit të tyre.

Vetitë e përcaktorit të rendit të n-të

Vetia 1. Me rastin e zëvendësimit të rreshtave me kolona (transpozimi), vlera e përcaktorit nuk do të ndryshojë, d.m.th.

Vetia 2. Nëse të paktën një rresht (rresht ose kolonë) përbëhet nga zero, atëherë përcaktorja është e barabartë me zero. Prova është e qartë.

Në të vërtetë, atëherë në çdo term të përcaktorit një nga faktorët do të jetë zero.

Vetia 3. Nëse dy rreshta paralelë ngjitur (rreshta ose kolona) ndërrohen në përcaktor, atëherë përcaktorja do të ndryshojë shenjën në të kundërtën, d.m.th.

Vetia 4. Nëse ka dy rreshta paralelë identikë në përcaktor, atëherë përcaktorja është e barabartë me zero:

Vetia 5. Nëse dy rreshta paralelë në përcaktor janë proporcionale, atëherë përcaktorja është e barabartë me zero:

Vetia 6. Nëse të gjithë elementët e përcaktorit në të njëjtën rresht shumëzohen me të njëjtin numër, atëherë vlera e përcaktorit do të ndryshojë këtë numër herë:

Pasoja. Faktori i përbashkët i përfshirë në të gjithë elementët e së njëjtës rresht mund të hiqet nga shenja përcaktuese, për shembull:

Vetia 7. Nëse në përcaktor të gjithë elementët e një rreshti paraqiten si shumë e dy termave, atëherë ai është e barabartë me shumën dy përcaktues:

Vetia 8. Nëse i shtojmë produktin e elementeve përkatës të një serie paralele me një faktor konstant elementeve të çdo serie, atëherë vlera e përcaktorit nuk do të ndryshojë:

Vetia 9. Nëse elementeve të rreshtit të i-të i shtohet një kombinim linear i elementeve përkatëse të disa rreshtave paralelë, atëherë vlera e përcaktorit nuk do të ndryshojë:

Kurbat e rendit të dytë në një rrafsh quhen vija të përcaktuara me ekuacione në të cilat variabla koordinon x dhe y të përfshira në shkallën e dytë. Këto përfshijnë elipsin, hiperbolën dhe parabolën.

Forma e përgjithshme e ekuacionit të kurbës së rendit të dytë është si më poshtë:

ku A, B, C, D, E, F- numrat dhe të paktën një nga koeficientët A, B, C nuk është e barabartë me zero.

Kur zgjidhen problema me kthesa të rendit të dytë, më së shpeshti merren parasysh ekuacionet kanonike të një elipse, hiperbole dhe parabole. Është e lehtë t'u kalosh atyre nga ekuacionet e përgjithshme, shembulli 1 i problemeve me elipsat do t'i kushtohet kësaj.

Elipsa e dhënë nga ekuacioni kanonik

Përkufizimi i një elipsi. Një elipsë është bashkësia e të gjitha pikave në rrafsh, ato për të cilat shuma e distancave me pikat, të quajtura vatra, është një konstante dhe më e madhe se distanca ndërmjet vatrave.

Fokuset janë shënuar si në figurën më poshtë.

Ekuacioni kanonik i një elipsi është:

ku a dhe b (a > b) - gjatësitë e gjysmëboshteve, d.m.th., gjysma e gjatësisë së segmenteve të prera nga elipsi në boshtet koordinative.

Vija e drejtë që kalon nëpër vatrat e elipsës është boshti i saj i simetrisë. Një bosht tjetër i simetrisë së elipsës është një vijë e drejtë që kalon nga mesi i segmentit pingul me këtë segment. Pika O kryqëzimi i këtyre vijave shërben si qendra e simetrisë së elipsës, ose thjesht qendra e elipsës.

Boshti i abshisës i elipsës kryqëzohet në pika ( a, O) dhe (- a, O), dhe boshti y është në pika ( b, O) dhe (- b, O). Këto katër pika quhen kulme të elipsës. Segmenti midis kulmeve të elipsës në boshtin e abshisës quhet boshti i tij kryesor, dhe në boshtin e ordinatave - boshti i vogël. Segmentet e tyre nga maja në qendër të elipsës quhen gjysmëboshte.

Nese nje a = b, atëherë ekuacioni i elipsës merr formën . Ky është ekuacioni për një rreth me rreze a, dhe një rreth është një rast i veçantë i një elipsi. Një elipsë mund të merret nga një rreth me rreze a, nëse e ngjesh në a/b herë përgjatë boshtit Oy .

Shembulli 1 Kontrolloni nëse vija e dhënë nga ekuacioni i përgjithshëm , një elips.

Zgjidhje. Ne bëjmë transformime ekuacioni i përgjithshëm. Zbatojmë transferimin e termit të lirë në anën e djathtë, ndarjen term pas termi të ekuacionit me të njëjtin numër dhe reduktimin e thyesave:

Përgjigju. Ekuacioni që rezulton është ekuacioni kanonik i elipsës. Prandaj, kjo linjë është një elips.

Shembulli 2 Shkruani ekuacionin kanonik të një elipse nëse gjysmëboshtet e saj janë përkatësisht 5 dhe 4.

Zgjidhje. Ne shikojmë formulën për ekuacionin kanonik të elipsës dhe zëvendësojmë: boshti gjysmë i madh është a= 5, gjysmëboshti i vogël është b= 4. Marrim ekuacionin kanonik të elipsës:

Pikat dhe shënohen me të gjelbër në aksin kryesor, ku

thirrur truket.

thirrur ekscentricitet elips.

Qëndrimi b/a karakterizon "shtresën" e elipsës. Sa më i vogël ky raport, aq më shumë zgjatet elipsa përgjatë boshtit kryesor. Sidoqoftë, shkalla e zgjatjes së elipsës shprehet më shpesh në terma të ekscentricitetit, formula e së cilës është dhënë më sipër. Për elipsa të ndryshme, ekscentriciteti varion nga 0 në 1, duke mbetur gjithmonë më pak se një.

Shembulli 3 Shkruani ekuacionin kanonik të një elipsi nëse distanca midis vatërve është 8 dhe boshtit kryesor është 10.

Zgjidhje. Ne nxjerrim përfundime të thjeshta:

Nëse boshti kryesor është 10, atëherë gjysma e tij, d.m.th., gjysmëboshti a = 5 ,

Nëse distanca midis vatrave është 8, atëherë numri c e koordinatave të fokusit është 4.

Zëvendësoni dhe llogaritni:

Rezultati është ekuacioni kanonik i elipsës:

Shembulli 4 Shkruani ekuacionin kanonik të një elipse nëse boshti i saj kryesor është 26 dhe ekscentriciteti është .

Zgjidhje. Siç del si nga madhësia e boshtit të madh ashtu edhe nga ekuacioni i ekscentricitetit, gjysmëboshti kryesor i elipsës a= 13. Nga ekuacioni i ekscentricitetit, ne shprehim numrin c, e nevojshme për të llogaritur gjatësinë e gjysmëboshtit të vogël:

.

Ne llogarisim katrorin e gjatësisë së gjysmëboshtit të vogël:

Ne hartojmë ekuacionin kanonik të elipsës:

Shembulli 5 Përcaktoni vatrat e elipsës të dhëna nga ekuacioni kanonik.

Zgjidhje. Duhet gjetur një numër c, i cili përcakton koordinatat e para të vatrave të elipsës:

.

Ne marrim fokuset e elipsit:

Shembulli 6 Fokuset e elipsës janë të vendosura në bosht kau simetrike për origjinën. Shkruani ekuacionin kanonik të një elipsi nëse:

1) distanca midis vatrave është 30, dhe boshti kryesor është 34

2) boshti i vogël është 24, dhe një nga fokuset është në pikën (-5; 0)

3) ekscentriciteti, dhe një nga fokuset është në pikën (6; 0)

Ne vazhdojmë të zgjidhim problemet në elips së bashku

Nëse - një pikë arbitrare e elipsës (e shënuar me të gjelbër në vizatim në pjesën e sipërme të djathtë të elipsë) dhe - distancat në këtë pikë nga vatrat, atëherë formulat për distancat janë si më poshtë:

Për çdo pikë që i përket elipsit, shuma e distancave nga vatrat është një vlerë konstante e barabartë me 2 a.

Vijat e drejta të përcaktuara me ekuacione

thirrur drejtorët elips (në vizatim - vija të kuqe përgjatë skajeve).

Nga dy barazimet e mësipërme rezulton se për çdo pikë të elipsës

,

ku dhe janë distancat e kësaj pike me drejtimet dhe .

Shembulli 7 Jepet një elips. Shkruani një ekuacion për direktrikat e tij.

Zgjidhje. Ne shikojmë në ekuacionin e drejtpërdrejtë dhe zbulojmë se kërkohet të gjejmë ekscentricitetin e elipsës, d.m.th. Të gjitha të dhënat për këtë janë. Ne llogarisim:

.

Marrim ekuacionin e drejtimit të elipsës:

Shembulli 8 Shkruani ekuacionin kanonik të një elipsi nëse vatrat e saj janë pika dhe drejtimet janë drejtëza.

Linjat e rendit të dytë.
Elipsa dhe ekuacioni i saj kanonik. Rretho

Pas një studimi të plotë vija të drejta në aeroplan ne vazhdojmë të studiojmë gjeometrinë e botës dydimensionale. Aksionet janë dyfishuar dhe ju ftoj të vizitoni galerinë piktoreske të elipsave, hiperbolave, parabolave, të cilat janë përfaqësuese tipike të linjat e rendit të dytë. Turneu tashmë ka filluar, dhe së pari, një informacion i shkurtër për të gjithë ekspozitën në kate të ndryshme të muzeut:

Koncepti i një linje algjebrike dhe renditja e saj

Një vijë në një aeroplan quhet algjebrike, nëse në sistemi i koordinatave afinale ekuacioni i tij ka formën , ku është një polinom i përbërë nga termat e formës (është një numër real, janë numra të plotë jo negativë).

Siç mund ta shihni, ekuacioni i një linje algjebrike nuk përmban sinus, kosinus, logaritme dhe beau monde të tjera funksionale. Vetëm "x" dhe "y" në numër i plotë jo negativ gradë.

Rendi i linjësështë e barabartë me vlerën maksimale të termave të përfshirë në të.

Sipas teoremës përkatëse, koncepti i një linje algjebrike, si dhe rendi i saj, nuk varen nga zgjedhja sistemi i koordinatave afinale, prandaj, për lehtësinë e qenies, konsiderojmë se të gjitha llogaritjet e mëvonshme bëhen në Koordinatat karteziane.

Ekuacioni i Përgjithshëm rreshti i rendit të dytë ka formën , ku - arbitrare numra realë (është zakon të shkruhet me një shumëzues - "dy"), dhe koeficientët nuk janë njëkohësisht të barabartë me zero.

Nëse , atëherë ekuacioni thjeshtohet në , dhe nëse koeficientët nuk janë njëkohësisht të barabartë me zero, atëherë kjo është saktësisht ekuacioni i përgjithshëm i një vije të drejtë "të sheshtë"., që përfaqëson linjë e rendit të parë.

Shumë e kuptuan kuptimin e termave të rinj, por, megjithatë, për të asimiluar 100% materialin, ne i fusim gishtat në prizë. Për të përcaktuar rendin e rreshtit, përsëritni përsëri të gjitha kushtet ekuacionet e tij dhe për secilën prej tyre gjeni shuma e fuqive variablat hyrëse.

Për shembull:

termi përmban "x" deri në shkallën e parë;
termi përmban "Y" deri në shkallën 1;
nuk ka variabla në term, kështu që shuma e fuqive të tyre është zero.

Tani le të kuptojmë pse ekuacioni vendos vijën e dyta porosit:

termi përmban "x" në shkallën e dytë;
termi ka shumën e shkallëve të variablave: 1 + 1 = 2;
termi përmban "y" në shkallën e dytë;
të gjitha kushtet e tjera - më i vogël shkallë.

Vlera maksimale: 2

Nëse shtojmë shtesë në ekuacionin tonë, të themi, atëherë ai tashmë do të përcaktojë linjë e rendit të tretë. Është e qartë se forma e përgjithshme e ekuacionit të linjës së rendit të tretë përmban një "bashkësi të plotë" termash, shuma e shkallëve të variablave në të cilat është e barabartë me tre:
, ku koeficientët nuk janë njëkohësisht të barabartë me zero.

Në rast se shtohen një ose më shumë terma të përshtatshëm që përmbajnë , atëherë do të flasim Linjat e rendit të 4-të, etj.

Ne do të duhet të merremi me linjat algjebrike të rendit të tretë, të katërt dhe më të lartë më shumë se një herë, veçanërisht kur të njihemi me sistemi i koordinatave polar.

Megjithatë, le të kthehemi te ekuacioni i përgjithshëm dhe të kujtojmë variacionet e tij më të thjeshta shkollore. Shembuj janë parabola, ekuacioni i së cilës mund të reduktohet lehtësisht në një formë të përgjithshme, dhe hiperbola me një ekuacion ekuivalent. Sidoqoftë, jo gjithçka është aq e qetë….

Një pengesë e rëndësishme e ekuacionit të përgjithshëm është se pothuajse gjithmonë nuk është e qartë se cilën linjë përcakton. Edhe në rastin më të thjeshtë, nuk do ta kuptoni menjëherë se kjo është hiperbolë. Paraqitjet e tilla janë të mira vetëm në një maskaradë, prandaj, në rrjedhën e gjeometrisë analitike, konsiderohet një problem tipik reduktimi i ekuacionit të linjës së rendit të dytë në formën kanonike.

Cila është forma kanonike e një ekuacioni?

Kjo është forma standarde e pranuar përgjithësisht e ekuacionit, kur brenda pak sekondash bëhet e qartë se çfarë objekti gjeometrik përcakton. Për më tepër, forma kanonike është shumë e përshtatshme për zgjidhjen e shumë problemeve praktike. Kështu, për shembull, sipas ekuacionit kanonik "i sheshtë" drejt, së pari, është menjëherë e qartë se kjo është një vijë e drejtë, dhe së dyti, pika që i përket dhe vektori i drejtimit janë thjesht të dukshme.

Natyrisht, çdo Linja e rendit të parë përfaqëson një vijë të drejtë. Në katin e dytë, nuk na pret më një portier, por një shoqëri shumë më e larmishme prej nëntë statujash:

Klasifikimi i linjave të rendit të dytë

Me ndihmën e një grupi të veçantë veprimesh, çdo ekuacion i linjës së rendit të dytë reduktohet në një nga llojet e mëposhtme:

(dhe janë numra realë pozitivë)

1) është ekuacioni kanonik i elipsës;

2) është ekuacioni kanonik i hiperbolës;

3) është ekuacioni kanonik i parabolës;

4) – imagjinare elips;

5) - një palë vijash kryqëzuese;

6) - çift imagjinare vija kryqëzuese (me pikën e vetme reale të kryqëzimit në origjinë);

7) - një palë linja paralele;

8) - çift imagjinare vija paralele;

9) është një çift vijash që përputhen.

Disa lexues mund të kenë përshtypjen se lista është e paplotë. Për shembull, në paragrafin numër 7, ekuacioni vendos çiftin e drejtpërdrejtë, paralel me boshtin, dhe lind pyetja: ku ndodhet ekuacioni që përcakton drejtëzat paralele me boshtin y? Përgjigje: ajo nuk konsiderohet kanun. Vijat e drejta përfaqësojnë të njëjtin rast standard të rrotulluar me 90 gradë, dhe një hyrje shtesë në klasifikim është e tepërt, pasi nuk ka asgjë thelbësisht të re.

Kështu, ekzistojnë nëntë dhe vetëm nëntë lloje të ndryshme të linjave të rendit të dytë, por në praktikë janë më të zakonshmet elipsa, hiperbola dhe parabola.

Le të shohim së pari elipsin. Si zakonisht, unë përqendrohem në ato pika që kanë një rëndësi të madhe për zgjidhjen e problemeve, dhe nëse keni nevojë për një derivim të detajuar të formulave, vërtetimeve të teoremave, ju lutemi referojuni, për shembull, tekstit shkollor nga Bazylev / Atanasyan ose Aleksandrov.

Elipsa dhe ekuacioni i saj kanonik

Drejtshkrimi ... ju lutemi mos përsëritni gabimet e disa përdoruesve të Yandex të cilët janë të interesuar "si të ndërtoni një elips", "dallimi midis një elipsi dhe një ovale" dhe "ekscentriciteti i Elebs".

Ekuacioni kanonik i një elipsi ka formën , ku janë numra realë pozitivë dhe . Unë do të formuloj përkufizimin e një elipsi më vonë, por tani për tani është koha për të marrë një pushim nga të folurit dhe për të zgjidhur një problem të zakonshëm:

Si të ndërtoni një elips?

Po, merre dhe thjesht vizato. Detyra është e zakonshme dhe një pjesë e konsiderueshme e studentëve nuk e përballojnë me kompetencë vizatimin:

Shembulli 1

Ndërtoni një elipsë të dhënë nga ekuacioni

Zgjidhje: fillimisht e sjellim ekuacionin në formën kanonike:

Pse të sjellë? Një nga avantazhet e ekuacionit kanonik është se ju lejon të përcaktoni menjëherë kulmet elipsore, të cilat janë në pikat . Është e lehtë të shihet se koordinatat e secilës prej këtyre pikave plotësojnë ekuacionin.

Në këtë rast :


Segmenti i linjës thirrur boshti kryesor elips;
segmenti i linjës – aks i vogël;
numri thirrur aks gjysmë i madh elips;
numri – aks gjysmë i vogël.
në shembullin tonë: .

Për të imagjinuar shpejt se si duket kjo apo ajo elips, thjesht shikoni vlerat e "a" dhe "be" të ekuacionit të saj kanonik.

Gjithçka është në rregull, e rregullt dhe e bukur, por ka një paralajmërim: Unë e përfundova vizatimin duke përdorur programin. Dhe mund të vizatoni me çdo aplikacion. Sidoqoftë, në realitetin e ashpër, një copë letre me kuadrate shtrihet në tryezë dhe minjtë kërcejnë rreth duarve tona. Njerëzit me talent artistik, natyrisht, mund të debatojnë, por ju keni edhe minj (ndonëse më të vegjël). Jo më kot njerëzimi shpiku një sundimtar, një busull, një raportues dhe pajisje të tjera të thjeshta për vizatim.

Për këtë arsye, nuk ka gjasa të jemi në gjendje të vizatojmë me saktësi një elips, duke ditur vetëm kulmet. Ende në rregull, nëse elipsi është i vogël, për shembull, me gjysmëboshte. Përndryshe, ju mund të zvogëloni shkallën dhe, në përputhje me rrethanat, dimensionet e vizatimit. Por në rastin e përgjithshëm është shumë e dëshirueshme të gjenden pika shtesë.

Ekzistojnë dy qasje për ndërtimin e një elipsi - gjeometrike dhe algjebrike. Nuk më pëlqen ndërtimi me busull dhe vizore për shkak të algoritmit të shkurtër dhe rrëmujës së konsiderueshme të vizatimit. Në rast urgjence, ju lutemi referojuni tekstit shkollor, por në realitet është shumë më racionale të përdoren mjetet e algjebrës. Nga ekuacioni i elipsit në draft, ne shprehim shpejt:

Ekuacioni më pas ndahet në dy funksione:
– përcakton harkun e sipërm të elipsës;
– përcakton harkun e poshtëm të elipsës.

Elipsa e dhënë nga ekuacioni kanonik është simetrik në lidhje me boshtet koordinative, si dhe në lidhje me origjinën. Dhe kjo është e shkëlqyeshme - simetria është pothuajse gjithmonë një pararojë e një të lirë. Natyrisht, mjafton të merremi me tremujorin e 1-rë të koordinatave, ndaj na duhet një funksion . Ai sugjeron gjetjen e pikave shtesë me abscissas . Ne goditëm tre SMS në kalkulator:

Sigurisht, është gjithashtu e këndshme që nëse bëhet një gabim serioz në llogaritjet, atëherë kjo menjëherë do të bëhet e qartë gjatë ndërtimit.

Shënoni pikat në vizatim (ngjyra e kuqe), pikat simetrike në harqet e tjera (ngjyra blu) dhe lidhni me kujdes të gjithë kompaninë me një vijë:


Është më mirë të vizatoni skicën fillestare hollë dhe hollë, dhe vetëm atëherë të bëni presion në laps. Rezultati duhet të jetë një elips mjaft i mirë. Nga rruga, do të dëshironit të dini se çfarë është kjo kurbë?

Përkufizimi i një elipsi. Vatra elipsore dhe ekscentriciteti i elipseve

Një elipsë është një rast i veçantë i një ovali. Fjala "ovale" nuk duhet kuptuar në kuptimin filistin ("fëmija vizatoi një ovale" etj.). Ky është një term matematikor me një formulim të detajuar. Qëllimi i këtij mësimi nuk është të merret në konsideratë teoria e ovaleve dhe llojet e tyre të ndryshme, të cilave praktikisht nuk u kushtohet vëmendje në kursin standard të gjeometrisë analitike. Dhe, në përputhje me nevojat më aktuale, ne shkojmë menjëherë në përkufizimin e rreptë të një elipsi:

Elipsa- kjo është bashkësia e të gjitha pikave të rrafshit, shuma e largësive në secilën prej të cilave nga dy pika të dhëna, të quajtura truket elipsa, është një vlerë konstante, numerikisht e barabartë me gjatësinë e boshtit kryesor të kësaj elipse: .
Në këtë rast, distanca midis vatrave është më e vogël se kjo vlerë: .

Tani do të bëhet më e qartë:

Imagjinoni që pika blu "kalëron" në një elips. Pra, pavarësisht nga pika e elipsës që marrim, shuma e gjatësive të segmenteve do të jetë gjithmonë e njëjtë:

Le të sigurohemi që në shembullin tonë vlera e shumës të jetë vërtet e barabartë me tetë. Vendosni mendërisht pikën "em" në kulmin e djathtë të elipsës, pastaj: , e cila kërkohej të kontrollohej.

Një mënyrë tjetër për të vizatuar një elipsë bazohet në përkufizimin e një elipsi. Matematika e lartë, nganjëherë, është shkaku i tensionit dhe stresit, kështu që është koha për të bërë një seancë tjetër shkarkimi. Ju lutemi merrni një copë letre ose një fletë të madhe kartoni dhe ngjiteni në tryezë me dy gozhdë. Këto do të jenë truket. Lidhni një fije jeshile në kokat e thonjve të dalë dhe tërhiqeni deri në fund me një laps. Qafa e lapsit do të jetë në një pikë, e cila i përket elipsit. Tani filloni ta drejtoni lapsin nëpër fletën e letrës, duke e mbajtur fillin e gjelbër shumë të tendosur. Vazhdoni procesin derisa të ktheheni në pikën e fillimit ... shkëlqyeshëm ... vizatimi mund të dorëzohet për verifikim nga mjeku te mësuesi =)

Si të gjeni fokusin e një elipsi?

Në shembullin e mësipërm, unë përshkrova pikat e fokusit "të gatshme", dhe tani do të mësojmë se si t'i nxjerrim ato nga thellësitë e gjeometrisë.

Nëse elipsa jepet nga ekuacioni kanonik, atëherë vatrat e saj kanë koordinata , ku eshte distanca nga secila prej vatrave deri te qendra e simetrisë së elipsës.

Llogaritjet janë më të lehta se rrepat e zier me avull:

! Me kuptimin "ce" është e pamundur të identifikohen koordinatat specifike të mashtrimeve! E përsëris, kjo është DISTANCA nga çdo fokus në qendër(që në rastin e përgjithshëm nuk ka pse të gjendet pikërisht në origjinë).
Dhe, për rrjedhojë, distanca midis vatrave nuk mund të lidhet as me pozicionin kanonik të elipsit. Me fjalë të tjera, elipsa mund të zhvendoset në një vend tjetër dhe vlera do të mbetet e pandryshuar, ndërsa truket, natyrisht, do të ndryshojnë koordinatat e tyre. Ju lutemi, mbani në mend këtë kur e eksploroni më tej temën.

Ekscentriciteti i një elipsi dhe kuptimi i tij gjeometrik

Ekscentriciteti i një elipsi është një raport që mund të marrë vlera brenda.

Në rastin tonë:

Le të zbulojmë se si forma e një elipsi varet nga ekscentriciteti i saj. Për këtë rregulloni kulmet majtas dhe djathtas e elipsës në shqyrtim, pra vlera e boshtit gjysmë të madh do të mbetet konstante. Atëherë formula e ekscentricitetit do të marrë formën: .

Le të fillojmë të përafrojmë vlerën e ekscentricitetit me unitetin. Kjo është e mundur vetëm nëse. Çfarë do të thotë? ...duke kujtuar truket . Kjo do të thotë që vatrat e elipsës do të "shpërndahen" përgjatë boshtit të abshisës në kulmet anësore. Dhe, meqenëse "segmentet e gjelbra nuk janë gome", elipsa në mënyrë të pashmangshme do të fillojë të rrafshohet, duke u shndërruar në një sallam më të hollë dhe më të hollë të varur në bosht.

Në këtë mënyrë, sa më afër njëshit të jetë ekscentriciteti i elipsës, aq më e zgjatur është elipsa.

Tani le të simulojmë procesin e kundërt: vatrat e elipsës shkuan drejt njëri-tjetrit, duke iu afruar qendrës. Kjo do të thotë se vlera e "ce" po bëhet më e vogël dhe, në përputhje me rrethanat, ekscentriciteti tenton në zero: .
Në këtë rast, "segmentet e gjelbra", përkundrazi, do të "bëhen të mbushura me njerëz" dhe ata do të fillojnë të "shtyjnë" vijën e elipsit lart e poshtë.

Në këtë mënyrë, sa më afër zeros të jetë vlera e ekscentricitetit, aq më shumë duket elipsa... shikoni rastin kufizues, kur vatrat ribashkohen me sukses në origjinë:

Një rreth është një rast i veçantë i një elipsi

Në të vërtetë, në rastin e barazisë së gjysmëboshteve, ekuacioni kanonik i elipsës merr formën, i cili në mënyrë refleksive shndërrohet në ekuacionin e njohur rrethor nga shkolla me qendër në origjinën e rrezes "a".

Në praktikë, shënimi me shkronjën "e folur" "er" përdoret më shpesh:. Rrezja quhet gjatësia e segmentit, ndërsa secila pikë e rrethit largohet nga qendra me distancën e rrezes.

Vini re se përkufizimi i një elipsi mbetet plotësisht i saktë: vatrat përputhen, dhe shuma e gjatësive të segmenteve të përputhura për secilën pikë në rreth është një vlerë konstante. Meqenëse distanca ndërmjet vatrave është ekscentriciteti i çdo rrethi është zero.

Një rreth ndërtohet lehtë dhe shpejt, mjafton të armatoseni me një busull. Sidoqoftë, ndonjëherë është e nevojshme të zbulohen koordinatat e disa pikave të tij, në këtë rast ne shkojmë në mënyrën e njohur - e sjellim ekuacionin në një formë të gëzuar të Matanit:

është funksioni i gjysmërrethit të sipërm;
është funksioni i gjysmërrethit të poshtëm.

Pastaj gjejmë vlerat e dëshiruara, të diferencueshme, integrohen dhe bëni gjëra të tjera të mira.

Artikulli, natyrisht, është vetëm për referencë, por si mund të jetohet pa dashuri në botë? Detyrë krijuese për vendim i pavarur

Shembulli 2

Hartoni ekuacionin kanonik të një elipsi nëse njihen një nga vatrat e saj dhe boshti gjysmë i vogël (qendra është në origjinë). Gjeni kulme, pika shtesë dhe vizatoni një vijë në vizatim. Llogaritni ekscentricitetin.

Zgjidhje dhe vizatim në fund të orës së mësimit

Le të shtojmë një veprim:

Rrotulloni dhe përktheni një elips

Le të kthehemi te ekuacioni kanonik i elipsës, përkatësisht te kushti, gjëegjëza e së cilës i mundon mendjet kureshtare që nga përmendja e parë e kësaj kurbë. Këtu kemi konsideruar një elips , por në praktikë nuk mundet ekuacioni ? Në fund të fundit, megjithatë, këtu duket se është si një elips!

Një ekuacion i tillë është i rrallë, por haset. Dhe përcakton një elips. Le të shpërndajmë mistikun:

Si rezultat i ndërtimit, fitohet elipsa jonë amtare, e rrotulluar me 90 gradë. Kjo eshte, - kjo është hyrje jokanonike elips . Regjistro!- ekuacioni nuk specifikon asnjë elipsë tjetër, pasi nuk ka pika (foci) në bosht që do të kënaqnin përkufizimin e një elipsi.

Ekuacioni kanonik i një elipsi ka formën

ku a është boshti gjysmë i madh; b - gjysmë boshti i vogël. Quhen pikat F1(c,0) dhe F2(-c,0) − c

a, b - gjysmëboshtet e elipsës.

Gjetja e vatrave, ekscentricitetit, drejtimit të një elipse nëse dihet ekuacioni kanonik i saj.

Përkufizimi i një hiperbole. Vatra hiperbole.

Përkufizimi. Një hiperbolë është një grup pikash në një rrafsh për të cilin moduli i diferencës në distancë nga dy pika të dhëna, të quajtura vatra, është një vlerë konstante, më e vogël se distanca midis vatrave.

Sipas përkufizimit, |r1 – r2|= 2a. F1, F2 janë vatra të hiperbolës. F1F2 = 2c.

Ekuacioni kanonik i një hiperbole. Gjysmë boshtet e një hiperbole. Ndërtimi i hiperbolës nëse dihet ekuacioni kanonik i saj.

Ekuacioni kanonik:

Boshti gjysmë i madh i hiperbolës është gjysma e distancës minimale midis dy degëve të hiperbolës, në anët pozitive dhe negative të boshtit (majtas dhe djathtas në raport me origjinën). Për një degë të vendosur në anën pozitive, gjysmë-boshti do të jetë i barabartë me:

Nëse e shprehim në terma të seksionit konik dhe të ekscentricitetit, atëherë shprehja do të marrë formën:

Gjetja e vatrave, ekscentricitetit, drejtimit të një hiperbole nëse dihet ekuacioni kanonik i saj.

Ekscentriciteti i një hiperbole

Përkufizimi. Raporti quhet ekscentricitet i hiperbolës, ku c -

gjysma e distancës ndërmjet vatrave, dhe është gjysmëboshti i vërtetë.

Duke marrë parasysh faktin se c2 - a2 = b2:

Nëse a \u003d b, e \u003d, atëherë hiperbola quhet barabrinjës (barabrinjës).

Drejtorët e hiperbolës

Përkufizimi. Dy drejtëza pingul me boshtin real të hiperbolës dhe të vendosura në mënyrë simetrike rreth qendrës në një distancë a/e prej saj quhen direktrika të hiperbolës. Ekuacionet e tyre janë:

Teorema. Nëse r është distanca nga një pikë arbitrare M e hiperbolës në një fokus, d është distanca nga e njëjta pikë në drejtimin që korrespondon me këtë fokus, atëherë raporti r/d është një vlerë konstante e barabartë me ekscentricitetin.

Përkufizimi i një parabole. Fokusi dhe drejtimi i një parabole.

Parabola. Një parabolë është vendndodhja e pikave, secila prej të cilave është njësoj e largët nga një pikë e caktuar fikse dhe nga një vijë e caktuar fikse. Pika e përmendur në përkufizim quhet fokusi i parabolës, dhe vija e drejtë quhet drejtimi i saj.

Ekuacioni kanonik i një parabole. parametri i parabolës. Ndërtimi i një parabole.

Ekuacioni kanonik i një parabole në një sistem koordinativ drejtkëndor është: (ose nëse boshtet janë të kundërta).

Ndërtimi i një parabole për një vlerë të caktuar të parametrit p kryhet në sekuencën vijuese:

Vizato boshtin e simetrisë së parabolës dhe vendos mbi të segmentin KF=p;

Drejtorksi DD1 vizatohet përmes pikës K pingul me boshtin e simetrisë;

Segmenti KF ndahet në gjysmë për të marrë kulmin 0 të parabolës;

Një numër pikash arbitrare 1, 2, 3, 5, 6 maten nga lart me një distancë gradualisht në rritje midis tyre;

Nëpër këto pika vizatohen drejtëza ndihmëse pingul me boshtin e parabolës;

Në vijat e drejta ndihmëse, serifet bëhen me një rreze të barabartë me distancën nga vija e drejtë në drejtim;

Pikat që rezultojnë janë të lidhura me një kurbë të lëmuar.