Termin (modul) u doslovnom prijevodu sa latinskog znači "mjera". Ovaj koncept je u matematiku uveo engleski naučnik R. Cotes. A njemački matematičar K. Weierstrass uveo je znak modula - simbol kojim se ovaj koncept označava prilikom pisanja.

U kontaktu sa

Po prvi put se ovaj koncept izučava u matematici u okviru programa 6. razreda srednje škole. Prema jednoj definiciji, modul je apsolutna vrijednost realnog broja. Drugim riječima, da biste saznali modul realnog broja, morate odbaciti njegov predznak.

Grafički apsolutna vrijednost a označeno kao |a|.

Glavna karakteristika ovog koncepta je da je on uvijek nenegativna vrijednost.

Brojevi koji se međusobno razlikuju samo predznakom nazivaju se suprotni brojevi. Ako je vrijednost pozitivna, onda je njena suprotnost negativna, a nula je njena vlastita suprotnost.

geometrijska vrijednost

Ako koncept modula razmatramo sa stanovišta geometrije, tada će on označavati udaljenost, koja se mjeri u jediničnim segmentima od početka do dati poen. Ova definicija u potpunosti otkriva geometrijsko značenje pojma koji se proučava.

Grafički, to se može izraziti na sljedeći način: |a| = O.A.

Svojstva apsolutne vrijednosti

U nastavku ćemo razmotriti sva matematička svojstva ovog koncepta i načine pisanja u obliku doslovnih izraza:

Osobine rješavanja jednačina s modulom

Ako govorimo o rješavanju matematičkih jednadžbi i nejednačina koje sadrže modul, onda morate zapamtiti da ćete morati otvoriti ovaj znak da biste ih riješili.

Na primjer, ako znak apsolutne vrijednosti sadrži neki matematički izraz, tada je prije otvaranja modula potrebno uzeti u obzir trenutne matematičke definicije.

|A + 5| = A + 5 ako je A veće ili jednako nuli.

5-A ako je A manje od nule.

U nekim slučajevima, znak se može nedvosmisleno proširiti za bilo koju vrijednost varijable.

Razmotrimo još jedan primjer. Konstruirajmo koordinatnu liniju, na kojoj označavamo sve numeričke vrijednosti, čija će apsolutna vrijednost biti 5.

Prvo morate nacrtati koordinatnu liniju, označiti ishodište koordinata na njoj i postaviti veličinu jednog segmenta. Osim toga, linija mora imati smjer. Sada je na ovoj pravoj liniji potrebno primijeniti oznake koje će biti jednake vrijednosti jednog segmenta.

Dakle, možemo vidjeti da će na ovoj koordinatnoj liniji biti dvije točke koje nas zanimaju sa vrijednostima 5 i -5.

MBOU srednja škola №17 Ivanov

« Modulo jednadžbe»
Metodički razvoj

Kompajlirano

nastavnik matematike

Lebedeva N.V.

20010

Objašnjenje

Poglavlje 1 Uvod

Odjeljak 2. Glavne karakteristike Odjeljak 3. Geometrijska interpretacija pojma modula broja Odjeljak 4. Grafikon funkcije y = |x| Odjeljak 5 Konvencije

Poglavlje 2

Odjeljak 1. Jednačine oblika |F(h)| = m (protozoa) Odjeljak 2. Jednačine oblika F(|h|) = m Odjeljak 3. Jednačine oblika |F(h)| = G(x) Odjeljak 4. Jednačine oblika |F(h)| = ± F(x) (prelijepo) Odjeljak 5. Jednačine oblika |F(h)| = |G(x)| Odjeljak 6. Primjeri rješavanja nestandardnih jednačina Odjeljak 7. Jednačine oblika |F(h)| + |G(x)| = 0 Odjeljak 8. Jednačine oblika |a 1 x ± v 1 | ± |a 2 x ± u 2 | ± …|a n x ± u n | = m Odjeljak 9. Jednačine koje sadrže više modula

Poglavlje 3. Primjeri rješavanja različitih jednačina sa modulom.

Odjeljak 1. Trigonometrijske jednadžbe Odjeljak 2 eksponencijalne jednačine Odjeljak 3. Logaritamske jednačine Odjeljak 4. Iracionalne jednačine Odjeljak 5. Zadaci napredne složenosti Odgovori na vježbe Bibliografija

Objašnjenje.

Koncept apsolutne vrijednosti (modula) realnog broja jedna je od njegovih bitnih karakteristika. Ovaj koncept se široko koristi u različitim granama fizičkih, matematičkih i tehničkih nauka. U praksi izvođenja nastave matematičkog predmeta u srednja škola u skladu s Programom Ministarstva odbrane Ruske Federacije, koncept "apsolutne vrijednosti broja" se ponavlja: u 6. razredu uvodi se definicija modula, njegovo geometrijsko značenje; u 8. razredu se formira pojam apsolutne greške, razmatra se rješenje najjednostavnijih jednačina i nejednačina koje sadrže modul, proučavaju se svojstva aritmetičkog kvadratnog korijena; u 11. razredu koncept se nalazi u rubrici „Koren nstepen." Iskustvo u nastavi pokazuje da učenici često nailaze na poteškoće u rješavanju zadataka koji zahtijevaju poznavanje ovog gradiva, te često preskaču prije nego što počnu sa izradom. U tekstovima ispitnih zadataka za 9. i 11. razred nalaze se i slični zadaci. Osim toga, zahtjevi koje univerziteti nameću maturantima su različiti, odnosno višeg nivoa od zahtjeva školskog kurikuluma. Za život u savremenom društvu veoma je važno formiranje matematičkog stila razmišljanja, koji se manifestuje određenim mentalnim sposobnostima. U procesu rješavanja problema sa modulima potrebna je sposobnost primjene tehnika kao što su generalizacija i konkretizacija, analiza, klasifikacija i sistematizacija, analogija. Rješenje takvih zadataka omogućava vam da provjerite znanje glavnih dijelova školskog kursa, razinu logičkog razmišljanja i početne vještine istraživanja. Ovaj rad je posvećen jednom od odjeljaka - rješavanju jednačina koje sadrže modul. Sastoji se od tri poglavlja. Prvo poglavlje uvodi osnovne pojmove i najvažnije teorijske proračune. Drugo poglavlje predlaže devet osnovnih tipova jednačina koje sadrže modul, razmatra metode za njihovo rješavanje i analizira primjere različitih nivoa složenosti. Treće poglavlje nudi složenije i nestandardne jednačine (trigonometrijske, eksponencijalne, logaritamske i iracionalne). Za svaku vrstu jednačina postoje vježbe za samostalno rješavanje (odgovori i upute su u prilogu). Osnovna svrha ovog rada je pružanje metodičke pomoći nastavnicima u pripremi za nastavu i organizovanju fakultativnih kurseva. Materijal se može koristiti i kao studijski vodič za srednjoškolce. Predloženi zadaci u radu su zanimljivi i nisu uvijek laki za rješavanje, što omogućava osvješćivanje motivacije za učenje učenika, testiranje njihovih sposobnosti i poboljšanje nivoa pripremljenosti maturanata za upis na fakultete. Diferenciran izbor predloženih vežbi podrazumeva prelazak sa reproduktivnog nivoa asimilacije gradiva na kreativni, kao i mogućnost da nauče kako da svoje znanje primene u rešavanju nestandardnih problema.

Poglavlje 1. Uvod.

Odjeljak 1. Određivanje apsolutne vrijednosti .

Definicija : Apsolutna vrijednost (modul) realnog broja a naziva se nenegativnim brojem: a ili -a. Oznaka: │ a │ Unos glasi kako slijedi: “modul broja a” ili “apsolutna vrijednost broja a”

│ a ako je a > 0

│a│ = │ 0 ako je a = 0 (1)

│ - a, ako a
primjeri: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Proširite modul izraza:

a) │x - 8│ ako je x > 12 b) │2x + 3│ ako je x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Odjeljak 2. Osnovna svojstva.

Razmotrimo osnovna svojstva apsolutne vrijednosti. Nekretnina #1: Suprotni brojevi imaju jednake module, tj. │a│=│-a│ Pokažimo ispravnost jednakosti. Zapišimo definiciju broja - a : │- a│= (2) Uporedimo skupove (1) i (2). Očigledno, definicije apsolutnih vrijednosti brojeva a i - a match. shodno tome, │a│=│-a│
Kada razmatramo sljedeća svojstva, ograničavamo se na njihovu formulaciju, budući da je njihov dokaz dat Nekretnina #2: Apsolutna vrijednost sume konačnog broja realni brojevi ne prelazi zbir apsolutnih vrijednosti pojmova: │a 1 + a 2 +…+ a n Nekretnina #3: Apsolutna vrijednost razlike između dva realna broja ne prelazi zbir njihovih apsolutnih vrijednosti: │a - v│ ≤│a│+│v│ Nekretnina #4: Apsolutna vrijednost proizvoda konačnog broja realnih brojeva jednaka je proizvodu apsolutnih vrijednosti faktora: │a · v│=│a│·│v│ Nekretnina #5: Apsolutna vrijednost količnika realnih brojeva jednaka je količniku njihovih apsolutnih vrijednosti:

Odjeljak 3. Geometrijska interpretacija pojma modula broja.

Svaki realan broj može biti povezan sa tačkom na brojevnoj liniji, koja će biti geometrijski prikaz ovog realnog broja. Svaka tačka na brojevnoj pravoj odgovara njenoj udaljenosti od početka, tj. dužina segmenta od početka do date tačke. Ova udaljenost se uvijek smatra nenegativnom vrijednošću. Stoga će dužina odgovarajućeg segmenta biti geometrijska interpretacija apsolutne vrijednosti datog realnog broja

Prikazana geometrijska ilustracija jasno potvrđuje svojstvo broj 1, tj. moduli suprotnih brojeva su jednaki. Odavde se lako razumijeva valjanost jednakosti: │x - a│= │a - x│. Također postaje očiglednije riješiti jednačinu │h│= m, gdje je m ≥ 0, odnosno x 1,2 = ± m. primjeri: 1) │h│= 4 x 1,2 = ± 4 2) │h - 3│= 1
x 1,2 = 2; četiri

Odjeljak 4. Grafikon funkcije y \u003d │h│

Domen ove funkcije su svi realni brojevi.

Odjeljak 5. Simboli.

U budućnosti, kada se razmatraju primjeri rješavanja jednačina, koristit će se sljedeće konvencije: ( - sistemski znak [ - znak postavljanja Prilikom rješavanja sistema jednačina (nejednačina) nalazi se presjek rješenja jednačina (nejednačina) uključenih u sistem. Prilikom rješavanja skupa jednačina (nejednačina) nalazi se unija rješenja jednačina (nejednačina) uključenih u skup.

Poglavlje 2

U ovom poglavlju ćemo pogledati algebarske načine rješavanja jednadžbi koje sadrže jedan ili više modula.

Odjeljak 1. Jednačine oblika │F (h) │= m

Jednačina ovog tipa naziva se najjednostavnija. Ima rješenje ako i samo ako je m ≥ 0. Po definiciji modula, originalna jednadžba je ekvivalentna kombinaciji dvije jednačine: │ F(x)│=m
primjeri:
№1. Riješite jednačinu: │7x - 2│= 9


Odgovor: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odgovor: zbir korijena je - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 označava x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – obe vrednosti zadovoljavaju uslov m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odgovor: broj korijena jednačine 7. vježbe:
№1. Riješite jednačinu i označite zbir korijena: │x - 5│= 3 №2 . Riješite jednadžbu i označite manji korijen: │x 2 + x │ \u003d 0 №3 . Riješite jednadžbu i označite veći korijen: │x 2 - 5x + 4 │ \u003d 4 №4 .Riješi jednačinu i naznači cijeli korijen: │2x 2 - 7x + 6│ \u003d 1 №5 .Riješi jednačinu i naznači broj korijena: │x 4 - 13x 2 + 50 │ = 14

Odjeljak 2. Jednačine oblika F(│h│) = m

Argument funkcije na lijevoj strani je ispod predznaka modula, dok je desna strana nezavisna od varijable. Razmotrimo dva načina rješavanja jednačina ovog tipa. 1 način: Po definiciji apsolutne vrijednosti, originalna jednačina je ekvivalentna ukupnosti dva sistema. U svakom od njih uslov je nametnut izrazu podmodula. F(│h│) =m
Kako je funkcija F(│h│) parna na cijeloj domeni definicije, korijeni jednadžbi F(h) = m i F(-h) = m su parovi suprotnih brojeva. Dakle, dovoljno je riješiti jedan od sistema (kada se primjeri razmatraju na ovaj način, dat će se rješenje jednog sistema). 2 način: Primjena metode uvođenja nove varijable. U ovom slučaju se uvodi oznaka │h│= a, gdje je a ≥ 0. Ova metoda manje obimnog dizajna.
primjeri: №1 . Riješite jednačinu: 3x 2 - 4│x│ = - 1 Koristimo uvođenje nove varijable. Označimo │x│= a, gdje je a ≥ 0. Dobijamo jednačinu 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Vraćamo se na prvobitnu varijablu: │x │ = 1 i │h│= 1/3. Svaka jednadžba ima dva korijena. Odgovor: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Riješite jednačinu: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Nađimo rješenje prvog skupa sistema: 4x 2 + 5x - 2 = 0 D = 57 x 1 = -5 + √57 / 8 x 2 = -5-√57 / 8 Imajte na umu da x 2 ima ne zadovoljava uslov x ≥ 0. Prema rješenju drugi sistem će biti suprotan broj x 1 . Odgovor: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Riješite jednačinu: x 4 - │h│= 0 Označite │h│= a, gdje je a ≥ 0. Dobijamo jednačinu a 4 - a = 0 a (a 3 - 1) = 0 a 1 = 0 a 2 \u003d 1 Vraćamo se na originalnu varijablu: │h│=0 i │h│= 1 x = 0; ± 1 Odgovor: x 1 = 0; X 2 = 1; X 3 = - 1.
vježbe: №6. Riješite jednačinu: 2│h│ - 4,5 = 5 - 3/8 │h│ №7 . Riješite jednačinu, u odgovoru navedite broj korijena: 3x 2 - 7│x│ + 2 = 0 №8 . Riješite jednačinu, u odgovoru navedite cijela rješenja: x 4 + │h│ - 2 = 0

Odjeljak 3. Jednačine oblika │F(h)│ = G(h)

Desna strana jednadžbe ovog tipa ovisi o promjenljivoj i stoga ima rješenje ako i samo ako je desna strana funkcija G(x) ≥ 0. Originalna jednadžba se može riješiti na dva načina: 1 način: Standard, zasnovan na otkrivanju modula na osnovu njegove definicije i sastoji se od ekvivalentnog prelaska na kombinaciju dva sistema. │ F(x)│ =G(X)

Ovu metodu je racionalno koristiti u slučaju složenog izraza za funkciju G(x) i manje složenog izraza za funkciju F(x), budući da bi trebao rješavati nejednačine sa funkcijom F(x). 2 način: Sastoji se u prelasku na ekvivalentni sistem u kojem je uslov nametnut sa desne strane. │ F(x)│= G(x)

Ovu metodu je pogodnije koristiti ako je izraz za funkciju G(x) manje komplikovan nego za funkciju F(x), jer se pretpostavlja rješenje nejednakosti G(x) ≥ 0. Osim toga, u slučaju od nekoliko modula, ova metoda se preporučuje za korištenje druge opcije. primjeri: №1. Riješite jednačinu: │x + 2│= 6 -2x
(1 način) Odgovor: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 smjera) Odgovor: Umnožak korijena je 3.
№3. Riješite jednačinu, u odgovor upišite zbir korijena:
│x - 6 │ \u003d x 2 - 5x + 9

Odgovor: zbir korijena je 4.
vježbe: №9. │x + 4│= - 3x №10. Riješite jednadžbu, u odgovoru navedite broj rješenja: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Riješite jednadžbu, u odgovoru navedite proizvod korijena: │x + 3 │ \u003d x 2 + x - 6

Odjeljak 4. Jednačine oblika │F(x)│= F(x) i │F(x)│= - F(x)

Jednačine ovog tipa se ponekad nazivaju i "lijepe". Pošto desna strana jednadžbe zavisi od varijable, rješenja postoje ako i samo ako je desna strana nenegativna. Prema tome, originalne jednadžbe su ekvivalentne nejednačinama:
│F(x)│= F(x) F(x) ≥ 0 i │F(x)│= - F(x) F(x) primjeri: №1 . Riješite jednačinu, u odgovoru navedite manji cijeli broj korijena: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odgovor: x = 1№2. Riješite jednadžbu, u odgovoru navedite dužinu jaza: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Odgovor: dužina razmaka je 6.№3 . Riješite jednačinu, u odgovoru navedite broj cjelobrojnih rješenja: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Odgovor: 4 cijela rješenja.№4 . Riješite jednačinu, u odgovoru navedite najveći korijen:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 = 0 D = 5 x 1,2 \u003d
≈ 1,4

Odgovor: x = 3.

vježbe: №12. Riješite jednačinu, u odgovoru navedite cijeli korijen: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Riješite jednačinu, u odgovoru navedite broj cjelobrojnih rješenja: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Riješite jednačinu, u odgovoru navedite cijeli broj koji nije korijen jednadžbe:

Odjeljak 5. Jednačine oblika │F(x)│= │G(x)│

Budući da su obje strane jednadžbe nenegativne, rješenje uključuje razmatranje dva slučaja: submodularni izrazi su jednaki ili suprotni po predznaku. Prema tome, originalna jednadžba je ekvivalentna kombinaciji dvije jednadžbe: │ F(x)│= │ G(x)│
primjeri: №1. Riješite jednačinu, u odgovoru navedite cijeli korijen: │x + 3│ \u003d │2x - 1│
Odgovor: cjelobrojni korijen x = 4.№2. Riješite jednačinu: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Odgovor: x = 2.№3 . Riješite jednačinu, u odgovoru navedite proizvod korijena:




Korijeni jednadžbe 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Odgovor: proizvod korijena je 0,25. vježbe: №15 . Riješite jednačinu, u odgovoru navedite cijelo rješenje: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Riješite jednačinu, u odgovoru navedite manji korijen: │5x - 3│=│7 - x│ №17 . Riješite jednačinu, u odgovor upišite zbir korijena:

Odjeljak 6. Primjeri rješavanja nestandardnih jednačina

U ovom dijelu razmatramo primjere nestandardnih jednadžbi, u čijem se rješenju definicijom otkriva apsolutna vrijednost izraza. primjeri:

№1. Riješite jednadžbu, u odgovoru navedite zbir korijena: x │x│- 5x - 6 \u003d 0
Odgovor: zbir korijena je 1 №2. . Riješite jednačinu, u odgovoru navedite manji korijen: x 2 - 4x
- 5 = 0
Odgovor: manji korijen x = - 5. №3. Riješite jednačinu:

Odgovor: x = -1. vježbe: №18. Riješite jednačinu i napišite zbir korijena: x │3x + 5│= 3x 2 + 4x + 3
№19. Riješite jednadžbu: x 2 - 3x \u003d

№20. Riješite jednačinu:

Odjeljak 7. Jednačine oblika │F(x)│+│G(x)│=0

Lako je vidjeti da se na lijevoj strani jednadžbe ovog tipa nalazi zbir nenegativnih veličina. Prema tome, originalna jednadžba ima rješenje ako i samo ako su oba člana istovremeno jednaka nuli. Jednačina je ekvivalentna sistemu jednačina: │ F(x)│+│ G(x)│=0
primjeri: №1 . Riješite jednačinu:
Odgovor: x = 2. №2. Riješite jednačinu: Odgovor: x = 1. vježbe: №21. Riješite jednačinu: №22 . Riješite jednačinu, u odgovor upišite zbir korijena: №23 . Riješite jednačinu, u odgovoru navedite broj rješenja:

Odjeljak 8. Jednačine oblika

Za rješavanje jednadžbi ovog tipa koristi se metoda intervala. Ako se to riješi sekvencijalnim širenjem modula, onda dobivamo n skupova sistema, što je veoma glomazno i ​​nezgodno. Razmotrimo algoritam metode intervala: 1). Pronađite varijabilne vrijednosti X, za koji je svaki modul jednak nuli (nule izraza podmodula):
2). Pronađene vrijednosti su označene brojevnom linijom, koja je podijeljena na intervale (broj intervala, respektivno, jednak je n+1 ) 3). Odredite kojim se znakom svaki modul otkriva u svakom od dobijenih intervala (prilikom rješenja možete koristiti brojevnu pravu, označavajući znakove na njoj) 4). Originalna jednačina je ekvivalentna skupu n+1 sistema, u svakom od kojih je naznačeno pripadnost varijable X jedan od intervala. primjeri: №1 . Riješite jednačinu, u odgovoru navedite najveći korijen:
jedan). Nađimo nule izraza podmodula: x = 2; x = -3 2). Pronađene vrijednosti označavamo na brojevnoj liniji i određujemo kojim se predznakom svaki modul otkriva na dobivenim intervalima:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- nema rješenja Jednačina ima dva korijena. Odgovor: najveći korijen je x = 2. №2. Riješite jednačinu, upišite cijeli korijen u odgovor:
jedan). Nađimo nule izraza podmodula: x = 1.5; x = - 1 2). Pronađene vrijednosti označavamo na brojevnoj liniji i određujemo kojim se predznakom svaki modul otkriva na dobivenim intervalima: x + 1 x + 1 x + 1 - + +
-1 1,5 h 2h – 3 2h – 3 2h – 3 - - +
3).
Poslednji sistem nema rešenja, dakle, jednačina ima dva korena. Prilikom rješavanja jednačine treba obratiti pažnju na znak “-” ispred drugog modula. Odgovor: cjelobrojni korijen x = 7. №3. Riješite jednačinu, u odgovoru navedite zbir korijena: 1). Nađimo nule izraza podmodula: x = 5; x = 1; x = - 2 2). Pronađene vrijednosti označavamo na brojevnoj liniji i određujemo kojim se predznakom svaki modul otkriva na dobivenim intervalima: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Jednačina ima dva korijena x = 0 i 2. Odgovor: zbir korijena je 2. №4 . Riješite jednačinu: 1). Nađimo nule izraza podmodula: x = 1; x = 2; x = 3. 2). Odredimo znak kojim se svaki modul proširuje na dobijenim intervalima. 3).
Kombinirajmo rješenja prvog tri sistema. Odgovor: ; x = 5.
vježbe: №24. Riješite jednačinu:
№25. Riješite jednačinu, u odgovor upišite zbir korijena: №26. Riješite jednačinu, u odgovoru navedite manji korijen: №27. Riješite jednačinu, dajte veći korijen u svom odgovoru:

Odjeljak 9. Jednačine koje sadrže više modula

Jednačine koje sadrže više modula pretpostavljaju prisustvo apsolutnih vrijednosti u izrazima podmodula. Osnovni princip rješavanja jednačina ovog tipa je sekvencijalno otkrivanje modula, počevši od "spoljašnjeg". U toku rješenja koriste se tehnike o kojima se govori u odjeljcima br. 1, br. 3.

primjeri: №1. Riješite jednačinu:
Odgovor: x = 1; - jedanaest. №2. Riješite jednačinu:
Odgovor: x = 0; četiri; - četiri. №3. Riješite jednačinu, u odgovoru navedite proizvod korijena:
Odgovor: Umnožak korijena je 8. №4. Riješite jednačinu:
Označite jednačine stanovništva (1) i (2) i razmotrite rješenje svakog od njih zasebno radi praktičnosti dizajna. Budući da obje jednačine sadrže više od jednog modula, pogodnije je izvršiti ekvivalentan prijelaz na skupove sistema. (1)

(2)


odgovor:
vježbe: №36. Riješite jednadžbu, u odgovoru navedite zbir korijena: 5 │3x-5│ \u003d 25 x №37. Riješite jednačinu, ako postoji više od jednog korijena, u odgovoru navedite zbir korijena: │x + 2│ x - 3x - 10 = 1 №38. Riješite jednačinu: 3 │2x -4│ \u003d 9 │x│ №39. Riješite jednačinu, u odgovoru navedite broj korijena za: 2 │ sin x │ = √2 №40 . Riješite jednačinu, u odgovoru navedite broj korijena:

Odjeljak 3. Logaritamske jednadžbe.

Prije rješavanja sljedećih jednačina potrebno je razmotriti svojstva logaritama i logaritamske funkcije. primjeri: №1. Riješite jednadžbu, u odgovoru navedite proizvod korijena: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

Slučaj 1: ako je x ≥ - 1, onda je log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – zadovoljava uslov x ≥ - 1 2 slučaj: ako je x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – zadovoljava uslov x - 1
Odgovor: Umnožak korijena je 15.
№2. Riješite jednačinu, u odgovoru navedite zbir korijena: lg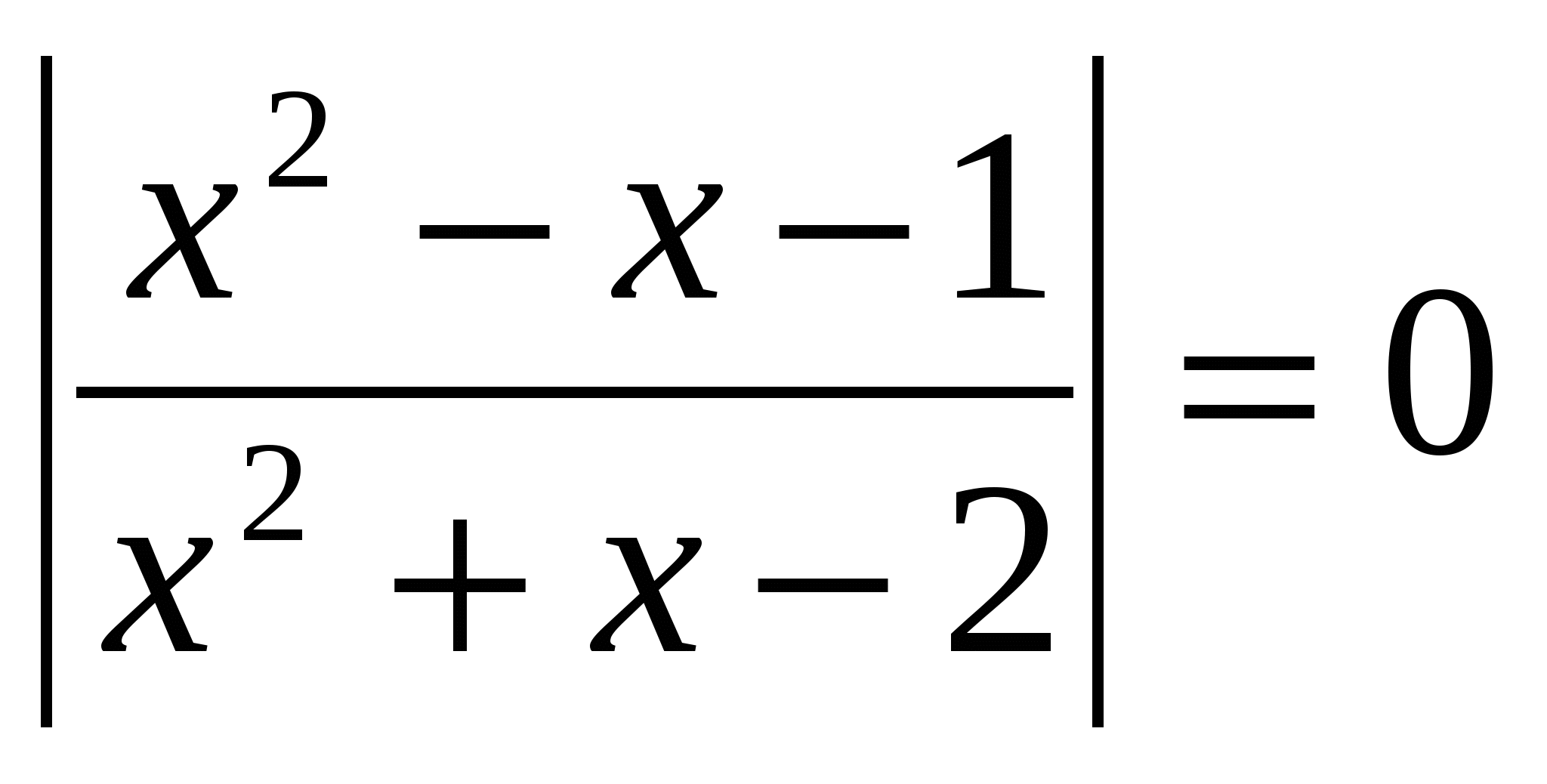
O.D.Z.

Odgovor: zbir korijena je 0,5.
№3. Riješite jednačinu: log 5
O.D.Z.

Odgovor: x = 9. №4. Riješite jednačinu: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Koristimo formulu za prelazak na drugu bazu. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Nađimo nule izraza podmodula: x = 25; x \u003d Ovi brojevi dijele područje dopuštenih vrijednosti na tri intervala, tako da je jednadžba ekvivalentna ukupnosti tri sistema.
Odgovor: )