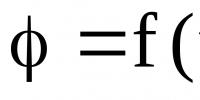CONFÉRENCE №4

LOIS FONDAMENTALES DE LA CINÉTIQUE ET DE LA DYNAMIQUE

MOUVEMENT ROTATIF. MÉCANIQUE

PROPRIÉTÉS DES BIOTISKS. BIOMÉCANIQUE

PROCESSUS DANS LE SYSTÈME LOCOMOTEUR

HUMAIN.

1. Lois fondamentales de la cinématique du mouvement de rotation.

Le mouvement de rotation du corps autour d'un axe fixe est le type de mouvement le plus simple. Il se caractérise par le fait que tous les points du corps décrivent des cercles dont les centres sont situés sur une ligne droite 0 ﺍ 0 ﺍﺍ , appelée axe de rotation (Fig. 1).

Dans ce cas, la position du corps à tout instant est déterminée par l'angle de rotation φ du rayon vecteur R de tout point A par rapport à sa position initiale. Sa dépendance au temps :

(1)

est l'équation du mouvement de rotation. La vitesse de rotation du corps est caractérisée par la vitesse angulaire ω. La vitesse angulaire de tous les points du corps en rotation est la même. C'est une grandeur vectorielle. Ce vecteur est dirigé selon l'axe de rotation et est lié au sens de rotation par la règle de la vis droite :

. (2)

Avec mouvement uniforme d'un point le long d'un cercle

, (3)

où Δφ=2π est l'angle correspondant à une rotation complète du corps, Δt=T est le temps d'une rotation complète, ou la période de rotation. Unité de mesure de vitesse angulaire [ω]=c -1.

Avec un mouvement uniforme, l'accélération du corps est caractérisée par une accélération angulaire ε (son vecteur est situé de manière similaire au vecteur de vitesse angulaire et est dirigé selon celui-ci en accéléré et dans le sens opposé - au ralenti):

. (4)

Unité d'accélération angulaire [ε]=c -2 .

Le mouvement de rotation peut également être caractérisé par la vitesse linéaire et l'accélération de ses points individuels. La longueur de l'arc dS, décrit par tout point A (Fig. 1) lorsqu'il est tourné d'un angle dφ, est déterminé par la formule : dS=Rdφ. (5)

Alors la vitesse linéaire du point :

. (6)

Accélération linéaire un:

. (7)

2. Lois fondamentales de la dynamique des mouvements de rotation.

La rotation du corps autour de l'axe est provoquée par la force F appliquée en tout point du corps, agissant dans un plan perpendiculaire à l'axe de rotation et dirigée (ou ayant une composante dans cette direction) perpendiculairement au rayon vecteur du point d'application (Fig. 1).

Moment de force par rapport au centre de rotation s'appelle une grandeur vectorielle numériquement égale au produit de la force par la longueur de la perpendiculaire d, abaissée du centre de rotation à la direction de la force, appelée bras de la force. Dans la Fig.1 d=R, donc

. (8)

Moment la force de rotation est une grandeur vectorielle. Vecteur attaché au centre du cercle O et dirigé selon l'axe de rotation. direction du vecteur est conforme à la direction de la force selon la règle de la vis droite. Le travail élémentaire dA i , en tournant d'un petit angle dφ, lorsque le corps parcourt un petit chemin dS, est égal à :

Une mesure de l'inertie d'un corps en mouvement de translation est la masse. Lorsqu'un corps tourne, la mesure de son inertie est caractérisée par le moment d'inertie du corps autour de l'axe de rotation.

Le moment d'inertie I i d'un point matériel par rapport à l'axe de rotation est une valeur égale au produit de la masse du point par le carré de sa distance à l'axe (Fig. 2) :

. (10)

Le moment d'inertie du corps autour de l'axe est la somme des moments d'inertie des points matériels qui composent le corps :

. (11)

Soit à la limite (n→∞) :
, (12)

g l'intégration est effectuée sur tout le volume V. De manière similaire, les moments d'inertie de corps homogènes de forme géométrique régulière sont calculés. Le moment d'inertie est exprimé en kg m 2 .

Le moment d'inertie d'une personne par rapport à l'axe de rotation vertical passant par le centre de masse (le centre de masse d'une personne est dans le plan sagittal légèrement en avant de la deuxième vertèbre transversale), selon la position de la personne, a les valeurs suivantes : 1,2 kg m 2 au garde-à-vous ; 17 kg m 2 - en position horizontale.

Lorsqu'un corps tourne, son énergie cinétique est la somme des énergies cinétiques des points individuels du corps :

En différenciant (14), on obtient une variation élémentaire de l'énergie cinétique :

. (15)

En assimilant le travail élémentaire (formule 9) des forces extérieures à la variation élémentaire de l'énergie cinétique (formule 15), on obtient :
, où:
ou considérant que
on a:
. (16)

Cette équation est appelée l'équation de base de la dynamique du mouvement de rotation. Cette dépendance est similaire à la loi II de Newton pour le mouvement de translation.

Le moment cinétique L i d'un point matériel par rapport à l'axe est une valeur égale au produit du moment du point par sa distance à l'axe de rotation :

. (17)

Moment angulaire L d'un corps tournant autour d'un axe fixe :

Le moment cinétique est une grandeur vectorielle orientée selon la direction du vecteur vitesse angulaire.

Revenons maintenant à l'équation principale (16) :

,
.

On porte la valeur constante I sous le signe de la différentielle et on obtient :
, (19)

où Mdt est appelé l'impulsion du moment de force. Si les forces externes n'agissent pas sur le corps (M=0), alors la variation du moment cinétique (dL=0) est également égale à zéro. Cela signifie que le moment cinétique reste constant :
. (20)

Cette conclusion s'appelle la loi de conservation du moment cinétique autour de l'axe de rotation. Il est utilisé, par exemple, pour les mouvements de rotation autour d'un axe libre dans le sport, comme l'acrobatie, etc. Ainsi, un patineur artistique sur glace, en modifiant la position du corps lors de la rotation et, par conséquent, le moment d'inertie par rapport à l'axe de rotation, peut réguler sa vitesse de rotation.

Un corps rigide tournant autour de certains axes passant par le centre de masse, s'il est libéré des influences extérieures, maintient sa rotation indéfiniment. (Cette conclusion est similaire à la première loi de Newton pour le mouvement de translation).

La rotation d'un corps rigide est toujours causée par l'action de forces externes appliquées à des points individuels du corps. Dans ce cas, l'apparition de déformations et l'apparition de forces internes sont inévitables, ce qui dans le cas d'un corps solide assure la conservation pratique de sa forme. Lorsque l'action des forces extérieures cesse, la rotation est conservée : les forces intérieures ne peuvent ni provoquer ni détruire la rotation d'un corps rigide.

Le résultat de l'action d'une force externe sur un corps avec un axe de rotation fixe est un mouvement de rotation accéléré du corps. (Cette conclusion est similaire à la deuxième loi de Newton pour le mouvement de translation).

La loi fondamentale de la dynamique du mouvement de rotation: dans un référentiel inertiel, l'accélération angulaire acquise par un corps tournant autour d'un axe fixe est proportionnelle au moment total de toutes les forces extérieures agissant sur le corps, et inversement proportionnelle au moment d'inertie du corps autour d'un axe donné :

Il est possible de donner une formulation plus simple la loi fondamentale de la dynamique du mouvement de rotation(aussi appelé Deuxième loi de Newton pour le mouvement de rotation): le couple est égal au produit du moment d'inertie et de l'accélération angulaire:

moment cinétique(moment cinétique, moment cinétique) d'un corps est appelé le produit de son moment d'inertie par la vitesse angulaire :

Le moment cinétique est une grandeur vectorielle. Sa direction coïncide avec la direction du vecteur vitesse angulaire.

La variation du moment cinétique est définie comme suit :

. (I.112)

Une modification du moment cinétique (avec un moment d'inertie constant du corps) ne peut se produire qu'à la suite d'une modification de la vitesse angulaire et est toujours due à l'action du moment de force.

Selon la formule, ainsi que les formules (I.110) et (I.112), la variation du moment cinétique peut être représentée par :

. (I.113)

Le produit de la formule (I.113) est appelé moment de force impulsionnel ou moment de conduite. Il est égal à la variation du moment cinétique.

La formule (I.113) est valide à condition que le moment de la force ne change pas avec le temps. Si le moment de la force dépend du temps, c'est-à-dire , alors

. (I.114)

La formule (I.114) montre que : la variation du moment cinétique est égale à l'intégrale temporelle du moment de force. De plus, si cette formule est présentée sous la forme : , alors la définition en découlera instant de force: le moment de force instantané est la dérivée première du moment de quantité de mouvement par rapport au temps,

TRAVAIL DE LABORATOIRE №107

Vérification de l'équation de base de la dynamique

mouvement rotatif

Objectif:Vérification expérimentale de la loi fondamentale de la dynamique du mouvement de rotation à l'aide du pendule d'Oberbeck.

Instruments et accessoires : Pendule Oberbeck avec milliseconde FRM - 15, pied à coulisse.

Introduction théorique

Lorsque l'on considère la rotation d'un corps rigide d'un point de vue dynamique, avec le concept de forces, le concept de moments de forces est introduit, et avec le concept de masse, le concept de moment d'inertie.

Soit un point matériel de masse t sous l'action d'une force extérieure, il se déplace curvilignement par rapport à un point fixe O. Un moment de force agit sur un point matériel et ce point a un moment d'impulsion. La position d'un point matériel en mouvement est déterminée par le vecteur rayon qui lui est tracé à partir du point O (Fig. 1). Le moment de force par rapport à un point fixe O est appelé une quantité vectorielle égale au produit vectoriel du rayon vecteur du vecteur force

Le vecteur est dirigé perpendiculairement au plan des vecteurs et sa direction correspond à la règle de la vis droite. Le module du moment des forces est égal à

où un - angle entre les vecteurs et , h=rsin un - l'épaule de la force, égale à la distance la plus courte du point O à la ligne d'action (le long de laquelle la force agit) de la force.

Le moment cinétique relatif au point O est appelé une quantité vectorielle égale au produit vectoriel du rayon du vecteur par le vecteur moment, c'est-à-dire

Le vecteur est dirigé perpendiculairement au plan des vecteurs et (Fig. 2). Le module du moment cinétique est égal à

où b - l'angle entre la direction des vecteurs et .

La loi fondamentale de la dynamique du mouvement de rotation

Soit le système mécanique constitué de N points matériels sous l'action de forces extérieures, dont la résultante effectue un mouvement curviligne par rapport à un point fixe O, c'est-à-dire

où est le rayon vecteur tiré du point O à jeème point matériel, est le vecteur de la force agissant sur je-ème point matériel.

Vous pouvez également trouver le moment cinétique du système

où est le moment cinétique je-ème point matériel.

Le moment cinétique dépend du temps t car la vitesse est fonction du temps. Prendre la dérivée de la quantité de mouvement du système par rapport au temps t, on a

La formule (7) est une expression mathématique de la loi de base de la dynamique du mouvement de rotation du système, selon laquelle le taux de variation du moment cinétique du système dans le temps est égal au moment résultant des forces externes agissant sur le système.

La loi (7) est également valable pour un corps rigide, puisque un corps rigide peut être considéré comme un ensemble de points matériels.

Soit dans un cas particulier, un corps rigide tourne autour d'un axe fixe passant par le centre de masse, sous l'action d'une force extérieure. Le corps rigide est divisé en points matériels. Pour un point matériel de masse m i l'équation du mouvement s'écrira

Moment angulaire pour je- le point matériel est égal à

Depuis lors de la rotationb = 90 0 , alors la vitesse linéaire est liée à la vitesse angulaire par la formule Alors (9) peut s'écrire

La valeur est le moment d'inertie du point matériel autour de l'axe Z. Alors (10) prend la forme

Compte tenu de (11), la loi de base de la dynamique du mouvement de rotation d'un corps rigide par rapport à un axe fixe s'écrit

où est le moment d'inertie du corps rigide autour de l'axe Z.

À

où est l'accélération angulaire. Selon l'équation principale dynamique du mouvement de rotation (12), le moment résultant de la force externe agissant sur le corps est égal au produit du moment d'inertie J du corps et de son accélération angulaire.

De l'équation (12), il s'ensuit qu'à j = const accélération angulaire du corps

directement proportionnel au moment des forces externes par rapport à l'axe de rotation, c'est-à-dire

À M = constante l'accélération angulaire est inversement proportionnelle au moment d'inertie du corps, c'est-à-dire

Le but de ce travail est de vérifier les relations (13) et (14), et, par conséquent, l'équation de base de la dynamique du mouvement de rotation (12), dont elles sont les conséquences.

Description de la configuration de fonctionnement et de la méthode de mesure

Pour vérifier les relations (13) et (14), on utilise un pendule d'Oberbeck, qui est une roue inertielle en forme de croix. Sur quatre tiges 1 mutuellement perpendiculaires, il y a quatre charges cylindriques identiques 2, qui peuvent être déplacées le long des tiges et fixées à une certaine distance de l'axe. Les charges sont fixées symétriquement, c'est-à-dire de sorte que leur centre de masse coïncide avec l'axe de rotation. Sur l'axe horizontal de la croix se trouve un disque à deux étages 3, sur lequel le fil est enroulé. Une extrémité du fil est fixée au disque, et une charge 4 est suspendue à la deuxième extrémité du fil, sous l'action de laquelle le dispositif est entraîné en rotation. Une vue générale du pendule Oberbeck FRM-06 est illustrée à la Fig.3. Un électro-aimant de freinage est utilisé pour maintenir le système de traverse avec les poids au repos. Afin de lire la hauteur de chute des marchandises, une échelle millimétrique est appliquée sur la colonne 5. Le temps de chute de la charge 4 est mesuré par la montre milliseconde FRM-15, à laquelle les capteurs photoélectriques n ° 1 (6 ) et n° 2 (7) sont connectés. Le capteur photoélectrique n°2 (7) génère une impulsion électrique des mesures de fin de temps et active l'électro-aimant du frein.

Si vous laissez la charge 4 se déplacer, ce mouvement se produira avec une accélération un.

où t- temps de mouvement de la cargaison à partir d'une hauteur h. Dans ce cas, la poulie avec les tiges et les charges situées sur celles-ci tourneront avec une accélération angulairee .

où r- rayon de poulie.

Le couple de la force appliquée à la croix et rapportant l'accélération angulaire de la partie tournante de l'appareil, on le trouve par la formule

où J- la force de tension de la corde. D'après la deuxième loi de Newton pour la charge 4, nous avons

où

où g- Accélération de la gravité.

A partir des formules (12), (15), (16), (17) et (19) nous avons

La procédure d'exécution des travaux et de traitement des résultats de mesure

1. Mesurer le rayon des grandes et petites poulies avec un pied à coulisse r 1 et r 2 .

2. Déterminer la masse de la cargaison 4 en pesant avec précision sur des balances techniques± 0,1g

3. Vérifier la relation (13). Pour ça:

- fixer des masselottes mobiles cylindriques sur les tiges au plus près de l'axe de rotation de manière à ce que la traverse soit dans une position d'équilibre indifférent ;

- enrouler le fil autour d'une poulie à grand rayon r1 et mesurer le temps de déplacement de la cargaison t de haut h montre milliseconde, pourquoi

- connecter le cordon d'alimentation du compteur à l'alimentation ;

- appuyer sur la touche « RÉSEAU » et vérifier si tous les voyants du compteur affichent zéro et si tous les voyants des deux capteurs photoélectriques sont allumés ;

- déplacer le poids vers la position supérieure et vérifier si le circuit est au repos ;

- appuyez sur la touche "START" et mesurez le temps de déplacement de la charge avec une montre milliseconde ;

- appuyer sur la touche « RESET » et vérifier si les relevés des compteurs ont été remis à zéro et si la serrure a été libérée par l'électroaimant ;

- déplacer la charge vers la position supérieure, appuyer sur la touche "START" et vérifier si le circuit n'a pas été bloqué à nouveau ;

- répéter l'expérience 5 fois. Hauteur h il n'est pas recommandé de changer pendant toute l'opération;

- à l'aide des formules (15), (16), (20) calculer les valeurs un 1 , e 1 , M 1 ;

- sans changer l'emplacement des charges mobiles et en laissant ainsi le moment d'inertie du système inchangé, répétez l'expérience en enroulant le fil avec la charge sur une petite poulie avec un rayon r2;

- à l'aide des formules (15), (16), (20) calculer les valeurs un 2 , e 2 , M 2 ;

- vérifier la validité de la conséquence de la loi fondamentale de la dynamique du mouvement de rotation :

, à

- entrer les données des résultats des mesures et des calculs dans les tableaux 1 et 2.

4. Rapport de contrôle (1 quatre). Pour ça:

- poussez jusqu'en butée les masselottes mobiles aux extrémités des tiges, mais de façon que la traverse soit de nouveau dans une position d'équilibre indifférent;

- pour petite poulie r2 déterminer le moment du mouvement de la cargaison t/ selon 5 expériences ;

- à l'aide des formules (15), (20), (21) déterminer les valeurs un / , e / , J1;

- lors de la vérification du rapport quand vous pouvez utiliser les valeurs de l'expérience précédente en définissant et ;

- à l'aide de la formule (21) déterminer la valeur J 2 ;

- calculer les valeurs de et .

- Enregistrez les résultats des mesures et des calculs dans le tableau 3.

Tableau 1

r1	m	h	t 1	< t 1 >	un 1	e 1	M 1
	kg				m/s 2	à partir de -2	H × m

Tableau 2

r2	t 2	< t 2 >	un 2	e 2	M 2	M 1 /M 2	e 1 / e 2
			m/s 2	à partir de -2	H × m

Tableau 3

r 2	t /	< t / >	un /	e /	J 1	un //	J 2	e //	e / / e //	J 2 / J 1
			m/s 2	à partir de -2	kg × m 2	m/s 2	kg × m 2	à partir de -2

Questions pour l'admission au travail

1. Quel est le but du travail ?

2. Formuler la loi fondamentale de la dynamique du mouvement de rotation. Expliquez la signification physique des grandeurs incluses dans cette loi, indiquez les unités de leur mesure en "SI".

3. Décrire le dispositif de l'installation de travail.

Questions pour protéger l'œuvre

1. Donner les définitions du moment des forces, moment d'impulsion d'un point matériel par rapport à un point fixe O.

2. Formuler la loi de base de la dynamique du mouvement de rotation d'un corps rigide par rapport à un point fixe O et à un axe fixe Z.

3. Définir le moment d'inertie d'un point matériel et d'un corps rigide.

4. Déduire des formules de travail.

5. Déduire le rapport pour et pour

6. Y a-t-il des critiques à ce travail ?

L'instant de puissance

L'action rotative d'une force est déterminée par sa quantité de mouvement. Le moment de force autour d'un point est le produit croisé

Vecteur de rayon tracé d'un point à un autre d'application de la force (Fig. 2.12). Unité de mesure du moment de force.

Graphique 2.12

La grandeur du moment de force

ou tu peux écrire

où est l'épaule de la force (la distance la plus courte entre le point et la ligne d'action de la force).

La direction du vecteur est déterminée par la règle du produit vectoriel ou par la règle de la "vis droite" (on combine les vecteurs et la translation parallèle au point O, la direction du vecteur est déterminée de sorte que de son extrémité la tourner du vecteur à est visible dans le sens antihoraire - sur la Fig. 2.12, le vecteur est dirigé perpendiculairement au plan "de nous" (de même, selon la règle de la vrille - le mouvement de translation correspond à la direction du vecteur, la rotation correspond à un tour de à)).

Le moment d'une force autour d'un point est nul si la ligne d'action de la force passe par ce point.

La projection d'un vecteur sur n'importe quel axe, par exemple l'axe z, est appelée moment de force autour de cet axe. Pour déterminer le moment de la force autour de l'axe, projetez d'abord la force sur un plan perpendiculaire à l'axe (Fig. 2.13), puis trouvez le moment de cette projection par rapport au point d'intersection de l'axe avec le plan qui lui est perpendiculaire . Si la ligne d'action de la force est parallèle à l'axe ou le traverse, alors le moment de la force autour de cet axe est égal à zéro.

Illustration 2.13

moment cinétique

Moment d'élan point matériel une masse se déplaçant à une vitesse relative à n'importe quel point de référence s'appelle un produit vectoriel

Le rayon vecteur d'un point matériel (Fig. 2.14) est sa quantité de mouvement.

Illustration 2.14

La valeur du moment cinétique du point matériel

où est la distance la plus courte entre la ligne vectorielle et le point .

La direction du moment cinétique est déterminée de la même manière que la direction du moment de force.

Si l'expression de L 0 est multipliée et divisée par l, on obtient :

Où - le moment d'inertie d'un point matériel - un analogue de la masse en mouvement de rotation.

Vitesse angulaire.

Moment d'inertie d'un corps rigide

On peut voir que les formules résultantes sont très similaires aux expressions de la quantité de mouvement et de la deuxième loi de Newton, respectivement, seulement au lieu de la vitesse et de l'accélération linéaires, la vitesse et l'accélération angulaires sont utilisées, et au lieu de la masse, la quantité Je=mR 2, appelé moment d'inertie d'un point matériel .

Si le corps ne peut pas être considéré comme un point matériel, mais peut être considéré comme absolument rigide, alors son moment d'inertie peut être considéré comme la somme des moments d'inertie de ses parties infiniment petites, puisque les vitesses angulaires de rotation de ces parties sont les mêmes (Fig. 2.16). La somme des infinitésimaux est l'intégrale :

Pour tout corps, il existe des axes passant par son centre d'inertie, qui ont la propriété suivante : lorsque le corps tourne autour de tels axes en l'absence d'influences extérieures, les axes de rotation ne changent pas de position. Ces axes sont appelés axes libres du corps . On peut prouver que pour un corps de forme quelconque et avec une distribution de densité quelconque, il existe trois axes libres mutuellement perpendiculaires, appelés axes principaux d'inertie corps. Les moments d'inertie d'un corps autour des axes principaux sont appelés moments d'inertie principaux (intrinsèques) corps.

Les principaux moments d'inertie de certains corps sont donnés dans le tableau:

Théorème de Huygens-Steiner.

Cette expression est appelée Théorèmes de Huygens-Steiner : le moment d'inertie du corps autour d'un axe arbitraire est égal à la somme du moment d'inertie du corps autour d'un axe parallèle à celui donné et passant par le centre de masse du corps, et du produit de la masse par le carré de la distance entre les axes.

L'équation de base de la dynamique du mouvement de rotation

La loi de base de la dynamique du mouvement de rotation peut être obtenue à partir de la deuxième loi de Newton pour le mouvement de translation d'un corps rigide

Où F est la force appliquée au corps par la masse m; un est l'accélération linéaire du corps.

Si à un corps de masse rigide m au point A (Fig. 2.15) appliquer une force F, alors par suite d'une liaison rigide entre tous les points matériels du corps, tous recevront une accélération angulaire ε et les accélérations linéaires correspondantes, comme si une force F 1 …F n agissait sur chaque point. Pour chaque point matériel, vous pouvez écrire :

Où donc

Où moi je- lester je-ème point ; ε est l'accélération angulaire ; r je est sa distance à l'axe de rotation.

En multipliant les côtés gauche et droit de l'équation par r je, on a

Où - le moment de force - est le produit de la force sur son épaule.

Riz. 2.15. Corps rigide tournant sous l'action d'une force F autour de l'axe "ОО"

- moment d'inertie jeème point matériel (analogue à la masse en mouvement de rotation).

L'expression peut s'écrire ainsi :

Résumons les parties gauche et droite sur tous les points du corps :

L'équation est la loi fondamentale de la dynamique du mouvement de rotation d'un corps rigide. Valeur - la somme géométrique de tous les moments de forces, c'est-à-dire le moment de force F, donnant une accélération ε à tous les points du corps. est la somme algébrique des moments d'inertie de tous les points du corps. La loi est formulée comme suit : "Le moment de force agissant sur un corps en rotation est égal au produit du moment d'inertie du corps et de l'accélération angulaire."

D'autre part

À son tour - un changement dans le moment cinétique du corps.

Alors la loi fondamentale de la dynamique du mouvement de rotation peut être réécrite comme suit :

Ou - l'impulsion du moment de force, agissant sur un corps en rotation, est égale à la variation de son moment cinétique.

Loi de conservation du moment cinétique

Semblable à ZSI.

Selon l'équation de base de la dynamique du mouvement de rotation, le moment de force autour de l'axe Z : . Par conséquent, dans un système fermé et, par conséquent, le moment cinétique total autour de l'axe Z de tous les corps inclus dans un système fermé est une valeur constante. Il exprime loi de conservation du moment cinétique . Cette loi n'est valable que dans les référentiels inertiels.

Faisons une analogie entre les caractéristiques du mouvement de translation et du mouvement de rotation.

Bases et fondations sont calculées selon 2 états limites

	Par capacité portante :	N- la charge de conception spécifiée sur la base dans la combinaison la plus défavorable ; - capacité portante (charge ultime) de la fondation pour une direction de charge donnée N; - coefficient des conditions de travail de la fondation (<1); - коэффициент надежности (>1).
	Selon les déformations limites :	- tassement absolu calculé de la fondation; - différence relative calculée des tassements de fondation ; , - valeurs limites, respectivement, de la différence absolue et relative des tassements de fondation (SNiP 2.02.01-83 *)

Dynamique de rotation

Avant-propos

J'attire l'attention des élèves sur le fait que CE matériel n'était pas ABSOLUMENT considéré à l'école (sauf pour la notion de moment de force).

1. La loi de la dynamique du mouvement de rotation

un. Loi de la dynamique du mouvement de rotation

b. L'instant de pouvoir

c. Moment d'une paire de forces

ré. Moment d'inertie

2. Moments d'inertie de certains corps :

un. Anneau (cylindre à paroi mince)

b. Cylindre à paroi épaisse

c. cylindre solide

e. tige mince

3. Théorème de Steiner

4. Moment angulaire du corps. Modification du moment cinétique du corps. impulsion d'élan. Loi de conservation du moment cinétique

5. Fonctionnement rotatif

6. Énergie cinétique de rotation

7. Comparaison des quantités et des lois pour les mouvements de translation et de rotation

1a. Considérons un corps rigide pouvant tourner autour d'un axe fixe OO (Fig. 3.1). Décomposons ce corps solide en masses élémentaires distinctes Δ m je . La résultante de toutes les forces appliquées à Δ m je , noté par . Il suffit de considérer le cas où la force se trouve dans un plan perpendiculaire à l'axe de rotation : les composantes de force parallèles à l'axe ne peuvent pas affecter la rotation du corps, puisque l'axe est fixe. Alors l'équation de la deuxième loi de Newton pour les composantes tangentielles de la force et de l'accélération s'écrira :

La composante normale de la force fournit une accélération centripète et n'affecte pas l'accélération angulaire. D'après (1.27) : , où est le rayon de rotation je- ce point. Alors

Multiplions les deux côtés de (3.2) par :

remarquerez que

où α est l'angle entre le vecteur force et le vecteur rayon du point (Fig. 3.1), est la perpendiculaire abaissée à la ligne d'action de la force à partir du centre de rotation (épaulement de la force). Introduisons le concept de moment de force.

1b. Moment de force par rapport à l'axe est appelé un vecteur dirigé selon l'axe de rotation et associé à la direction de la force par la règle vrille dont le module est égal au produit de la force par son bras : . Épaule de force je par rapport à l'axe de rotation est la distance la plus courte entre la ligne d'action de la force et l'axe de rotation. Dimension du moment de force :

Sous forme vectorielle, le moment de force autour d'un point :

Le vecteur du moment de force est perpendiculaire à la fois à la force et au rayon vecteur du point de son application :

Si le vecteur de force est perpendiculaire à l'axe, alors le vecteur du moment de force est dirigé le long de l'axe selon la règle de la vis droite, et l'amplitude du moment de force par rapport à cet axe (projection sur l'axe) est déterminé par la formule (3.4) :

Le moment de la force dépend à la fois de l'amplitude de la force et du bras de la force. Si la force est parallèle à l'axe, alors .

1c. Couple de puissance - ce sont deux forces égales en amplitude et opposées en direction, dont les lignes d'action ne coïncident pas (Fig. 3.2). Le bras d'une paire de forces est la distance entre les lignes d'action des forces. Trouvons le moment total du couple de forces et () dans la projection sur l'axe passant par le point O :

C'est-à-dire que le moment d'une paire de forces est égal au produit de l'amplitude de la force et du plccho de la paire :

Revenons à (3.3). En tenant compte de (3.4) et (3.6) :

1d. Définition : une valeur scalaire égale au produit de la masse d'un point matériel par le carré de sa distance à l'axe est appelée moment d'inertie d'un point matériel par rapport à l'axe OO :

Dimension du moment d'inertie

Les vecteurs et coïncident en direction avec l'axe de rotation, sont liés au sens de rotation selon la règle de la vrille, donc l'égalité (3.9) peut être réécrite sous forme vectorielle :

Soit (3.10) sur toutes les masses élémentaires en lesquelles le corps est divisé :

Ici, il est pris en compte que l'accélération angulaire de tous les points d'un corps rigide est la même, et elle peut être retirée du signe somme. Sur le côté gauche de l'équation se trouve la somme des moments de toutes les forces (tant externes qu'internes) appliquées à chaque point du corps. Mais selon la troisième loi de Newton, les forces avec lesquelles les points du corps interagissent les uns avec les autres (forces internes) sont égales en amplitude et opposées en direction et se trouvent sur la même ligne droite, de sorte que leurs moments s'annulent. Ainsi, dans la partie gauche de (3.11) le moment total des seules forces externes reste : .

La somme des produits des masses élémentaires et le carré de leurs distances à l'axe de rotation s'appelle moment d'inertie d'un corps rigide sur cet axe :

De cette façon, ; - c'est la loi fondamentale de la dynamique du mouvement de rotation d'un corps rigide (analogue à la seconde loi de Newton) : l'accélération angulaire d'un corps est directement proportionnelle au moment total des forces externes et inversement proportionnelle au moment d'inertie du corps :

Moment d'inertie jesolide est une mesure des propriétés inertes d'un corps solide pendant un mouvement de rotation et est similaire à la masse d'un corps dans la deuxième loi de Newton. Elle dépend essentiellement non seulement de la masse du corps, mais aussi de sa répartition par rapport à l'axe de rotation (dans la direction perpendiculaire à l'axe).

Dans le cas d'une distribution continue de masse, la somme en (3.12) se réduit à une intégrale sur tout le volume du corps :

2a. Moment d'inertie d'un anneau mince autour d'un axe passant par son centre perpendiculairement au plan de l'anneau.

puisque pour tout élément de l'anneau sa distance à l'axe est la même et égale au rayon de l'anneau : .

2b. Cylindre à paroi épaisse (disque) avec rayon intérieur et rayon extérieur .

Calculons le moment d'inertie d'un disque homogène de densité ρ , la taille h, rayon intérieur et rayon extérieur (Fig.3.3) par rapport à l'axe passant par le centre de masse perpendiculaire au plan du disque. Divisons le disque en anneaux minces d'épaisseur et de hauteur de sorte que le rayon intérieur de l'anneau soit , et l'extérieur soit . Le volume d'un tel anneau est , où est l'aire de la base de l'anneau fin. Sa masse :

On substitue dans (3.14) et on intègre sur r():

Masse du disque, puis enfin :

2c. Cylindre plein (disque).

Dans le cas particulier d'un disque ou d'un cylindre plein de rayon R substituons dans (3.17) R 1 =0, R 2 =R et obtenir:

Moment d'inertie d'une boule de rayon R et la masse relative à l'axe passant par son centre (Fig. 3.4), est (sans preuve) :

2e. Le moment d'inertie d'une tige mince avec masse et longueur par rapport à l'axe passant par son extrémité perpendiculaire à la tige (Fig. 3.5).

Nous divisons la tige en segments de longueur infiniment petits. La masse d'une telle zone. Substituer dans (3.14) et intégrer de 0 à :

Si l'axe passe par le centre de la tige perpendiculairement à celle-ci, on peut calculer le moment d'inertie de la moitié de la tige à l'aide de (3.20) puis doubler :

3. Si l'axe de rotation ne passe pas passant par le centre de masse du corps (Fig.3.6), les calculs utilisant la formule (3.14) peuvent être assez compliqués. Dans ce cas, le calcul du moment d'inertie est facilité en utilisant Théorèmes de Steiner : le moment d'inertie du corps autour d'un axe quelconque est égal à la somme des moments d'inertie je c corps autour d'un axe passant par le centre de masse du corps parallèle à cet axe, et le produit de la masse corporelle par le carré de la distance entre essieux :

Voyons comment fonctionne le théorème de Steiner si nous l'appliquons à une tige :

Il est facile de voir qu'une identité est obtenue puisque dans ce cas la distance entre les axes est égale à la moitié de la longueur de la tige.

4. Moment angulaire du corps. Modification du moment cinétique du corps. impulsion d'élan. Loi de conservation du moment cinétique.

De la loi de la dynamique du mouvement de rotation et de la définition de l'accélération angulaire, il s'ensuit :

Si donc . Introduisons le moment cinétique du corps rigide comme

La relation (3.24) est la loi de base de la dynamique des corps rigides pour le mouvement de rotation. Il peut être réécrit comme ceci :

puis ce sera un analogue de la deuxième loi de Newton pour le mouvement de translation sous forme impulsive (2.5)

L'expression (3.24) peut être intégrée :

et formuler la loi de variation du moment cinétique : la variation du moment d'impulsion du corps est égale à l'impulsion du moment total des forces externes . La quantité est appelée l'impulsion du moment de force et est similaire à l'impulsion de la force dans la formulation de la deuxième loi de Newton pour le mouvement de translation (2.2) ; le moment cinétique est analogue à la quantité de mouvement.

Dimension du moment cinétique

Le moment cinétique d'un corps rigide autour de son axe de rotation est un vecteur dirigé le long de l'axe de rotation selon la règle de la vrille.

Le moment cinétique d'un point matériel par rapport au point O (Fig. 3.6) est :

où est le rayon vecteur d'un point matériel, est sa quantité de mouvement. Le vecteur de moment cinétique est dirigé selon la règle de la vrille perpendiculaire au plan dans lequel se trouvent les vecteurs et: sur la Fig. 3.7 - à nous à cause de la figure. La grandeur du moment cinétique

Nous divisons un corps rigide tournant autour d'un axe en masses élémentaires et additionnons le moment cinétique de chaque masse sur tout le corps (le même peut être écrit comme une intégrale, ce n'est pas fondamental):

Puisque la vitesse angulaire de tous les points est la même et est dirigée le long de l'axe de rotation, elle peut s'écrire sous forme vectorielle :

Ainsi, l'équivalence des définitions (3.23) et (3.26) est prouvée.

Si le moment total des forces externes est nul, alors le moment cinétique du système ne change pas(voir 3.25):

. C'est la loi de conservation de la quantité de mouvement . Ceci est possible lorsque :

a) le système est fermé (ou) ;

b) les forces externes n'ont pas de composantes tangentielles (le vecteur force passe par l'axe/centre de rotation) ;

c) les forces externes sont parallèles à l'axe de rotation fixe.

Exemples d'utilisation/fonctionnement de la loi de conservation du moment cinétique :

1. gyroscope ;

2. Banc de Joukovski;

3. patineur sur glace.

5. Travailler avec un mouvement rotatif.

Soit le corps tourne d'un angle sous l'action d'une force et l'angle entre le déplacement et la force est ; - le rayon vecteur du point d'application de la force (Fig. 3.8), alors le travail de la force est égal à :