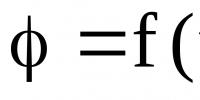Liniile de trecere sunt ușor de recunoscut după astfel de semne. Semnul 1. Dacă există patru puncte pe două drepte care nu se află în același plan, atunci aceste drepte se intersectează (Fig. 1.21).

Într-adevăr, dacă dreptele date s-ar intersecta sau ar fi paralele, atunci ele s-ar afla în același plan și atunci punctele date s-ar afla în același plan, ceea ce contrazice condiția.

Semnul 2. Dacă linia O se află în plan, iar linia b intersectează planul a la un moment dat

M nu se află pe linia a, apoi liniile a și b se intersectează (fig. 1.22).

Într-adevăr, luând oricare două puncte de pe dreapta a și oricare două puncte de pe dreapta b, ajungem la criteriul 1, adică. a și b se intersectează.

Exemple reale de linii de intersectare sunt oferite de nodurile rutiere (Fig. 1.23).

În spațiu, există mai multe perechi de drepte care se intersectează, într-un anumit sens, decât perechi de drepte paralele sau care se intersectează. Acest lucru poate fi explicat după cum urmează.

Să luăm în spațiu un punct A și o dreaptă a care nu trece prin punctul A. Pentru a trasa o dreaptă paralelă cu dreapta a prin punctul A, este necesar să trasăm planul a prin punctul A și dreapta a ( Propunerea 2 din Secțiunea 1.1), apoi în plan și trasați o dreaptă b paralelă cu dreapta a (Fig. 1.24).

Există o singură astfel de linie b. Toate dreptele care trec prin punctul A și care intersectează dreapta O se află și ele în planul a și îl umplu pe tot, cu excepția dreptei b. Toate celelalte drepte care trec prin A și umplu tot spațiul, cu excepția planului a, se vor intersecta cu dreapta a. Se poate spune că liniile care se intersectează în spațiu sunt un caz general, iar liniile care se intersectează și paralele sunt cazuri speciale. „Micile perturbații” ale liniilor oblice le lasă înclinate. Dar proprietățile de a fi paralel sau de a se intersecta cu „mici perturbații” în spațiu nu sunt păstrate.

În mai puțin de un minut, am creat un nou fișier Verdov și am continuat cu un subiect atât de interesant. Trebuie să surprindeți momentele stării de spirit de lucru, așa că nu va exista nicio introducere lirică. Va fi bătaie prozaică =)

Cele două spații drepte pot:

1) se încrucișează;

2) se intersectează în punctul ;

3) să fie paralel;

4) potrivire.

Cazul #1 este fundamental diferit de celelalte cazuri. Două drepte se intersectează dacă nu se află în același plan.. Ridicați un braț în sus și întindeți celălalt braț înainte - iată un exemplu de linii care se intersectează. În punctele 2-4, liniile se află în mod necesar într-un singur plan.

Cum se află poziția relativă a liniilor în spațiu?

Luați în considerare două spații drepte:

- Drept, punctși vector de direcție;
este o dreaptă definită de un punct și un vector de direcție.

Pentru o mai bună înțelegere, să facem un desen schematic:

Desenul prezintă linii oblice ca exemplu.

Cum să te descurci cu aceste rânduri?

Deoarece punctele sunt cunoscute, este ușor să găsiți vectorul.

Dacă drept se încrucișează, apoi vectorii nu coplanare(vezi lecția Dependența liniară (non) a vectorilor. Baza vectorială), ceea ce înseamnă că determinantul compus din coordonatele lor este diferit de zero. Sau, care este de fapt același, va fi diferit de zero: .

În cazurile nr. 2-4, construcția noastră „cade” într-un singur plan, în timp ce vectorii coplanare, A produs mixt vectori dependenți liniar este egal cu zero: .

Am extins algoritmul în continuare. Să ne prefacem că , prin urmare, liniile fie se intersectează, fie sunt paralele, fie coincid.

Dacă vectorii de direcţie coliniare, atunci liniile sunt fie paralele, fie coincid. Ca final, propun următoarea tehnică: luăm orice punct al unei drepte și înlocuim coordonatele acestuia în ecuația celei de-a doua drepte; dacă coordonatele „s-au apropiat”, atunci liniile coincid, dacă „nu s-au apropiat”, atunci liniile sunt paralele.

Cursul algoritmului este nepretențios, dar exemplele practice încă nu interferează:

Exemplul 11

Aflați poziția relativă a două drepte

Soluţie: ca și în multe probleme de geometrie, este convenabil să aranjați soluția punct cu punct:

1) Extragem puncte și vectori direcție din ecuații:

2) Găsiți vectorul:

Astfel, vectorii sunt coplanari, ceea ce înseamnă că dreptele se află în același plan și se pot intersecta, fi paralele sau coincide.

4) Verificați coliniaritatea vectorilor de direcție.

Să compunem un sistem din coordonatele corespunzătoare acestor vectori:

Din toata lumea Ecuația implică că, prin urmare, sistemul este consistent, coordonatele corespunzătoare ale vectorilor sunt proporționale, iar vectorii sunt coliniari.

Concluzie: liniile sunt paralele sau coincid.

5) Aflați dacă liniile au puncte comune. Să luăm un punct aparținând primei drepte și să înlocuim coordonatele acestuia în ecuațiile dreptei:

Astfel, liniile nu au puncte comune și nu le mai rămâne nimic decât să fie paralele.

Răspuns:

Un exemplu interesant pentru solutie independenta:

Exemplul 12

Aflați poziția relativă a liniilor

Acesta este un exemplu de do-it-yourself. Rețineți că a doua linie are litera ca parametru. Logic. În cazul general, acestea sunt două linii diferite, deci fiecare linie are propriul parametru.

Și, din nou, vă îndemn să nu săriți peste exemple, voi scăpa sarcinile pe care le propun sunt departe de a fi aleatorii ;-)

Probleme cu o linie dreaptă în spațiu

În partea finală a lecției, voi încerca să iau în considerare numărul maxim de probleme diferite cu linii spațiale. În acest caz, se va respecta ordinea începută a narațiunii: mai întâi vom lua în considerare problemele cu liniile care se intersectează, apoi cu liniile care se intersectează, iar la final vom vorbi despre liniile paralele în spațiu. Totuși, trebuie să spun că unele dintre sarcinile acestei lecții pot fi formulate pentru mai multe cazuri de linii drepte deodată și, în acest sens, împărțirea secțiunii în paragrafe este oarecum arbitrară. Sunt exemple mai simple, sunt mai multe exemple complexeși sperăm că fiecare va găsi ceea ce are nevoie.

Liniile încrucișate

Vă reamintesc că liniile se intersectează dacă nu există un plan în care să se afle ambele. Când mă gândeam la practică, mi-a venit în minte o sarcină monstruoasă, iar acum mă bucur să vă prezint atenției un dragon cu patru capete:

Exemplul 13

Sunt date linii drepte. Necesar:

a) să demonstreze că liniile se intersectează;

b) găsiți ecuațiile dreptei care trece prin punctul perpendicular pe dreptele date;

c) alcătuiţi ecuaţiile unei drepte care conţine perpendiculară comună linii de intersectare;

d) aflați distanța dintre linii.

Soluţie: Drumul va fi stăpânit de cel plimbat:

a) Să demonstrăm că dreptele se intersectează. Să găsim punctele și vectorii direcție ai acestor drepte:

Să găsim vectorul:

Calcula produs mixt al vectorilor:

Deci vectorii nu coplanare, ceea ce înseamnă că liniile se intersectează, ceea ce urma să fie demonstrat.

Probabil, toată lumea a observat de mult că pentru liniile oblice, algoritmul de verificare se dovedește a fi cel mai scurt.

b) Să aflăm ecuațiile dreptei care trece prin punctul și este perpendiculară pe drepte. Să facem un desen schematic:

Pentru varietate, am postat un direct PE linii drepte, vezi cum se șterge ușor la punctele de trecere. Încrucișări? Da, în cazul general, linia „de” se va intersecta cu liniile originale. Deși nu ne interesează acest moment, trebuie doar să construim o linie perpendiculară și atât.

Ce se știe despre „de” direct? Punctul care îi aparține este cunoscut. Lipsește vectorul direcție.

Prin condiție, linia trebuie să fie perpendiculară pe linii, ceea ce înseamnă că vectorul său de direcție va fi ortogonal cu vectorii de direcție. Motivul deja familiar din Exemplul nr. 9, să găsim produsul vectorial:

Să compunem ecuațiile dreptei „de” după punct și vectorul de direcție:

Gata. În principiu, se pot schimba semnele la numitori și se pot scrie răspunsul în formă , dar nu este nevoie de asta.

Pentru a verifica, este necesar să înlocuiți coordonatele punctului în ecuațiile obținute ale dreptei, apoi folosind produs scalar al vectorilor asigurați-vă că vectorul este într-adevăr ortogonal cu vectorii de direcție „pe unu” și „pe doi”.

Cum se găsesc ecuațiile unei drepte care conține o perpendiculară comună?

c) Această problemă este mai dificilă. Recomand ca nenorocilor să sară peste acest paragraf, nu vreau să vă răcesc simpatia sinceră pentru geometria analitică =) Apropo, ar putea fi mai bine ca și cititorii mai pregătiți să aștepte, adevărul este că complexitatea exemplului ar trebui să fie pus ultimul în articol, dar conform logicii prezentării ar trebui să fie localizat aici.

Deci, este necesar să se găsească ecuațiile dreptei, care conține perpendiculara comună a liniilor oblice.

este un segment de dreaptă care leagă dreptele date și este perpendicular pe liniile date:

Iată bărbatul nostru frumos: - perpendiculară comună a liniilor care se intersectează. El este singurul. Nu există altul ca acesta. De asemenea, trebuie să compunem ecuațiile unei linii drepte care conține un segment dat.

Ce se știe despre „uh” direct? Este cunoscut vectorul său de direcție, găsit în paragraful anterior. Dar, din păcate, nu cunoaștem un singur punct care să aparțină dreptei „em”, nu cunoaștem capetele perpendicularei - puncte. Unde intersectează această dreaptă perpendiculară cele două drepte originale? Africa, Antarctica? Din revizuirea și analiza inițială a stării, nu este deloc clar cum se rezolvă problema .... Dar există o mișcare dificilă asociată cu utilizarea ecuațiilor parametrice ale unei linii drepte.

Să luăm o decizie punct cu punct:

1) Să rescriem ecuațiile primei drepte în formă parametrică:

Să luăm în considerare un punct. Nu știm coordonatele. DAR. Dacă un punct aparține unei linii date, atunci coordonatele acestuia corespund cu , notați-l cu . Apoi coordonatele punctului vor fi scrise ca:

Viața devine din ce în ce mai bună, o necunoscută - până la urmă, nu trei necunoscute.

2) Aceeași ultraj trebuie făcută și asupra celui de-al doilea punct. Să rescriem ecuațiile celei de-a doua drepte în formă parametrică:

Dacă un punct aparține unei linii date, atunci cu un sens foarte specific coordonatele sale trebuie să satisfacă ecuațiile parametrice:

Sau:

3) Vectorul , ca și vectorul găsit anterior , va fi vectorul de direcție al dreptei . Cum se compune un vector din două puncte a fost luat în considerare în timpuri imemoriale în lecție Vectori pentru manechine. Acum diferența este că coordonatele vectorilor sunt scrise cu valori ale parametrilor necunoscute. Şi ce dacă? Nimeni nu interzice scăderea coordonatele corespunzătoare ale începutului vectorului din coordonatele sfârșitului vectorului.

Există două puncte: .

Găsirea unui vector:

4) Deoarece vectorii de direcție sunt coliniari, atunci un vector este exprimat liniar prin celălalt cu un coeficient de proporționalitate „lambda”:

Sau în coordonate:

S-a dovedit a fi cel mai obișnuit sistem de ecuații liniare cu trei necunoscute, care este solubil standard, de exemplu, metoda lui Cramer. Dar aici există o oportunitate de a scăpa cu puțin sânge, din a treia ecuație vom exprima „lambda” și o vom înlocui în prima și a doua ecuație:

În acest fel: , iar „lambda” nu avem nevoie. Faptul că valorile parametrilor s-au dovedit a fi aceleași este pură întâmplare.

5) Cerul se limpezește complet, înlocuiți valorile găsite către locațiile noastre:

Vectorul direcție nu este deosebit de necesar, deoarece omologul său a fost deja găsit.

După o călătorie lungă, este întotdeauna interesant să efectuați o verificare.

:

Se obțin egalitățile corecte.

Înlocuiți coordonatele punctului în ecuații :

Se obțin egalitățile corecte.

6) Coarda finală: vom compune ecuațiile unei drepte pentru un punct (puteți lua) și un vector de direcție:

În principiu, puteți ridica un punct „bun” cu coordonate întregi, dar acest lucru este cosmetic.

Cum să găsiți distanța dintre liniile care se intersectează?

d) Tăiem al patrulea cap al dragonului.

Metoda unu. Nici măcar un mod, ci un mic caz special. Distanța dintre liniile care se intersectează este egală cu lungimea perpendicularei lor comune: .

Punctele extreme ale perpendicularei comune găsite în paragraful anterior, iar sarcina este elementară:

Metoda a doua. În practică, cel mai adesea capetele perpendicularei comune sunt necunoscute, așa că se folosește o abordare diferită. Este posibil să se deseneze plane paralele prin două drepte care se intersectează, iar distanța dintre planurile date este egală cu distanța dintre liniile date. În special, o perpendiculară comună iese între aceste planuri.

În cursul geometriei analitice, din considerentele de mai sus, a fost derivată o formulă pentru găsirea distanței dintre liniile oblice:
(în loc de punctele noastre „em unu, doi” putem lua puncte arbitrare ale liniilor).

Produs mixt al vectorilor găsit deja în paragraful „a”: .

Produsul încrucișat al vectorilor găsit în paragraful „fi”: , calculează-i lungimea:

În acest fel:

Așează cu mândrie trofeele pe un rând:

Răspuns:
A) , prin urmare, liniile se intersectează, ceea ce se cerea a fi demonstrat;
b) ;
în) ;
G)

Ce se mai poate spune despre liniile care se intersectează? Între ele este definit un unghi. Dar luați în considerare formula unghiului universal din următorul paragraf:

Liniile drepte care se intersectează se află în mod necesar în același plan:

Primul gând este să te sprijini pe punctul de intersecție cu toată puterea ta. Și imediat m-am gândit, de ce să-ți refuzi dorințele potrivite?! Să sărim pe ea chiar acum!

Cum să găsiți punctul de intersecție al liniilor spațiale?

Exemplul 14

Aflați punctul de intersecție al dreptelor

Soluţie: Să rescriem ecuațiile liniilor în formă parametrică:

Această sarcină a fost analizată în detaliu în Exemplul nr. 7 al acestei lecții (vezi. Ecuațiile unei linii drepte în spațiu). Și liniile drepte în sine, apropo, am luat-o din Exemplul nr. 12. Nu voi minți, îmi este prea lene să inventez altele noi.

Soluția este standard și a fost deja întâlnită când am elaborat ecuațiile perpendicularei comune a liniilor oblice.

Punctul de intersecție al dreptelor aparține dreptei, prin urmare coordonatele acesteia satisfac ecuațiile parametrice ale acestei drepte și corespund cu o valoare a parametrului foarte specific:

Dar același punct aparține celei de-a doua linii, prin urmare:

Echivalăm ecuațiile corespunzătoare și facem simplificări:

Se obține un sistem de trei ecuații liniare cu două necunoscute. Dacă liniile se intersectează (după cum se dovedește în Exemplul 12), atunci sistemul este în mod necesar consistent și are o soluție unică. Se poate rezolva metoda Gauss, dar nu vom păcătui cu un astfel de fetișism de grădiniță, să o facem mai ușor: din prima ecuație exprimăm „te zero” și îl înlocuim în a doua și a treia ecuație:

Ultimele două ecuații s-au dovedit a fi în esență aceleași și din ele rezultă că . Apoi:

Să substituim valoarea găsită a parametrului în ecuații:

Răspuns:

Pentru a verifica, înlocuim valoarea găsită a parametrului în ecuații:
Au fost obținute aceleași coordonate așa cum se cere pentru a fi verificate. Cititorii meticuloși pot înlocui coordonatele punctului din original ecuații canonice direct.

Apropo, a fost posibil să faceți opusul: găsiți punctul prin „es zero” și verificați-l prin „te zero”.

Un semn matematic binecunoscut spune: acolo unde se discută intersecția liniilor drepte, există întotdeauna un miros de perpendiculare.

Cum se construiește o linie de spațiu perpendiculară pe una dată?

(liniile se intersecteaza)

Exemplul 15

a) Compuneți ecuațiile unei drepte care trece printr-un punct perpendicular pe dreaptă (liniile se intersectează).

b) Aflați distanța de la punct la linie.

Notă : clauza „liniile se intersectează” - esenţial. Prin punct
este posibil să se traseze un număr infinit de drepte perpendiculare care se vor intersecta cu dreapta „el”. Singura decizie are loc în cazul în care punct dat trasat drept, perpendicular Două linii drepte date (vezi Exemplul nr. 13, paragraful „b”).

A) Soluţie: Notați linia necunoscută cu . Să facem un desen schematic:

Ce se știe despre linie? După condiție, se acordă un punct. Pentru a compune ecuațiile unei drepte este necesar să se găsească vectorul direcție. Ca un astfel de vector, vectorul este destul de potrivit și ne vom ocupa de el. Mai precis, să luăm capătul necunoscut al vectorului la strâns.

1) Vom extrage vectorul său de direcție din ecuațiile dreptei „el”, și vom rescrie ecuațiile în sine în formă parametrică:

Mulți au ghicit că acum, pentru a treia oară într-o lecție, magicianul va scoate o lebădă albă din pălărie. Luați în considerare un punct cu coordonate necunoscute. Deoarece punctul , atunci coordonatele sale satisfac ecuațiile parametrice ale dreptei „el” și corespund unei valori specifice parametrului:

Sau într-o singură linie:

2) Prin condiție, liniile trebuie să fie perpendiculare, prin urmare, vectorii lor de direcție sunt ortogonali. Și dacă vectorii sunt ortogonali, atunci lor produs scalar este egal cu zero:

Ce s-a întâmplat? Cea mai simplă ecuație liniară cu o necunoscută:

3) Valoarea parametrului este cunoscută, să găsim punctul:

Și vectorul direcție:
.

4) Vom compune ecuațiile dreptei după punctul și vectorul direcție:

Numitorii proporției s-au dovedit a fi fracționari și exact acesta este cazul când este cazul să scăpăm de fracții. Le voi înmulți doar cu -2:

Răspuns:

Notă : o finalitate mai riguroasă a soluției se întocmește astfel: compunem ecuațiile unei drepte printr-un punct și un vector de direcție . Într-adevăr, dacă un vector este un vector de direcție al unei linii drepte, atunci vectorul coliniar cu acesta, desigur, va fi și un vector de direcție al acestei linii drepte.

Verificarea constă în două etape:

1) verificați vectorii de direcție ai liniilor pentru ortogonalitate;

2) substituim coordonatele punctului în ecuațiile fiecărei linii drepte, acestea ar trebui să se „podă” atât aici, cât și acolo.

S-a vorbit mult despre acțiuni tipice, așa că am făcut o verificare a unui draft.

Apropo, am uitat un alt mod - să construiesc un punct „sue” simetric cu punctul „en” în raport cu linia dreaptă „el”. Cu toate acestea, există un bun „analog plat”, care poate fi găsit în articol Cele mai simple probleme cu o linie dreaptă pe un plan. Aici, toată diferența va fi în coordonatele suplimentare „Z”.

Cum se află distanța de la un punct la o linie în spațiu?

b) Soluţie: Găsiți distanța de la un punct la o linie.

Metoda unu. Aceasta distanta este exact egala cu lungimea perpendicularei: . Soluția este evidentă: dacă se cunosc punctele , apoi:

Metoda a doua. În problemele practice, baza perpendicularei este adesea un mister, așa că este mai rațional să folosiți o formulă gata făcută.

Distanța de la un punct la o linie este exprimată prin formula:
, unde este vectorul de direcție al dreptei „el” și - arbitrar un punct pe o dreaptă dată.

1) Din ecuațiile dreptei obținem vectorul direcție și punctul cel mai accesibil .

2) Punctul este cunoscut din condiția, ascuți vectorul:

3) Să găsim produs vectorial si calculeaza-i lungimea:

4) Calculați lungimea vectorului direcție:

5) Astfel, distanța de la un punct la o dreaptă:

Dispunerea reciprocă a două linii drepte în spațiu.

Dispunerea reciprocă a două linii și spațiu este caracterizată de următoarele trei posibilități.

Dreptele se află în același plan și nu au puncte comune - drepte paralele.

Liniile se află în același plan și au un punct comun - liniile se intersectează.

În spațiu, două linii drepte pot fi încă situate în așa fel încât să nu se afle în același plan. Astfel de linii se numesc intersectare (nu se intersectează și nu sunt paralele).

EXEMPLU:

PROBLEMA 434 Triunghiul ABC se află în plan, a

Triunghiul ABC se află în plan, iar punctul D nu este în acest plan. Punctele M, N și respectiv K, punctele medii ale segmentelor DA, DB și DC

Teorema. Dacă una dintre două drepte se află într-un anumit plan, iar cealaltă intersectează acest plan și un punct care nu se află pe prima linie, atunci aceste linii se intersectează.

Pe fig. 26 linia a se află în plan, iar dreapta c se intersectează în punctul N. Dreptele a și c se intersectează.

Teorema. Prin fiecare dintre cele două drepte care se intersectează trece doar un plan paralel cu cealaltă dreaptă.

Pe fig. 26 de linii a și b se intersectează. Cheren linie dreaptă și plan trasat a (alfa) || b (linia dreaptă a1 || b este indicată în planul B (beta).

Teorema 3.2.

Două drepte paralele cu o a treia sunt paralele.

Această proprietate se numește tranzitivitatea linii paralele.

Dovada

Fie dreptele a și b simultan paralele cu dreapta c. Să presupunem că a nu este paralelă cu b, atunci linia a intersectează linia b într-un punct A care nu se află pe dreapta c prin presupunere. Prin urmare, avem două drepte a și b care trec prin punctul A care nu se află pe dreapta dată c și simultan paralele cu acesta. Acest lucru contrazice Axioma 3.1. Teorema a fost demonstrată.

Teorema 3.3.

Printr-un punct care nu se află pe o dreaptă dată, se poate trasa una și o singură linie paralelă cu dreapta dată.

Dovada

Fie (AB ) o dreaptă dată și C un punct care nu se află pe ea. Linia AC împarte planul în două semiplane. Punctul B se află într-una dintre ele. În conformitate cu axioma 3.2, este posibil să se amâne unghiul de la raza С A (ACD ), egal cu unghiul(CAB), la un alt semiplan. ACD și CAB sunt interioare egale transversal, situate la liniile AB și CD și secantei (AC ) Apoi, în virtutea teoremei 3.1 (AB ) || (CD). Ținând cont de axioma 3.1. Teorema a fost demonstrată.

Proprietatea dreptelor paralele este dată de următoarea teoremă, inversă teoremei 3.1.

Teorema 3.4.

Dacă două drepte paralele sunt intersectate de o a treia linie, atunci unghiurile intersectării sunt egale.

Dovada

Fie (AB ) || (CD). Să presupunem că ACD ≠ BAC . Desenați o dreaptă AE prin punctul A astfel încât EAC = ACD . Dar apoi prin Teorema 3.1 (AE ) || (CD ), iar prin condiție - (AB ) || (CD). Conform teoremei 3.2 (AE ) || (AB). Aceasta contrazice teorema 3.3, conform căreia, printr-un punct A care nu se află pe dreapta CD , se poate trasa o singură dreaptă paralelă cu acesta. Teorema a fost demonstrată.

Figura 3.3.1.

Pe baza acestei teoreme, următoarele proprietăți sunt ușor de fundamentat.

Dacă două drepte paralele sunt intersectate de o a treia linie, atunci unghiurile corespunzătoare sunt egale.

Dacă două drepte paralele sunt intersectate de o a treia linie, atunci suma unghiurilor interioare unilaterale este de 180°.

Corolarul 3.2.

Dacă o dreaptă este perpendiculară pe una dintre drepte paralele, atunci este și perpendiculară pe cealaltă.

Conceptul de paralelism ne permite să introducem următorul concept nou, care va fi necesar mai târziu în capitolul 11.

Cele două grinzi sunt numite în egală măsură dirijat, dacă există o astfel de dreaptă încât, în primul rând, să fie perpendiculare pe această dreaptă și, în al doilea rând, razele se află într-un semiplan în raport cu această dreaptă.

Cele două grinzi sunt numite directii opuse, dacă fiecare dintre ele este în mod egal direcționat cu o rază complementară celeilalte.

Vom nota razele îndreptate egal AB și CD: și razele direcționate opus AB și CD -

Figura 3.3.2.

Semn al liniilor care se intersectează.

Dacă una dintre două linii se află într-un anumit plan, iar cealaltă linie intersectează acest plan într-un punct care nu se află pe prima linie, atunci aceste linii sunt oblice.

Cazuri de aranjare reciprocă a liniilor în spațiu.

1. Există patru cazuri diferite de locație a două linii în spațiu:

   
   

   - intersectarea directă, i.e. nu stați în același plan;

   – liniile se intersectează, adică se află în același plan și au un punct comun;

   - paralelă dreptă, adică se află în același plan și nu se intersectează;

   - liniile coincid.

   
   

   Să obținem semne ale acestor cazuri de aranjare reciprocă a dreptelor date de ecuațiile canonice

   
   
   Unde sunt puncte aparținând liniilorși respectiv, a- vectori de direcţie (Fig. 4.34). Notează prinun vector care leagă punctele date.
   
   

   Cazurile de mai sus de aranjare reciprocă a liniilor corespund următoarelor caracteristici:

   
   

   – vectorii direcți și de încrucișare nu sunt coplanari;

   
   

   – liniile și vectorii de intersectare sunt coplanari, dar vectorii nu sunt coliniari;

   
   

   – vectorii drepti și paraleli sunt coliniari, dar vectorii nu sunt coliniari;

   
   

   sunt drepte și coincid vectorii sunt coliniari.

   
   

   Aceste condiții pot fi scrise folosind proprietățile produselor mixte și vectoriale. Amintiți-vă că produsul mixt al vectorilor din sistemul de coordonate dreptunghiular drept este găsit prin formula:

   
   
   și intersectează determinantul este egal cu zero, iar al doilea și al treilea rând nu sunt proporționale, adică.
   

   - liniile drepte și al doilea și al treilea rând paralel al determinantului sunt proporționale, adică. iar primele două linii nu sunt proporționale, adică.

   
   

   sunt linii drepte și coincid; toate rândurile determinantului sunt proporționale, adică

Dovada criteriului pentru liniile oblice.

Dacă una dintre cele două drepte se află într-un plan, iar cealaltă intersectează acest plan într-un punct care nu aparține primei linii, atunci aceste două linii se intersectează.

Dovada

Fie a aparține lui α, b intersectează α = A, A nu aparține lui a (desenul 2.1.2). Să presupunem că liniile a și b nu se intersectează, adică se intersectează. Atunci există un plan β căruia îi aparțin dreptele a și b. Linia a și punctul A se află în acest plan β. Deoarece linia a și punctul A din afara ei definesc un plan unic, atunci β = α. Dar b conduce β și b nu aparține lui α, deci egalitatea β = α este imposibilă.

Dacă două drepte din spațiu au un punct comun, atunci se spune că aceste două drepte se intersectează. În figura următoare, liniile a și b se intersectează în punctul A. Liniile a și c nu se intersectează.

Oricare două linii fie au un singur punct comun, fie nu au puncte comune.

Linii paralele

Două drepte din spațiu se numesc paralele dacă se află în același plan și nu se intersectează. Pentru a desemna linii paralele utilizați o pictogramă specială - ||.

Notația a||b înseamnă că linia a este paralelă cu dreapta b. În figura de mai sus, liniile a și c sunt paralele.

Teorema liniilor paralele

Prin orice punct din spațiu care nu se află pe o dreaptă dată, trece o dreaptă paralelă cu dreapta dată și, în plus, doar una.

Liniile încrucișate

Două drepte care se află în același plan se pot intersecta sau pot fi paralele. Dar în spațiu, două linii drepte nu trebuie să aparțină aceluiași plan. Ele pot fi amplasate în două planuri diferite.

Evident, liniile situate în planuri diferite nu se intersectează și nu sunt drepte paralele. Se numesc două drepte care nu se află în același plan A întrece măsura.

Figura următoare arată două drepte care se intersectează a și b care se află în planuri diferite.

Semn și teorema liniilor oblice

Dacă una dintre două linii se află într-un anumit plan, iar cealaltă linie intersectează acest plan într-un punct care nu se află pe prima linie, atunci aceste linii sunt oblice.

Teorema liniilor încrucișate: prin fiecare dintre cele două drepte care se intersectează trece un plan paralel cu cealaltă dreaptă și, în plus, doar unul.

Astfel, am luat în considerare toate cazurile posibile de aranjare reciprocă a liniilor în spațiu. Sunt doar trei.

1. Liniile se intersectează. (Adică au un singur punct comun.)

2. Liniile sunt paralele. (Adică nu au puncte comune și se află în același plan.)

3. Liniile drepte se intersectează. (Adică sunt situate în planuri diferite.)