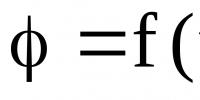Identități și transformări trigonometrice. Toate formulele în trigonometrie Formule pentru reducerea funcțiilor trigonometrice

În trigonometrie, multe formule sunt mai ușor de dedus decât de memorat. Cosinusul unui unghi dublu este o formulă minunată! Vă permite să obțineți formulele de reducere și formulele de jumătate de unghi.

Deci, avem nevoie de cosinusul unghiului dublu și unitatea trigonometrică:

Ele sunt chiar similare: în formula cosinusului unui unghi dublu - diferența dintre pătratele cosinusului și sinusului, iar în unitatea trigonometrică - suma lor. Dacă exprimăm cosinusul din unitatea trigonometrică:

și înlocuiți-l în cosinusul unghiului dublu, obținem:

Aceasta este o altă formulă pentru cosinusul unui unghi dublu:

Această formulă este cheia pentru obținerea formulei de reducere:

Deci, formula pentru scăderea gradului sinusului este:

Dacă în el unghiul alfa este înlocuit cu o jumătate de unghi alfa în jumătate, iar unghiul dublu doi alfa este înlocuit cu unghiul alfa, atunci obținem formula pentru jumătate de unghi pentru sinus:

Acum, din unitatea trigonometrică, exprimăm sinusul:

Înlocuiți această expresie în formula pentru cosinusul unui unghi dublu:

Avem o altă formulă pentru cosinusul unui unghi dublu:

Această formulă este cheia pentru găsirea formulei de reducere a cosinusului și a semiunghiului pentru cosinus.

Astfel, formula pentru scăderea gradului de cosinus este:

Dacă înlocuim α cu α/2 în el și 2α cu α, atunci obținem formula pentru jumătatea argumentului pentru cosinus:

Deoarece tangenta este raportul dintre sinus și cosinus, formula tangentei este:

Cotangenta este raportul dintre cosinus și sinus. Deci formula cotangentei este:

Desigur, în procesul de simplificare a expresiilor trigonometrice, nu are rost să derivăm formule cu jumătate de unghi sau să scădem gradul de fiecare dată. Este mult mai ușor să pui o foaie de formule în fața ta. Și simplificarea va avansa mai repede, iar memoria vizuală se va activa pentru memorare.

Dar tot merită să derivam aceste formule de mai multe ori. Atunci vei fi absolut sigur că în timpul examenului, când nu există nicio modalitate de a folosi o foaie de cheat, le poți obține cu ușurință dacă este nevoie.

Pe această pagină veți găsi toate formulele trigonometrice de bază care vă vor ajuta să rezolvați multe exerciții, simplificând foarte mult expresia în sine.

Formulele trigonometrice sunt egalități matematice pentru funcțiile trigonometrice care sunt valabile pentru toate valorile argumentelor valide.

Formulele stabilesc relația dintre principalele funcții trigonometrice - sinus, cosinus, tangentă, cotangentă.

Sinusul unui unghi este coordonata y a unui punct (ordonata) pe cerc unitar. Cosinusul unui unghi este coordonata x a unui punct (abscisa).

Tangenta și cotangenta sunt, respectiv, raportul dintre sinus și cosinus și invers.
`sin\\alpha,\cos\\alpha`
`tg \ \alpha=\frac(sin\ \alpha)(cos \ \alpha),` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac(cos\ \alpha)(sin\ \alpha),` ` \alpha\ne\pi+\pi n, \ n \in Z`

Și două care sunt folosite mai rar - secante, cosecante. Ele denotă rapoarte de 1 la cosinus și sinus.

`sec \ \alpha=\frac(1)(cos\ \alpha),` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac(1)(sin \ \alpha),` ` \alpha\ne\pi+\pi n,\ n \in Z`

Din definițiile funcțiilor trigonometrice, puteți vedea ce semne au acestea în fiecare trimestru. Semnul funcției depinde doar de cadranul în care se află argumentul.

Când se schimbă semnul argumentului de la „+” la „-”, doar funcția cosinus nu își schimbă valoarea. Se numește chiar. Graficul său este simetric față de axa y.

Funcțiile rămase (sinus, tangentă, cotangentă) sunt impare. Când semnul argumentului este schimbat de la „+” la „-”, valoarea lor se schimbă și în negativă. Graficele lor sunt simetrice față de origine.

`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`

Identități trigonometrice de bază

Identitățile trigonometrice de bază sunt formule care stabilesc o relație între funcțiile trigonometrice ale unui unghi (`sin \ \alpha, \ cos \ \alpha, \ tg \ \alpha, \ ctg \ \alpha`) și care vă permit să găsiți valoarea fiecăreia dintre aceste funcții prin oricare alta cunoscută.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac(\pi n) 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1(cos^2 \alpha)=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1(sin^2 \alpha)=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`

Formule pentru suma și diferența de unghiuri ale funcțiilor trigonometrice

Formulele de adunare și scădere a argumentelor exprimă funcțiile trigonometrice ale sumei sau diferenței a două unghiuri în funcție de funcțiile trigonometrice ale acestor unghiuri.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac(tg \ \alpha+tg \ \beta)(1-tg \ \alpha\ tg \ \beta)`
`tg(\alpha-\beta)=\frac(tg \ \alpha-tg \ \beta)(1+tg \ \alpha \ tg \ \beta)`
`ctg(\alpha+\beta)=\frac(ctg \ \alpha \ ctg \ \beta-1)(ctg \ \beta+ctg \ \alpha)`
`ctg(\alpha-\beta)=\frac(ctg \ \alpha\ ctg \ \beta+1)(ctg \ \beta-ctg \ \alpha)`

Formule cu unghi dublu

`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha) )(1+ctg^2 \alpha)=` `\frac 2(tg \ \alpha+ctg \ \alpha)`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac(1-tg^ 2\alpha)(1+tg^2\alpha)=\frac(ctg^2\alpha-1)(ctg^2\alpha+1)=` `\frac(ctg \ \alpha-tg \ \alpha) (ctg\\alpha+tg\\alpha)`
`tg \ 2\alpha=\frac(2 \ tg \ \alpha)(1-tg^2 \alpha)=` `\frac(2 \ ctg \ \alpha)(ctg^2 \alpha-1)=` `\frac 2( \ ctg \ \alpha-tg \ \alpha)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ ctg \ \alpha)=` `\frac ( \ ctg \ \alpha-tg \ \alpha)2`

Formule cu unghi triplu

`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac(3 \ tg \ \alpha-tg^3 \alpha)(1-3 \ tg^2 \alpha)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \ \alpha)(3 \ ctg^2 \alpha-1)`

Formule cu jumătate de unghi

`sin \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)2)`
`cos \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)2)`
`tg \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)(1+cos \ \alpha))=` `\frac (sin \ \alpha)(1+cos \ \ alpha)=\frac (1-cos \ \alpha)(sin \ \alpha)`
`ctg \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)(1-cos \ \alpha))=` `\frac (sin \ \alpha)(1-cos \ \ alpha)=\frac (1+cos \ \alpha)(sin \ \alpha)`

Formulele cu jumătate, dublu și triplu argument exprimă funcțiile `sin, \cos, \tg, \ctg` ale acestor argumente (`\frac(\alpha)2, \ 2\alpha, \ 3\alpha,… `) în termenii acelorași funcții argument `\alpha`.

Rezultatele lor pot fi obținute din grupul anterior (adunarea și scăderea argumentelor). De exemplu, identitățile cu unghi dublu sunt ușor de obținut prin înlocuirea `\beta` cu `\alpha`.

Formule de reducere

Formulele de pătrate (cuburi etc.) ale funcțiilor trigonometrice vă permit să treceți de la 2,3, ... grade la funcții trigonometrice de gradul întâi, dar unghiuri multiple (`\alpha, \ 3\alpha, \... ` sau `2\alpha, \ 4\alpha, \...`).
`sin^2 \alpha=\frac(1-cos \ 2\alpha)2,` ` (sin^2 \frac \alpha 2=\frac(1-cos \ \alpha)2)`
`cos^2 \alpha=\frac(1+cos \ 2\alpha)2,` ` (cos^2 \frac \alpha 2=\frac(1+cos \ \alpha)2)`
`sin^3 \alpha=\frac(3sin \ \alpha-sin \ 3\alpha)4`
`cos^3 \alpha=\frac(3cos \ \alpha+cos \ 3\alpha)4`
`sin^4 \alpha=\frac(3-4cos \ 2\alpha+cos \ 4\alpha)8`
`cos^4 \alpha=\frac(3+4cos \ 2\alpha+cos \ 4\alpha)8`

Formule pentru suma și diferența funcțiilor trigonometrice

Formulele sunt transformări ale sumei și diferenței funcțiilor trigonometrice ale diferitelor argumente într-un produs.

`sin \ \alpha+sin \ \beta=` `2 \ sin \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2=` `2 \ sin \frac(\alpha+\ beta)2\sin\frac(\beta-\alpha)2`
`tg \ \alpha \pm tg \ \beta=\frac(sin(\alpha \pm \beta))(cos \ \alpha \ cos \ \beta)`
`ctg \ \alpha \pm ctg \ \beta=\frac(sin(\beta \pm \alpha))(sin \ \alpha \ sin \\beta)`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac(cos(\alpha \mp \beta))(cos \ \alpha \ sin \ \beta)`

Aici adunarea și scăderea funcțiilor unui argument sunt convertite într-un produs.

`cos \ \alpha+sin \ \alpha=\sqrt(2) \ cos (\frac(\pi)4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt(2) \sin (\frac(\pi)4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ctg \2\alpha`

Următoarele formule convertesc suma și diferența unei unități și a unei funcții trigonometrice într-un produs.

`1+cos \ \alpha=2 \ cos^2 \frac(\alpha)2`
`1-cos \ \alpha=2 \ sin^2 \frac(\alpha)2`
`1+sin \ \alpha=2 \ cos^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1-sin \ \alpha=2 \ sin^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1 \pm tg \ \alpha=\frac(sin(\frac(\pi)4 \pm \alpha))(cos \frac(\pi)4 \ cos \ \alpha)=` `\frac(\sqrt (2) sin(\frac(\pi)4 \pm \alpha))(cos \ \alpha)`
`1 \pm tg \ \alpha \ tg \ \beta=\frac(cos(\alpha \mp \beta))(cos \ \alpha \ cos \ \beta);` ` \ctg \ \alpha \ ctg \ \ beta \pm 1=\frac(cos(\alpha \mp \beta))(sin \ \alpha \ sin \ \beta)`

Formule de conversie a funcțiilor

Formule pentru conversia produsului funcțiilor trigonometrice cu argumente `\alpha` și `\beta` în suma (diferența) acestor argumente.
`sin \ \alpha \ sin \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(2)`
`sin\alpha \ cos\beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(2)`
`cos \ \alpha \ cos \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(2)`
`tg \ \alpha \ tg \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(cos(\alpha - \beta)+cos(\alpha + \ beta)) =` `\frac(tg \ \alpha + tg \ \beta)(ctg \ \alpha + ctg \ \beta)`
`ctg \ \alpha \ ctg \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(cos(\alpha - \beta)-cos(\alpha + \ beta)) =` `\frac(ctg \ \alpha + ctg \ \beta)(tg \ \alpha + tg \ \beta)`
`tg \ \alpha \ ctg \ \beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(sin(\alpha + \beta)-sin(\alpha - \ beta))`

Substituție trigonometrică universală

Aceste formule exprimă funcții trigonometrice în termenii tangentei unui jumătate de unghi.
`sin \ \alpha= \frac(2tg\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha\ne \pi +2\ pi n, n \in Z`
`cos \ \alpha= \frac(1 - tg^(2)\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha \ ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac(2tg\frac(\alpha)(2))(1 - tg^(2)\frac(\alpha)(2)),` ` \alpha \ne \pi +2\ pi n, n \in Z,` ` \alpha \ne \frac(\pi)(2)+ \pi n, n \in Z`
`ctg \ \alpha = \frac(1 - tg^(2)\frac(\alpha)(2))(2tg\frac(\alpha)(2)),` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`

Formule turnate

Formulele de reducere pot fi obținute folosind astfel de proprietăți ale funcțiilor trigonometrice precum periodicitatea, simetria, proprietatea deplasării cu un unghi dat. Acestea permit convertirea funcțiilor unghiulare arbitrare în funcții al căror unghi este între 0 și 90 de grade.

Pentru unghiul (`\frac (\pi)2 \pm \alpha`) sau (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;`` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
Pentru unghi (`\pi \pm \alpha`) sau (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;`` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;`` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;`` ctg(\pi + \alpha)=ctg \ \alpha`
Pentru unghiul (`\frac (3\pi)2 \pm \alpha`) sau (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 - \alpha)=-cos \ \alpha;`` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 - \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 - \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
Pentru unghi (`2\pi \pm \alpha`) sau (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;`` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;`` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;`` ctg(2\pi + \alpha)=ctg \ \alpha`

Exprimarea unor funcții trigonometrice în termenii altora

`sin \ \alpha=\pm \sqrt(1-cos^2 \alpha)=` `\frac(tg \ \alpha)(\pm \sqrt(1+tg^2 \alpha))=\frac 1( \pm \sqrt(1+ctg^2 \alpha))`
`cos \ \alpha=\pm \sqrt(1-sin^2 \alpha)=` `\frac 1(\pm \sqrt(1+tg^2 \alpha))=\frac (ctg \ \alpha)( \pm \sqrt(1+ctg^2 \alpha))`
`tg \ \alpha=\frac (sin \ \alpha)(\pm \sqrt(1-sin^2 \alpha))=` `\frac (\pm \sqrt(1-cos^2 \alpha))( cos \ \alpha)=\frac 1(ctg \ \alpha)`
`ctg \ \alpha=\frac (\pm \sqrt(1-sin^2 \alpha))(sin \ \alpha)=` `\frac (cos \ \alpha)(\pm \sqrt(1-cos^ 2 \alpha))=\frac 1(tg \ \alpha)`

Trigonometria se traduce literal prin „măsurarea triunghiurilor”. Începe să fie studiat la școală și continuă mai detaliat la universități. Prin urmare, sunt necesare formulele de bază pentru trigonometrie, începând din clasa a X-a, precum și pentru promovarea examenului. Ele denotă conexiuni între funcții și, deoarece există multe dintre aceste conexiuni, există destul de multe formule în sine. A-i aminti pe toate nu este ușor și nu este necesar - dacă este necesar, toate pot fi deduse.

Formulele trigonometrice sunt utilizate în calculul integral, precum și în simplificări, calcule și transformări trigonometrice.

Pentru a rezolva unele probleme, va fi util un tabel de identități trigonometrice, care va face mult mai ușor să faceți transformări ale funcțiilor:

Cele mai simple identități trigonometrice

Coeficientul de împărțire a sinusului unghiului alfa la cosinusul aceluiași unghi este egal cu tangentei acestui unghi (Formula 1). Vezi si dovada corectitudinii transformării celor mai simple identităţi trigonometrice.
Coeficientul de împărțire a cosinusului unghiului alfa la sinusul aceluiași unghi este egal cu cotangentei aceluiași unghi (Formula 2)
Secanta unui unghi este egală cu una împărțită la cosinusul aceluiași unghi (Formula 3)
Suma pătratelor sinusului și cosinusului aceluiași unghi este egală cu unu (Formula 4). Vezi si dovada sumei pătratelor cosinusului și sinusului.
Suma unității și tangentei unghiului este egală cu raportul unității la pătratul cosinusului acestui unghi (Formula 5)
Unitatea plus cotangenta unghiului este egal cu câtul împărțirii unității la pătratul sinus al acestui unghi (Formula 6)
Produsul tangentei și cotangentei aceluiași unghi este egal cu unu (Formula 7).

Conversia unghiurilor negative ale funcțiilor trigonometrice (pare și impare)

Pentru a scăpa de valoarea negativă a gradului de măsură a unghiului la calcularea sinusului, cosinusului sau tangentei, puteți utiliza următoarele transformări trigonometrice (identități) bazate pe principiile funcțiilor trigonometrice pare sau impare.

Așa cum se vede, cosinus iar secanta este chiar funcția , sinus, tangentă și cotangentă sunt funcții impare.

Sinusul unui unghi negativ este egal cu valoarea negativă a sinusului aceluiași unghi pozitiv (minus sinusul alfa).
Cosinusul „minus alfa” va da aceeași valoare ca și cosinusul unghiului alfa.
Tangenta minus alfa este egală cu minus tangenta alfa.

Formule de reducere a unghiului dublu (sinus, cosinus, tangentă și cotangentă a unui unghi dublu)

Dacă trebuie să împărțiți unghiul la jumătate sau invers, treceți de la un unghi dublu la un singur unghi, puteți utiliza următoarele identități trigonometrice:

Conversie cu unghi dublu (unghi dublu sinus, unghi dublu cosinus și unghi dublu tangente) într-unul singur are loc după următoarele reguli:

Sinusul unui unghi dublu este egal cu dublul produsului dintre sinus și cosinus al unui singur unghi

Cosinusul unui unghi dublu este egală cu diferența dintre pătratul cosinusului unui singur unghi și pătratul sinusului acestui unghi

Cosinusul unui unghi dublu egal cu dublul pătratului cosinusului unui singur unghi minus unu

Cosinusul unui unghi dublu este egal cu unu minus pătratul dublu sinus al unui singur unghi

Tangenta cu unghi dublu este egal cu o fracție al cărei numărător este de două ori tangenta unui singur unghi și al cărei numitor este egal cu unu minus tangentei pătratului unui singur unghi.

Cotangentă cu unghi dublu este egal cu o fracție al cărei numărător este pătratul cotangentei unui singur unghi minus unu, iar numitorul este egal cu dublul cotangentei unui singur unghi

Formule universale de substituție trigonometrică

Formulele de conversie de mai jos pot fi utile atunci când trebuie să împărțiți argumentul funcției trigonometrice (sin α, cos α, tg α) la două și să aduceți expresia la valoarea jumătate a unghiului. Din valoarea lui α obținem α/2 .

Aceste formule sunt numite formule ale substituției trigonometrice universale. Valoarea lor constă în faptul că expresia trigonometrică cu ajutorul lor se reduce la expresia tangentei unei jumătăți de unghi, indiferent de funcțiile trigonometrice ( sin cos tg ctg) au fost inițial în expresia. După aceea, ecuația cu tangenta unei jumătăți de unghi este mult mai ușor de rezolvat.

Identități trigonometrice de transformare semiunghi

Următoarele sunt formulele pentru conversia trigonometrică a jumătate din valoarea unui unghi în valoarea sa întreagă.
Valoarea argumentului funcției trigonometrice α/2 se reduce la valoarea argumentului funcției trigonometrice α.

Formule trigonometrice pentru adăugarea unghiurilor

cos (α - β) = cos α cos β + sin α sin β

sin (α + β) = sin α cos β + sin β cos α

sin (α - β) = sin α cos β - sin β cos α
cos (α + β) = cos α cos β - sin α sin β

Tangenta și cotangenta sumei unghiurilor alfa și beta pot fi convertite în conformitate cu următoarele reguli pentru conversia funcțiilor trigonometrice:

Tangenta sumei unghiurilor este egal cu o fracție al cărei numărător este suma tangentei primului unghi și tangentei celui de-al doilea unghi, iar numitorul este unu minus produsul tangentei primului unghi și tangentei celui de-al doilea unghi.

Diferența de unghi tangentă este egal cu o fracție, al cărei numărător este egal cu diferența dintre tangentei unghiului redus și tangentei unghiului de scăzut, iar numitorul este unu plus produsul tangentelor acestor unghiuri.

Cotangenta sumei unghiurilor este egal cu o fracție al cărei numărător este egal cu produsul cotangentelor acestor unghiuri plus unu, iar numitorul este egal cu diferența dintre cotangentei celui de-al doilea unghi și cotangentei primului unghi.

Cotangente a diferenței de unghi este egal cu o fracție al cărei numărător este produsul dintre cotangentele acestor unghiuri minus unu și numitorul este egală cu suma cotangente ale acestor unghiuri.

Aceste identități trigonometrice sunt convenabile de utilizat atunci când trebuie să calculați, de exemplu, tangenta de 105 grade (tg 105). Dacă este reprezentat ca tg (45 + 60), atunci puteți utiliza transformările identice date ale tangentei sumei unghiurilor, după care pur și simplu înlocuiți valorile tabelare. tangenta 45și tangenta 60 grade.

Formule pentru conversia sumei sau diferențelor funcțiilor trigonometrice

Expresiile reprezentând suma formei sin α + sin β pot fi convertite folosind următoarele formule:

Formule cu unghi triplu - convertiți sin3α cos3α tg3α în sinα cosα tgα

Uneori este necesar să convertiți valoarea triplă a unghiului astfel încât unghiul α să devină argumentul funcției trigonometrice în loc de 3α.
În acest caz, puteți utiliza formulele (identitățile) pentru transformarea unghiului triplu:

Formule pentru transformarea produsului funcțiilor trigonometrice

Dacă devine necesar să convertiți produsul sinusurilor diferitelor unghiuri ale cosinusurilor diferitelor unghiuri sau chiar produsul dintre sinus și cosinus, atunci puteți utiliza următoarele identități trigonometrice:


În acest caz, produsul funcțiilor sinus, cosinus sau tangentă ale diferitelor unghiuri va fi convertit într-o sumă sau diferență.

Formule de reducere a funcţiilor trigonometrice

Trebuie să utilizați tabelul de distribuție după cum urmează. În linie, selectați funcția care ne interesează. Coloana este un unghi. De exemplu, sinusul unghiului (α+90) la intersecția primului rând și a primei coloane, aflăm că sin (α+90) = cos α .